3.4 ルーティング
ここまで本章では、スイッチとルーターがネットワークトポロジーに関する十分な知識を持っており、受け取ったパケットをどのポートから送信すべきかを正しく選択できることを仮定してきた。仮想回線では、ルーティングは接続要求パケットだけで必要になる: それ以降のパケットは接続要求パケットと同じ経路を利用する。IP ネットワークを含むデータグラムネットワークでは、全てのパケットでルーティングが必要になる。いずれの場合でも、スイッチおよびルーターは宛先アドレスを見てそのアドレスにパケットを運ぶために最も適した出力ポートを選択できなくてはならない。ルーティングにおける基礎的な問題は「スイッチとルーターが転送テーブルの情報をどのように収集するか」である。
教訓
転送 (forwarding) とルーティング (routing) の重要な (しかし見過ごされることの多い) 違いを繰り返しておく。転送はパケットを受け取り、宛先アドレスを使ってテーブルからエントリーを取得し、そのエントリーに記された方向にパケットを送信する処理を指す。これは各ノードでローカルに行われる単純で曖昧さの無いプロセスであり、ネットワークのデータプレーン (data plane) と呼ばれる。これに対してルーティングは転送テーブルを構築する処理を指す。ルーティングは複雑な分散アルゴリズムが関係し、ネットワークのコントロールプレーン (control plane) と呼ばれる。
転送テーブル (forwarding table) とルーティングテーブル (routing table) が交換可能な語として使われる場合もあるが、本書では区別して使う。転送テーブルはパケットが転送されるときに使われるテーブルであり、転送の処理に必要な情報を全て含む。これは、転送テーブルの各行がネットワークプレフィックスから外向きのインターフェース番号および何らかの MAC 情報 (例えばネクストホップのイーサネットアドレス) への対応付けであることを意味する。これに対してルーティングテーブルはルーティングアルゴリズムによって構築されるテーブルであり、転送テーブルよりも前に構築される。ルーティングテーブルには通常ネットワークプレフィックスからネクストホップへの対応付けが含まれる。他にも、ルーターがその対応付けを破棄するタイミングを判断するために、情報の入手経路に関する情報が含まれる場合もある。
ルーティングテーブルと転送テーブルを異なるデータ構造とするかどうかは実装が自由に決められるものの、別のデータ構造とするべき理由が多く存在する。例えば、転送テーブルはパケットの転送で行われる宛先アドレスを使った検索が高速になるように最適化する必要がある。これに対して、ルーティングテーブルはネットワークトポロジーが変化したときの再計算が簡単に行えるように最適化する必要がある。多くの場合で転送テーブルは専用ハードウェアで実装されるが、ルーティングテーブルが専用ハードウェアで実装されることはまずない。
表 14 にルーティングテーブルの行の例を示す。ネットワークプレフィックス 18/8 に到達するには IP アドレス 171.69.245.10 のルーターをネクストホップとするべきであることが示されている。
| プレフィックス/長さ | ネクストホップ |
|---|---|
18/8 |
171.69.245.10 |
これに対して、表 15 に示したのは転送テーブルの行の例である。ここにはパケットをネクストホップに転送するには何をすべきかが具体的に示されている: この行は「ネットワーク 18/8 に宛てられたパケットを受け取ったら、MAC アドレス 8:0:2b:e4:b:1:2 を宛先としてインターフェース番号 0 からそのパケットを送信せよ」と読める。なお、MAC アドレスに関する情報は ARP によって提供される。
| プレフィックス/長さ | インターフェース番号 | MAC アドレス |
|---|---|---|
18/8 |
if0 | 8:0:2b:e4:b:1:2 |
ルーティングテーブルの詳細に入る前に、インターネットで用いられる仕組みを作るときに必ず考えなくてはならない質問を思い出しておく必要がある: 「その解決策はスケールするか?」である。 本節で説明されるアルゴリズムとプロトコルに関して言うと、どれも中規模 ── 数百ノード ── のネットワークで使われるものとして設計されているので、その答えは「あまりスケールしない」となる。しかし、本節で見る解決策は現在のインターネットで用いられる階層的ルーティングインフラストラクチャの構成要素としては確かに利用される。具体的に言うと、これから説明するプロトコルは総称してドメイン内 (intradomain) ルーティングプロトコル、あるいは IGP (Interior Gateway Protocol, 内部ゲートウェイプロトコル) と呼ばれる。これらの用語を理解するには、ルーティングにおけるドメイン (domain) を理解する必要がある。とりあえずは、全てのルーターが同一の管理制御下にあるインターネットワーク (例えば単一の大学のキャンパスに敷設されたネットワーク、あるいは単一の ISP が提供するネットワーク) をドメインと呼ぶと考えておけば問題無い。この定義の妥当性は次章でドメイン間 (interdomain) ルーティングプロトコルを見ていくときに明らかになる。ともかく、本節では小規模から中規模のネットワークにおけるルーティングの問題を考えるのだと頭に入れておいてほしい。インターネットのようなサイズのネットワークのルーティングではない。
3.4.1 グラフとしてのネットワーク
ルーティングは本質的にグラフ理論の問題である。図 84 にネットワークのグラフ表現の例を示す。このグラフの頂点 (A から F のラベルが付いた円) はホストかもしれないし、スイッチ、ルーター、ネットワークかもしれない。最初はグラフの頂点がルーターだとして議論を進める。このときグラフの辺はネットワークのリンクに対応する。それぞれの辺はコスト (cost) を持ち、そのリンクを通じたトラフィックの送信がどれだけ行われるべきかがコストによって示される。辺に対するコストの割り当てに関する議論は第 3.4.4 項で行う。
これから本節では図 84 のネットワーク (グラフ) を例として使っていく。このグラフは単一のコストが割り当てられた無向の辺を持っているが、これは小さな単純化と言えることに注意してほしい。辺を有向にして、接続されているノードの間に両方向の辺を張ってそれぞれの方向でコストが異なるようにした方が正確になる。
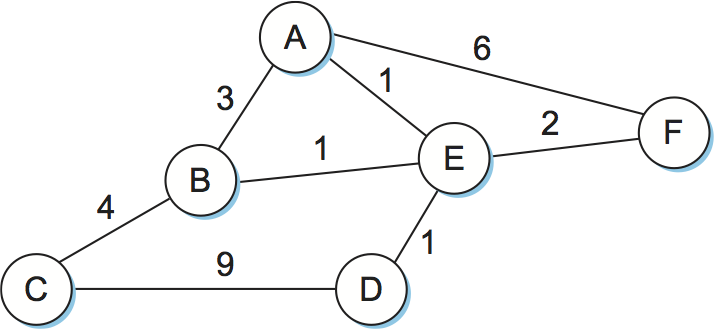
ルーティングにおける基礎的な問題は、任意の頂点の組に対してそれらを結ぶ路の中でコストが最小のもの (最小コスト路) を見つける問題である。ここで路のコストは路に含まれる辺のコストの和に等しい。図 84 のような単純なネットワークでは、全ての最小コスト路を計算して各ノードの不揮発性ストレージに保存しておく方法が考えられる。そういった静的なアプローチにはいくつか欠点がある:
-
ノードやリンクの障害に対応できない。
-
ノードやリンクの追加に対応できない。
-
辺のコストを変更できない。負荷の高いリンクのコストを上げるなど、辺のコストを変更するシナリオは当然考えられる。
こういった理由により、最も実践的なネットワークにおいてルーティングはルーティングプロトコルをノード間で実行することで達成される。こういったプロトコルはリンクとノードで障害やコストの変更がある状況で最小コスト路を見つける問題を分散された形で動的に解く手段を提供する。一つ前の文で使った「分散」という言葉に注目してほしい: 中央集権的なアルゴリズムはスケールさせるのが難しいので、広く使われているルーティングプロトコルはどれも分散アルゴリズムを利用している。
分散アルゴリズムを必要とすることが理由の一つとなって、ルーティングプロトコルの研究と開発は活発に行われている ── 分散アルゴリズムを効率良く動作させるための課題は数多く存在する。例えば、分散アルゴリズムを使うと二つのルーターが考える最小コスト路が一致しなくなる可能性が生じる: 隣り合うルーターがお互いを最小コスト路の一部だと思ってパケットを送り合う状況が生じるようになる。そうなると二つのルーター間の矛盾が解消されるまでパケットは無限にループし続けるので、可能な限り早く矛盾を解消する必要がある。これはルーティングプロトコルが解決しなければならない問題の一種に過ぎない。
本書では距離ベクトル型ルーティング (distance vector routing) とリンク状態型ルーティング (link state routing) という古典的な二つのルーティングアルゴリズムを紹介する。距離ベクトル型ルーティングは考案者の名前を取ってベルマン-フォード型ルーティング (Bellman-Ford routing) と呼ばれることもある。本節ではネットワークの辺のコストは既知だと仮定し、辺のコストを意味のある形で計算する問題は第 3.4.4 項で触れる。
3.4.2 距離ベクトル型ルーティング (RIP)
距離ベクトル型ルーティングの裏にあるアイデアはその名前が示している: 各頂点は全てのノードとの "距離" (コスト) が記された一次元配列 (ベクトル) を構築し、それを隣接するノードに配布する。距離ベクトル型ルーティングは「各ノードは自身と隣接するノードの間のコストを知っている」という事実を帰納法のベースケースの仮定として利用する。そのコストは例えばネットワーク管理者がルーターを設定するときに割り当てられたのかもしれない。なお、ダウンしているリンクには無限のコストが割り当てられる。
| A | B | C | D | E | F | G | |
|---|---|---|---|---|---|---|---|
| A | 0 | 1 | 1 | ∞ | 1 | 1 | ∞ |
| B | 1 | 0 | 1 | ∞ | ∞ | ∞ | ∞ |
| C | 1 | 1 | 0 | 1 | ∞ | ∞ | ∞ |
| D | ∞ | ∞ | 1 | 0 | ∞ | ∞ | 1 |
| E | 1 | ∞ | ∞ | ∞ | 0 | ∞ | ∞ |
| F | 1 | ∞ | ∞ | ∞ | ∞ | 0 | 1 |
| G | ∞ | ∞ | ∞ | 1 | ∞ | 1 | 0 |
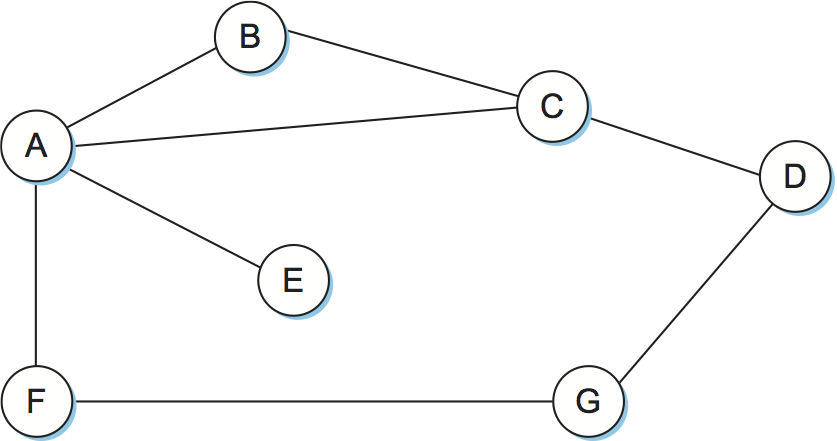
図 85 の例を使って距離ベクトル型ルーティングの動作を説明しよう。ここではリンクのコストは全て 1 とする (リンクのコストが全て同じなので、図では省略してある)。このとき最小コスト路はホップの最も少ない路となる。各ノードが持っている他の全てのノードへの距離に関する知識は表 16 のようにまとめられる。各ノードは自分の名前が左端に書かれた一行しか知らないことに注意してほしい。グローバルな視点で表全体を見渡せるのは我々だけであり、ネットワーク内のノードは自身の行しか見ることができない。
表 16 の各行は左端に記されたノードが自身と他のノードとの距離と現在信じている値を表していると考えられる。最初、各ノードは自身と隣接するノードとの距離を 1 に設定し、それ以外のノードとの距離を ∞ に設定する。例えば A は最初「B には 1 ホップで到達可能で、D には到達できない」と信じている。A のルーティングテーブルには A が信じていることが記録され、表 17 のようになる。
| 宛先 | コスト | ネクストホップ |
|---|---|---|
| B | 1 | B |
| C | 1 | C |
| D | ∞ | — |
| E | 1 | E |
| F | 1 | F |
| G | ∞ | — |
距離ベクトル型ルーティングテーブルの次のステップでは、全てのノードが自身の信じる距離のベクトルを入れたメッセージを隣接するノードに送信する。例えばノード F はノード A に「自分 (F) は G にコスト 1 で到達できる」と伝える。A は自身がコスト 1 で F に到達できることを知っているので、F が送った情報から自分は F を経由すれば G にコスト 2 で到達できることを学習する。同様に、A は C からの情報および最初に学習した C への到達可能性から、C を経由すればコスト 2 で D に到達できると学習する。この二つの場合では新しく計算されたコストが元々のコスト (無限大) より小さいので、A は距離ベクトルを更新する。同様に、A は C から B にコスト 1 で到達できるという情報を C から受け取り、自身の持つ情報から C を経由すると B にコスト 2 で到達できると認識する。しかしこの場合は元々のコスト (1) の方が小さいので、距離ベクトルは更新されず、新しい情報は破棄される。この時点で A のルーティングテーブルにはネットワーク内の全てのノードに対するコストとネクストホップが記載される。A の最終的なルーティングテーブルを表 18 に示す。
| 宛先 | コスト | ネクストホップ |
|---|---|---|
| B | 1 | B |
| C | 1 | C |
| D | 2 | C |
| E | 1 | E |
| F | 1 | F |
| G | 2 | F |
ネットワークトポロジーが変化しなければ、距離ベクトルを含んだメッセージを隣接ノードと数回やり取りするだけで各ノードは完全なルーティングテーブルを構築できる。全てのノードが一貫したルーティング情報を保持したとき、ルーティングは収束 (convergence) したと言う。図 85 のネットワークでルーティングが収束すると、各ノードから他の全てのノードへの最終的なコストは表 19 のようになる。この表にある全ての情報を持つノードはネットワーク内に存在しない事実はもう一度強調しなければならない ── 各ノードは自身のルーティングテーブルにある情報だけを持つ。中央権威が存在しないにもかかわらず全てのノードが一貫したネットワークの解釈を持てることがこういった分散アルゴリズムの長所である。
| A | B | C | D | E | F | G | |
|---|---|---|---|---|---|---|---|
| A | 0 | 1 | 1 | 2 | 1 | 1 | 2 |
| B | 1 | 0 | 1 | 2 | 2 | 2 | 3 |
| C | 1 | 1 | 0 | 1 | 2 | 2 | 2 |
| D | 2 | 2 | 1 | 0 | 3 | 2 | 1 |
| E | 1 | 2 | 2 | 3 | 0 | 2 | 3 |
| F | 1 | 2 | 2 | 2 | 2 | 0 | 1 |
| G | 2 | 3 | 2 | 1 | 3 | 1 | 0 |
距離ベクトル型ルーティングの議論を終える前に、いくつか指摘しておきたい詳細がある。まず、ノードがルーティング情報の更新を隣接ノードに送る状況は二つある。一つは定期的に送信されるレギュラーアップデート (regular update) であり、各ノードは距離ベクトルに変化が無くても自動的に更新メッセージを送信する。これは他のノードに自分が動いていることを知らせる役割がある。また、現在利用されている経路が使えなくなったときに定期的なメッセージによって必要な情報がもたらされる場合もある。レギュラーアップデートの頻度はプロトコルによって様々だが、典型的には数秒から数分程度である。もう一つはトリガーアップデート (triggered udpate) であり、ノードがリンクの障害を検知したとき、あるいは隣接するノードからの情報で自身のルーティングテーブルが書き換えたときに送信される。ノードはルーティングテーブルが変化すると必ず隣接するノードに更新を送信する。それを受けて隣接するノードでルーティングテーブルの更新が起こったなら、そのノードも隣接するノードに更新を送信する。
続いてリンクあるいはノードで障害が起きたときに何が起こるかを考えよう。そういった場合は障害に最初に気が付いたノードが新しい距離ベクトルを隣接ノードへ送信し、システムは新しい状態に通常すぐに収束する。「ノードはどうやって障害を検出するのか?」という疑問に対する答えはいくつかある。定期的に制御パケットを送って確認応答が返ってくるかどうかを確認することで他のノードへのリンクをチェックするアプローチもあれば、レギュラーアップデートが届かないことが数回続いたらリンク (あるいはリンクの向こう側のノード) で障害が起きていると判断するアプローチもある。
リンク障害を検出したノードで何が起こるかを理解するために、図 85 のネットワークで F が自身と G を結ぶリンクで障害が起きたことを検出したと仮定しよう。このとき F は G への距離を無限大に更新し、その情報を A に送信する。A は G に至るコスト 2 の経路が F を通ることを知っているから、A も G への距離を無限大に設定する。しかし次の C からの更新において、C が G に至るコスト 2 の経路を持っていることを A は知る。そこで A は C を経由すれば G にコスト 3 で到達できることを学習し、3 は無限大より小さいのでルーティングテーブルをそのように更新する。この情報が A から F に伝わったとき、F は A を通れば G にコスト 4 で到達できることを学習する。4 は無限大より小さいから、F もルーティングテーブルを更新する。こうしてシステムは再び安定な状態となる。
しかし残念ながら、状況が少し違うとネットワークが安定しない可能性がある。例えば A と E を結ぶリンクで障害が起きたとしよう。次のレギュラーアップデートで A は E への距離が無限大という情報を広報する (トリガーアップデートは存在しないとしよう) が、それと同時に B と C は E への距離が 2 という情報を送信する。イベントのタイミングが噛み合うと、次のシナリオが発生する可能性がある: C から「E には 2 ホップで到達できる」という情報を受けっとったノード B は、自身は E に 3 ホップで到達できると学習し、その情報を A に送信する。この情報を受け取った A は自身が E に 4 ホップで到達できると学習し、その情報を C に送る。C は以前に A から受け取った情報から E には到達できないと学習しているので、A からの「E には 4 ホップで到達できる」という情報を元に自身は E に 5 ホップで到達できると学習し、以下同様となる。このループは距離が無限大とみなせるほど大きい値になるまで続くので、どのノードも本当は E が到達不可能だと学習できず、ルーティングテーブルが安定しない。この状況は無限数え上げ問題 (count to infinity problem) と呼ばれる。
この問題に対する部分的な解決策がいくつか存在する。第一に、比較的小さな値を無限大の近似値として用いる方法がある。例えば特定のネットワークでパケットが 16 回以上ホップすることはないと確信できるなら、無限大を表す値として 16 を採用できる。こうすれば少なくとも無限大まで数え上げるまでの時間が短縮される。しかし当然、このままだとネットワークが大きくなって 16 ホップ以上離れるノードが出現したときに問題が起きる。
ルーティングを安定化されるまでの時間を短縮するもう一つの方法として、スプリットホライズン (split horizon) と呼ばれる手法がある。そのアイデアは「ノードがルーティング情報の更新を隣接ノードに送るとき、宛先のノードから学んだ経路を送信しない」というものである。例えば図 85 においてノード B のルーティングテーブルに (E, 2, A) というエントリーが含まれるなら、このエントリーが表す経路は A を通る。そのため、B はこのエントリーを省いた更新を A に送信する。
スプリットホライズンをさらに強力にするテクニックにポイズンリバース (poison reverse) がある。先ほどの例でポイズンリバースが有効だと、B は E に向かう経路情報 (A から学んだもの) を A に送り返す。ただしそのとき、B は「B を通って E に到達しようとするな」という情報、例えば (E, ∞) を A に送る。
両方のテクニックに共通する問題として、二つのノードが関係するルーティングループにしか対処できないことがある。三つ以上のノードが関係するルーティングループでは、より抜本的な対策が必要になる。先ほどの例をもう一度考えると、もし B と C が「E とのリンクで障害が起きた」という情報を A から受け取った後に少し待っていれば、両ノードは自身が E に到達できない正しく学習できていただろう。しかし残念ながら、このアプローチだとプロトコルの収束が遅くなる。収束の速さは本節の後半で解説されるリンク状態ルーティングが特に優れる点の一つである。
実装
以上のアルゴリズムを実装するコードは簡単に書ける。基本的なコードをここに示しておく。次の Route 構造体はルーティングテーブルのエントリーを表し、定数 MAX_TTL はルーティングテーブルのエントリーが破棄されるまでの時間を表す。
#define MAX_ROUTES 128 /* ルーティングテーブルの最大サイズ */
#define MAX_TTL 120 /* エントリーが削除されるまでの時間 (秒) */
typedef struct {
NodeAddr Destination; /* 宛先のアドレス */
NodeAddr NextHop; /* ネクストホップのアドレス */
int Cost; /* Destination のコスト */
u_short TTL; /* 生存期間 */
} Route;
int numRoutes = 0;
Route routingTable[MAX_ROUTES];
次の mergeRoute 関数は受け取った新しい経路に基づいてローカルノードのルーティングテーブルを更新する。ここには示されていないが、ノードのルーティングテーブルが持つ経路のリストを定期的にスキャンし、各経路の TTL (time to live, 生存期間) フィールドを減らし、生存期間が 0 になった経路を破棄するタイマー関数が外部で実行されている。ただし、隣接ノードからの更新メッセージによって経路が再度確認されたたときに TTL フィールドが MAX_TTL にリセットされる点に注意してほしい。
void mergeRoute (Route *new) {
int i;
for (i = 0; i < numRoutes; ++i) {
if (new->Destination == routingTable[i].Destination) {
if (new->Cost + 1 < routingTable[i].Cost) {
/* new は現在の記録されているものより優れた経路である */
break;
} else if (new->NextHop == routingTable[i].NextHop) {
/* 現在のネクストホップに対するコストが変わった可能性がある */
break;
} else {
/* new は新しい情報を含んでいない --- 無視する */
return;
}
}
}
if (i == numRoutes) {
/* new は新しい経路である */
/* 記録するための空き容量はあるか? */
if (numRoutes < MAXROUTES) {
++numRoutes;
} else {
/* この経路はルーティングテーブルに収まらないので、諦める */
return;
}
}
routingTable[i] = *new;
/* TTL をリセットする */
routingTable[i].TTL = MAX_TTL;
/* 次のノードに行くまでのホップを加える */
++routingTable[i].Cost;
}
最後に、updateRoutingTable 関数が隣接ノードから受け取った経路更新に含まれる経路のそれぞれに対して mergeRoute を呼び出す。
void updateRoutingTable (Route *newRoute, int numNewRoutes) {
for (int i=0; i < numNewRoutes; ++i) {
mergeRoute(&newRoute[i]);
}
}
RIP (Routing Information Protocol)
IP ネットワークで最も広く使われるルーティングプロトコルの一つに RIP (Routing Information Protocol) がある。IP が生まれたころに RIP が広く使われたのは、様々な商用 Unix の派生元となった BSD (Berkeley Software Distribution) バージョンの Unix と一緒に RIP が配布されたことも関係している。RIP は非常に単純であり、ここまでに説明した距離ベクトルを用いるアルゴリズムの最も有名な例である。
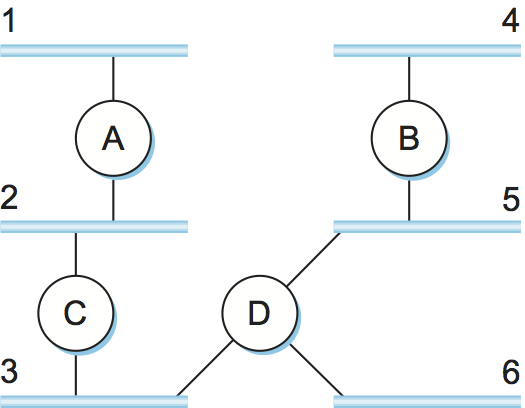
インターネットワークにおけるルーティングプロトコルは本節で説明した理想的なグラフモデルと少しだけ異なる。インターネットワークにおいて、ルーターは様々なネットワークに宛てられたパケットを転送することを目標とする。そのため各ルーターは他のルーターに到達するためのコストを広報するのではなく、ネットワークに到達するためのコストを広報する。例えば図 86 では、ルーター C はルーター A に「自分はネットワーク 2 と 3 (自身が直接接続するネットワーク) にコスト 0 で、ネットワーク 5 と 6 にコスト 1 で、ネットワーク 4 にコスト 2 で到達できる」と広報する。

この事実は図 87 に示した RIP Version 2 (RIPv2) のパケットフォーマットからも確認できる。パケットの大部分は (アドレス, マスク, 距離) の三つ組で占められている。しかし、ルーティングアルゴリズムの基本的な考え方は変わらない。例えばルーター A が「ネットワーク X に到達するには、現在ルーティングテーブルに記されたネクストホップよりも B を通った方が少ないホップで済む」と学習したなら、A はネットワーク X に対するコストとネクストホップの情報を適切に更新する。
RIP は距離ベクトル型ルーティングを非常に忠実に実装する。RIP を実行するルーターは 30 秒ごとに更新 (レギュラーアップデート) を送信し、他のルーターからの更新によって自身のルーティングテーブルが変更されたときも更新 (トリガーアップデート) を送信する。一つ興味深い点として、RIP は IP だけではなく複数のアドレスファミリーをサポートする ── パケットに Family フィールドが存在するのはこのためである。前節で説明したサブネットマスクが導入されたのは RIPv2 であり、RIP Version 1 ではクラスを用いる古い IP アドレスにしか対応していない。
これから見るように、ルーティングプロトコルではリンクに対するメトリック (コスト) として使える値が数多く存在する。RIP は最も単純なアプローチを採用し、全てのリンクのコストを 1 とする (前述した例と同様となる)。そのため、RIP は必ずホップの回数が最小となる経路を探そうとする。正当な距離は 1 から 15 までと決まっており、16 は無限大を表す。このため RIP は比較的小さい ── 任意のノード同士が 16 ホップ以上離れていない ── ネットワークでのみ実行できる。
3.4.3 リンク状態型ルーティング (OSPF)
リンク状態型ルーティング (link-state routing)は二番目に有名なドメイン内ルーティングプロトコルである。この方式は距離ベクトル型ルーティングと同様の仮定を置く: 各ノードは隣接するノードを結ぶリンクの状態 (動作しているかどうか) を確認でき、そのコストを知っていることが仮定される。また、各ノードが任意の宛先に対する最小コスト路が見つけられるだけの情報を与えることが目標となる点も変わらない。
リンク状態型ルーティングのアイデアは非常に単純で、「全てのノードは隣接するノードに到達する方法を知っている。それなら、各ノードが持つ知識を全てのノードに広めれば、全てのノードがネットワークの完全な地図を構築できる」というものである。ネットワーク全体の地図は明らかにネットワークの任意の点への最小コスト路を見つけるために (おそらく必要最小限ではないものの) 十分な情報を持つ。そのため、リンク状態型ルーティングを用いるプロトコルには二つの仕組みが存在する: リンク状態に関する情報の確実な配布と、集まったリンク状態を使った経路の計算である。
確実なフラッディング
確実なフラッディング (reliable flooding) とは、ルーティングプロトコルに参加する全てのノードが他の全てのノードからリンク状態に関する情報を受け取ることを保証するプロセスを言う。フラッディングという言葉が示すように、各ノードが自身に直接接続する全てのリンクにリンク状態に関する情報を送るというのが基本的なアイデアとなる。この情報を受け取った各ノードは、それを自身に直接接続されるリンクの全てに転送する。このプロセスは情報がネットワーク上の全てのノードに行き渡るまで繰り返される。
各ノードは LSP (link-state pakcet, リンク状態パケット) と呼ばれる更新パケットを作成する。正確に言うと、LSP には次の情報が含まれる:
-
この LSP を作成したノードの識別子
-
この LSP を作成したノードに直接接続されている隣接ノードのリスト。加えて、この LSP を作成したノードと隣接ノードを結ぶ各リンクのコスト。
-
シーケンス番号
-
この LSP の生存期間 (time to live)
最初の二つの要素は経路の計算で用いられ、最後の二つの要素はパケットを全てのノードに届ける (フラッディング) 処理を確実に行うために存在する。あるノードに関する矛盾する複数の LSP がネットワーク内に同時に存在する可能性もあるので、「確実なフラッディング」には情報の最新のコピーを届けることも含まれる。フラッディングを確実に行うのは非常に難しいことが歴史から示されている (例えば、ARPANET で用いられた初期のリンク状態型ルーティングは 1981 年にネットワーク障害を起こしている1)。
フラッディングは次のように動作する。まず、隣接ノードに向けた LSP の転送では (リンク層プロトコルと同様に) 確認応答と再送を用いて確実性を保証する。しかし、ネットワーク上の全てのノードに対して LSP を確実にフラッディングするには追加のステップがさらにいくつか必要になる。
ノード X が自分と異なるノード Y によって作成された LSP のコピーを受け取ったとする。Y は X と同じルーティングドメインに属する X でない任意のルーターである可能性がある。X は Y からの LSP のコピーが既に保存されていないかどうかを確認する。もしコピーが存在するなら、X はシーケンス番号を比較する: もし受け取った LSP のシーケンス番号が保存された LSP のシーケンス番号より大きければ、受け取った LSP は保存された LSP より新しいということなので、X は受け取った LSP を保存する (元々の LSP と置き換わる)。受け取った LSP が保存された LSP と同じかそれ未満のシーケンス番号を持つ場合、受け取った LSP は保存された LSP より新しくないということなので、X は受け取った LSP を破棄して処理を終える。新しい LSP を保存した場合、X はその LSP を送ってきたノードを除く全ての隣接ノードにその LSP のコピーを送信する。LSP を送ってきたノードに送り返さない約束はフラッディングの終了を早めるために存在する。X から LSP を受け取った隣接ノードでも同様の処理が起こるので、直近の LSP のコピーはいずれ全てのノードに行き渡る。
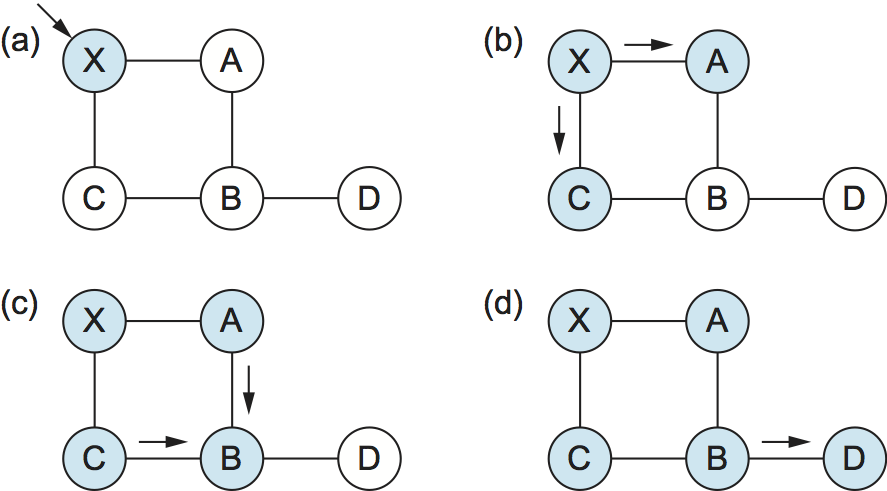
図 88 に小規模なネットワークにおける LSP のフラッディングの例を示す。新しい LSP を保存したノードが水色で示されている。最初 LSP はノード X に到着し (a)、X は隣接する A と C に LSP を送る (b)。A と C は LSP を送ってきたノード X には LSP を送り返さず、B だけに送る (c)。B は同一の LSP を A と C から受け取るので、最初に到着した方を保存し、後に到着した方を破棄する。その後 B は LSP を D に送信する。D は LSP を送信すべき隣接ノードを持たないので、フラッディングはここで完了する。
距離ベクトル型ルーティングと同じように、リンク状態型ルーティングで各ノードは二つの状況下で自発的に LSP を生成する: 一定時間が経過したときと、トポロジーの変化を検出したときである。ただし、ノードが検出するトポロジーの変化は自身に直接接続されたリンクあるいは隣接ノードの障害に限られる。リンクの障害はリンク層プロトコルによって検出できる: 隣接ノードの喪失や接続性の損失は定期的な「Hello パケット」の送信によって検出される。各ノードは設定された時間が経過するごとに隣接ノードへ Hello パケットを送信する。十分長く待っても Hello パケットが返ってこない隣接ノードがあれば、そのノードと自身を結ぶリンクで障害が起きたと判断され、この状況を反映する新しい LSP が生成される。
リンク状態型ルーティングを用いるプロトコルのフラッディングメカニズムで最も重要な設計目標は、最新の情報を可能な限り早く全てのノードに行き渡らせ、それと同時に古い情報を確実にネットワークから取り除いて送信されないようにすることである。加えて、ルーティング処理でネットワークに送信されるトラフィックの総量が小さいことが当然望ましい: ネットワークをアプリケーションのために利用するユーザーから見れば、ルーティングに使われるトラフィックは結局オーバーヘッドに過ぎない。こういった目標を達成するための手法をこれからの数段落で説明する。
オーバーヘッドを削減する簡単な方法の一つとして「本当に必要でなければ LSP を生成しない」がある。これは定期的な LSP 生成の間隔を非常に長くすることで行える ── 数時間のオーダーであることも珍しくない。トポロジーが変わったときにフラッディングプロトコルが本当に確実に動作すると確信できるなら、「変化無し」と伝えるメッセージを送る頻度は低くても構わない。
古い情報が新しい情報で確実に置き換えられるように、LSP はシーケンス番号を持っている。新しい LSP を生成するとき、ノードは毎回シーケンス番号を 1 増加させる。様々なプロトコルで用いられるシーケンス番号とは異なり、LSP のシーケンス番号は最大値の後に 0 に戻る (ラップアラウンドする) とルーティングアルゴリズムが機能しなくなる。そのためシーケンス番号を収めるフィールドは非常に長く (例えば 64 ビットが) 確保される。障害が起こっていたノードがネットワークに復帰すると、シーケンス番号は 0 にリセットされる。障害が長かったなら、古い LSP はタイムアウト (後述) によってネットワークから消えている。障害が短かったなら、障害から復帰したノードはいずれ自身がかつて送信した LSP のコピーを受け取る。その LSP は 0 より大きなシーケンス番号を持っているはずだから、復帰したノードは自身のシーケンス番号をその値に 1 を足した値に設定する。こうすることで、ノードで障害が起きる前に送信された LSP が存在したとしても復帰したノードからの新しい LSP でそれを置き換えられるようになる。
LSP には生存時間 (time to live) も含まれる。これは一定の時間が経過した古い情報をネットワークから削除するために存在する。ノードは新しく受け取った LSP を隣接ノードに行き渡らせる前に必ず TTL を減少させる。また、ノードに保存されている LSP を「老化」させる処理も行う。いずれかの LSP の TTL が 0 になると、ノードは TTL を 0 に設定した LSP を隣接ノードに送信する。TTL が 0 の LSP は「この LSP を削除せよ」を意味するメッセージとして解釈される。
経路の計算
他の全てのノードが送信した LSP のコピーを手に入れたノードは、ネットワークのトポロジーを表す完全な地図を計算できる。その地図があれば任意の宛先への最良の経路が分かるはずである。続いての問題は「LSP の情報から経路を具体的にどうやって計算するのか」となる。グラフ理論でよく知られたアルゴリズム ── ダイクストラのアルゴリズム ── がこの問題に対する解決策となる。
まずダイクストラのアルゴリズム (Dijkstra's algorithm) をグラフ理論の言葉で定義する。ノードが受け取った LSP を使ってネットワークのグラフ表現を構築したとする。そのグラフの頂点の集合を \(N\) と表し、頂点 \(i\) と頂点 \(j\) を結ぶ辺のコスト (非負) を \(l(i,j)\) と表す。二頂点に辺が存在しない場合は \(l(i, j) = \infty\) とする。以下の説明では、アルゴリズムを実行して他のノードとの最小コスト路を見つけようとしている頂点を \(s \in N\) とする。アルゴリズムは二つの変数を管理する:
-
\(M\): アルゴリズムによる処理が完了した頂点の集合
-
\(C(n)\): 頂点 \(s\) と頂点 \(n\) を結ぶ暫定的な最小コスト路のコスト
ダイクストラのアルゴリズムは次のように動作する。最初 \(M\) には \(s\) だけが含まれ、各頂点へのコストからなる配列 \(C(n)\) は \(s\) に直接接続するノードのコストを使って初期化される。続いて \(M\) から到達可能な頂点の中でコストが最も小さいものを \(w\) として選択し、\(M\) に追加する。最後に、未処理の頂点 \(n\) に対して \(w\) を通って頂点に到達する路のコストを既存の (\(w\) を通らない) 路のコストと比較することで配列 \(C(n)\) を更新する。ダイクストラのアルゴリズムの疑似コードを次に示す:
実際には、各ルーターは収集した LSP から経路テーブルを直接計算するとき前方検索アルゴリズム (forward search algorithm) と呼ばれるダイクストラのアルゴリズムの一種を利用する。具体的に説明すると、このアルゴリズムにおいて各ルーターは Tentative (暫定的) と Confirmed (確認済) という二つのリストを管理する。二つのリストには (宛先, コスト, ネクストホップ) の形をしたエントリーが含まれ、前方検索アルゴリズムは次のように動作する:
-
自身を表すエントリーで
Confirmedを初期化する。このエントリーのコストは 0 となる。 -
一つ前のステップで
Confirmedに追加された頂点のそれぞれ (Next) に対して、その LSP を選択する。 -
Nextに隣接するノードのそれぞれ (Neighbor) に対して、Neighborに到達するためのコスト (Cost) を計算する。Costは自身からNextまでのコストとNextからNeighborまでのコストの和として計算できる。-
Neighborに対応するエントリーがConfirmedにもTentativeにも含まれていないなら、(Neighbor, Cost, NextHop)をTentativeに追加する。ここでNextHopは自身がNextに向かうとき初めに通過するノードを表す。 -
Neighborに対応するエントリーが現在Tentativeに含まれており、そのエントリーに記録されているコストよりCostの方が小さいなら、そのエントリーを(Neighbor, Cost, NextHop)で置き換える。ここでNextHopは自身がNextに向かうとき初めに通過するノードを表す。
-
-
Tentativeが空なら、アルゴリズムを終了する。そうでなければ、Tentativeから最もコストの小さいエントリーを選び、それをConfirmedに入れ、ステップ 2 に戻る。
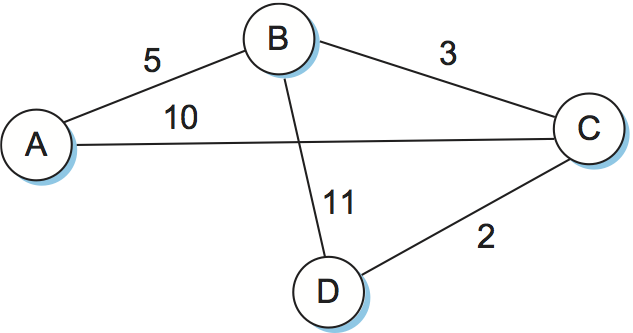
例を見れば理解がずっと簡単になるだろう。図 89 に示すネットワークを考える。一つ前の例と異なり、今回は各辺が異なるコストを持つ。ノード D におけるルーティングテーブル構築の各ステップを表 20 に示す。D の二つの出力先を結ばれているノードの名前 (B と C) で表記している。アルゴリズムは間違った経路 (B に直接到達するコスト 11 の経路など) を選びかけることがあるものの、最終的には全てのノードに対する最小コスト路を計算できている点に注目してほしい。
| ステップ | Confirmed |
Tentative |
備考 |
|---|---|---|---|
| 1 | (D,0,–) |
Confirmed に新しく追加されたのは D だけなので、その LSP を見る。 |
|
| 2 | (D,0,–) |
(B,11,B), (C,2,C) |
D の LSP によると、D は B にコスト 11 で直接到達できる。これは記録されたエントリーのコスト (無限大) より小さいので、この経路を表すエントリーを Tentative に追加する。C についても同様。 |
| 3 | (B,11,B), (C,2,C) |
(B,11,B) |
Tentative のエントリーでコストが最小の (C, 2, C) を Confirmed に移す。次のステップでは新しく Confirmed に移った C の LSP を調べる。 |
| 4 | (D,0,–), (C,2,C) |
(B,5,C), (A,12,C) |
C を経由して B に到達するコストは 5 なので、この路を表すエントリー (B,5,C) で (B,11,B) を置き換える。C の LSP からは A にコスト 12 で到達できることも分かる。 |
| 5 |
|
(A,12,C) |
Tentative のエントリーでコストが最小の (B,5,C) を Confirmed に移す。続いて B の LSP を確認する。 |
| 6 |
|
(A,10,C) |
B を経由すれば A にコスト 10 で到達できるので、Tentative エントリーを置き換える。 |
| 7 |
|
Tentative のエントリーでコストが最小の (A,10,C) を Confirmed に移す。Tentative が空になったので終了。 |
リンク状態型ルーティングのアルゴリズムは様々な優れた特徴を持つ: 素早く安定化することが証明されており、生成されるトラフィックの量も多くない。さらに、トポロジーの変化やノードの障害にも迅速に応答できる。一方で欠点としては、各ノードに保存される情報 (ネットワーク内の自身を除く全てのノードからの LSP) が非常に大きい点が挙げられる。これはルーティングにおける基礎的な問題の一つであり、スケーラビリティという一般的な問題の例と言える。特定の問題 (各ノードが必要とする可能性のあるストレージの問題) と一般的な問題 (スケーラビリティの問題) の両方に対するいくつかの解決策は次節で議論される。
教訓
距離ベクトル型ルーティングとリンク状態型ルーティングはどちらも分散ルーティングアルゴリズムではあるものの、異なる戦略を採用する。距離ベクトル型ルーティングでは、各ノードが直接接続された隣接ノードだけと対話し、そのとき自身が知っている全ての知識 (つまり全てのノードに対する距離) を送り合う。これに対してリンク状態型ルーティングでは、各ノードが他の全てのノードと対話し、そのとき自身が確実に知っている知識 (直接接続されたリンクの状態) だけを送り合う。第 3.5.3 項で SDN (software defined network, ソフトウェア定義ネットワーク) を紹介するときは、より中央集権的なルーティングのアプローチを考察する。
OSPF (Open Shortest Path First Protocol)
最も広く使われるリンク状態型ルーティングプロトコルの一つに OSPF (Open Shortest Path First Protocol) がある。最初の「Open」は OSPF が IETF (Internet Engineering Task Force) の後援で作成されたオープンかつ非プロプライエタリな規格であることを示す。次の「Shortest Path First」はリンク状態型ルーティングの別名から来ている。OSPF はここまでに解説した基本的なリンク状態型ルーティングのアルゴリズムに様々な機能を追加している。OSPF が持つ機能の一部を示す:
-
ルーティングメッセージの認証 ── 分散ルーティングアルゴリズムの特徴の一つとして、一つのノードが多数のノードに情報を広めることが挙げられる。このため、プロトコルに参加するノードが全て信用できることを確認するのは良いアイデアである。ルーティングメッセージの認証は信用の確立に役立つ。初期バージョンの OSPF は単純な 8 バイトのパスワードを使った認証を使っていた。これは認証形式として十分ではなく、明確な悪意を持った技術力の高いユーザーの認証を妨げることはできないものの、誤設定や簡単な攻撃で発生する問題の一部を緩和することはできる (似た形式の認証は RIP にもバージョン 2 で追加された)。後に強力な暗号認証が追加された。
-
階層化 ── 階層構造はシステムをスケーラブルにするために利用される基礎的なツールの一つである。OSPF は一つのドメインをエリア (area) に分割できるようにすることで、ルーティングに新たな階層を追加する。これはルーターが同じドメイン内の全てのネットワークに到達する方法を知る必要がなくなることを意味する ── 正しいエリアに到達する方法さえ知っておけば転送を行える。このため、各ノードが送り合う情報および保存する情報が削減される。
-
ロードバランシング ── OSPF では同じコストを持つ同じ場所への複数の経路を同時に利用できる。トラフィックはそれらの経路で公平に振り分けられ、利用可能なネットワーク帯域を効率良く利用できる。
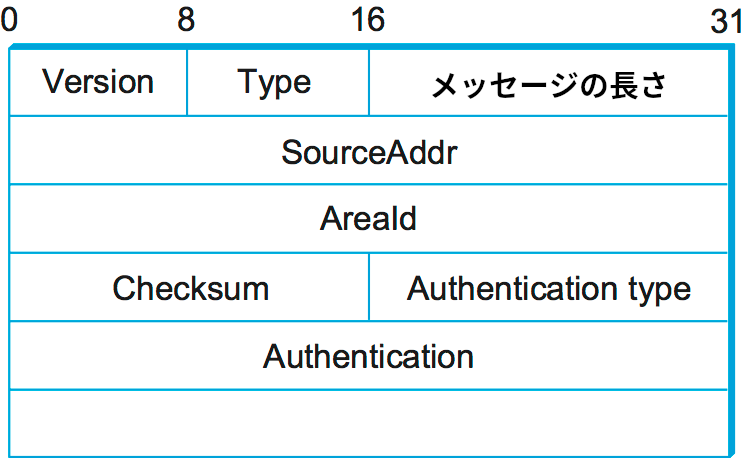
OSPF メッセージにはいくつか異なる種類が存在するものの、先頭のヘッダー (図 90) は共通している。Version フィールドは現在 2 で固定であり、Type フィールドは 1 から 5 の値を取る。SourceAddr フィールドはメッセージの送信元を識別し、AreaId フィールドは送信元ノードが属するエリアを表す 32 ビットの識別子である。認証データを除くパケット全体は IP ヘッダーと同様のアルゴリズムを用いる 16 ビットのチェックサムで保護される。Authentication type フィールドには認証を使わないなら 0、単純なパスワードを用いるなら 1、暗号チェックサム認証を用いるなら 2 を設定する。認証を用いるときは、Authentication フィールドにパスワードあるいは暗号チェックサムを設定する。
五つある OSPF のメッセージタイプのうち、タイプ 1 は「Hello パケット」を表す。前述したように、Hello パケットは自身が生きていて接続されていることを知らせるために隣接ノードへ送られるパケットである。他のタイプはリンク状態メッセージの送信、要求、要求に対する返答、そして確認応答に利用される。OSPF におけるリンク状態メッセージの基本的な構成単位は LSA (link-state advertisement) と呼ばれる。一つのメッセージは複数の LSA を含むことができる。以降では LSA の詳細を少し説明する。
どんなインターネットワーク用のルーティングプロトコルとも同じように、OSPF は様々なネットワークに到達する方法に関する情報を提供しなければならない。そのため、OSPF は前述したグラフベースの単純なプロトコルの他にも情報をいくつか提供する必要がある。具体的には、OSPF を実行するルーターは自身と直接接続する一つ以上のネットワークを広報するリンク状態パケットを送る可能性があり、加えて他のルーターに直接接続するルーターはそのルーターと自身を結ぶリンクのコストを広報する必要がある。これらの二つの種類の広報はドメイン内の全てのルーターがドメイン内の各ネットワークに対するコストとネクストホップを適切に計算するために必要となる。
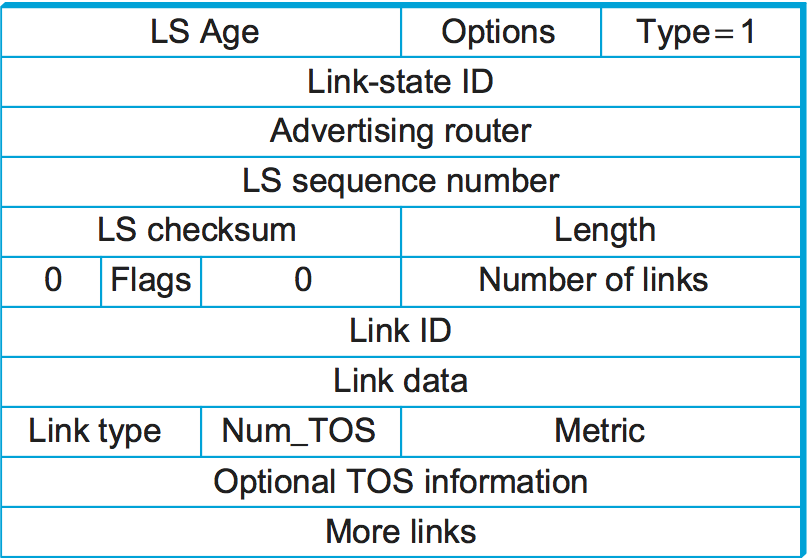
図 91 にタイプ 1 のリンク状態広報で使われるパケットのフォーマットを示す。タイプ 1 の LSA はルーター同士を結ぶリンクのコストを広報する。タイプ 2 の LSA はルーターが自身の接続するネットワークを広報するために利用され、他のタイプは先述した追加の階層構造をサポートするために利用される。LSA のフィールドの多くはこれまでの議論から明らかなはずである。LS Age フィールドは基本的に TTL (time to live) のことだが、このフィールドは時間が経過すると大きくなっていき、事前に定義された最大値になったときに LSA が期限切れとなる点が通常の TTL と異なる。Type フィールドはこれがタイプ 1 の LSA であることを示す。
タイプ 1 の LSA では Link-state ID フィールドと Advertising router フィールドが一致し、この LSA を作成したルーターを表す 32 ビットの識別子が両方のフィールドに設定される。この識別子を割り当てる戦略はいくつか考えられるものの、ルーティングドメイン内で一意であること、そしてルーターが割り当てられた識別子を一貫して使い続けることがプロトコルの正しい動作のために不可欠となる。こういった要件を満たすルーターの識別子を選択する方法の一つとして、ルーターに割り当てられた IP アドレスの中で最も小さいものを選ぶ方法がある (ルーターはインターフェースごとに異なる IP アドレスを持つ可能性があることを思い出してほしい)。
LS sequence number フィールドは先述したのと全く同じ仕組みで古い (あるいは重複した) LSA を検出するために存在する。LS checksum フィールドは他のプロトコルで見てきたものと同様である: このフィールドは、もちろん、データが破損していないことを確認するために存在する。LS checksum フィールドはパケット内の LS Age を除く全てのフィールドから計算されるので、LS Age を増加させたときにチェックサムを再計算する必要はない。Length フィールドは完全な LSA の長さをバイトで表す。
以降は実際のリンク状態に関する情報となる。この部分は TOS (type of service, サービスのタイプ) 情報があるので多少複雑になっている。一旦 TOS は無視すると、LSA に対応するリンクは Link ID と何らかの Link Data、そして metric フィールドで表される。最初の二つのフィールドはリンクを識別する。リンクの端にあるルーターの識別子を Link ID として、必要なら Link Data を使って複数のリンクから一つを選択する方法がよく使われる。metric フィールドは当然リンクのコストを表す。Type フィールドはリンクに関する情報 ── 例えばポイントツーポイントリンクかどうかなど ── を伝える。
TOS に関する情報は OSPF が IP パケットの TOS フィールドの値に基づいて異なる経路を選べるようにするために存在する。どんなときでも単一のメトリックを使うのではなく、TOS の値に応じて異なるメトリックを使い分けることができる。例えばネットワークの中に低遅延が要求されるトラフィックに適したリンクがあるなら、TOS の値が低遅延を表すときはそのリンクに低いコストを与え、それ以外のときは高いコストを与えることができる。こうすると OSPF は IP パケットの TOS フィールドの値に基づいて異なる最短路を選択する。なお執筆時点において、この機能はあまり実用されていない。
3.4.4 メトリックの選択
ここまでの議論はルーティングアルゴリズムの実行時にリンクのメトリック (コスト) が決まっていることを仮定していた。本項では、実際のネットワーク運用で効率的であることが示されているリンクコストの計算方法をいくつか紹介する。これまでに見たコストの計算方法の一つに、全てのリンクにコスト 1 を割り当てる方法がある ── おかしな考え方ではなく、非常に単純で、最小コスト経路は最小ホップ経路に等しくなる。しかし、こういったアプローチにはいくつか欠点がある。第一に、各リンクのレイテンシが区別されない。そのためルーティングアルゴリズムから見ると 250 ms のレイテンシを持つ衛星回線が 1 ms のレイテンシを持つ地上回線と同程度に魅力的に見える。第二に、各経路の帯域が区別されない。つまり 1 Mbps のリンクを通る経路が 10 Gbps のリンクを経路と事実上同じになる。最後に、各リンクに対する現在の負荷が区別されない。そのため負荷が高いリンクの迂回は不可能になる。最後の問題が最も難しいことが経験から示されている。この問題を解くには複雑で動的なリンクの特性をコストという単一のスカラーで表さなければならないためである。
ARPANET はリンクコスト計算の様々なアプローチの実験台となった (余談: リンク状態型ルーティングが距離ベクトル型ルーティングより安定性の面で優れることが示されたのも ARPANET だった。最初のバージョンでは距離ベクトル型が使われ、後のバージョンではリンク状態型が使われた)。以降では ARPANET におけるルーティングメトリックの進化をたどりながら、問題の細かい側面を詳しく見ていく。
オリジナルの ARPANET はルーティングメトリックとしてリンクで転送待ちキューに存在するパケットの個数を利用した。例えば 10 個のパケットを待たせているリンクには 5 個のパケットを待たせているリンクより大きなコストが割り当てられる。しかし、このメトリックを使ったルーティングは上手く動作しなかった。転送待ちキューの長さは人工的な負荷の指標であり、パケットの移動先が宛先に近いとは限らないためである。買い物の順番待ちをしているときはこれで十分かもしれないが、目的地に移動したいときは十分でない。より正確に表現すれば、ARPANET が最初に採用したルーティングメトリックは帯域とレイテンシを考慮しないという問題を抱えている。
ARPANET における次バージョンのルーティングアルゴリズムでは、リンクの帯域と遅延が考慮され、転送待ちキューの長さだけではなく遅延も負荷の指標として利用された。これは次のように動作する。まず、届いたパケットのそれぞれに対してルーターは到着時刻のタイムスタンプ (ArrivalTime) が記録する。同様にルーターからパケットが送られた時刻 DepartTime もパケットに記録する。次に、リンクレベルの ACK が宛先から返ってきたとき、ルーターはそのパケットの遅延 (Delay) を次のように計算する:
Delay = (DepartTime - ArrivalTime) + TransmissionTime + Latency
ここで TransmissionTime と Latency はリンクに対して静的に定義された値であり、それぞれリンクの帯域とレイテンシから定まる。この式の DepartTime - ArrivalTime はルーターの負荷が原因で発生した遅延 (待ち時間) であることが分かる。もし ACK が返ってこないままタイムアウトしたときは、DepartTime は再送の時刻に再設定される。こういったケースでは DepartTime - ArrivalTime がリンクの信頼性を捉えることになる ── パケットの再送が頻繁に発生するリンクは信頼性が低いので、利用を避けるのが望ましい。最後に、各リンクに割り当てられる重みは最近そのリンクを通して送られたパケットで発生した遅延の平均から計算される。
最初の仕組みと比べれば改善は見られるものの、このアプローチも多くの問題を抱えている。負荷が低い間は静的な項 (TransmissionTime + Latency) が Delay を支配するのでそれなりに上手く動作する。しかし負荷が高まると、輻輳を起こしたリンクが非常に高いコストを広報するようになる。すると全てのトラフィックがそのリンクを避けるようになり、最終的にそのリンクはアイドルになる。しばらくするとそのリンクは低いコストを広報するので、全てのトラフィックを引き付けて再び輻輳を起こしてしまう。以上の状況は繰り返し発生する。この不安定性によって、高負荷時に多くのリンクが長い時間をアイドルで過ごすようになる。これは高負荷時に絶対に避けなければならないことである。
もう一つの問題として、コストの範囲が非常に大きくなることがある。例えば高負荷の 9.6 Kbps リンクは低負荷の 56 Kbps より 127 倍コストが高い、といった状況があり得る (1975 年ごろの ARPANET の話をしていることを思い出してほしい)。これは、ルーティングアルゴリズムが負荷の高い 9.6 Kbps リンクの 1 ホップよりも負荷の低い 56 Kbps リンクの 127 ホップを優先して選択することを意味する。高負荷のリンクに向かうトラフィックを減らすのは良いアイデアであるものの、トラフィックを全く受け取らなくなるほどにコストを上げるのは度を越している。1 ホップで済むときに 126 ホップを選択するのは一般にネットワークリソースの無駄遣いである。加えて、この計算式だと衛星リンクのコストが過度に高くなる。アイドルの 56 Kbps 衛星リンクはアイドルの 9.6 Kbps 地上リンクより非常に大きなコストを持つが、高帯域が必要なアプリケーションでは衛星リンクの方が高いパフォーマンスが出る場合もある。
三つ目のアプローチはこういった問題を解決する。主要な変更点はコストのダイナミックレンジ2を大きく圧縮したこと、リンクの種類を考慮したこと、そして時間と共にコストを滑らかに変化させるようにしたことである。
コストの滑らかな変化はいくつかの仕組みによって達成される。まず、遅延はリンクの利用率に取って代わられ、急激な変化を押さえるために前回の利用率の値との平均が使われる。次に、測定サイクルの間におけるメトリックの変化量に上限が設けられた。コストの変化を滑らかにすることで、全てのノードが特定の経路を使わなくなる可能性が大きく低下する。
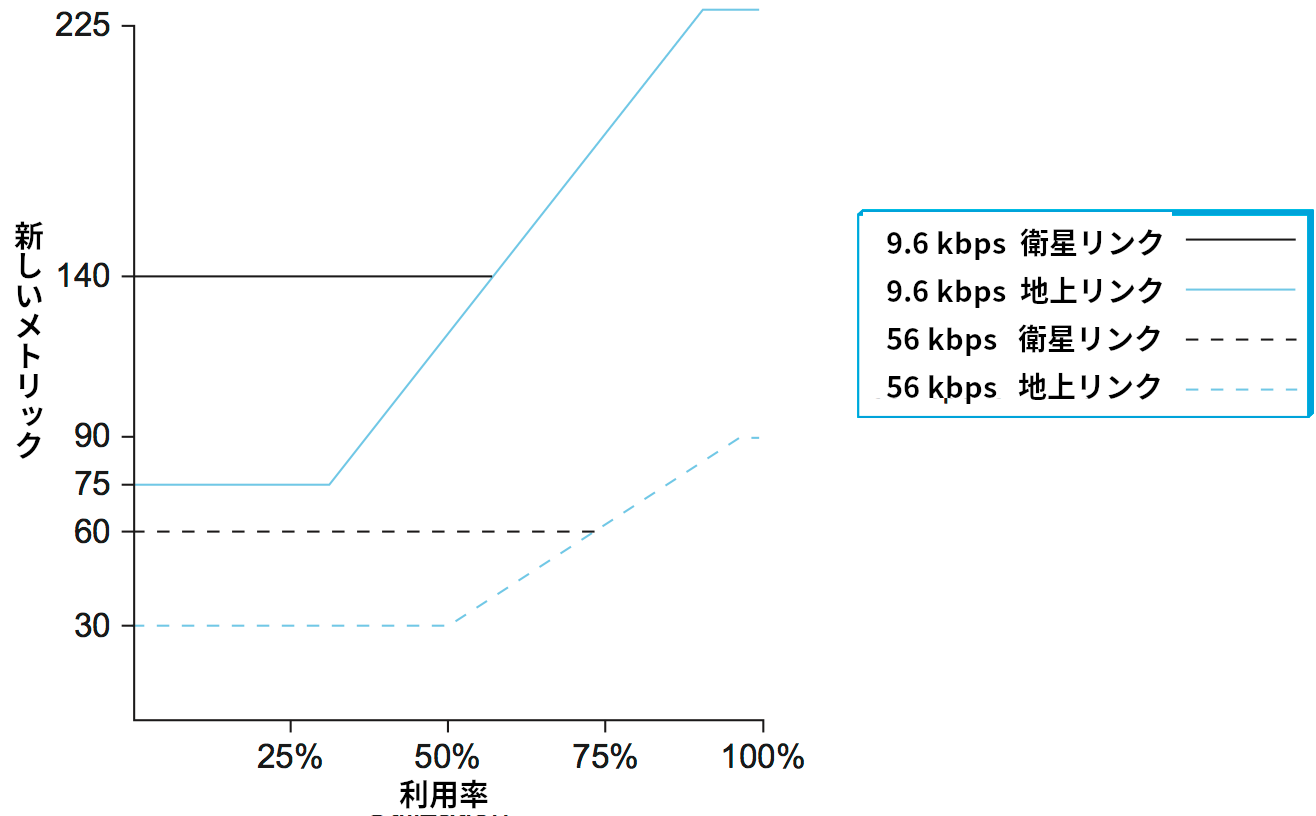
ダイナミックレンジの圧縮は測定された利用率、リンクの種類、リンクの速度を図 92 に示された関数に入力することで行われる。このグラフからは次のことが分かる:
-
高負荷のリンクに対するコストはアイドル時のコストの 3 倍より大きくならない。
-
最も高価なリンクは最も安価なリンクの 7 倍のコストしか持たない。
-
高速な衛星リンクは低速な地上リンクよりコストが低い。
-
負荷が中程度、もしくは高いときに限ってコストが利用率の関数となる。
こういった事項はどれも、あるリンクが全てのルーターから使われなくなる可能性が格段に低くなることを意味している。コストに上限が設けられたので、リンクがいくつかの経路に対して魅力的でなくなったとしても、他のリンクにとっては最良の選択肢であり続ける可能性が高まるためである。図 92 に示された関数の傾き、オフセット、曲線の分割点は長い試行錯誤によって定まったものであり、優れたパフォーマンスを提供するよう注意深く調整されている。
ARPANET におけるこういった改善の歴史が存在するにもかかわらず、現実世界で運用されるネットワークの大部分ではメトリックの変更はまず起こらない。仮に起こったとしてもネットワーク管理者によって行われるだけで、ここで説明したように自動的に起こることはない。この理由の一端は、「メトリックの動的な変更は不安定すぎて使えない」という意見が一般的な通念になったことにある (おそらくそんなことはないのだが)。それよりも重要と思われる点として、現代の多くのネットワークではリンクの速度とレイテンシに ARPANET が対処しなければならなかったほどの大きな格差が存在しない事実がある。そのため、現代では静的なメトリックが標準となっている。リンクの帯域の逆数に定数を乗じた値をコストに設定するアプローチがよく使われる。
教訓
現代では使われていない何十年も前のアルゴリズムがいまだに解説されているのはなぜだろうか? その理由は、二つの重要な教訓がここから得られるからである。まず、コンピューターシステムは経験に基づいて反復的に設計される。最初から上手く設計できることはまずないのだから、単純な解決策を早く使ってみて、そこから時間をかけて改善していく心構えが重要となる。通常、設計フェーズに長い時間をかけるのは良い計画ではない。二つ目の教訓はよく知られた KISS 原則「単純にしておけ、馬鹿者」である。複雑なシステムの構築では「小さい方が大きい」ことがよくある。洗練された最適化を行える機会は多くあり、その機会を無駄にするのは惜しいように思える。そういった最適化が短期的な価値を生むことも確かにあるものの、時間が経つと単純なアプローチが最も優れていると判明することは驚くほど頻繁にある。これは可動部品を多く持つシステム (例えばインターネット) では各部分を可能な限り単純に保つのが最も優れたアプローチであることが多いためである。