8.2 暗号学的な構成要素

本章では暗号学ベースのセキュリティに関する様々な概念を一つずつ紹介していく。本節では最初のステップとして暗号学的アルゴリズム ── 暗号と暗号学的ハッシュ関数 ── を紹介する。これらのアルゴリズムは直接セキュリティに役立つわけではなく、セキュリティに役立つ仕組みで重要な構成要素となる。暗号学的アルゴリズムは鍵 (key) というパラメータを持ち、第 8.3 節では鍵を配布するときに生じる問題とその解決法を紹介する。第 8.4 節では、暗号学的な構成要素を組み合わせて正しい鍵を持つ二者の間にセキュアな通信を提供するプロトコルを構築する方法を説明する。最後に第 8.5 節では、実際に現在使われているセキュリティプロトコルおよびセキュリティシステムを詳しく見ていく。

8.2.1 暗号の原則

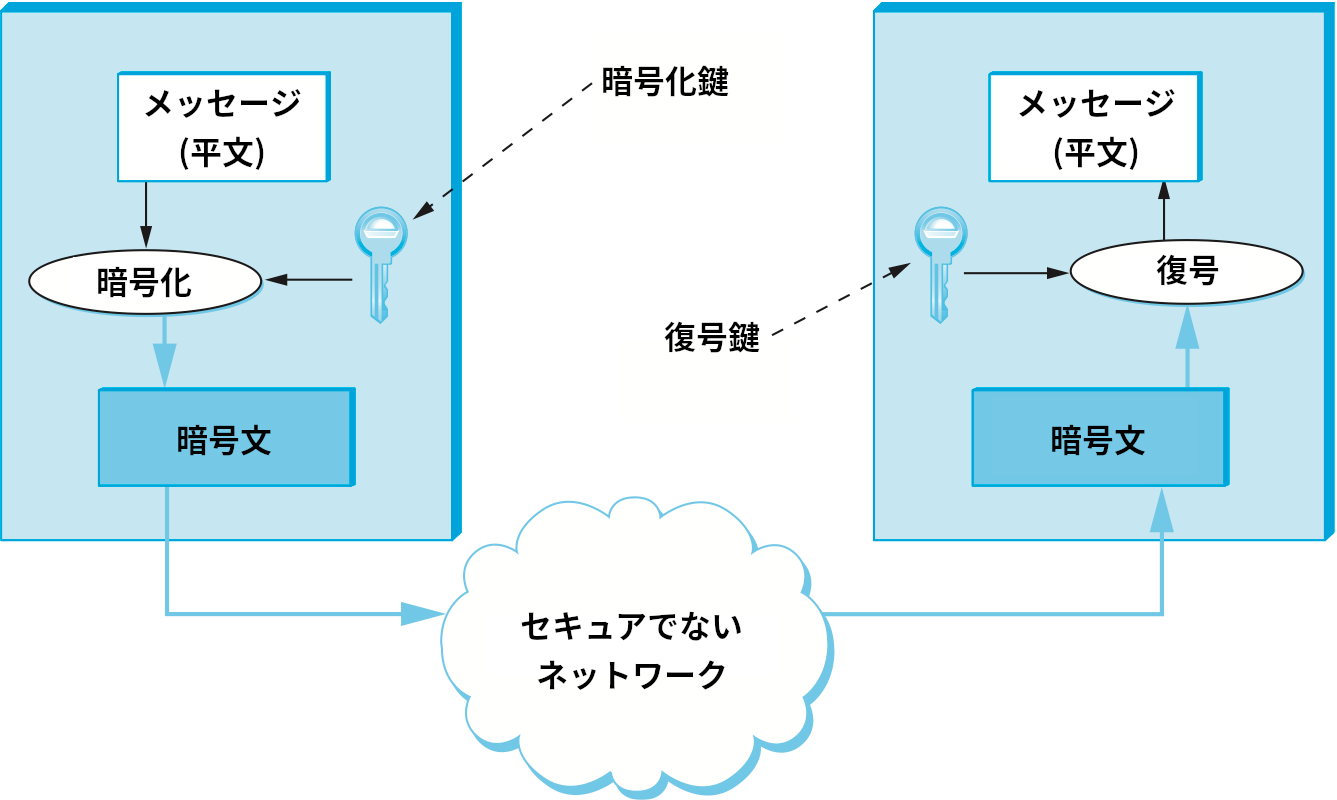
まず言葉を定義する。暗号化 (encryption) とは、メッセージに変換を施し、秘密にされた逆変換の方法を知らないと第三者が解読できないようにする処理を言う。送信者は相手に伝えたい平文 (plaintext) に暗号化を行う関数を適用し、得られた暗号文 (ciphertext) をネットワーク越しに転送する。メッセージの受信者は復号 (decryption) を行う秘密の関数 ── 暗号化関数の逆関数 ── を適用して平文を復元する。ネットワークを通じて送信される暗号文を第三者が盗聴できたとしても、受信者以外は復号関数を知らないので平文を得ることはできない。暗号化関数と復号関数によって表される変形を暗号 (cipher) と呼ぶ。暗号を使ってメッセージを送信する様子を図 195 に示す。

1883 年、暗号学者 Auguste Kerckhoffs は暗号に関する次の原理 (Kerckhoffs の原理) を提案した:

つまり秘密と仮定できるのは鍵だけで、暗号が敵対者に知られたとしても復号が可能になってはいけない。ここから、平文から生成された暗号文は暗号関数と鍵の両方に依存すると分かる。この原理が提案された理由の一つに、暗号の秘密性に頼ってしまうと、暗号が敵対者に知られたときに (鍵だけではなく) 暗号自体を変更しなければならないことがある。新しい暗号の開発は簡単ではないので、頻繁な暗号の交換は問題になる。また、暗号がセキュアかどうかを知る最も優れた方法の一つは長く使うことである ── もし誰にも破れないなら、その暗号はセキュアに違いない (暗号の突破を試みる人の中には突破に成功したときその事実を広く知らせる人が幸い多くいるので、便りが無いのは良い頼りである)。ここから、新しい暗号の開発・運用には多大なコストとリスクが伴うと言える。最後に、鍵でパラメータ化された暗号は大量の暗号からなる集合に事実上等しい。つまり鍵を切り替えれば新しい暗号が手に入る。このため暗号解読者 (cryptanalyst または code-breaker) が鍵と暗号を突破するために利用できるデータが少なくなり、仮に突破できたとしても手に入れられるデータは少なくて済む。

暗号アルゴリズムの基礎的な要件は、平文を暗号文に変換し、そのとき意図した通信相手 (復号鍵の所持者) だけが平文を復元できるようにすることである。つまり、鍵を持たない主体が暗号化されたメッセージを読めてはいけない。

暗号文を手にした攻撃者が持つ情報は暗号文だけではない事実を理解することは重要である。例えば、攻撃者は平文が英語であり、文字 "e" が他の文字より頻繁に出現することを知っているかもしれない。他の文字および文字の組み合わせに対する頻度も平文が英語で書かれていると分かれば予測できる。この情報によって鍵を見つける問題が格段に簡単になる可能性がある。同様に、攻撃者はメッセージに書かれる可能性の高い単語を知っているかもしれない。例えば、リモートログインセッションを始めるときに送信されるメッセージには「login」という単語が含まれる可能性が高い。この知識を使うと既知平文攻撃 (known plaintext attack) が可能になる。既知平文攻撃は何の知識も利用しない暗号文単独攻撃 (ciphertext only attack) より鍵を見つけられる可能性が高い。さらに優れているのは選択平文攻撃 (chosen plaintext attack) で、この攻撃は送信者が送信する可能性が高い情報を外部から送信者に与えられるときに行える ── 例えば戦争中の軍事報告に対して選択平文攻撃が仕掛けられたことがある。

以上の考察から、最良の暗号アルゴリズムでは攻撃者が平文と暗号文の両方を知っている場合でさえ鍵を推測できてはいけないことが分かる。このとき、攻撃者は可能な鍵を全て試す以外の選択肢を持たない ── しらみつぶしの総当たり (brute force) 探索しか行えない。鍵が \(n\) ビットのとき、鍵として可能な値は \(2^{n}\) 個存在する (\(n\) 個のビットそれぞれが \(0\) または \(1\) の値を取れる)。ここから、攻撃者が正しい鍵を見つけるまでにかかる試行回数の期待値は \(2^{n-1} + \frac{1}{2} \approx 2^{n-1}\) と計算できる。よって鍵を十分長くして鍵の確認処理のコストを無視できない程度に大きくすれば、鍵の探索にかかる計算量を非現実的なまでに大きくできる。ただし、問題を難しくするのがコンピューターの計算能力が向上し続けている事実で、以前には不可能だった量の計算が可能になっている。さらに、本書で考えているのはネットワークを通り抜けるデータのセキュリティである事実も話を複雑にする。そういったデータは短い時間だけ攻撃を受ける環境に晒されるのに対して、一般にセキュリティの研究者は数十年にわたってアーカイブに保存されるデータの脆弱性を考察する。長期間保存されるデータには気前よく大きな鍵を使うことができるものの、大きな鍵を使うと暗号化と復号は遅くなる。

多くの暗号はブロック暗号 (block cipher) と呼ばれる部類に属する。つまり、固定サイズのブロックの連なりとして平文を解釈する。各ブロックを独立に暗号化する単純な方式をECB モード (electronic codebook mode, 電子符号表モード) と呼ぶ。ECB モードには、同じ平文ブロックが必ず同じ暗号文ブロックに対応してしまうという弱点がある。このとき平文に何度も現れるブロックの存在が暗号文から分かるので、暗号解読者に対する大きなヒントとなる。

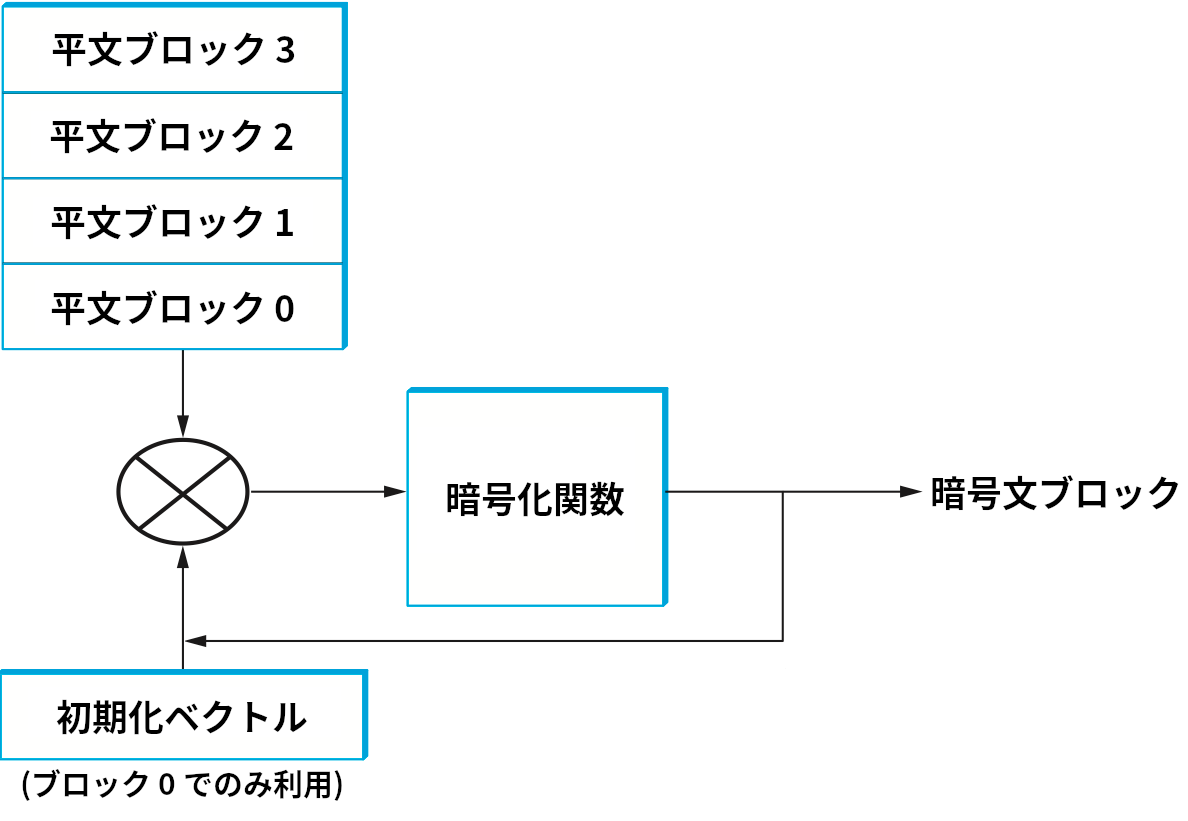
この問題を避けるために、ブロック暗号は各ブロックに対する暗号文が文脈に依存するように設計される。何を文脈とみなし、どのように文脈を利用するかを暗号の利用モード (mode of operation) と呼ぶ。よく使われる利用モードに CBC モード (cipher-block chaining mode, 暗号ブロック連鎖モード) がある。CBC モードにおいて、平文のブロックは一つ前のブロックの暗号文との XOR が取られてから暗号化される。こうすると各ブロックの暗号文は一つ前のブロックの暗号文に依存することになる (つまり、CBC モードでは直前のブロックの暗号文が文脈となる)。最初の平文ブロックは一つ前のブロックを持たないので、初期化ベクトル (initialization vector) と呼ばれる乱数との XOR が取られる。初期化ベクトルは復号処理でも使われるので、送信される暗号文ブロックの列に加えられる。CBC モードの模式図を図 196 に示す。CBC モードと異なるモードにカウンターモード (counter mode, CTR モード) がある。CTR モードではカウンターから得られる連続する値 (1, 2, 3, ...) を平文ブロックの暗号化で利用する。

8.2.2 秘密鍵暗号

秘密鍵暗号 (secret-key cipher) では、通信を行う二人の参加者が同じ鍵を共有する¹。言い換えれば、メッセージを特定の鍵で暗号化したとき、その暗号文の復号には同じ鍵が必要になる。もし図 195 に示した暗号が秘密鍵暗号なら、暗号化鍵と復号鍵は同一になる。秘密鍵暗号では両参加者が同じ秘密を共有するので、秘密鍵暗号は対称鍵暗号 (symmetric-key cipher) とも呼ばれる。秘密鍵暗号と対になるのは公開鍵暗号 (public-key cipher) であり、次の項で説明される。なお、次項で見るように公開鍵暗号では二人の参加者が異なる鍵を用いるので、公開鍵暗号を非対称鍵暗号 (asymmetric-key cipher) と呼ぶこともある。

NIST (National Institute of Standards and Technology, アメリカ国立標準技術研究所) は秘密鍵暗号の規格をいくつか策定している。NIST による最初の秘密鍵暗号規格は DES (Data Encryption Standard) であり、1976 年に策定された。DES に対する総当たり探索より優れた暗号学的攻撃は見つかっておらず、その意味では時の試練に耐えていると言える。しかし、DES が開発されてから総当たり探索は高速化した。DES の鍵は 56 個の独立したビットを持つ (鍵自体は 64 ビットで、 最後の 8 ビットはパリティに使われる)。上述したように、鍵の候補が \(2^{56}\) 個が存在する場合に総当たり探索を使うと平均して候補の個数の半分、つまり \(2^{55} \approx 3.6 \times 10^{16}\) 回の探索で正しい鍵を発見できる。大きな数だと思うかもしれない。しかし探索は簡単に並列化できるので、鍵の探索は手に入るだけのコンピューターを使って行える ── 現在では数千台のコンピューターを難無く調達できる (Amazon から借りれば一時間当たり一台数セントで済むだろう)。1990 年代の後半には既に、DES 鍵を数時間で見つけることが可能だった。これを受けて NIST は 1999 年に DES 規格を改訂し、DES はレガシーシステムでのみ利用するべきという文言を追加した。

1998 年、NIST は 3DES (Triple DES, トリプル DES) を標準化した。3DES は DES の鍵を長くすることで暗号解析に対する耐性を向上させた暗号である。3DES の鍵は 168 (= 3×56) 個の独立したビットを持ち、三つの DES 鍵として利用される。3DES の鍵が表す三つの DES 鍵を DES-key1, DES-key2, DES-key3 とするとき、平文ブロックの 3DES 暗号化は次のように行われる: まず平文ブロックを DES-key1 を使って DES で暗号化し、その結果を DES-key2 を使って DES で復号し、さらにその結果を DES-3 を使って DES で暗号化したものを最終的な暗号文ブロックとする。復号では DES-key3 による復号、DES-key2 による暗号化、そして DES-key1 による復号がこの順番で行われる。

3DES の暗号化が DES-key2 を使った復号を利用するのは、レガシーの DES システムとの相互運用を可能にするためである。レガシーの DES システムが鍵を一つだけしか持たない場合でも、DES-key1, DES-key2, DES-key3 の全てにその鍵を設定することで 3DES システムの暗号化関数で暗号化を行える: 最初の二つのステップは同じ鍵を使った暗号化と復号なので結果は最初の平文となり、事実上最後の暗号化だけが行われる。

3DES は DES の鍵の短さという問題を解決するものの、他の欠点は受け継いでいる。例えば DES は元々 IBM によってハードウェアで実装するものとして設計されたので、DES/3DES のソフトウェア実装は速くならない。加えて、DES/3DES は 64 ビットのブロックサイズを用いる: ブロックサイズは大きい方が効率的かつセキュアになる。

現在 3DES の役割は同じく NIST が策定した AES (Advanced Encryption Standard) と呼ばれる規格に取って換わられている。AES は Rijndaelラインダール と呼ばれる暗号アルゴリズム (の変種) を採用する。このアルゴリズムの名前は考案者 (Joan Daemen と Vincent Rijmen) の一人の名前から取られた。AES は 128, 192, 256 ビットの鍵長をサポートし、ブロック長として 128 ビットを採用する。ASE はソフトウェアとハードウェアの両方で高速に実装でき、必要とされるメモリが少ないため携帯機器にも適している。AES は数学的に証明されたセキュリティ的特徴を持ち、執筆時点において AES の安全性を大きく脅かすことに成功した攻撃は存在しない。

8.2.3 公開鍵暗号

秘密鍵暗号と異なる暗号の分類として公開鍵暗号 (public-key cipher) がある。秘密鍵暗号では両参加者が単一の鍵を共有するのに対して、公開鍵暗号ではそれぞれの参加者が鍵の組を独立に持つ。鍵の組には特定の関係があり、一つは暗号化に、もう一つは復号に利用される。鍵の所持者は復号鍵を秘密にすることで、自身だけが暗号を復号できるようにする。一方で暗号化鍵は公開し、誰でもメッセージを暗号化して自身に送れるようにする。このため復号鍵は私有鍵 (private key) と呼ばれ、暗号化鍵は公開鍵 (public key) と呼ばれる。明らかに、この手法は公開鍵から私有鍵を推測できないことを前提としている。また、公開鍵暗号を使うときは公開鍵を使って暗号化したメッセージの送信を誰でも行えることも分かる: そのメッセージを復号できるのは復号に必要な私有鍵を持つ主体だけとなる。図 197 に公開鍵暗号の模式図を示す。

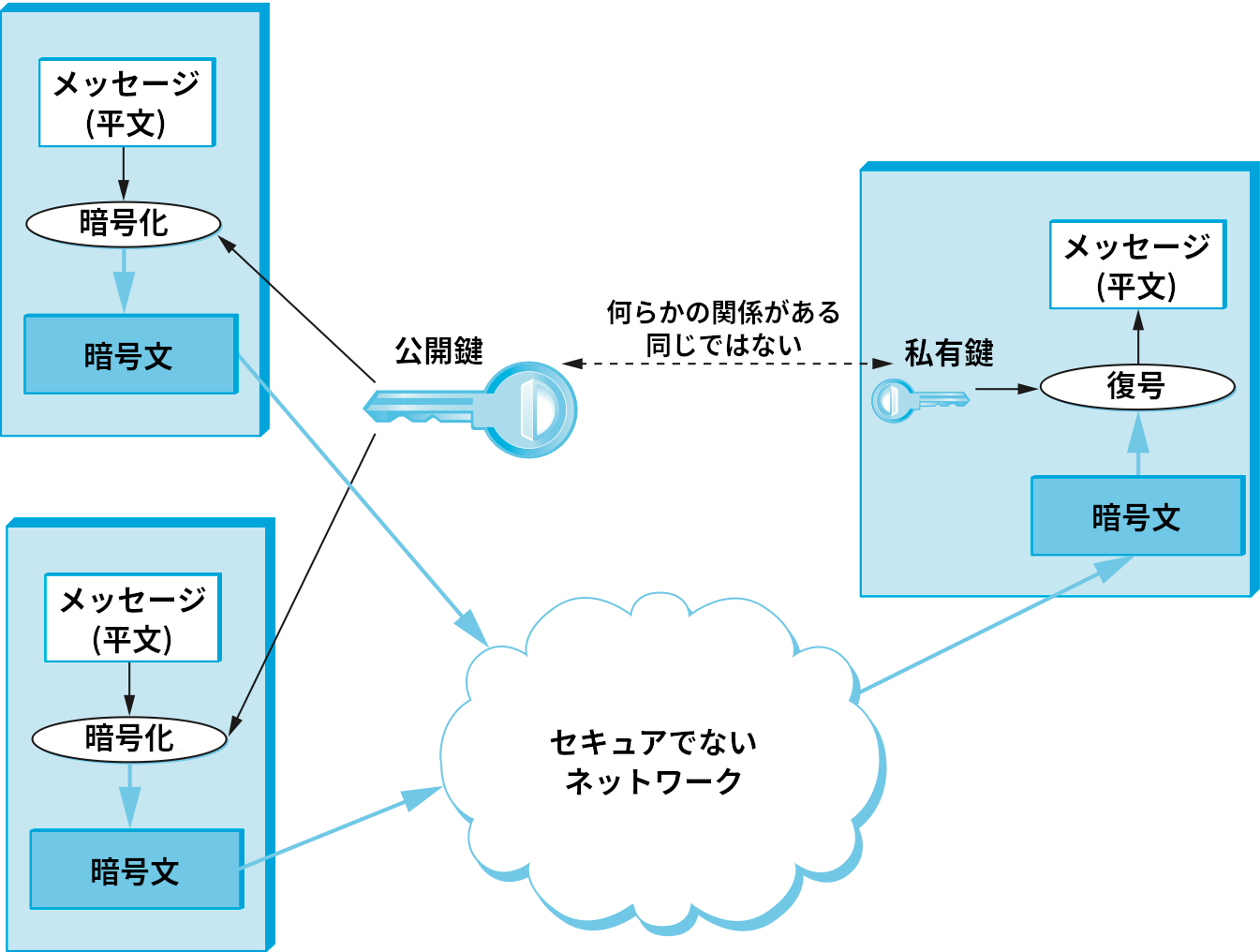
次の点は多少分かりにくいので強調しておく: 公開される暗号化鍵はメッセージの復号では役に立たない。暗号化鍵だけを知っている状態では、自分で暗号化した暗号文さえ復号できない。鍵が参加者を結ぶ通信チャンネルを定めると考えれば、公開鍵暗号と秘密鍵暗号の違いは鍵が定めるチャンネルのトポロジーに現れる。秘密鍵暗号では鍵が両参加者を結ぶ双方向通信チャンネルを定める ── それぞれの参加者は同じ (対称的な) 鍵を持ち、両者は自身のメッセージの暗号化と相手から届いた暗号文の復号を行える。これに対して公開鍵暗号では、公開鍵と私有鍵の組が多対一の片方向チャンネルを定める: 「多」は公開鍵を知っている大勢の人々であり、「一」は私有鍵の (唯一の) 所持者である。この事実は図 197 にも示されている。

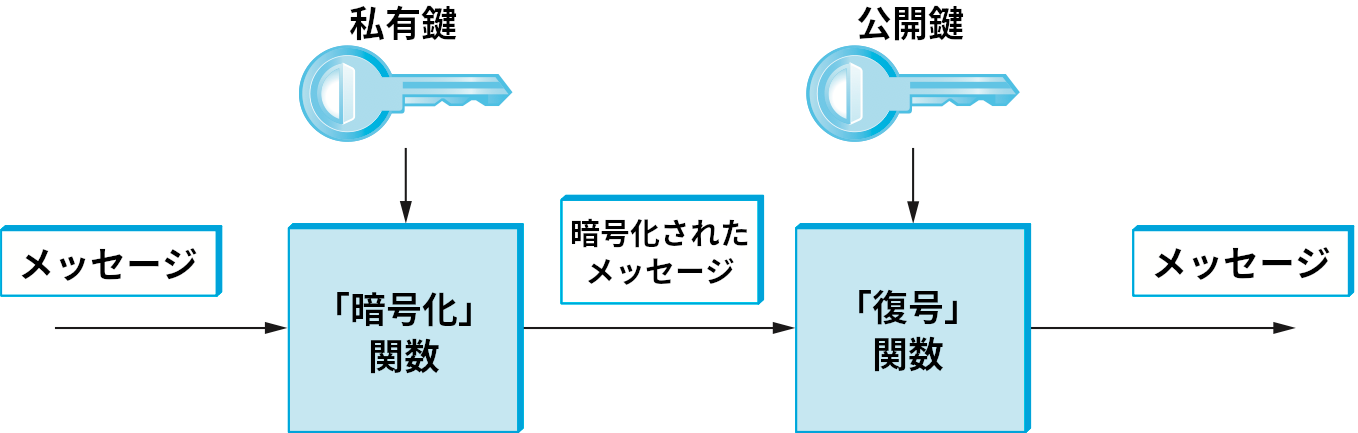
RSA などの一部の公開鍵暗号が持つ重要な特徴として、通常は復号に用いる私有鍵を使って「暗号化」を行うと、その「暗号文」を通常は暗号化に用いる公開鍵で「復号」できることがある (図 198)。私有鍵で暗号化したメッセージは公開鍵を知っていれば誰でも復号できるので、この特徴は機密性 (confidentiality) を提供する上で役立つわけではない (二人の参加者の間で双方向の機密性を提供するには、両者が鍵の組を所持し、お互いが相手の公開鍵でメッセージを暗号化する必要がある)。そうではなく、この特徴は認証 (authentication) を提供する上で役立つ: 私有鍵で暗号化されたメッセージの受信者は、そのメッセージの作成者が私有鍵の所持者以外にあり得ないと (後述する仮定の下で) 確信できる。

図 198 からも分かるように、上述した特徴を持つ公開鍵暗号では公開鍵を持ってさえいれば誰でも私有鍵で暗号化されたメッセージを復号できる。さらに、メッセージの復号結果が期待される値と一致することが確認できれば、メッセージが私有鍵で暗号化されたことを確信できる。第 8.2.4 項では、この操作を利用して認証が提供されることを説明する。次節で詳しく説明するように、公開鍵暗号は通信の最初で行われる認証と機密性を保った秘密鍵 (対称鍵) の交換で主に使われ、それ以降の機密性は秘密鍵暗号が提供する場合が多い。

興味深い歴史の話を一つ: 公開鍵暗号という概念は 1976 年に Whitfield Diffie と Martin Hellman によって最初に公に発表された。しかし後に公開された資料によると、イギリスの CESG (Communications-Electronics Security Group, 電子通信安全局) は 1970 年までには公開鍵暗号を発見していたことが明らかになっている。さらにアメリカの NSA (National Security Agency, 国家安全保障局) は 1960 年代の半ばに公開鍵暗号を発見したと主張している。

最もよく知られた公開鍵暗号は RSA である。RSA は考案者の Ronald Rivest, Adi Shamir, Leonard Adleman の頭文字を取って名付けられた。RSA の安全性は大きな整数の素因数分解は計算量的コストが高いという仮定に支えられている。数学者は整数を効率的に素因数分解する方法を RSA が発表された 1978 年よりずっと前から探し続けているものの見つけられていない。加えて、RSA が発表されてから現在まで RSA の解読に成功したという報告は存在しないので、RSA のセキュリティは非常に強固だと考えられている。しかし残念なことに、RSA をセキュアに利用するには 1024 ビット以上の長い鍵が必要になる。これは秘密鍵暗号の鍵より長い。なぜなら、RSA では鍵の組に関連付いた大きな整数の素因数分解を見つければ私有鍵を見つけられるのに対して、秘密鍵暗号では鍵空間に含まれる全ての鍵をしらみつぶしに試すことでしか秘密鍵を見つけられないためである。

RSA と異なる公開鍵暗号として ElGamal がある。RSA と同様、ElGamal の安全性は離散対数問題と呼ばれる数学的問題の難しさに支えられている。もちろん離散対数問題の効率的な解法は見つかっていない。ElGamal は 1024 ビット以上の鍵長を必要とする。離散対数問題には楕円曲線上の演算を利用する変種が存在し、この問題は通常の離散対数問題より計算がさらに難しいと考えられている。この問題を利用する暗号を楕円曲線暗号 (elliptic curve cryptography) と呼ぶ。

残念ながら、公開鍵暗号は秘密鍵暗号より計算速度が数桁劣る。そのため通信の大部分では秘密鍵暗号が使われ、公開鍵暗号は最初に行われる認証とセッション鍵の生成で利用される。

8.2.4 認証

暗号化は完全性 (integrity) を提供しない。暗号文が改竄されたとしても、復号された平文がそれらしい見た目をしていれば受信者は改竄を見抜けない。同様に、暗号化は認証 (authentication) を提供しない。メッセージが改竄された可能性が捨てきれないのなら、メッセージが特定の参加者から送られたことはどうやっても確信できない (ある意味で、完全性と認証は本質的に切り離せない概念と言える)。

認証子 (authenticator) とはメッセージと一緒に送られる値であって送り主の認証とメッセージの完全性の検証に利用されるものを言う。第 8.4 節では様々なプロトコルで認証子がどのように利用されるかを見る。ここでは認証子を生成するアルゴリズムに焦点を当てる。

第 2.4 節では、メッセージに意図せず混入したビット誤りを受信者が検出できるようにメッセージに追加されるチェックサムや巡回冗長検査 (CRC) 説明した。同様の考え方は認証でも利用できる。ただし認証では、攻撃者によって検出されないように行われる作為的なメッセージの改変を検出するための対策が必要となる。認証をサポートするために、認証子にはメッセージの送信者とされる主体だけが知っているはずの秘密を認証子の作成者が持っていることの証明が含まれる。例えば秘密は鍵で、証明は鍵で暗号化された値かもしれない。メッセージに追加される冗長な情報の形式と秘密を保持することの証明の形式は互いに依存する。本項ではいくつかの選択肢を議論する。

最初はメッセージに機密性は必要ないと仮定する ── つまり送信されるのは平文のメッセージと認証子であり、そのメッセージを認証する方法を考えることにする。機密性が要求されるケースは後で考える。

認証子の一つとして、暗号化と暗号学的ハッシュ関数 (cryptographic hash function) を組み合わせるものがある。暗号学的ハッシュ関数は暗号学的チェックサム (cryptographic checksum) とも呼ばれ、そのアルゴリズムは暗号のアルゴリズムと同様に公開知識とみなされる。暗号学的ハッシュ関数はメッセージを入力に受け取り、改竄を検出するのに十分な長さを持つ冗長な情報を出力する。通常のチェックサムや CRC がリンクに対するノイズから生じるビット誤りを検出するために設計されるのと同様に、暗号学的ハッシュ関数は攻撃者による作為的なメッセージの改竄を検出するように設計される。暗号学的ハッシュ関数の出力はメッセージダイジェスト (message digest) と呼ばれ、通常のチェックサムと同様にメッセージに付け足される (メッセージダイジェストは単にダイジェストとも呼ぶ)。メッセージダイジェストは入力されたメッセージの長さに関わらず同じ長さを持つ。そのため可能な入力メッセージの空間は可能なメッセージダイジェストの空間より大きく、ハッシュテーブルで衝突が起こるのと同じように、同じメッセージダイジェストを出力する異なるメッセージが必ず存在する。

メッセージダイジェストを暗号化して得られる暗号文は認証子として利用できる。この認証子とメッセージを受け取った受信者は、認証子を復号して得られる平文と受け取ったメッセージから計算したダイジェストが一致するかを確認すれば認証を行える。もし両者が一致するなら、受信者は (受け取った認証子が正しい鍵で暗号化されていることから) メッセージが本当に送信者とされる主体からのものであり、改竄もされていないと確信できる。仮に攻撃者が偽造されたメッセージと偽造された認証子を送信できたとしても、送信者の暗号化鍵を知らない攻撃者はダイジェストを正しく暗号化できないので受信者を騙すことはできない。

ただし、攻撃者は送信される平文と暗号化されたダイジェストを盗聴によって知ることはできる。さらに、攻撃者はメッセージから (公開されているハッシュ関数を使って) ダイジェストを計算できるので、同じダイジェストを生成する異なるメッセージを探すことができればメッセージの改竄が可能になる: 見つかったメッセージを元々の認証子と一緒に送信すれば受信者は改竄を検出できない。このため、セキュリティを提供するにはハッシュ関数に一方向性 (one-way) と呼ばれる特徴が必要になる: 特定のダイジェストを生成するメッセージの探索が計算量的に実現可能であってはいけない。

この要件をハッシュ関数が満たすには、その出力 (ダイジェスト) が非常にランダムに分布する必要がある。例えばダイジェストが 128 ビットでランダムに分布しているとき、特定のダイジェストを生成するメッセージを見つけるには平均で 2¹²⁷ 個のメッセージを試す必要がある。仮にハッシュ関数の出力がランダムに分布していない (つまり、出力されやすい値が存在する) と、一部のメッセージに対しては同じダイジェストを生成するメッセージを簡単に見つけられてしまい、アルゴリズムのセキュリティが損なわれる。なお、ダイジェストの衝突 ── 同じダイジェストを生成する二つのメッセージ ── を見つけるだけであれば、意外にも平均で 2⁶⁴ 個のメッセージを試すだけで済む。この驚くべき事実を使った攻撃は誕生日攻撃 (birthday attack) と呼ばれる。

長年にわたって広く使われている暗号学的ハッシュ関数はいくつか存在する。例えば MD5 (Message Digest 5) や SHA (Secure Hash Algorithm) ファミリーなどがある。MD5 と初期の SHA は脆弱性を持つことが以前から知られており、これを受けて NIST は 2015 年から SHA-3 の利用を推奨している。

メッセージダイジェストの暗号化では、公開鍵と私有鍵を入れ替えて利用できる公開鍵暗号または秘密鍵暗号を利用できる。前者の場合、ダイジェストは送信者の私有鍵 (通常の機密通信では復号で用いる方の鍵) で暗号化され、受信者は送信者の公開鍵で復号を行う。なおこのとき、暗号化されたダイジェストの復号は送信者の公開鍵を知っている任意の主体が行える。

公開鍵と私有鍵を入れ替えて利用できる公開鍵暗号 (の私有鍵) で暗号化されたダイジェストは手書きの署名と同様に否認防止 (non-repudiation) の役目を果たすので、電子署名 (digital signature) と呼ばれる。デジタル署名の付いたメッセージの受信者は、そのメッセージが本当に送信者とされる主体によって署名されたことを送信者の公開鍵を使って誰に対してでも独自に証明できる (秘密鍵暗号では送信者と受信者だけが鍵を知っているので、秘密鍵暗号で暗号化したダイジェストはデジタル署名にならない。それどころか、受信者がメッセージを自作した可能性を否定できない)。上述した性質を持つ任意の公開鍵暗号はデジタル署名に利用できる。DSS (Digital Signature Standard) は NIST が策定したデジタル署名フォーマットであり、公開鍵暗号の選択肢として次の三つを採用する:

1. RSA
2. ElGamal
3. 楕円曲線デジタル署名アルゴリズム (Elliptic Curve Digital Signature Algorithm)

認証子の異なる生成方法として、ダイジェストを暗号化するのではなく、送信者と受信者だけが知っている秘密の値をダイジェストとは別に入力として受け取るハッシュ風の関数を使う方法がある。この様子を 図 199 (a) に示す。こういった関数によって生成される認証子を MAC (message authentication code, メッセージ認証符号) と呼ぶ。送信者は平文に MAC を付け足して送信し、受信者は秘密の値と受け取った平文から計算した MAC が受け取った MAC と一致するかどうかを確認する。

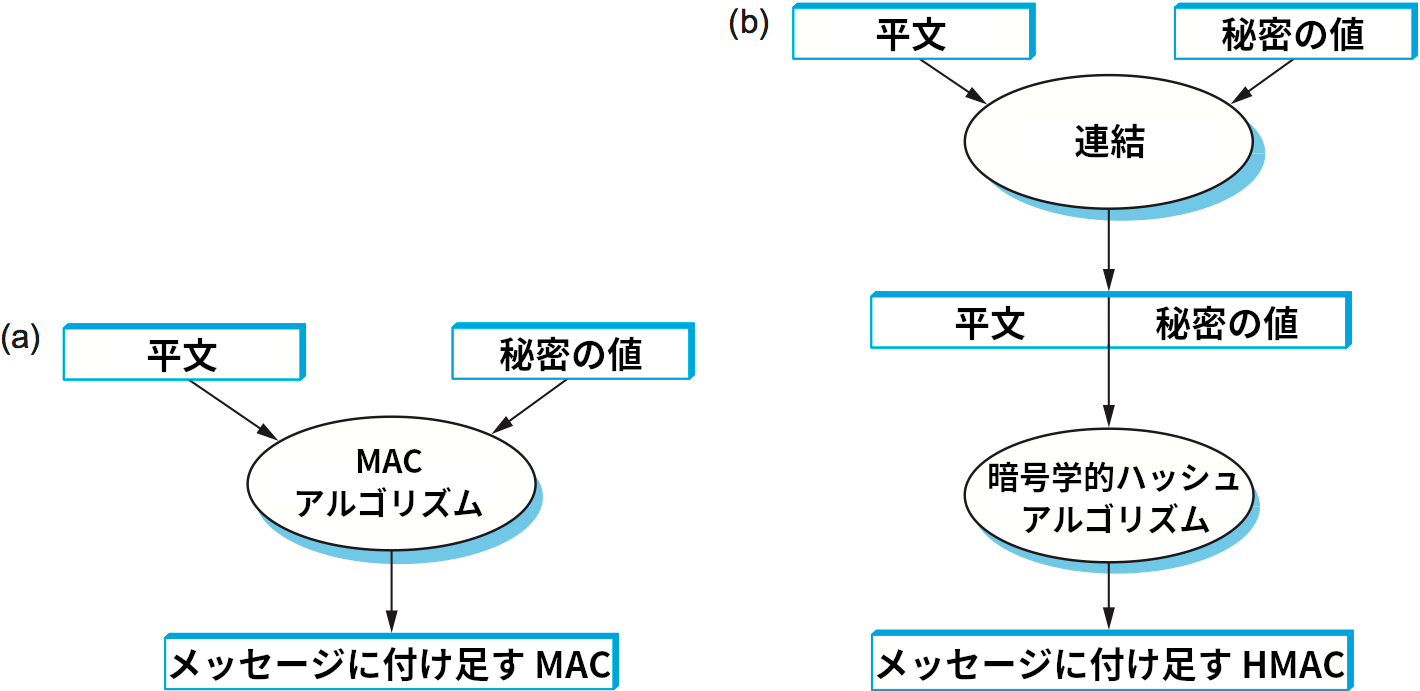
広く使われる MAC の変種として、平文と秘密の値を連結したものに暗号学的ハッシュ関数 (MD5 や SHA-1) を適用して計算する方法がある。こうして計算される値は MAC と同じように扱えるので、HMAC (hashed message authentication code) と呼ばれる。送信される平文には HMAC だけが付け足され、秘密の値は付け足されない。秘密の値を知っている受信者だけが正しい HMAC を計算し、それを受け取った HMAC と比較できる。HMAC を計算するハッシュ関数が一方向性を持たないと、攻撃者は盗聴で得た HMAC の値を生成するハッシュ関数への入力を探索し、見つけた入力を盗聴で得た平文と比較することで秘密の値を見つけられてしまう。

ここまで本節では、メッセージは機密でないと仮定してメッセージを平文のまま送信するものとしてきた。認証子を伴うメッセージに機密性を提供するには、平文と認証子 (MAC、HMAC、または暗号化されたダイジェスト) をまとめて一つのメッセージとして暗号化するだけで済む。なお前述したように、公開鍵暗号よりも秘密鍵暗号の方が格段に高速なので、実際のシステムでは秘密鍵暗号によって機密性が提供されることに注意してほしい。また、セキュリティを強化するために認証子を追加で暗号化したとしてもコストはほとんど増加しない点も指摘しておく。なお、メッセージと (生の) ダイジェストをまとめて暗号化するように単純化した方式もよく用いられる。この方式ではダイジェストが一度だけ暗号化され、暗号文全体が認証子とみなされる。

認証子によって認証の問題は解決されたと思うかもしれない。しかし以降の節を読めば、認証子は問題を解決するシステムの基礎でしかないことが理解できるだろう。まずは、そもそも参加者は鍵をどこから入手するのかという問題を考える。