8.3 鍵の事前配布

暗号と認証子を使うには、通信を行う参加者が通信で用いられる鍵を知っておく必要がある。秘密鍵暗号を使うとき、両参加者は共通の鍵をどのように入手するのだろうか？あるいは公開鍵暗号を使うとき、両参加者は特定の公開鍵が特定の参加者の公開鍵であることをどうやって知るのだろうか？この問題に対する解決策は、鍵が短い間だけ利用されるセッション鍵 (session key) なのか、それとも長い間利用される事前配布鍵 (predistributed key) なのかによって変化する。

セッション鍵とは比較的短い単一の通信をセキュアにするために用いられる鍵を言う。同じ参加者を結ぶ通信であっても、通信 (セッション) のたびに新しいセッション鍵が生成される。セッション鍵を使うとき、通信の暗号化は速度を優先するために秘密鍵暗号で行われる。参加者が通信で用いるセッション鍵を決めるとき、何らかのプロトコル ── セッション鍵生成プロトコル ── が必要となる。セッション鍵生成プロトコル自体にもセキュリティが必要であり (例えば攻撃者が新しいセッション鍵を盗めてはならず)、そのセキュリティは長い間利用される事前配布鍵を利用して提供される。

セッション鍵と事前配布鍵を分ける主な動機は次の二つである:

鍵が利用される時間を短くすると、大量の計算を行う攻撃が成功する確率が減少し、暗号解読者に伝わる暗号文が減り、暗号が突破された場合に流出する情報が減る。
一般に公開鍵暗号は認証とセッション鍵の生成には適しているものの、実行が遅いのでメッセージ全体に機密性を提供する用途には使えない。

本節では最初に事前配布鍵がどのように配布されるかを説明し、その次にセッション鍵がどのように生成されるかを説明する。これからは暗号学の文献でよくあるように通信を行う二人の参加者を「アリス」と「ボブ」と呼ぶ。通信主体を人名で呼びはするものの、実際に通信を行うのはクライアントやサーバーといったソフトウェアあるいはハードウェアであり、現実の特定の人間とは直接的な関係が無い場合も多いことには注意してほしい。

8.3.1 公開鍵の事前配布

公開鍵暗号の公開鍵と私有鍵の組を生成するアルゴリズムは公開されており、実際に鍵の組を生成するソフトウェアは誰でも利用できる。そのため、公開鍵暗号を使いたいと思ったアリスは自分用の公開鍵と私有鍵を生成し、私有鍵は隠しつつ公開鍵を公開する。しかし、公開鍵が本当にアリスのものだと誰でも確信できる形で公開するにはどうするべきだろうか？メールやウェブサイトは利用できない: 攻撃者は「アリスの公開鍵は X です」と主張する偽のメールやウェブサイトを作成できてしまう。このとき、第三者からはアリスと攻撃者が同程度にもっともらしく見える。

公開鍵とアイデンティティの関連付け ── どの鍵が誰のものか ── を証明する完全な仕組みは PKI (public key infrastructure, 公開鍵基盤) と呼ばれる。PKI はアイデンティティの検証とそれに対する公開鍵の関連付けを「アウトオブバンド」に行うところから始まる。ここで「アウトオブバンド」とは、ネットワークとそれを構成するコンピューターと無関係な方法で関連付けを作成することを意味する。例えばアリスとボブが人間なら、アリスはボブと直接会って公開鍵を直接ボブに伝えることができる。あるいはボブが組織でアリスが人間なら、アリスは写真や指紋などからなる伝統的な身元確認書類と共に公開鍵を提出するかもしれない。アリスとボブが同じ企業の所有するコンピューターなら、システム管理者がアリスの公開鍵をボブに教えるだろう。

アウトオブバンドな関連付けはスケールしないと思うかもしれない。確かにその通りだが、これは PKI をブートストラップするために必要になる。最初にアウトオブバンドな関連付けを行えば、後はデジタル署名と信頼の概念を使ってその知識をスケーラブルに広めることができる。例えば、あなたがボブの公開鍵をアウトオブバンドに受け取っていて、公開鍵とアイデンティティの関連付けに関してボブを信頼しているとしよう。このとき、ボブが「アリスの鍵は X です」と記したメッセージをあなたに送信すれば、あなたは (ボブの公開鍵を知っているので) そのメールがボブから送信されたと認証できる。加えてあなたはボブが真実を伝えると信頼しているので、アリスとは会ったこともメッセージを交換したこともないにもかかわらず、あなたはアリスの鍵が X だと確信できる。

デジタル署名を用いれば、ボブはメッセージを送信する必要さえない: 「アリスの鍵は X です」と記したデジタル署名付きの文書をどこかに公開すれば、それだけでボブの公開鍵を知っていてボブを信頼する主体にアリスの公開鍵を確実に伝えられる。こういったデジタル署名付きの公開鍵の公開文書を公開鍵証明書 (public key certificate) と呼ぶ (単に「証明書」とも呼ぶ)。ボブは証明書のコピーをアリスに送ることもできるし、どこかのウェブサイトに掲載することもできる。アリスの公開鍵を検証する必要が生じた主体は、どこからか証明書のコピーを入手し、それをボブの公開鍵を使って認証することで検証を行える ── ただしボブを信頼することが条件となる。これを続ければ、非常に少ない数の鍵 (この例ではボブの鍵だけ) から信頼できる鍵の大きな集合を構築できる。この例でボブの果たす役割を CA (certification authority または certificate authority, 認証局) と呼ぶ。現在のインターネットのセキュリティは様々な CA に依存している側面が大きい。よく知られた商用 CA として VeriSign がある。認証局の話題にはまた後で触れる。

広く使われる証明書の規格に X.509 がある。この規格は証明書の基礎的な構造だけを規定し、詳細の多くを未既定とする。明らかに、証明書は次の要素を含まなければならない:

証明される主体のアイデンティティ
証明される主体の公開鍵
署名者のアイデンティティ
電子署名
デジタル署名アルゴリズムの識別子 (暗号学的ハッシュと暗号の種類)

この他の省略可能な要素としては証明書の有効期限などが考えられる。証明書の有効期限の用途は後述する。

証明書がアイデンティティと公開鍵を関連付ける方法が説明できたので、続いて先ほどから使っている「アイデンティティ」という言葉の意味を考えよう。仮に、証明書に「John Smith の公開鍵は X です」と書かれていたとすれば、その証明書は世界に数千人はいるであろう John Smith 氏のどれを指すのかを特定していないので役に立たない。そのため、証明書は証明されるアイデンティティの名前空間を上手く定義する必要がある。例えば、証明書はメールアドレスや DNS ドメインに対して発行される場合が多い。

PKI が信頼の概念を形式化するときに用いられる方式はいくつか存在する。ここでは二つの重要なアプローチを議論する。

信頼の鎖

この信頼のモデルでは、信頼がバイナリ二値になる: あなたは誰かを完全に信じるか、そうでなければ全く信じない。このとき、複数の証明書によって信頼の鎖 (charin of trust) が構成される。例えば X が Y の公開鍵を証明し、Y が Z の公開鍵を証明するなら、たとえ X と Z が直接会ったことがなくても、X から Z までの信頼の鎖が生まれる。このとき、X の公開鍵を知っている (そして X と Y を信頼する) 人物は Y による Z の公開鍵の証明を信頼できる。言い換えれば、必要なのは信頼できる主体によって署名された証明書の連なりだけであり、その先頭の主体の公開鍵さえ知っていれば以降の公開鍵を全て信頼できる。

先ほど述べたように、アイデンティティの検証と公開鍵証明書の発行を行う信頼できる (とみなされる) 主体を CA (認証局) と呼ぶ。商用 CA や政府機関による CA、そして現在では無料の CA さえ存在する。新しい CA を使うには、その CA の公開鍵を知る必要がある。既に公開鍵を知っている CA による証明書から始まって新しい CA の証明書に至る証明書の連なりがあれば、直接やり取りをせずとも新しい CA の公開鍵を知ることができる。そうして新しい CA の公開鍵が分かれば、その CA が署名する全ての証明書も信じられるようになる。

証明書の集合を図 200 のように木の形をした階層構造にまとめる手法がよく使われる。一番上にあるルート CA の公開鍵を全員が知っておくものとすれば、任意の参加者はルート CA から自身に至る証明書の鎖を他の参加者に示すことができ、その証明書の鎖を示された相手は対応する信頼の鎖を必ず構築できる。

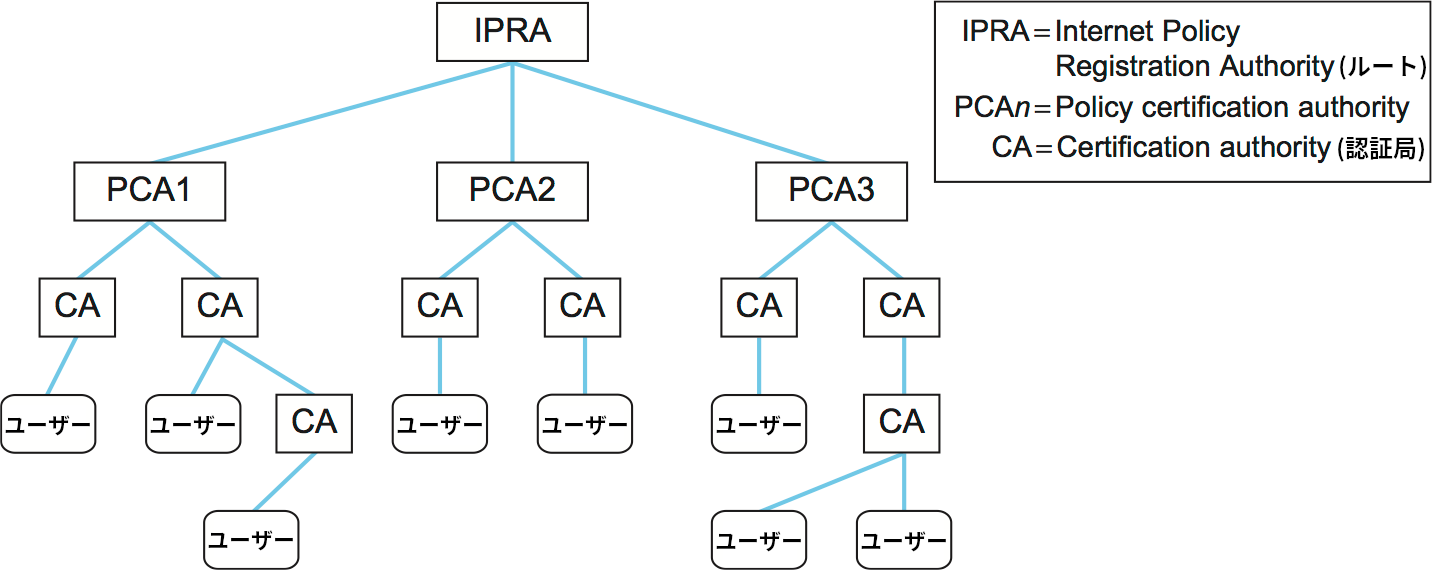
信頼の鎖を構築するアプローチには重大な問題がいくつかある。最も重大なのは、仮にルート CA の正しい公開鍵を知っていたとしても、信頼の鎖を構成する証明書を発行した全ての CA が適切に証明書を発行したことを確認しなければならない点である。アイデンティティを検証せずに証明書を発行する CA が一つでもあれば、それ以外の箇所に問題が無くても信頼の鎖は効力を失う。例えば、ルート CA が第二層 CA の証明書を発行するときに徹底的な検証を行ったにもかかわらず、その第二層 CA が要求を受けた全ての主体に対してアイデンティティを検証せずに証明書を販売する場合などが考えられる。この問題は信頼の鎖が長くなるとそれだけ深刻になる。X.509 証明書には証明対象の主体から伸びる信頼の鎖の長さに制限をかけるためのオプションが存在し、証明書の署名者は証明対象に対する信頼度に応じて許される信頼の鎖の長さを調整できる。

証明書が構成する木構造にはルートが複数あっても構わない。複数のルートが存在する構造は現在のウェブトランザクションのセキュア化で一般的である。例えば Firefox や Internet Explorer といったウェブブラウザにはいくつかの CA に対する証明書が付属する。これは事実上、ブラウザの作成者がそれらの CA と公開鍵は信頼できると判断したのに等しい。ブラウザに信頼させる CA をユーザーが追加することもできる。これらの証明書は SSL/TLS (Secure Socket Layer/Transport Layer Security) で用いられる。SSL/TLS はセキュアなウェブトランザクションで最もよく使われるプロトコルであり、第 8.5 節で詳しく解説される。興味のある読者はブラウザの設定画面から「証明書を見る」といったタブを探し、信頼するように設定されている CA を確認してみるとよい。

信頼の輪

もう一つの信頼モデルは信頼の輪 (web of trust)と呼ばれる。このモデルを採用するソフトウェアの代表例として PGP (Pretty Good Privacy) がある。メール用のセキュリティシステムである PGP ではメールアドレスが公開鍵に対応するアイデンティティとなり、署名はメールアドレスによって行われる。政府機関などの介入から PGP を保護するため、PGP は CA を持たない。その代わり、PGP では誰をどれだけ信頼するかを各個人が判断する ── このモデルでは、信頼が程度の問題となる。加えて、PGP の公開鍵証明書には署名者が証明する公開鍵に抱いている信頼度を表す値が含まれ、ユーザーはいくつかの証明書を集めて自信を高めてから公開鍵を信頼するようにできる。

例えば、アリスが署名したボブの PGP 公開鍵証明書をあなたが手にしたとしよう。あなたはアリスをあまり信頼しておらず、そのままではアリスの証明書が提示するボブの公開鍵を信頼できないとする。この場合でも、アリスと同程度に信頼している別の人物が署名したボブの PGP 公開鍵証明書を入手できれば (そしてボブの公開鍵が一致すれば)、あなたはボブの公開鍵を信頼できるようになるかもしれない。つまり、PGP ではユーザーに生の判断材料を提供されるために信頼の構築という問題が個人で解決できる問題になり、複数の CA からなる単一の階層構造を信頼する必要が生じない。PGP の開発者 Phil Zimmerman の言葉を借りれば、PGP は「自分のパラシュートを自分で袋詰めしたい人」のためにある。

PGP はネットワーキングコミュニティで非常に人気があり、IETF 会合などのネットワーキング関連のイベントでは PGP の鍵署名パーティがよく開催される。そういった集まりで、各参加者は次のことを行う:

アイデンティティを知っている人物から公開鍵を入手する。
自身の公開鍵を他人に伝える。
自身の公開鍵を他人に署名してもらうことで、自身の公開鍵に対する証明書の集合がより多くの人に対して説得力を持つようにする。
他の参加者の公開鍵に署名することで、参加者が公開鍵を配布するときに利用できる証明書の集合を構築するのを助ける。
公開鍵の署名に関して十分信頼できる他の参加者が配布している証明書をもらう。

これを続けると、いずれユーザーは様々な信頼度を持った証明書の集合を保持することになる。

証明書の失効

証明書にまつわる問題として、証明書の失効 (取り消し) がある。なぜこれが問題なのだろうか？例えば、あなたの私有鍵を誰か (攻撃者) が入手したとしよう。あなたの私有鍵に対応する公開鍵の所有者があなたであると記された公開鍵証明書は世界中に無数に存在するので、あなたの私有鍵を手に入れた攻撃者は正当な証明書と私有鍵を使ってあなたに完全になりすますことができてしまう。この問題を解決するには、流出した鍵をあなたのアイデンティティに関連付ける証明書を失効させる機能が必要となる。証明書が失効されれば、その時点で攻撃者はなりすましが行えなくなる。

この問題に対する基本的な解決策は非常に簡単で、各 CA が CRL (certificate revocation list, 証明書失効リスト) と呼ばれる失効した証明書を記したデジタル署名付きリストを発行する。CRL は定期的に更新され、誰でも閲覧できる状態で公開される。CRL はデジタル署名されるので、そのままウェブサイトに掲載して問題ない。CRL があるとき、ボブの公開鍵証明書を受け取ったアリスは最初に CA が発行する最新の CRL を入手して失効していないかどうかを確認する。

証明書は失効しない限り有効となる。そのため、もし証明書に有効期限が存在しないと (失効した証明書がどこかで使われていない確証がないために) CRL から証明書を一切削除できず、CRL が長くなり続ける。このため、証明書を発行するときは有効期限を付けるのが一般的となっている。証明書に有効期限があれば、それを CRL に掲載する期間にも上限が設けられる: 有効期限が切れた証明書は CRL から削除して問題ない。

8.3.2 秘密鍵の事前配布

アリスが秘密鍵暗号を使ってボブと通信しようと思ったとき、アリスは秘密鍵をそのままボブに送って知らせることはできない。二人の間の通信には暗号化による機密性が提供されず、さらにお互いを認証することもできないためである。公開鍵の場合と同様に、何らかの事前配布スキームが必要になる。次に示す二つの明らかな理由により、秘密鍵は公開鍵より事前配布が難しい:

公開鍵暗号では主体ごとに公開鍵が一つあれば認証と機密性が提供できるのに対して、秘密鍵暗号では通信する主体の組につき一つの秘密鍵が必要になる。主体が \(N\) 個あるとき、最大で \(N(N-1)/2\) 個の秘密鍵を用意しなければならない。
公開鍵と異なり、秘密鍵は秘密にする必要がある。

つまり秘密鍵はたくさん必要な上に、誰でも読める証明書のような仕組みを使えない。

秘密鍵の事前配布では KDC (key distribution center, 鍵配布センター) を利用するアプローチが最もよく使われる。KDC は信頼された主体であり、秘密鍵交換の橋渡しを行う。KDC の存在によって管理すべき秘密鍵は最大でも \(N - 1\) 個となり、一部のアプリケーションではアウトオブバンドな生成が可能な数まで減少する。アリスがボブと通信したいとする。このとき通信自体が KDC を通じて行われるわけではなく、KDC はアリスとボブを認証するプロトコルに参加する ── KDC はアリスとボブから以前に受け取った鍵を使ってセッション鍵を生成し、その後アリスとボブは生成されたセッション鍵を使って直接通信する。このアプローチを採用する広く利用されるシステムとして Kerberos がある。Kerberos については次項で詳しく説明する。ここでは秘密鍵を相手に伝えるもう一つの強力なアプローチを説明する。

8.3.3 Diffie-Hellman 鍵交換

秘密鍵を相手に伝えるもう一つのアプローチは Diffie-Hellman 鍵交換 (Diffie-Hellman key exchange)と呼ばれるプロトコルを利用する。Diffie-Hellman 鍵交換は事前に配布された鍵を利用せずに動作する。アリスとボブの間の通信は盗聴されても構わず、仮に盗聴されたとしてもアリスとボブが利用する秘密鍵を盗聴者が知ることはできない。

Diffie-Hellman 鍵交換は参加者を認証しない。セキュアな通信を通信相手が誰か分からないまま行ってもあまり意味がないので、Diffie-Hellman 鍵交換は何らかの認証手段と共に利用される。Diffie-Hellman 鍵交換の主な用途として、IPsec (IP Security) の中心的要素である IKE (Internet Key Exchange) プロトコルでの利用がある。

Diffie-Hellman 鍵交換というプロトコルは二つのパラメータ \(p\), \(g\) を持つ。\(p\), \(g\) の値は公開され、特定のシステムのユーザー全員が同じ値を使って構わない。これから二つのパラメータの選び方を説明する。まず、\(p\) は素数である必要がある。\(p\) が素数なので、整数 \(x\) を \(p\) で割った余り \(x \bmod p\) は \(1\) から \(p-1\) までの整数値を取る。これらの整数値は乗法の下で群 (group) を構成する。次に、パラメータ \(g\) は \(p\) の原始根 (primitive root) である必要がある。つまり \(1\) から \(p-1\) までの任意の整数 \(n\) に対して、\(n = g^k \bmod p\) となるような整数 \(k\) が存在しなければならない。素数には原始根が必ず存在することが知られている。パラメータ \(g\) は生成元 (generator) と呼ばれることもある。

例えば、\(p\) が \(5\) だったとしよう (実際にはこれよりはるかに大きい素数が使われる)。このとき、生成元 \(g\) として \(2\) を選ぶことができる。なぜなら、次の等式が成り立つからである:

\[ \begin{aligned} 1 &= 2^0 \bmod p \\ 2 &= 2^1 \bmod p \\ 3 &= 2^3 \bmod p \\ 4 &= 2^2 \bmod p \end{aligned} \]

アリスとボブが秘密鍵の共有を望んでいるとする。アリスとボブ、および全ての主体は \(p\) と \(g\) の値を知っている。まず、アリスはプライベートな値 \(a\) をランダムに生成し、ボブもプライベートな値 \(b\) をランダムに生成する。\(a\) と \(b\) はどちらも整数の集合 \(\{1,\ \dots,\ p-1\}\) から取られる。アリスとボブは \(a\), \(b\) に対応する公開用の値 ── 暗号化せずに相手に送る値 ── \(A\), \(B\) をそれぞれ次のように計算する:

\[ \begin{aligned} A &= g^a \bmod p \\ B &= g^b \bmod p \end{aligned} \]

その後アリスとボブはそれぞれ \(A\), \(B\) を相手に送信する。最後に、アリスは次の値を計算する:

\[ B^a = (g^b \bmod p)^a = g^{ab} \bmod p \]

そしてボブは次の値を計算する:

\[ A^b = (g^a \bmod p)^b = g^{ab} \bmod p \]

これでアリスとボブは \(g^{ab} \bmod p\) という共通の値を手にしたので、この値を秘密鍵として利用できる。

このやり取りにおいて、盗聴者は \(p\), \(g\) および \(A = g^a \bmod p\) と \(B = g^b \bmod p\) の値を知ることができる。もし盗聴者が \(a\) あるいは \(b\) の値を特定できれば、アリスとボブが使う秘密鍵の値も簡単に計算できてしまう。しかし \(p\), \(a\), \(b\) が十分大きいとき、これらの盗聴できる値から \(a\) または \(b\) を特定する問題は計算量的に実現不可能であることが知られている。この問題は離散対数問題 (discrete logarithm problem) と呼ばれる。

先ほどの例では \(p = 5\) および \(g = 2\) だった。アリスは \(a = 3\) をランダムに選び、ボブは \(b = 4\) をランダムに選んだとしよう。このとき、アリスとボブの公開用の値 \(A\), \(B\) はそれぞれ次のように計算される:

\[ \begin{aligned} A = g^a = 2^3 \bmod 5 = 3 \\ B = g^b = 2^4 \bmod 5 = 1 \end{aligned} \]

その後アリスとボブは \(A\), \(B\) を交換する。最後にアリスは秘密鍵を次のように計算する:

\[ g^{ab} \bmod p = B^a = (2^b \bmod 5)^3 \bmod 5 = (1)^3 \bmod 5 = 1 \]

同様にボブは次の計算で秘密鍵を計算する:

\[ g^{ba} \bmod p = A^b = (g^a \bmod 5)^4 \bmod 5 = (3)^4 \bmod 5 = 1 \]

こうしてアリスとボブは \(1\) を共通の秘密鍵として使うことに合意する。

Diffie-Hellman 鍵交換には通信相手を認証しないという欠点があり、この欠点を利用すると中間者攻撃 (man-in-the-middle attack) と呼ばれる攻撃が行える。攻撃者であるマロリーがメッセージを横取りできると仮定する。マロリーはアリスとボブを騙すために利用するプライベートな値 \(c\) と \(d\) を生成しておく。アリスとボブのそれぞれが公開用の値を相手に送信するとき、マロリーはそのメッセージを横取りし、自身が生成したプライベートな値で作った公開用の値にすり替える。こうすると、マロリーはアリスとボブの秘密鍵を知ることができ、さらにアリスとボブはマロリーの存在に気付けない。この中間者攻撃の様子を図 201 に示す。

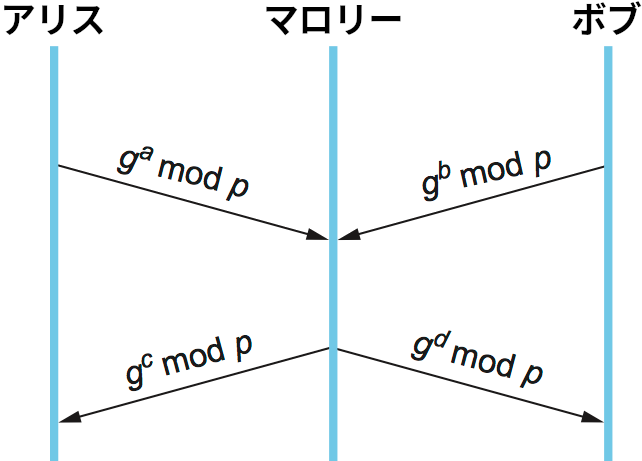
固定 Diffie-Hellman 鍵交換 (fixed Diffie-Hellman key exchange) と呼ばれる Diffie-Hellmann 鍵交換の変種は参加者の片方もしくは両方の認証をサポートする。この方式では公開鍵証明書に似た証明書が利用され、主体の Diffie-Hellman 鍵交換における公開パラメータの証明を通して認証を行う。その証明書には例えば「アリスが利用する \(p\), \(g\), \(g^a \bmod p\) の値は ... です」と書かれている (証明書による認証を利用する場合でも \(a\) の値はアリスだけが知っていることに注意してほしい)。この証明書があると、ボブは鍵を交換している相手がアリスであることを確信できる ── アリス以外の人物は \(a\) の値を知らないので秘密鍵を計算できない。両方の参加者が証明書を持っていれば両者が相手を認証でき、片方の参加者だけが証明書を持っていれば持っていない参加者が持っている参加者を認証できる。後者の機能は一部の状況で有用になる: 例えばウェブサーバーとクライアントがやり取りをするときは、クライアントはクレジットカード番号を送信する前にウェブサーバーを認証してから機密性を持った通信のための秘密鍵を生成するようにできる。