フローとカットの応用

あんなにも高額で、あんなにも最先端の技術を使っているものが、あんなにも役立たずなのはなぜなのか？長い間疑問だったのだが、ふと思ったことがある。コンピューターというのはとても賢いことをする能力を持った馬鹿な機械で、コンピュータープログラマーというのはとても馬鹿なことをする能力を持った賢い人物なのではないかと。つまり、この二つは完璧なタッグなのだ。

――Bill Bryson, Notes from a Big Country (1999)

"鉄のカーテン" が上がって間もない 1990 年、兵器の開発をしていたアメリカ人とロシア人が面会した。アメリカ人は尋ねた「爆弾の開発に必要な膨大な量の計算を、あなたの国の低性能なコンピューターでどうやって行ったのですか？」ロシア人は答えた「良いアルゴリズムを使ったのです」

――Yefim Dinitz, "Dinitz' Algorithm: The Original Version and Even's Version" (2006) より

So I'm the bad guy now I hear, because I don't go with the flow.

Don't ever go with the flow, be the flow.

――Jay-Z, "Stream of Consciousness", May 16, 2015

辺素路

最初に発見された最大フローの応用の一つは、有向グラフ $G$ の特定の頂点 $s$ と $t$ を結ぶ辺素な路集合の大きさの最大値の計算です。ここで $G$ の路の集合が辺素 (edge-disjoint) であるとは、その集合に含まれる路の中に $G$ の任意の辺が最大でも一回しか現れないことを言います。同じ頂点は複数回通っていても構いません。

任意のグラフを考えたとき、辺の重みが全て $1$ ならば、$s$ から $t$ への最大フローは各辺に $0$ または $1$ 単位のフローを流します。フロー分解定理から、飽和した辺を集めた部分グラフ $S$ は互いに素な路または閉路の和として表すことができ、さらに分解に含まれる路の数は最大フローの値と等しいことが分かります。また $S$ から実際の路を取り出すことも簡単です ――$S$ において $s$ から $t$ への適当な路を見つけ、取り除き、再帰すればそれで終わりです。

逆に、互いに素な $k$ 個の $s$ から $t$ への路があれば、それらの路に含まれる辺全てに $1$ 単位のフローを流すことで、値が $k$ のフローを得ることができます。つまり任意の最大フローアルゴリズムは最大フローと同時に最大の辺素路集合も計算していると言えます。

Orlin のアルゴリズムを使って最大フローを計算すれば最大辺素路集合を $O(VE)$ 時間で計算できますが、この単純な応用に Orlin のアルゴリズムを使うというはやりすぎです。実際、カット $(\lbrace s \rbrace, V \backslash \lbrace s \rbrace)$ の容量は最大でも $V - 1$ なので、最大フローの値は最大でも $V - 1$ であり、最初に説明したFord と Fulkerson の増加路アルゴリズムを使ったとしても計算時間は $O(|f^{\ast}| E) = $ $\pmb{O(VE)}$ です。

同じアルゴリズムを使って無向グラフ $G$ の最大辺素路集合を計算することもできます。まず、$G$ に含まれる無向辺 $uv$ を $1$ 単位の容量を持つ二つの有向辺 $u \rightarrow v$ と $v \rightarrow u$ に変更し、この有向グラフを $G^{\prime}$ とします。続いて Ford-Fulkerson のアルゴリズムを使って $G^{\prime}$ の最大フロー $f^{\ast}$ を計算します。もし $f^{\ast}$ が $u \rightarrow v$ と $v \rightarrow u$ の両方を飽和させるなら、両方の辺を削除してもフローの値は変化しません (一般的に言えば、$f^{\ast}$ に含まれる閉路を全て削除して非巡回の最大フローとしてしまっても構いません。ここでは長さが 2 の閉路だけを削除しています)。よって一般性を失うことなく、$f^{\ast}$ が飽和させる辺には一方向にしかフローが流れないと言えます。したがって $f^{\ast}$ が飽和させる有向辺からなる部分グラフを調べれば辺素路集合を取り出せます。

頂点容量と頂点素路

入力グラフ $G$ が辺だけではなく頂点にも容量を持つとします。この設定では関数 $f: E \rightarrow \mathbb{R}_{\geq 0}$ がフローであるための条件に新しい制約が加わります。その制約とは、$s, t$ 以外の全ての頂点 $v$ について $v$ に入るフローの和が非負の定数 $c(v)$ 以下でなければならないというものです (保存条件からこの値は $v$ から出るフローの和と等しくなります): \[ \sum_{u \rightarrow v} f(u \rightarrow v) \leq c(v) \] この新しい制約があったとしても最大フローを計算できるでしょうか？

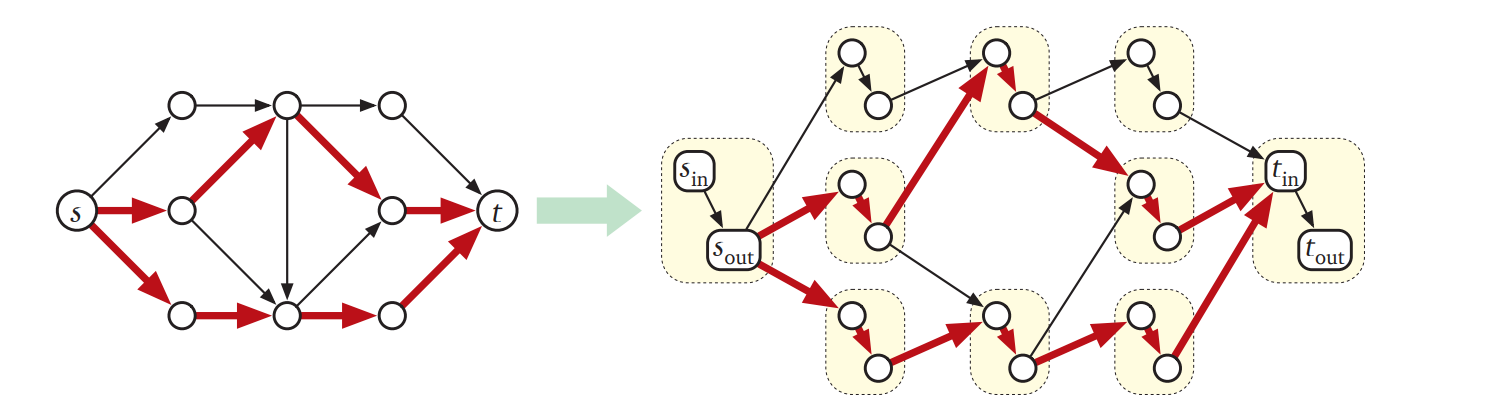
Ford と Fulkerson は 1962 年、この問題を辺だけに容量を持ったグラフ $\tilde{G}$ に帰着させる方法を示しました。ここで $\tilde{G}$ の頂点は $G$ の頂点 $v$ を $v_{\text{in}}$ と $v_{\text{out}}$ に分けた頂点であり、$\tilde{G}$ の辺は全ての $G$ の頂点 $v$ に対する $v_{\text{in}}$ から $v_{\text{out}}$ への容量 $c(v)$ の辺と全ての $G$ の辺 $u \rightarrow v$ に対する容量 $c(u \rightarrow v)$ の $u_{\text{out}} \rightarrow v_{\text{in}}$ という辺です。いつも通り定義を追っていくと、$\tilde{G}$ における任意の実現可能な $(s_{\text{out}}, t_{\text{in}})$-フローに対応する $G$ の実現可能な $(s,t)$-フローが存在し、両者は同じ値を持つことが分かります。つまり、$\tilde{G}$ の最大フローが $G$ の最大フローに対応します。

$G$ から $\tilde{G}$ への帰着には $O(E)$ 時間かかり、その後の $\tilde{G}$ の最大フローの計算には Orlin のアルゴリズムが使えるので、アルゴリズム全体の実行時間は $\pmb{O(VE)}$ です。

ここまでくれば $s$ から $t$ への頂点素路集合の大きさの最大値を求めるのは簡単です: 全ての頂点に $1$ の容量を割り当てて、そのグラフの最大フローを計算すれば良いのです！

図 11.1

$G$ (左) における頂点素路を $\tilde{G}$ (右) における辺素路に帰着させる

二部マッチング

もう一つのよく知られた最大フローの応用は、二部グラフの最大マッチング (maximum matching) の計算です。グラフのマッチングとは全ての頂点の次数が最大でも $1$ であるような部分グラフのことであり、同じ頂点を共有しない辺の集合としても定義できます。ここで考える問題はマッチングであって辺の数が最大のものを計算する問題です。

例えば何人かの医師が職を探していて、いくつかの病院が医師を探しているとしましょう。各医師は働きたい病院をいくつか提示し、各病院は雇いたい医師を何人か提示しているときに、お互いが納得するような医師と病院の雇用関係をなるべく多く作りたいとします¹。この問題は医師と病院を頂点とし、互いに雇用関係を結べる場合に限って辺があるような二部グラフに対する最大マッチングを求める問題と考えることができます。

この問題を最大フローへの帰着を使って解く方法をこれから示します。$G$ を二部グラフとし、頂点集合は $L \cup R$ であって、辺は $L$ にある頂点と $R$ にある頂点を結んでいるとします。このとき $G$ から新しいグラフ $\tilde{G}$ を次のように作成します:

全ての辺を $L$ から $R$ に向き付ける。
新しい頂点 $s$ と $t$ を追加する。
$s$ から $L$ の全ての頂点への辺を追加する。
$t$ から $R$ の全ての頂点への辺を追加する。
全ての辺の重みを $1$ とする。

$G$ の任意のマッチング $M$ は次のようにして $G^{\prime}$ のフロー $f_{M}$ に変形できます: 「全ての $M$ の辺 $uw$ について、$s \rightarrow u \rightarrow w \rightarrow t$ という辺に沿って $1$ 単位のフローを追加する」この処理によって追加される有向路は $s$ と $t$ 以外に点を共有しないので、各頂点における保存条件が満たされます。また $f_{M}$ の値は $M$ に含まれる辺の数と等しくなります。

逆にFord-Fulkerson の増加路アルゴリズムを使って計算した $G^{\prime}$ の $(s,t)$-フローを $f$ とします。辺の容量が整数なことから Ford-Fulkerson のアルゴリズムが辺に割り当てるフローは必ず整数 (再帰法で簡単に示せます。ヒント、ヒント) であり、全ての辺が $1$ 単位の容量を持つことから $f$ は $G^{\prime}$ の辺を飽和させる ($f(e)=1$) か避ける ($f(e) = 0$) かのどちらかです。さらに $L$ の各頂点に入る辺の数および $R$ の各頂点から出る辺の数は最大でも $1$ なので、$L$ から $R$ への飽和した辺全体の集合は $G$ のマッチングとなり、その大きさは $|f|$ です。

以上より $G$ の最大マッチングの大きさは $G^{\prime}$ の最大フローの値と等しいこと、さらに増加路を使って作られた最大フローから $O(E)$ 時間で最大マッチングを計算できることが分かります。よって Orlin のアルゴリズムあるいは単純に Ford-Fulkerson のアルゴリズムを使えば、二部グラフの最大マッチングを $\pmb{O(VE)}$ 時間で計算できます。

図 11.2

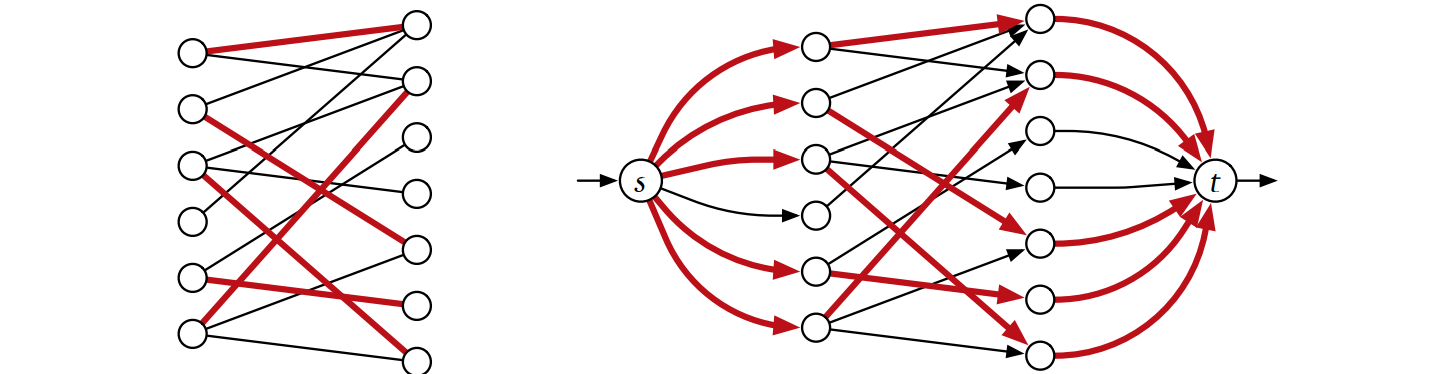
二部グラフ $G$ の最大マッチングとそれに対応する $G^{\prime}$ の最大フロー

Ford-Fulkerson のアルゴリズムを $G^{\prime}$ に対して実行したときの様子を元の二部グラフ $G$ の視点で観察すると、面白いことが分かります。アルゴリズムは $G$ におけるマッチング $M$ を空のマッチングから初めて構成しますが、$M$ における辺は $G^{\prime}$ においてフローが流れている辺に対応します。$M$ の辺に含まれる $G$ の頂点をマッチしていると呼び、そうでない点をマッチしていないと呼ぶことにします。そうするとアルゴリズムの各反復で探索されるのは $G$ における"交互路" ――$L$ のマッチしていない点と $R$ のマッチされていない点を結ぶ辺から始まり、以降は $M$ に属する辺と $M$ に属さない辺が続くような路―― であり、$G$ における交互路が $G^{\prime}$ における増加路に対応します。増加路 $P$ が見つかったならば、$M$ を $P$ との対称差 $M \otimes P$ で更新します。これによって $M$ の大きさは一増え、一回の反復が終了します。もし増加路が無かった場合には、最大フロー最小カット定理から $M$ が最大マッチングであることが分かるので、アルゴリズムは終了します。増加路を見つけるのには $O(E)$ 時間かかり、反復は最大で $V$ 回なので、このアルゴリズム全体の実行時間は $\pmb{O(VE)}$ です。上図にアルゴリズムを実行した様子を示します。

最大二部マッチングの交互路を使った特徴付けは Claude Berge (クロード・ベルジュ) によって 1957 年に (最大フロー最小カット定理とは独立に) 初めて示されました。また似た手続きを含むアルゴリズムは 1955 年には Harold Kuhn (ハロルド・クーン) によって、1916 年には Dénes Kőnig (デニス・ケーニヒ) によって、1836 年には Carl Jacobi (カール・ヤコビ) によってそれぞれ示されています。

1973 年に John Hopcroft (ジョン・ホップクロフト) と Richard Karp (リチャード・カープ) によって提案されたより洗練されたアルゴリズムを使うと、二部グラフの最大マッチングを $O(\sqrt{V}E)$ 時間で計算できます。このアルゴリズムは各反復で互いに交わらない交互路を複数見つけます。

タプル選択

二部グラフの最大マッチングは私がタプル選択 (tuple selection)² と呼ぶ問題クラスの一番簡単な例です。タプル選択問題の入力は要素に重複がない有限集合 $X_{1}, X_{2}, \ldots, X_{d}$ であり、出力は容量に関する次の条件を満たす最大の $d$-タプルの集合です:

全ての添え字 $i$ に対して、各 $x \in X_{i}$ がタプルに現れていいのは $c(x)$ 回まで。
全ての添え字 $i$ に対して、各 $x \in X_{i}$ と $y \in X_{i+1}$ がタプルに現れていいのは $c(x,y)$ 回まで。

上界 $c(x)$ と $c(x,y)$ は (通常は小さな) 非負整数あるいは $\infty$ です。

二部グラフの最大マッチング問題では $d=2$、全ての要素 $x$ について $c(x)=1$ 、全ての組 $(x, y)$ について辺 $xy$ があるなら $c(x,y)=1$ で辺がないなら $c(x,y)=0$ です。

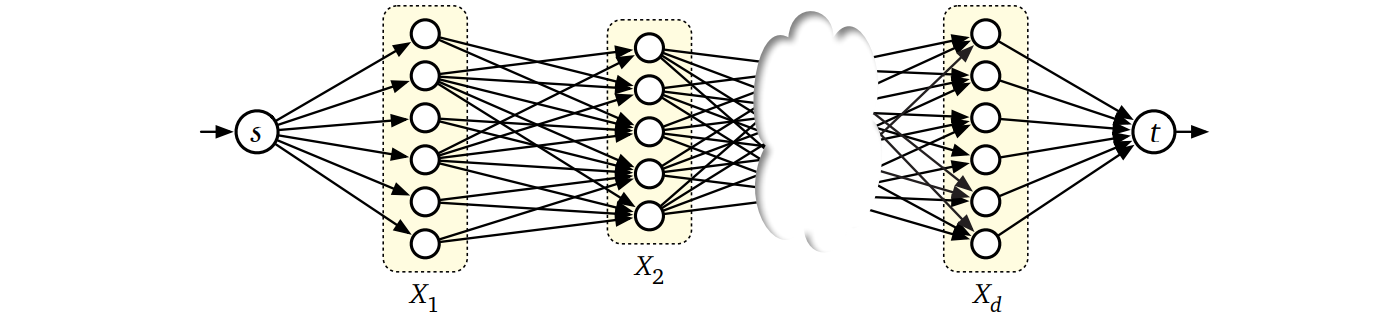
与えられる集合が一列に並んでいて、容量の制約が隣接した集合 $X_{i}$ と $X_{i+1}$ だけを考えること³を利用すれば、タプル選択問題を次のように定義されるグラフ $G$ における最大フロー問題に帰着させることができます:

$G$ には $X_{i}$ の各要素に対応する頂点があり、その他にソース頂点 $s$ とシンク頂点 $t$ がある。$s$ と $t$ を除く各頂点 $x$ は容量 $c(x)$ を持つ。
$G$ には全ての $w \in X_{1}$ に対して容量 $1$ の辺 $s \rightarrow w$ があり、全ての $z \in X_{d}$ に対して容量 $1$ の辺 $z \rightarrow t$ が存在ある。そして全ての添え字 $i$ に対して全ての $x \in X_{i}$ と $y \in X_{i+1}$ の間に容量 $c(x,y)$ の辺 $x \rightarrow y$ がある ($c(x,y)=0$ である辺 $x \rightarrow y$ は存在しないとしてもよい)。

$s$ から $t$ への任意の路は選択可能な $d$-タプルを表します (路がタプルそのものだとも言えます)。逆に制約を満たす $d$-タプルは $G$ における $s$ から $t$ への路を表します (タプルが路そのものだとも言えます)。

より一般的に議論をするために、$G$ における任意の実現可能な $(s,t)$-フローを $f$ とします。容量は整数または $\infty$ なので、フロー分解定理より $f$ は $s$ から $t$ への一単位のフローが流れる路 $|f|$ 個の和として書くことができます。定義を追っていけばこれらの路が表すタプルの集合が容量に関する制約を満たすことが示せます。逆に容量に関する制約を満たす $k$ 個のタプルに対して、対応する路の和は値が $k$ の実現可能な $(s,t)$-フローとなります。

したがって容量に関する制約を満たす最大のタプルの集合は、$G$ の最大フロー $f^{\ast}$ を計算すれば見つけることができます。なぜなら $G$ に含まれる有限の重みが整数であることから一般性を失うことなく $f^{\ast}$ が整数フローであると仮定でき、よって (一つ前の段落から) $f^{\ast}$ は $|f^{\ast}|$ 個の制約を満たすタプルに対応するからです。

試験のスケジューリング

次に説明する "現実世界の" スケジューリング問題を見れば、一般的な帰着をよりよく理解できるかもしれません。

あなたは Sham-PooBanana 大学に雇われて期末試験のスケジュールを立てるアルゴリズムを設計することになりました。$n$ 個の講義の期末試験が行われる時と場所を、 $t$ 個の時間帯と $r$ 個の教室から決めなければなりません。ある時間帯にある教室で行える試験は最大でも一つであり、試験を複数の時間帯・教室に分けて行うことはできません。また各試験には試験監督⁴が一人着く必要があり、試験を監督できる人物は $p$ 人いて、それぞれ監督可能な時間帯が異なっています。またどの試験監督も合計で 5 個より多い試験を監督することはできません。

このスケジューリング問題の入力は三つの配列です:

整数の配列 $E[1..n]$: $E[i]$ が $i$ 番目の講義の試験に出席する学生の数を表す。
整数の配列 $S[1..r]$: $S[j]$ が $j$ 番目の教室の座席数を表す。$i$ 番目の講義の試験が $j$ 番目の教室で行えるのは $E[i] \leq S[j]$ が成り立つときだけ。
真偽値の配列 $A[1..t, 1..p]$: $A[k,l] = \textsc{True}$ は $l$ 番目の試験監督が $k$ 番目の時間帯に試験を監督できることを表す⁵。

$N = n + r + tp$ で入力サイズを表すとします。あなたの仕事は教室、時間帯、試験監督を全ての期末試験に割り当てるか、そのような割り当てが不可能であると正しく報告するアルゴリズムを設計することです。

この問題は典型的なタプル選択問題であり、四つの集合が登場します: 講義、教室、時間帯、そして試験監督の集合です。この問題を解くために、六種類の頂点 ――ソース頂点 $s^{\prime}$, 講義を表す頂点 $c_{i}$, 教室を表す頂点 $r_{j}$, 時間帯を表す頂点 $t_{k}$, 試験監督を表す $p_{l}$, シンク頂点 $t^{\prime}$―― および五種類の辺を持つフローネットワーク $G$ を構築します:

全ての講義 $i$ について容量 $1$ の辺 $s^{\prime} \rightarrow c_{i}$ が存在する (「全ての講義は最大でも一つの期末試験を持つ」)。
教室 $i$ と講義 $j$ が $E[i] \leq S[j]$ を満たすときに限って辺 $c_{i} \rightarrow r_{i}$ が存在し、その容量は $\infty$ である (「講義 $i$ が教室 $j$ で試験を行えるのは教室に十分な席があるときだけ」)。講義の生徒数 $E[i]$ と教室の座席数 $S[j]$ が使われるのはここだけ。
全ての教室 $j$ と時間帯 $k$ に対して容量 $1$ の辺 $r_{j} \rightarrow t_{k}$ が存在する (「教室 $j$ で時間帯 $k$ に行われる試験は最大でも一つ」)。
$A[k,l] = \textsc{True}$ であるような時間帯 $k$ と試験監督 $l$ に対して容量 $1$ の辺 $t_{k} \rightarrow p_{l}$ が存在する (「試験監督は監督可能な時間帯に最大一つの試験を監督できる」)。
全ての試験監督 $l$ に対して容量 5 の辺 $p_{l} \rightarrow t^{\prime}$ が存在する (「試験監督が監督できる試験は最大 5 個」)。

(ソース頂点とシンク頂点を $s^{\prime}, t^{\prime}$ と呼んでいるのは問題文で $t$ が時間帯の数を表すために既に使われているからであり、そうしなければいけない特別な理由はありません) まとめると、$G$ は $n + r + t + p + 2 = O(N)$ 個の頂点と $O(nr + rt + tp) = O(N^{2})$ 個の辺を持ちます。

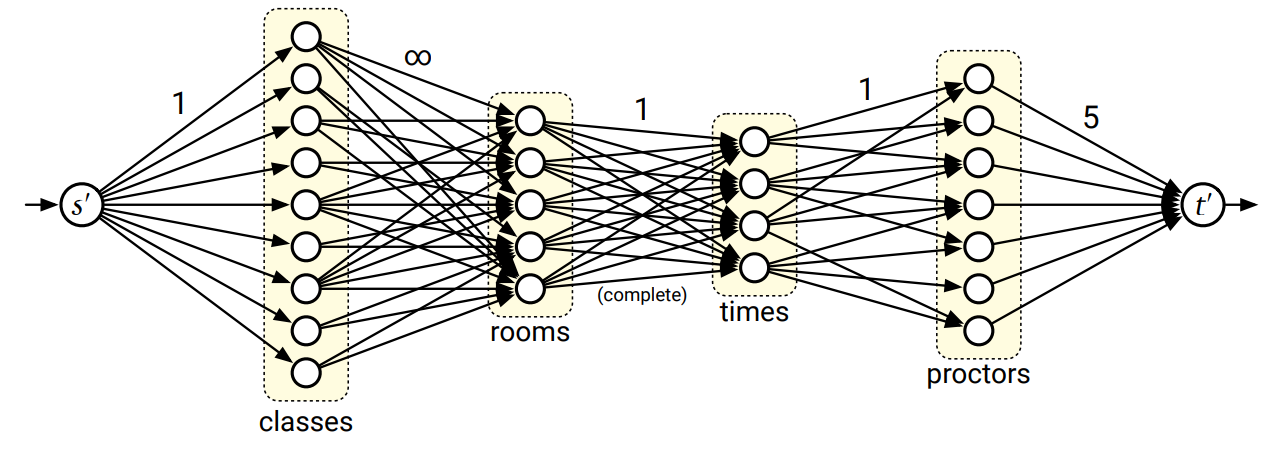
$G$ における $s^{\prime}$ から $t^{\prime}$ への路は、一つの期末試験に対する制約を満たす講義、教室、時間帯、試験監督の組を表します。つまり講義を取っている全ての生徒は教室に収まり、試験監督はその時間帯に試験を監督できるということです。逆に正しい (講義、教室、時間帯、試験監督の) 組には対応する $s^{\prime}$ から $t^{\prime}$ への路が $G$ に存在します。よって行う試験の数を最大化するような制約を満たすスケジュールを構築するには、まず $G$ における最大 $(s^{\prime},t^{\prime})$-フローを計算して、それから最大フローに含まれる路を講義、教室、時間帯、試験監督の組に変換すれば良いことになります。もし $|f^{\ast}| = n$ ならば計算されたスケジュールを返し、そうでなければ $n$ 個の期末試験を行うスケジュールが不可能だと正しく報告します。

入力データから $G$ を総当たりで作るのには $O(E)$ 時間かかり、最大フロー $f^{\ast}$ は $|f^{\ast}| \leq n < V$ を満たすので Ford-Fulkerson のアルゴリズムまたは Orlin のアルゴリズムを使って $O(VE)$ 時間で計算でき、フロー分解は $O(VE)$ 時間で計算できます。したがって、この問題を解くアルゴリズム全体の実行時間は $O(VE) = \pmb{O(N^{3})}$ です。

素路被覆

有向グラフ $G$ の路被覆 (path cover) とは、$G$ の有向路の集合であって $G$ の全ての辺が少なくとも一つの路に含まれるものを言います。$G$ の素路被覆 (disjoint-path cover) とは、$G$ の路被覆であってどの頂点もちょうど一つの路に含まれるものを言います。

任意の有向グラフには長さがゼロの路だけからなる自明な素路被覆がありますが、これは面白くありません。そうではなくて、なるべく少ない路を使った素路被覆を見つける問題を考えましょう。この問題は一般的なグラフに対しては NP 困難です ――有向グラフが大きさが $1$ の素路被覆を持つことはハミルトン路を持つことと同値だからです―― が、有向非巡回グラフに対してはフローを使った効率の良いアルゴリズムが存在します。

与えられた有向非巡回グラフ $G=(V,E)$ の最小素路被覆を求めるには、次に示す新しい二部グラフ $G^{\prime} = (V^{\prime}, E^{\prime})$ を使います:

$G$ の各頂点 $v$ に対して、$G^{\prime}$ には $v^{\flat}$ と $v^{\sharp}$ という頂点がある。
$G$ の各有向辺 $u \rightarrow v$ に対して、$G^{\prime}$ には $u^{\flat}v^{\#}$ という無向辺がある。

($G$ が隣接行列で表されているなら、$G^{\prime}$ は同じ隣接行列で表される二部グラフです！)

図 11.5

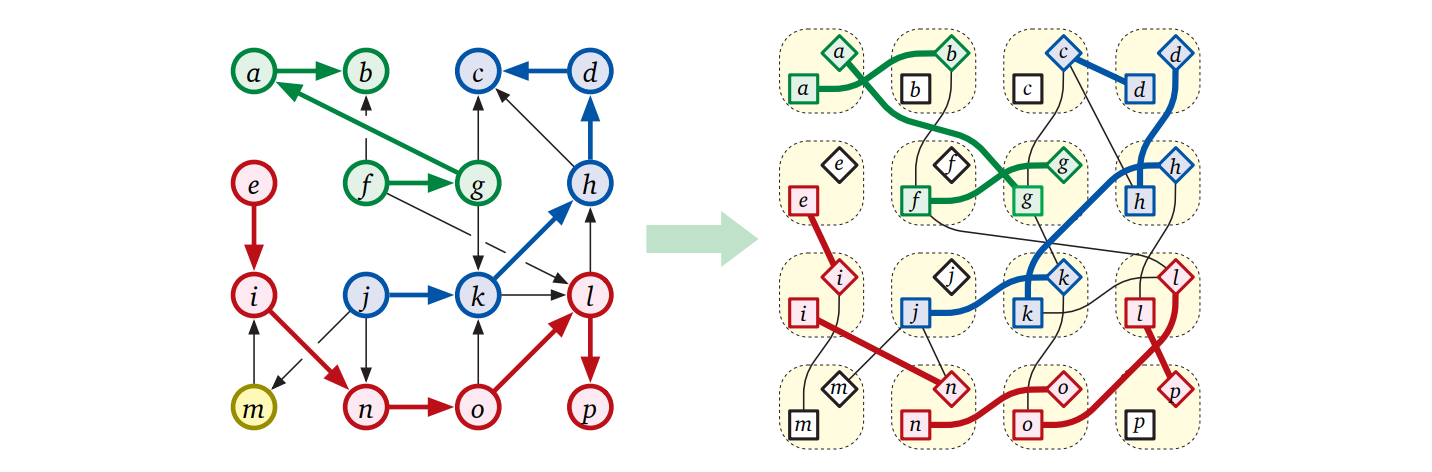
DAG の最小素路被覆を最大二部マッチングに帰着させる (四角がフラット $\flat$、ダイアモンド型がシャープ $\sharp$ を表す)

「$k$ 個の互いに素な路で $G$ を被覆できる」が「$G^{\prime}$ に大きさ $V-k$ のマッチングが存在する」と同値なことをこれから示します。いつも通り、同値性は二つのステージに分けて示します。

$(\Rightarrow)$ $G$ が $k$ 個の互いに素な路からなる被覆 $P$ を持つとする。$P$ を部分グラフとみなすと、$P$ の各頂点の入次数は $0$ か $1$ であり、入次数が $0$ である点は $P$ に含まれる路につき一つずつしか含まれない。よって $P$ に含まれる辺の数は $V - k$ 個である。$G^{\prime}$ の辺の部分集合 $M$ を次のように定義する: \[ M := \lbrace u^{\flat} v^{\sharp} \in E^{\prime}\ |\ u \rightarrow v \in P \rbrace \] $P$ が素路被覆であることから、$G$ の各頂点 $v$ について $v$ から出る辺と $v$ に入る辺はどちらも最大一つであることが分かる。したがって $G^{\prime}$ の各頂点は $M$ において次数が $1$ 以下であり、$M$ は大きさ $V - k$ のマッチングである。
$(\Leftarrow)$ $G^{\prime}$ が大きさ $V - k$ のマッチング $M$ を持つとする。 \[ M^{\prime} := \lbrace u \rightarrow v \in E \ |\ u^{\flat}v^{\sharp} \in M \rbrace \] とし、$P = (V, M^{\prime})$ と置くことで $M$ を $G$ の部分グラフに変換する。マッチングの定義から、$G$ の各頂点は $P$ において外向き辺および内向き辺をそれぞれ最大でも一つしか持たない。よって $P$ は $G$ の互いに素な有向路の集合であり、$P$ が全ての頂点を含むことからこの集合は $V-k$ 個の辺を持つ素路被覆である。$P$ に含まれる路の数は $M^{\prime}$ において向かってくる辺が存在しない $G$ の頂点の数と等しいので、$P$ にはちょうど $k$ 個の路が含まれることが分かる。

以上より $G$ の最小素路被覆を $G^{\prime}$ の最大マッチングを計算することで求められることが直ちに分かります。Ford-Fulkerson の最大フローアルゴリズムを使えば、この計算は $O(V^{\prime} E^{\prime}) =$ $\pmb{O(VE)}$ 時間で行えます。

この問題は DAG と路という言葉を使って定式化されていますが、実際には最大マッチングの問題です。つまり、グラフのなるべく多い頂点を (路における) 後者とマッチさせる問題であるということです。DAG を被覆するために必要な路の数は、前者を持たない頂点の数と同じになります (そしてもちろん、二部グラフの最大マッチング問題は実際には最大フローの問題です)。

教師の最小雇用問題

Sham-PooBanana 大学に戻って、"現実世界" のスケジューリング問題をもう一つ見ましょう⁶。SPU では毎日数千の講義が開かれているのですが、予算の大幅な削減によって学部のサイズを大きく減らす必要が生じました。しかし生徒は既に学費を払っているために (そして大学には弁護士を雇うお金もないために)、講義カタログに載っている講義を全て開講できるだけの教授を残しておかなければなりません。残しておかなくてはいけない SPU の教授は最低で何人でしょうか？

残された学部の教授には曜日ごとに講義が割り当てられます。各教授に割り当てられる講義の時間は重なってはならず、さらに講義と講義の間には教室を移動するための空き時間が必要になります。問題を簡単にするために、全ての教授は全ての講義を教えることができ、さらにオフィスアワーも昼食休憩もトイレ休憩も取らないとしましょう⁷。

きちんと述べると、$n$ 個の講義が $m$ 箇所で開講されるときの問題の入力は次のデータです:

講義を表す配列 $C[1..n]$: $C[i]$ には三つのフィールドがあり、それぞれ開始時間 $C[i].\mathit{start}$ と終了時間 $C[i].\mathit{end}$ と教室の場所 $C[i].\mathit{loc}$ である。
二次元配列 $T[1..m, 1..m]$: $T[u,v]$ が教室 $u$ から教室 $v$ へ移動するのにかかる時間を表す。

計算するのは全ての講義を開講するために必要な教授の数の最小値です。各教授に $C[i]$ と $c[j]$ が割り当てられ $C[j].\mathit{start} \geq C[i].\mathit{start}$ であるとすれば、 \[ C[j].\mathit{start} \geq C[i].\mathit{end} + T[C[i].\mathit{loc}, C[j].\mathit{loc}] \] が満たされる必要があります。

この問題は素路被覆への帰着を使って解くことができます。素路被覆問題への入力は DAG $G=(V,E)$ であり、$G$ の頂点が講義を表し、二つの講義の間に辺があるのは時間帯が十分離れているために同じ教授が両方を担当できるときであるようなグラフとします。つまり有向辺 $i \rightarrow j$ は同じ教授が講義 $i$ と講義 $j$ の両方を担当できることを示すということです。総当たりを使えばこのグラフを $O(n^{2})$ 時間で簡単に構築できます。

$G$ の素路被覆を前述のマッチングアルゴリズムを使って計算すれば、被覆に含まれる $G$ の有向路がある一人の教授に対する講義スケジュールを表します。アルゴリズム全体の実行時間は $O(n^{2} + VE) = \pmb{O(n^{3})}$ です⁸。

問題文では区間と距離という言葉が使われていたこの問題は、実際には最大マッチングの問題 (したがって最大フローの問題) であることが分かりました。つまり、できるだけ多くの講義を、同じ教授が担当する次の講義とマッチさせる問題であるということです。必要となる教授の数は次の講義が存在しない講義の数と等しくなります: そのような講義はある教授が担当する最後の講義です。

ペナントレースにおける敗退

毎年何百万人という野球ファンが熱心に試合を観戦し、贔屓チームがプレーオフそしてワールドシリーズに進むことを期待します。しかし非情なことに、シーズンが終わる数日前あるいは数週間前の時点で、ほとんどのチームはペナントレースから "数学的に" 敗退します。通常はあるチームが敗退したかどうかを判断するのは簡単です ――現在地区トップのチームに追いつけるほど試合数が無ければ敗退です―― が、状況がもっと複雑になることもあります。次に示すのは 1996 年 8月 30 日のアメリカンリーグ東地区で実際に起こった順位です: \[ \begin{array}{ccc|ccccc} \hline \text{チーム} & \text{勝-敗} & \text{残り試合数} & \text{NYY} & \text{BAL} & \text{BOS} & \text{TOR} & \text{DET} \\ \hline \text{New York Yankees} & 75-59 & 28 & & 3 & 8 & 7 & 3 \\ \text{Boltimore Orioles} & 71-63 & 28 & 3 & & 2 & 7 & 4 \\ \text{Boston Red Sox} & 69-66 & 27 & 8 & 2 & & 0 & 0 \\ \text{Toronto Blue Jays} & 63-72 & 27 & 7 & 7 & 0 & & 0 \\ \text{Detroit Tigers} & 49-86 & 27 & 3 & 4 & 0 & 0 & \\ \hline \end{array} \] 明らかに Detroit は後れを取っていますが、それでも粘り強いファンは希望を捨てていませんでした。もし Detroit が残りの 27 試合に全て勝利すれば合計で 76 勝となって現在のどのチームよりも勝利数が多くなるからです。その上で他のチームが全ての試合に敗北すれば...。

しかし他のチームもお互いに試合をしなければならないので、これは不可能です。理由を完全に説明すると次のようになります⁹:

残りの試合全ての勝利することで、Detroit はシーズンを 76 勝 86 敗という成績でシーズンを終えることができる。しかし Yankees が 2 試合でも勝利すれば 77 勝 85 敗となって Detroit を上回る成績となる。よって Tigers が一度も負けずに、Yankees が一度も勝てずにシーズンが終わると仮定する。

このシナリオにおける問題は、New York が Boston との試合を 8 試合残しているという点にある。Red Sox がそれらの試合に全て勝利した場合、77 勝以上が確定して Tigers よりも良い成績となってしまう。よって Detroit が一位となる可能性を消さないためには、New York が Boston との 8 試合のうちちょうど $1$ 試合だけ勝利し、他の試合に敗北する必要がある。一方で Sox は New York 以外との全ての試合において敗北しなければならない。以上の条件が成り立てば、Detroit と New York と Red Sox が同着一位となる ...。

このシナリオにおいて Orioles と Blue Jays で何が起こるかを見よう。Baltimore は Boston と 2 試合、New York と 3 試合が残っているので、上記のようにことが進んだ場合には Baltimore は最低でも 76 勝でシーズンを終えることになる。よって Detroit が Baltimore に抜かされないためには、Baltimore は New York と Boston 以外の全ての試合に敗北しなければならない。つまり、Baltimore は Totonto との残り 7 試合全てに敗北しなければならない。一方で Blue Jays は Yankees との試合も 7 試合残っており、既に見た通り Detroit が一位となるためにはこの試合は全て Blue Jays が勝利する必要がある。しかしそうなると Blue Jays は現在の状況から 14 試合に勝利することになり、最終成績が 77 勝となって Detroit を抜いて一位となってしまう。したがって、これから何が起ころうとこのシーズンにおいて Detroit がアメリカンリーグ東地区で一位になることは不可能である。

もっと簡単にこれを示す方法があるはずです！

この問題を抽象的に定式化するとこうなります: 入力は二つの配列 $W[1..n]$ と $G[1..n,1..n]$ であり、$W[i]$ がチーム $i$ の現在の勝利数を表し、$G[i,j]$ がチーム $i$ とチーム $j$ の残り試合数を表します。出力はチーム $n$ が最多の勝利数でシーズンを終えることができるかどうかです (同着一位でも良いとします)¹⁰。

1960 年代の中頃、Benjamin Schwartz (ベンジャミン・シュワルツ) はこの問題が最大フローを使ってモデル化できることを示しました。それから約 20 年後、Dan Gusfield (ダン・ガスフィールド)、Charles Martel (チャールズ・マーテル)、David Fernández-Baca (デイビッド・フランシス・バカ) は Schwartz のフローによる定式化を組選択問題に単純化しました。つまり、チーム $n$ が一位となるための各ゲームにおける勝者を選択するということです。$R[i] = \sum_{j} G[i,j]$ をチーム $i$ の残り試合数とし、これ以降はチーム $n$ が残りの $R[n]$ 試合に全て勝利すると仮定します。この仮定の下でチーム $n$ が一位になれるのは、他の全てのチーム $i$ について、残り $R[i]$ 試合における勝利数が $W[n] + R[n] - W[i]$ 以下であるときだけです。

各試合で勝利するチームを選択することから、頂点が試合とチームを表す二部グラフを構築します。試合を表す $\binom{n}{2}$ 個の頂点 $g_{i, j}$ $(1 \leq i < j < n)$ とチームを表す頂点 $t_{i}$ $(1 \leq i < n)$ を考え、全ての添え字の組 $(i,j)$ について、容量が無限大の $g_{i,j} \rightarrow t_{j}$ と $g_{i,j} \rightarrow t_{i}$ という辺を追加します。さらにソース頂点 $s$ と各組 $(i,j)$ に対する容量 $G[i,j]$ の辺 $s \rightarrow g_{i,j}$ を追加し、シンク頂点 $t$ と各チーム $i$ に対する容量 $W[n] + R[n] - W[i]$ の辺 $t_{i} \rightarrow t$ も加えます。

1996年のアメリカンリーグ東地区に対するグラフを次に示します。チーム $n$ は Detroit Tigers で、ラベルの付いていない辺は無限大の容量を持ちます。

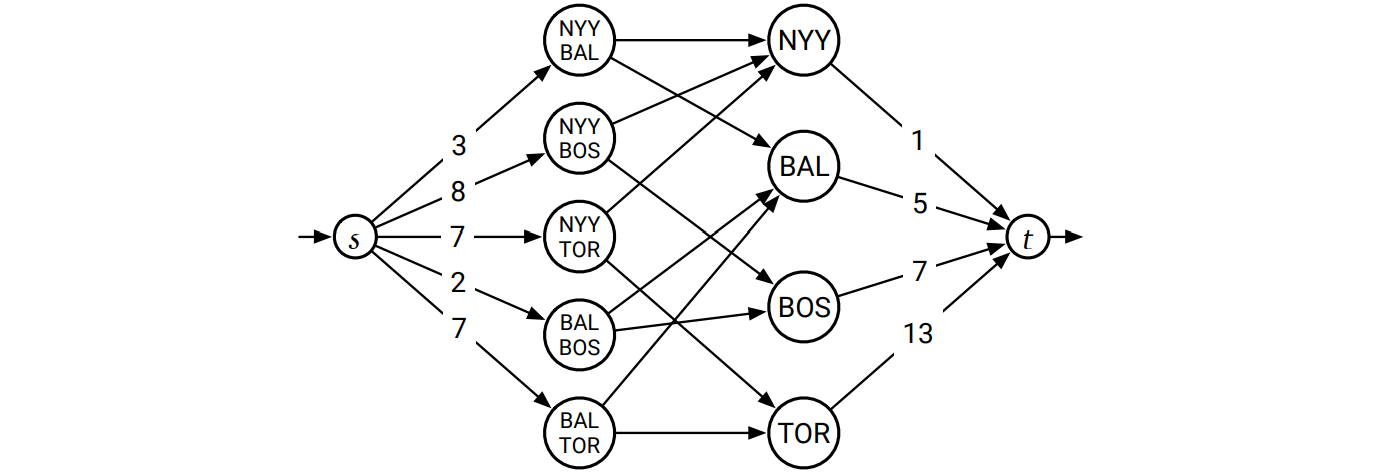
定理チーム $n$ が一位でシーズンを終えられることは、$s$ から出る全ての辺を飽和させる実現可能なフローが存在することと同値。

証明チーム $n$ が一位でシーズンを終えられるとする。このとき他の全てのチーム $i < n$ の残り試合における勝利数は最大でも $W[n] + R[n] - W[i]$ である。チーム $n$ が一位となるシナリオにおいて、$i$ と $j$ が戦って $k \in \lbrace i, j \rbrace$ が勝つような試合ごとに有向路 $s \rightarrow g_{i,j} \rightarrow t_{k} \rightarrow t$ に沿って一単位のフローを流していく。$i$ と $j$ の間の試合は $G[i,j]$ 回行われるので、こうして出来上がるフローは $s$ から出る全ての辺を飽和させる。また各チーム $i$ の勝利数は最大でも $W[n] + R[n] - W[i]$ だから、こうして出来上がるフローは実現可能である。

逆に $s$ から出る全ての辺を飽和させる実現可能なフロー $f$ が存在するとする。このとき全ての $(i,j)$ の組について、チーム $i$ がチーム $j$ との試合に $f(g_{i,j} \rightarrow t_{i})$ 回勝つとする。このとき $i$ と $j$ の間の試合は $f(g_{i,j} \rightarrow t_{i}) + f(g_{i,j} \rightarrow t_{j})$ $= f(s \rightarrow g_{i,j}) = G[i,j]$ 回行われるので、全ての試合が終わっている。また $i$ が試合に勝つのは $\sum_{j} f(g_{i,j} \rightarrow t_{i}) = $ $f(t_{i} \rightarrow t) \leq $ $W[n] + R[n] - W[i]$ 回なので、シーズン累計の勝利数は $W[n] + R[n]$ 回以下である。したがってチーム $n$ が残りの試合全てに勝つならば $n$ は一位でシーズンを終えられる。 $\Box$

好きなチームが勝つかどうかを判定する方法をまとめると、まずフローネットワークを構築し、最大フローを計算し、その最大フローが $s$ から出る辺を全て飽和させるかどうかを見ればよいということになります。例えば上記のグラフでは $s$ から出る辺の容量の和は (Detroit が関わらない残り試合数と等しい) 27 ですが、$t$ へ向かう辺の容量の和は 26 しかありません。つまり最大フローの値は 26 以下にしかなれず、Detroit は数学的に敗退していると結論できます¹¹。

フローネットワークは $O(n^{2})$ 個の頂点と $O(n^{2})$ 個の辺を持ち、$O(n^{2})$ 時間で構築できます。よって Orlin のアルゴリズムを使えば最大フローを $O(VE) = \pmb{O(n^{4})}$ 時間で計算可能です。

このアルゴリズムはペナントレースの敗退問題に対する最速のアルゴリズムではありません。2001 年、Kevin Wayne (ケビン・ウェイン) は数学的に敗退する全てのチームをわずか $\pmb{O(n^{3})}$ 時間で見つけるアルゴリズムを発見しました。突き詰めればこのアルゴリズムも最大フローの計算を一度だけ使っています。

プロジェクト選択

最後の例として、与えられた $n$ 個のプロジェクトの中から実際に行うものを選択する問題を考えます。いくつかのプロジェクトは他のプロジェクトが終わるまで開始できず、その依存関係が有向非巡回グラフ $G$ で表されているとします。

$G$ の頂点はプロジェクトを表し、辺 $u \rightarrow v$ はプロジェクト $v$ が完了するまでプロジェクト $u$ に取り掛かれないことを表します (6.4 節で考えた依存グラフと同じ形式です)。そして各プロジェクトには完了したときに入手できる利益 $\$(v)$ が設定されており、負の利益を持つ (正のコストがかかる) プロジェクトも存在します。あなたが選ぶことができるのはプロジェクト集合の部分集合 $X$ であって、$X$ に含まれる任意のプロジェクトが依存するプロジェクトもまた $X$ に含まれるという条件を満たすものです。条件を満たすプロジェクトの部分集合であって利益の合計を最大化するものを見つけるのが目標です。例えば全てのプロジェクトに負の利益が設定されているなら、何も選ばないことを表す空集合が答になります。

図 11.6

8 個のプロジェクトからなる依存グラフ (ダイアモンド型の頂点が利益をもたらすプロジェクトを、四角の頂点がコストのかかるプロジェクトを表す。辺 $u \rightarrow v$ は $u$ が $v$ に依存することを示す)

抽象的に考えると、この問題の答えはプロジェクトの集合の二つの部分集合への分解、つまり選択するプロジェクトの集合 $S$ と選択しないプロジェクトの集合 $T$ への分解と捉えることができます。そのため、何らかのグラフにおける最小カットとしてこの問題をモデル化すれば良いのではないかという気がします。でもどんなグラフでしょう？依存関係を表現するにはどうすれば？ここで行いたいのは利益の最大化ですが、私たちが求められるのは最小カットだけです。どうすれば？負の利益を正の容量に変換するにはどうすればいいのでしょうか？

与えられた制約グラフ $G$ をフローネットワーク $G^{\prime}$ に変換するために、$G$ にソース頂点 $s$ とシンク頂点 $t$ を追加し、利益の出る ($\$ (v) > 0$ である) プロジェクト $v$ に対して辺 $s \rightarrow v$ を追加し、コストのかかる ($\$ (u) < 0$ である) プロジェクト $u$ に対して辺 $u \rightarrow t$ を追加します。$G^{\prime}$ の辺の容量は次のようにします:

利益の出るプロジェクト $v$ については $c(s \rightarrow v) = \$ (v)$
コストのかかるプロジェクト $u$ については $c(u \rightarrow t) = -\$ (u)$
その他の依存関係を表す辺 $u \rightarrow v$ について $c(u \rightarrow v) = \infty$

こうすれば辺の容量が正となるので、$G^{\prime}$ は最小カット問題の正しい入力となります。

$G^{\prime}$ における任意の $(s,t)$-カット $(s, t)$ を考えます。元の依存グラフ $G$ にあった辺 $u \rightarrow v$ に対して $u \in S$ かつ $v \in T$ なものが存在するなら $\|S, T\| = \infty$ です。したがって、カット $(s, t)$ の容量が有限のときに限って $S$ が実行可能なプロジェクトの集合としての条件を満たすということが言えます。

図 11.7

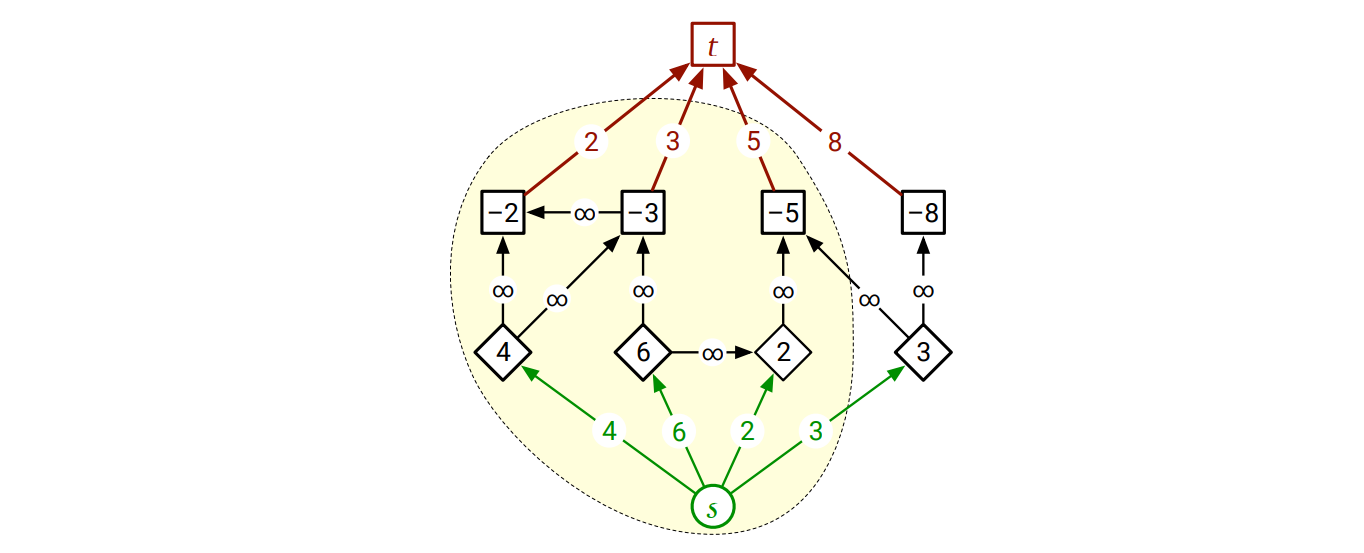
例の依存グラフに対するフローネットワークと容量 $13$ の最小カット。$P = 15$ なので、このカットによって選択されるプロジェクト全体の利益は $2$ である。

$G^{\prime}$ における小さい容量のカットが高い利益を持つプロジェクトの集合に対応することをこれから示します。具体的には、プロジェクトの集合として $S$ を選ぶと利益が $P - \|S,T\|$ となることを示します。ここで $P$ は正の利益の和です: \[ P = \sum_{v} \max \lbrace 0, \$ (v) \rbrace = \sum_{\$(v) > 0} \$(v) \] 証明は定義を追っていくだけで済みます。任意のプロジェクトの集合 $X$ について、次の三つの値を定義します: \[ \begin{aligned} \mathit{cost}(X) & := \sum_{u \in X, \$(u) < 0} - \$ (u) = \sum_{u \in X} c(u \rightarrow t) \\ \mathit{yeild}(X) & := \sum_{v \in X, \$(v) > 0} \$ (u) = \sum_{v \in X} c(s \rightarrow v) \\ \mathit{profit}(X) & := \sum_{v \in X} \$(v) = \mathit{yeild} (X) - \mathit{cost}(X) \end{aligned} \] (存在しない辺 $u \rightarrow v$ については $c(u \rightarrow v) = 0$ とします) 定義より $P = \mathit{yeild}(V) = \mathit{yeild}(S) + \mathit{yeild}(T)$ です。カット $(S, T)$ は有限の容量を持つので、$S$ と $T$ を結ぶ辺は $s \rightarrow v$ または $u \rightarrow t$ という形をしています。また $G^{\prime}$ の構成より辺 $s \rightarrow v$ について $v$ は利益をもたらすプロジェクトであり、辺 $u \rightarrow t$ について $t$ はコストのかかるプロジェクトです。よって $\|S, T\| = \mathit{cost}(S) + \mathit{yeild}(T)$ であり、直ちに $P - \|S,T\| =$ $\mathit{yeild} (S) - \mathit{cost}(S) =$ $\mathit{profit}(S)$ となって目当ての式が得られます。

よって $G^{\prime}$ の最小カットを求めることで全体の利益を最大化できます。$G$ からは $O(V+E)$ 時間で $G^{\prime}$ を構築でき、$G^{\prime}$ の最小 $(s,t)$-カットは Orlin のアルゴリズムを使えば $O(VE)$ 時間で計算できるので、プロジェクト選択のアルゴリズム全体の実行時間は $\pmb{O(VE)}$ です。

練習問題

$G = (V,E)$ を有向グラフとし、各頂点の入次数と出次数が等しいとします。$G$ が $u$ から $v$ への大きさ $k$ の辺素路集合を含むとき、$G$ は $v$ から $u$ への大きさ $k$ の辺素路集合を含みますか？証明または反例とその説明を示してください。
無向グラフ $G = (V,E)$ と三つの頂点 $u,v,w$ が与えられたとします。$u$ から $w$ への $v$ を通る路があるかどうかを判定するアルゴリズムを説明、解析してください。 [ヒント: $G$ が有向グラフだとこの問題は NP 困難です！]
有向グラフ $G = (V,E)$ と複数のソース頂点 $s_{1}, s_{2}, \ldots, s_{\sigma}$ と複数のシンク頂点 $t_{1}, t_{2}, \ldots, t_{\tau}$ が与えられたとします。ソースかつシンクである頂点は存在しません。多終端フロー (multi-terminal flow) とは、関数 $f: E \rightarrow \mathbb{R}_{\geq 0}$ であってソースでもシンクでもない全ての頂点において保存条件が満たされるものを言います。多終端フロー $f$ の値 $|f|$ とは全てのソース頂点から出るフローの和です: \[ |f| := \sum_{i=1}^{\sigma} \left(\sum_{w} f(s_{i} \rightarrow w) - \sum_{u} f(u \rightarrow s_{i}) \right) \] 通常のフローと同じように、求めたいのは辺の端点において制約が満たされるフローで最大のものです。フローがどのソース頂点から出るか、あるいはどのシンク頂点へ向かうかは考えません。
1. 多終端フローを計算する次のアルゴリズムを考えます。ここで変数 $f$ と $f^{\prime}$ はフロー関数を表し、サブルーチン $\textsc{MaxFlow}(G, s, t)$ はソース $s$ からシンク $t$ への通常の最大フローを求めます。
  
  procedure $\texttt{MaxMultiFlow}$($G, s[1..\sigma], t[1..\tau]$)
  
  ⟨⟨フローを初期化する⟩⟩
  
  $f \leftarrow 0$
  
  for $i \leftarrow 1$ to $\sigma$ do
  
  for $j \leftarrow 1$ to $\tau$ do
  
  $f^{\prime} \leftarrow$$\texttt{MaxFlow}$($G_{f}, s[i], t[j]$)
  
  ⟨⟨フローを更新する⟩⟩
  
  $f \leftarrow f + f^{\prime}$
  
  return $f$
  
  このアルゴリズムが $G$ の最大多終端フローを正しく計算することを証明してください。
2. $G$ の最大多終端フローを正しく計算するもっと効率の良いアルゴリズムを説明してください。
Sodor 島にはたくさんの街と村があり、大規模な鉄道網によって繋がっています。ついこのあいだ致死性の伝染病 (豚インフルエンザあるいはゾンビ: 報告ははっきりしません) が Skarloey 村で何件か確認されました。Sodor 鉄道の管理者であるあなたは、いくつかの駅を封鎖して列車が止まらないようにすることで彼の住む村 Tidmouth に病気が広がらないようにしたいと考えています。ただし費用 (と広報の手間) を最小限にするために、閉鎖する駅の数は最小限にしたいとします。また閉鎖の報告をするために伝染した駅に行くことは避けたいので、Skarloey 駅を閉鎖することはできません。それからお気に入りのパブがある Tidmouth 駅を閉鎖することもできません。

Skarloey 駅から Tidmouth 駅へ向かう鉄道路を全てブロックするために閉鎖しなければならない駅の数の最小値を求めるアルゴリズムを説明、解析してください。Sodor 鉄道のネットワークは無向グラフによって表され、頂点が駅を、辺がその間の線路を表します。Skarloey 駅と Tidmouth 駅を表す二つの特別な頂点 $s, t$ も入力に含まれます。

例えば次のグラフが入力された場合にはアルゴリズムは整数 $2$ を返します。
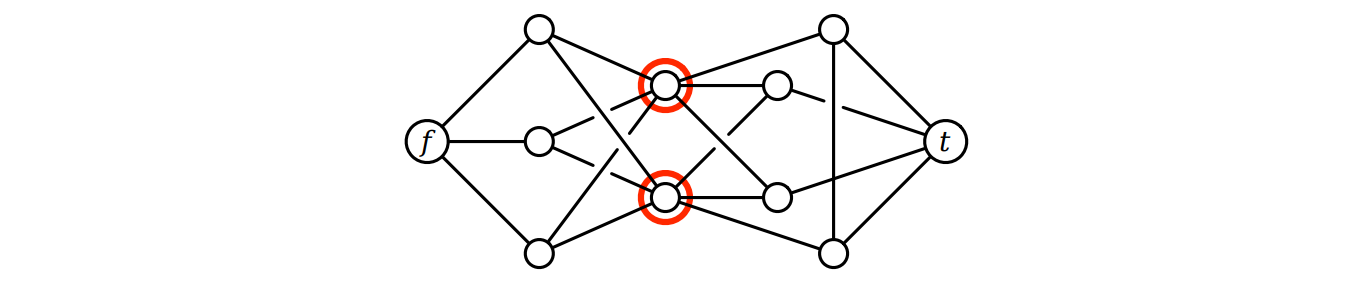
$n \times n$ の格子は $n^{2}$ 頂点の無向グラフとみなすことができます。$i$ 行 $j$ 列の頂点を $(i,j)$ と表記すると、$i = 1$, $i = n$, $j = 1$, $j = n$ を満たす境界上にある頂点を除いた各頂点 $(i,j)$ はちょうど四つの頂点 $(i-1, j),$ $(i+1, j),$ $(i, j-1),$ $(i,j+1)$ と隣接します。

$m$ 個の異なる頂点 $(x_{1}, y_{1}),$ $(x_{2}, y_{2}),$ $\ldots,$ $(x_{m}, y_{m})$ を終端 (terminals) とします。脱出問題 (escaping problem) とは、終端の頂点と境界上にある頂点を結ぶ $m$ 個の頂点素路が存在するかどうかを判定する問題です。

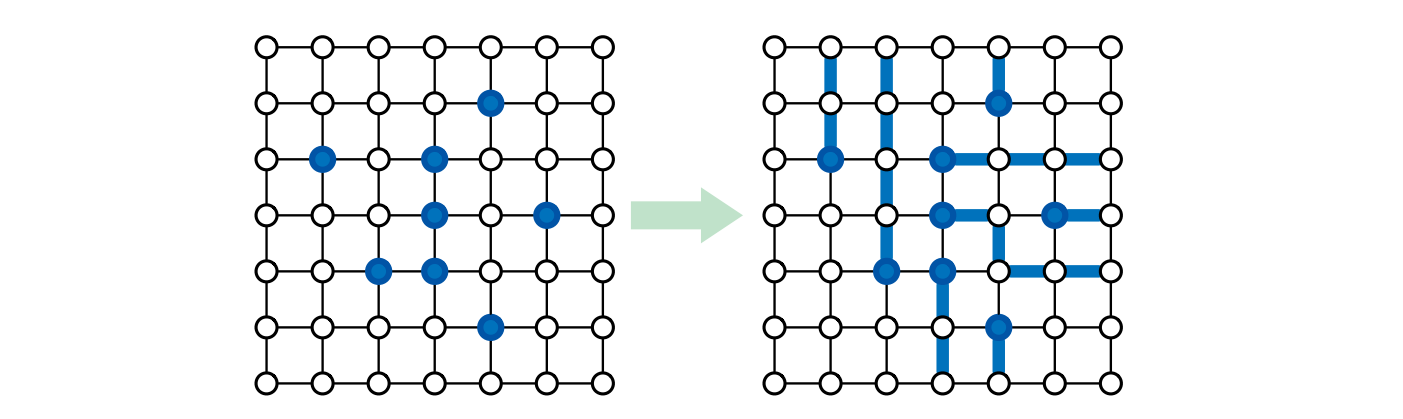図 11.8

解を持つ脱出問題のインスタンスとその解
1. 脱出問題を解く効率の良いアルゴリズムであって実行時間が次数の小さい $n$ の多項式で抑えられるものを説明、解析してください。
2. 脱出問題の入力が整数 $n$ と $m$ 個の終端頂点からなるとします。このとき $m$ を小さい値に固定すると、前問のアルゴリズムの実行時間は入力の長さに対して指数的になってしまいます！脱出問題を解くアルゴリズムで実行時間が $m$ の多項式時間であるものを説明してください。
3. ❤ 前問のアルゴリズムを変更して、脱出路が存在する場合にはその路を返すようにしてください。実行時間は $m$ の多項式のままとしてください。
SPU の情報科学科が See-Bull Center の地下にミニゴルフ場を作ることになりました！ゴルフのコースは $m$ 個の水平または垂直な線分からなる多角形であり、コースにはスタート地点とゴール地点の組が $n$ 個あります。スタートとゴールは壁にぶつからない直線で結ぶことができ、(高級なガラスでできた) 壁にボールを当てる必要はありません。また $n$ 個のスタート地点と $n$ 個のゴール地点は全て異なる点です。

残念なことに、工事に取り掛かろうとしたちょうどそのとき、コース設計者のコンピューターがクラッシュしてしまいました。システム管理者のすさまじい努力によってスタート地点とゴール地点の場所は復元できたのですが、どのスタートがどのゴールに対応しているかという情報は失われてしまいました！

スタート地点とゴール地点の直線で結ばれる対応関係を全て計算するか、そのような関係を作ることが不可能ならそうだと正しく報告するアルゴリズムを説明、解析してください。入力はコースの $m$ 個の角、$n$ 個のスタート地点、$n$ 個のゴール地点の $x, y$ 座標からなります。端点の $x,y$ 座標で表された二つの線分が交わるかどうかを定数時間で判定できるとしてください。

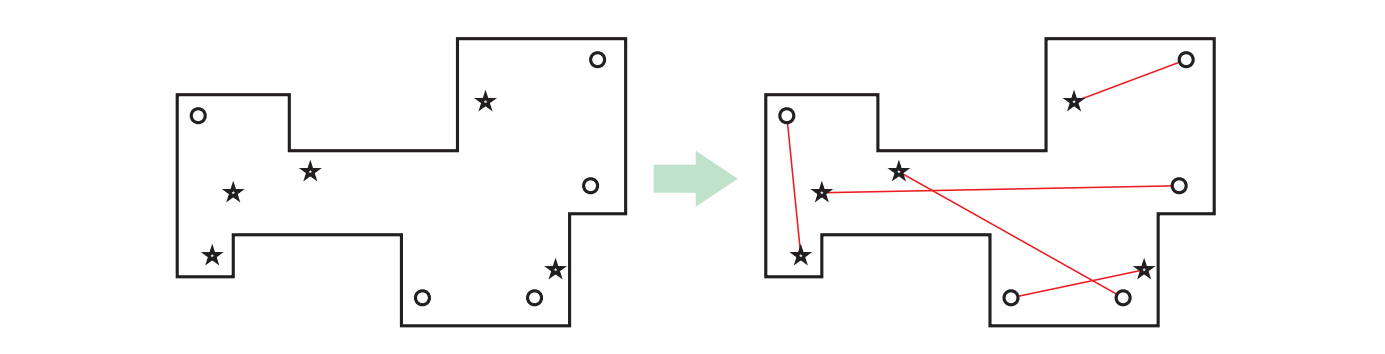$$5$ 個のスタート地点 (*) とゴール地点 (○) を持つミニゴルフコース、そして条件を満たすスタートとゴールの対応関係$

図 11.9

$5$ 個のスタート地点 (*) とゴール地点 (○) を持つミニゴルフコース、そして条件を満たすスタートとゴールの対応関係
有向グラフ $G = (V, E)$ の閉路被覆 (cycle cover) とは、$G$ に含まれる閉路の集合であって $G$ の各頂点がいずれかの閉路にちょうど一回ずつ含まれるものを言います。与えられた有向グラフの閉路被覆を見つけるか、閉路被覆が存在しないならそうだと正しく報告する効率の良いアルゴリズムを説明、解析してください。 [ヒント: 二部グラフのマッチングを使ってください！]
$n \times n$ のチェッカーボードからいくつかのマスを取り除いたものが与えられ、あなたは二マスのドミノをたくさん持っているとします。このドミノでボードを埋め尽くせるかどうかを判定するアルゴリズムを説明、解析してください。各ドミノはちょうど二マス分を埋め、全てのマスはちょうど一つのドミノによって埋められるとします。

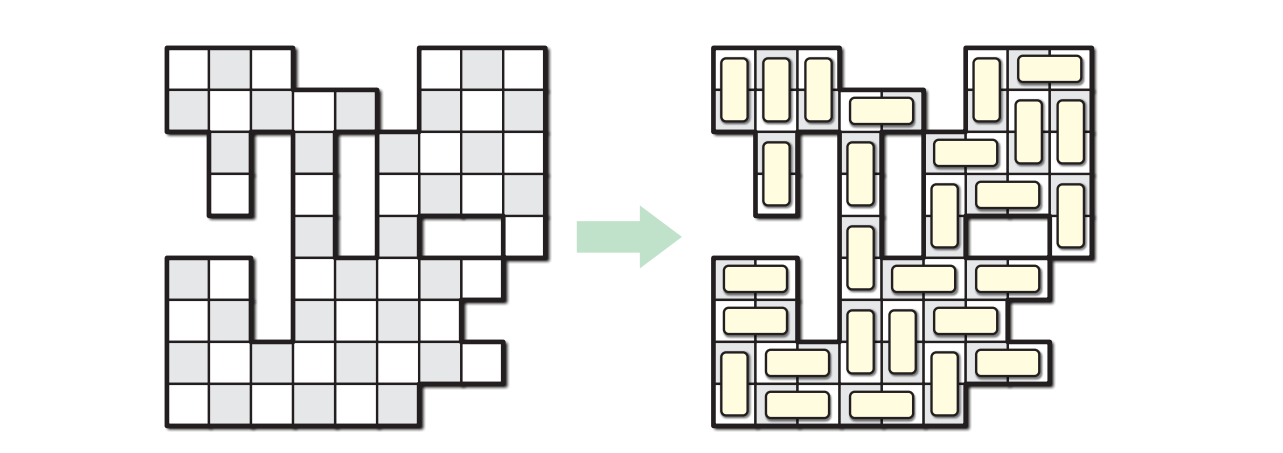図 11.10

穴の開いたチェッカーボードをドミノで埋める

入力は $\mathit{Deleted}[i..n,i..n]$ であり、$\mathit{Deleted}[i,j] = \textsc{True}$ は $i$ 行 $j$ 列目のマスが取り除かれていることを表します。出力は一つの真偽値であり、ドミノの実際の配置を計算する必要はありません。例えば上図のボードに対するアルゴリズムの答えは $\textsc{True}$ です。
マスが黒または白に塗られた $n \times n$ の格子が与えられたとします。次の条件を満たすように駒をマスに置けるかどうかを判定するアルゴリズムを説明、解析してください。
- 全ての駒は白いマスにある。
- 全ての行にはちょうど一つの駒がある。
- 全ての列にはちょうど一つの駒がある。
入力はどのマスが白いかを表す真偽値の二次元配列 $\mathit{IsWhite}[1..n, 1..n]$ であり、出力は真偽値一つです。例えば以下の格子が与えられたときのアルゴリズムの答えは $\textsc{True}$ です。

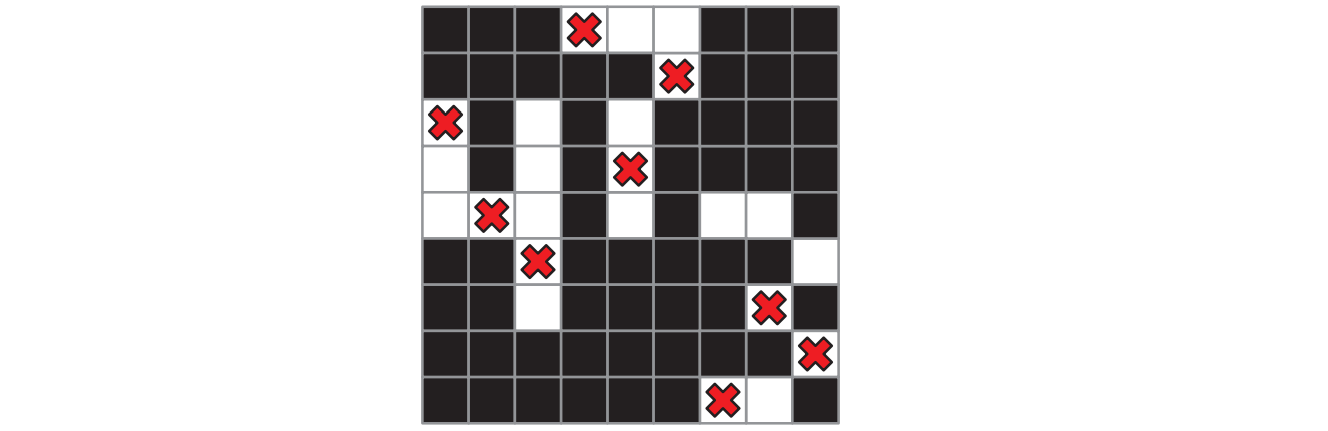図 11.11

全ての列と行に駒を置く
いくつかの箱が与えられるとします。それぞれの箱は幅、高さ、奥行きの値を持っており、全て 10 cm から 20 cm の間です。分かるとは思いますが、ある箱を回転させて幅、高さ、奥行きの全ての値を他の箱よりも小さくできる場合、小さい箱を大きい箱の中に収めることができます。ある箱が他のどの箱にも入っていないとき、その箱は見えている (visible) と言うことにします。

見えている箱の数が最小になるように箱を入れ子にするアルゴリズムを説明、解析してください。
$n \times n$ の格子が与えられ、いくつかのマスに印が付いているとします。つまり真偽値の配列 $M[1..n, 1..n]$ によって格子が表され、$(i, j)$ というマスに印が付いているときに限って $M[i,j] = \textsc{True}$ ということです。単調路 (monotone path) とは、格子の左上のマスから右下のマスへの路であって各ステップにおいて左または下にしか移動しないものを言います。この問題の目標は、印の付いた全てのマスをなるべく少ない単調路で被覆することです。

図 11.12

印の付いたマスを貪欲に単調路で被覆する
1. 被覆する印付きマスの数が最大となる単調路を計算するアルゴリズムを説明してください。
2. 簡単に思いつく貪欲なヒューリスティックとして、残っているセルを一番多く被覆する単調路を選択し、その路が被覆するマスの印を消し、再帰する、というアルゴリズムがあります。このアルゴリズムが常に最適解を計算するわけではないことを示してください。
3. 印の付いた全てのマスを被覆する単調路の集合の中で最小のものを計算する効率の良いアルゴリズムを説明、解析してください。
Sham-PooBanana 大学陸上チームの ~~マスコット~~ シンボル Factotum 男爵が不祥事を起こしたことを受けて、学部評議委員会は Gabby おじさんこと Bobo Cornelius とサイキックゴリラこと Mofo のどちらを代役にするかを選ぶ決議を行うことになりました。委員会には各学部から一人が代表として出席します。複数の学部に所属している委員もいますが、その委員が代表できるのは一つの学部だけです。例えば Blagojevich 教授が破壊学科 (Department of Corruption) と愚鈍学科 (Department of Stupidity) の委員である場合、Blagojevich 教授が愚鈍の代表として選ばれたときには破壊の代表は別の人である必要があります。また学部評議委員会に出席する助教授、准教授、教授の数は等しくなければならないと大学の規則で定められています。幸運にも学科の数は $3$ の倍数です。

ポスト Factotum Simian ~~マスコット~~ シンボル委員会を開くことができる SPU スタッフの部分集合を計算するか、どうやっても委員会を開くことはできないと正しく報告するアルゴリズムを説明、解析してください。アルゴリズムの入力はどの教授がどの学科に所属しているかを表す二部グラフであり、教授を表す頂点は教授のランク (助教授、准教授、教授) でラベル付けされています。
Sham-PooBanana 大学のコンピューターサイレンス学科 (Department of Commuter Silence) はフレキシブルなカリキュラムを持っており、卒業のための条件が複雑です。学科は $n$ 個の異なる講義を開講していて、卒業のための条件が $m$ 個あります。それぞれの条件は講義の部分集合とその中から取らなければいけない講義の数を指定します。異なる条件が指定する講義は重複することがありますが、一つの講義を条件を満たすために使ってよいのは一度だけです。

例えば $n = 5$ で $A, B, C, D, E$ という講義があり、$m = 2$ で次の条件があるとします:
- $\lbrace A,B,C \rbrace$ の中から少なくとも二つの講義を取らなければならない。
- $\lbrace C,D,E \rbrace$ の中から少なくとも二つの講義を取らなければならない。
このとき $B, C, D$ という講義を取った生徒は卒業できず、$A,B,C,D$ および $B,C,D,E$ という講義を取った生徒は卒業できます。

与えられた講義を取った生徒が卒業できるかどうかを判定するアルゴリズムを説明、解析してください。アルゴリズムの入力は $m$ 個の条件 (それぞれが講義の部分集合とその中から取るべき講義の数を指定する) と生徒の取った講義のリストです。
SPU コンピューターサイレンス学科主催第一回定期 72 時間ダンスエクスチェンジというイベントをあなたは主催しています。このイベントは金曜日、土曜日、日曜日にかけて行われ、DJ が順番に音楽のセットをかけていきます。大勢の DJ からの出演依頼が来たので、あなたの次の仕事は次の条件が満たされるように DJ を選ぶことです:
- 一日にちょうど $k$ セット、三日間で合計 $3k$ セットの音楽を流す。
- ある DJ が一度の出演で流すセットには同じジャンルの曲だけが含まれる (アンビエント、バブルガム、ダブステップ、ホラーコア、K-ポップ、クワイト、マリアッチ、ストレートアヘッドジャズ、トリップ・ホップ、ナッシュビル、カントリー、パラパラ、スカ...)。
- 同じジャンルのセットを流せるのは一日に最大でも一度だけ。
- 候補となっている DJ が流したい曲のジャンルのリストをあなたは持っている。
- イベント全体で同じ DJ が出演できるのは三回まで。
候補となっている DJ が $n$ 人いて、曲のジャンルが $g$ 個存在するとします。DJ とジャンルを $3k$ 個のセットに対応させるか、そのような対応は存在しないと正しく報告するような効率の良いアルゴリズムを説明、解析してください。
あなたはウェブサイトを管理していて、毎日決まった人がサイトを訪問しているとします。サイトの訪問者は一つ以上の人口統計学的グループに所属していて、例えばある人物は 40-50 才で、子持ちの男性で、イリノイ在住で、大学で働いていて、ブロガーで、Gilbert and Sullivan のファンである¹²などの情報が分かるとします。あなたのサイトは広告によって支えられており、広告主はどの人口統計学的グループに広告を見せるべきか、および広告を一日に何回見せなければならないかを指定しています。全部で $n$ 人の訪問者と $k$ 個の人口統計学的グループと $m$ 個の広告主がいます。

以上の情報が全て与えられたとき、全ての訪問者に一日にちょうど一つだけの広告を見せることで、全ての広告主の広告を指定した回数だけ指定したグループに見せることができるかどうかを判定する効率の良いアルゴリズムを説明、解析してください。
非負実数の配列 $A[1..m][1..n]$ が与えられたとします。$A$ の各要素 $x$ を $\lceil x \rceil$ または $\lfloor x \rfloor$ に入れ替えることで、各行および各列の要素の和を変更せずに $A$ を整数行列に丸めたいとします。例えば \[ \begin{bmatrix} 1.2 & 3.4 & 2.4 \\ 3.9 & 4.0 & 2.1 \\ 7.9 & 1.6 & 0.5 \end{bmatrix} \mapsto \begin{bmatrix} 1 & 4 & 2 \\ 4 & 4 & 2 \\ 8 & 1 & 1 \end{bmatrix} \] はこの条件を満たす丸めです。
1. 条件を満たすように $A$ を丸めるか、そのような丸めは存在しないと正しく報告する効率の良いアルゴリズムを説明、解析してください。
2. 条件を満たす丸めが存在するのは各列および各行の要素の和が全て整数である場合に限ることを示してください。言い換えると、(a) のアルゴリズムが条件を満たす丸めを返さないときには、丸めが不可能なことが「明らか」であることを示してください。
3. ❤ $A$ の要素に整数が含まれないとします。条件を満たすように $A$ を丸めるか、そのような丸めは存在しないと正しく報告するさらに効率の良いアルゴリズムを説明、解析してください。満点のためにはアルゴリズムの実行時間が $O(mn)$ であることが求められます。 [ヒント: フローを使わないでください。]
アドホックネットワーク (ad-hoc network) は低消費電力のデバイスからなるネットワークであり、理論上は¹³自然災害で被害を受けた地域や戦場といった人が近づけない領域におけるネットワークとして機能します。アドホックネットワークのアイデアは、対象の領域に安価で単純なデバイスを (航空機から落とすなどして) 大量に撒いて、その後デバイス自身に無線ネットワークを自動的に構築させるというものです。

デバイスが通信できる距離は限られています。ここでは全てのデバイスは同一であり、任意の二つのデバイスが通信できるのはデバイス間の距離が $D$ 以下のときだけだと仮定します。

もちろんアドホックネットワークの信頼性は高いことが望ましいのですが、デバイスは安価で利用できる電力も小さいので、よく故障します。デバイスが故障の前兆を検出した場合、そのデバイスは自身の情報を通信可能な範囲にあるバックアップデバイスに送信します。各デバイス $x$ は距離 $D$ 以内にバックアップデバイスを $k$ 個持たなくてはいけないとします (この $k$ 個のデバイスを $x$ のバックアップ集合と呼ぶことにします)。またあるデバイスにネットワークが集中するのも避けたいので、一つのデバイスがあまりに多くのデバイスのバックアップ集合に含まれることもあってはいけません。

通信半径 $D$ とパラメータ $b,k$ と配列 $d[1..n,1..n]$ が与えられ、$d[i,j]$ がデバイス $i$ と $j$ の間の距離を表すとします。$n$ 個の頂点それぞれに対する大きさ $k$ のバックアップ集合であって、どの頂点も他の頂点のバックアップ集合に $b$ 回以下しか現れないものを計算するか、そのような集合は作れないと正しく報告するアルゴリズムを説明してください。
予算削減の危機にさらされた Potemkin 大学の理事は、講義が満員であるように見せかけるために、役者を雇って "生徒" として講義に出席してもらうことにしました。役者を雇うのは高くつくので、雇う役者の数は最小限にしたいと考えています。

Potemkin 大学の理事は今は亡き Sham-PooBanana 大学で培ったリーダーシップを発揮して、あなたを問題解決者として任命しました。あなたには有向非巡回グラフ $G=(V,E)$ が与えられ、頂点が講義を、辺 $i \rightarrow j$ が "生徒" が講義 $i$ に出席した後に講義 $j$ に出席できることを表します。加えて配列 $\mathit{cap}[1..V]$ も与えられ、$\mathit{cap}[i]$ が講義 $i$ に出席できる "生徒" の数の最大値を表します。全ての講義を満員にするために必要になる "生徒" の数を計算するアルゴリズムを説明、解析してください。
Quentin と Alice と Brakebills Physical Kid たちは NeitherLands を経由して Fillory まで行く旅を計画しています。NeitherLands は放棄された広大な都市であり、異世界へと通じる魔法の噴水が置かれたいくつかの広場から構成されています。隣接する広場は門でつながっており、門は Beast によって呪われています。広場の間の門は全て同じ時間に開閉し、開くのは 12:00 から 12:05 まで、1:00 から 1:05 までという風に一時間ごとに五分間だけです。この五分間の間に一つの門につき一人だけが通り抜けることができ、二人以上が門を通り抜けると Beast に気付かれてしまいます¹⁴。また閉じている門を開けようとしたり、五分間の間に二つ以上の門を通り抜けようとした人間は niffin に変えられてしまいます¹⁵。ただし異なる人間が異なる門を同時に通り抜けること、あるいは同じゲートを異なる時間帯に通り抜けることは可能です。

あなたは NeitherLands の地図を持っています。地図は頂点が噴水、辺が門を表す無向グラフ $G$ であり、地球と Fillory につながる噴水に印が付いています。
1. $G$ の他に正の整数 $h$ が与えられたとします。Beast に気付かれることも niffin に変えられることもなく $h$ 時間以内に ――つまり、門が $h$ 回開くまでに―― 地球から Fillory に移動できる人数の最大値を計算するアルゴリズムを説明、解析してください。実行時間は $h$ に依存するはずです。 [ヒント: 二部グラフを作ってください。]
2. ♣ ❤ (a) に対するアルゴリズムであって実行時間が $V$ と $E$ の多項式であり $h$ に依存しないものを説明、解析してください。
3. 追加のパラメータとして $h$ ではなく正の整数 $k$ が与えられたとします。Beast に気付かれることも niffin に変えられることもなく $k$ 人の人間が地球から Fillory に移動するときにかかる時間の最小値を求めるアルゴリズムを説明、解析してください。 [ヒント: (a) を使ってください。]
❤ $G = (L \sqcup R, E)$ を二部グラフとし、左側の頂点を $L = \lbrace l_{1}, l_{2}, \ldots, l_{n} \rbrace$、右側の頂点を $R = \lbrace r_{1}, r_{2}, \ldots, r_{n} \rbrace$ とします。$G$ のマッチング $M$ が非交差 (non-crossing) であるとは、任意の辺の組 $l_{i}r_{j}$ と $l_{i^{\prime}} r_{j^{\prime}}$ において $i < i^{\prime} \iff j < j^{\prime}$ なことを言います。
1. $G$ の最大非交差マッチングを見つけるアルゴリズムを説明、解析してください。 [ヒント: 実はこの問題ではフローを使いません。]
2. 非交差マッチングの集合 $\lbrace M_{1}, M_{2}, \ldots, M_{k} \rbrace$ であって $G$ の任意の辺がちょうど一つのマッチング $M_{i}$ に含まれるものの大きさの最小値を求めるアルゴリズムを説明、解析してください。 [ヒント: この問題ではフローを使います。]
❤ $G = (L \sqcup R, E)$ を二部グラフとし、左側の頂点が適当な順序で $L = \lbrace l_{1}, l_{2}, \ldots, l_{n} \rbrace$ と添え字が付いているとします。
1. $G$ のマッチング $M$ が密 (dense) であるとは、$L$ の任意の連続する頂点の少なくとも一方がマッチされていることを言います。つまり、任意の添え字 $i$ について $l_{i}$ または $l_{i+1}$ のどちらかが $M$ の辺に隣接するということです。$G$ に密なマッチングが存在するかを判定するアルゴリズムを説明してください。
2. $G$ のマッチング $M$ が疎 (sparse) であるとは、$L$ の任意の連続する頂点の少なくとも一方がマッチされていないことを言います。つまり、任意の添え字 $i$ について $l_{i}$ または $l_{i+1}$ のどちらかが $M$ の辺に隣接していないということです (例えば空のマッチングは疎です)。$G$ の疎なマッチングで最大のものを見つけるアルゴリズムを説明してください。
3. $G$ のマッチング $M$ が回文 (palindromic) であるとは、任意の添え字 $i$ について $l_{i}$ と $l_{n-i+1}$ が両方 $M$ の辺に隣接するか、そうでなければどちらも $M$ の辺に隣接しないことを言います (例えば空のマッチングは回文です)。$G$ の回文であるマッチングで最大のものを見つけるアルゴリズムを説明してください。
いずれの問題においても $R$ の頂点に関するマッチの制限はありません。
❤ 根付き木 (rooted tree) とは、有向非巡回グラフであって根と呼ばれる頂点を除いた全ての頂点 $v$ について $v$ に向かう辺が一つしか存在せず、さらに根に向かう辺が無いものを言います。同じことですが、根付き木は根の頂点と根から延びるゼロ個以上の小さな根付き木への辺からなると言うこともできます。二つの根付き木 $A, B$ が与えられたときに、ある $A$ の部分グラフと同型であり、かつある $B$ の部分グラフとも同型である根付き木のうち最大のものを計算する効率の良いアルゴリズムを説明してください。つまり、二つの根付き木の最大共通部分木を求めるアルゴリズムを説明してください。

[ヒント: 全ての頂点が $O(1)$ 個の子しか持たないとき、あるいは各頂点の子が一列に順序付けられるときにはこの問題は比較的簡単な動的計画法の問題となります。しかし次数の大きい順序の付いていない木に対しては、再帰的な小問題を効率良く組み合わせる別のテクニックが必要になります。]

この問題は四章で扱った安定マッチング問題とは大きく異なります。ここでは個々の医師と病院をなるべく幸せにするということを考えません。^[return]
この問題に対する標準的な名前を見つけられなかったので、タプル選択という言葉は自分で作りました。この問題が「割り当て問題 (assignment problem)」と呼ばれることもありますが、この言葉が指すのは辺に重みの付いた二部グラフに対する最大重み二部マッチングを求める問題であることが多いです。^[return]
隣り合わない集合の組 ($j > i + 1$ に対する $X_{i}$ と $X_{j}$) に関する制約が一つでもあった場合、この問題は $\textsc{Exact3Dimenstional}$$\textsc{Matching}$ からの簡単な帰着によって NP 困難となります。NP 困難性については次の章で扱います。^[return]
アメリカなら proctor、アメリカ以外なら invigilator と呼ばれます。^[return]
この情報を最初からグラフで表した方が良いのは間違いないのですが、そうすると帰着が分かりにくくなると私は考えました。^[return]
この問題のもう少し現実的な (気分が落ち込むこともない) 例としては、教授と講義の部分を飛行機とフライト、あるいはバスと運行ルートなどに変えたものを考えてください。^[return]
ただし生徒からのメールには教室を移動している間に返信できるとします。^[return]
全ての $u, v$ について $T[u,v]$ が同じだとした場合、スケジューリング問題は貪欲アルゴリズムを使って $O(n \log n)$ 時間で解けます (多くのアメリカの大学では講義の間の休み時間が 10 分であり、これは普通の人間がキャンパス内の任意の教室からキャンパス内の任意の教室へと 10 分以内に移動できるという興味深い仮定に基づいています。この仮定が現実的だと思うなら、私の大学のキャンパスに来て二つの Siebel Center の間を歩いてみることをお勧めします)。^[return]
この例とその説明は、Eli V. Olinick のウェブサイト https://s2.smu.edu/~olinick/riot/detroit.html からです。このページは Olinick が Ilan Adler, Alan Erera, Dorit Hochbaum と共に行った共同研究に基づいています。^[return]
試合が引き分けになることはなく、試合が中止になることもないとします。メジャーリーグではプレーオフ進出がかかった試合およびその他のほとんどの試合で引き分けはありませんが、レギュラーシーズンでは (戦争、自然災害、ハチの群れなどが原因で) 試合が中止になることがあります。^[return]
この例ではラッキーでした。$t$ へ向かう辺の容量の和が $s$ から出る辺の容量の和よりも大きいにもかかわらずチーム $n$ が敗退しているという状況はあり得ます。^[return]
I am a very good theoretical computer scientist, specifically, a geometric algorithm specialist.^[return]
実際はそうでもありませんが。^[return]
これはとても悪いです。^[return]
これはとてもとても悪いです。^[return]