再帰木

先ほどから何度も出てきている再帰木 (recursion tree) を説明しましょう。再帰木とは分割統治法で出てくる再帰方程式を解くためのツールであり、単純で、多くの問題に適用でき、視覚的に理解が簡単です。

再帰木では根につながっている頂点が再帰的な小問題を表します。頂点の値 (value) とは、その頂点が表す小問題を解くのにかかる時間から再帰呼び出しの分の時間を除いたものです。この定義から、アルゴリズムの実行時間は木に含まれる全ての頂点の値の和であることが分かります。

この考えをもっと理解するために、再帰呼び出し以外の処理に \(O(f(n))\) だけ時間がかかるような分割統治法のアルゴリズムを考えます。\(r\) 回の再帰呼び出しが行われ、再帰呼び出しのたびに問題のサイズが \(\frac{n}{c}\) になると仮定します。このとき \(O()\) 記法によって隠れる定数倍を無視すれば、アルゴリズムの実行時間 \(T(n)\) は次の再帰方程式に支配されます: \[ T(n) = rT(n/c) + f(n) \]

\(T(n)\) に対する再帰木の根の値は \(f(n)\) であり、根は \(r\) 個の子を持ちます。根の子は全てが \(T(n/c)\) に対する再帰木です。全ての頂点は根と同様に \(r\) 個の子を持ち、深さ \(d\) の頂点は値 \(f(n/c^{d})\) を持ちます (\(n/c^{d}\) を整数にするために \(n\) が \(c\) を何乗かしたものと仮定しても構いませんが、こう仮定しなくても結果は変わりません)。

実際に問題を解くときには、最初の二つか三つの木を書いた次のような図を描くとよいでしょう:

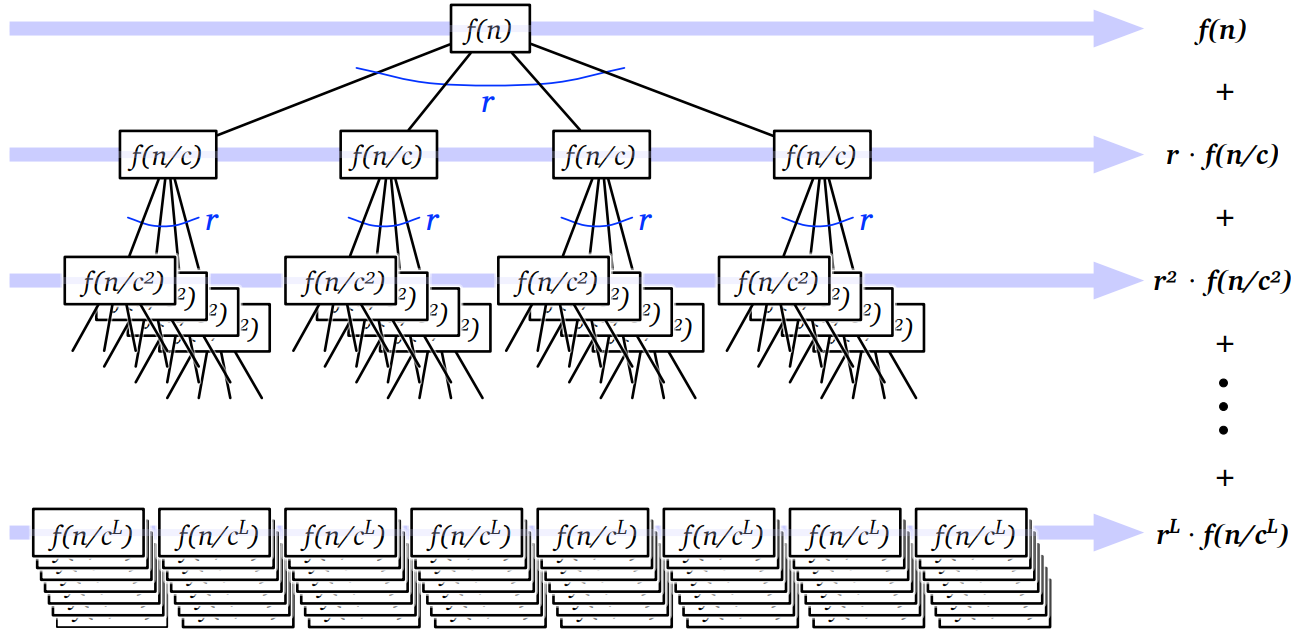
再帰方程式 \(T(n) = rT(n/c) + f(n)\) に対する再帰木
図 1.9
再帰方程式 \(T(n) = rT(n/c) + f(n)\) に対する再帰木

再帰木の葉は再帰方程式のベースケースに対応します。今は漸近表記にだけ注目しておりベースケースの正確な値は重要ではないので、全ての \(n \leq n_{0}\) について \(T(n) = 1\) と仮定しても問題ありません。ここで \(n_{0}\) は適当な正の整数定数であり、再帰木を解析するのに便利な値にするのがよいでしょう。ここでは \(n_{0} = 1\) としました。

\(T(n)\) は木に含まれる全ての値の和です。高さごとに和を求めることでこの和を計算します。整数 \(i\) に対して、高さ \(i\) の頂点はちょうど \(r^{i}\) 個存在し、全て \(f(n/c^{i})\) の値を持ちます。したがって \[ T(n) = \sum_{i=0}^{L} r^{i}f(n/c^{i}) \] となります。ここで \(L\) は木の高さです。ベースケースにおいて \(n_{0} = 1\) だったので、\(n/c^{L} = n_{0} = 1\) より \(\pmb{L = \log_{c} n}\) となります。木の葉は \(r^{L} = r^{\log_{c} n} = n^{\log_{c} r}\) 個だけあるので、これと \(f(1) = O(1)\) から、高さによる和 (\(\sum\)) の最後の項は \(n^{\log_{c} r} \cdot f(1) = O(n^{\log_{c}r})\) となります。

高さごとの級数 \(\sum\) が特に簡単に計算できる場合が三つあります:

一番目と三番目のケースでは、幾何級数の一番大きい項だけが生き残り、他の項は \(O(\cdot)\) 表記の中に飲み込まれてしまいます。減少する幾何級数のケースでは、 \(L\) を計算する必要さえありません。なお漸近上界は再帰が無限だったとしても正しくなります！

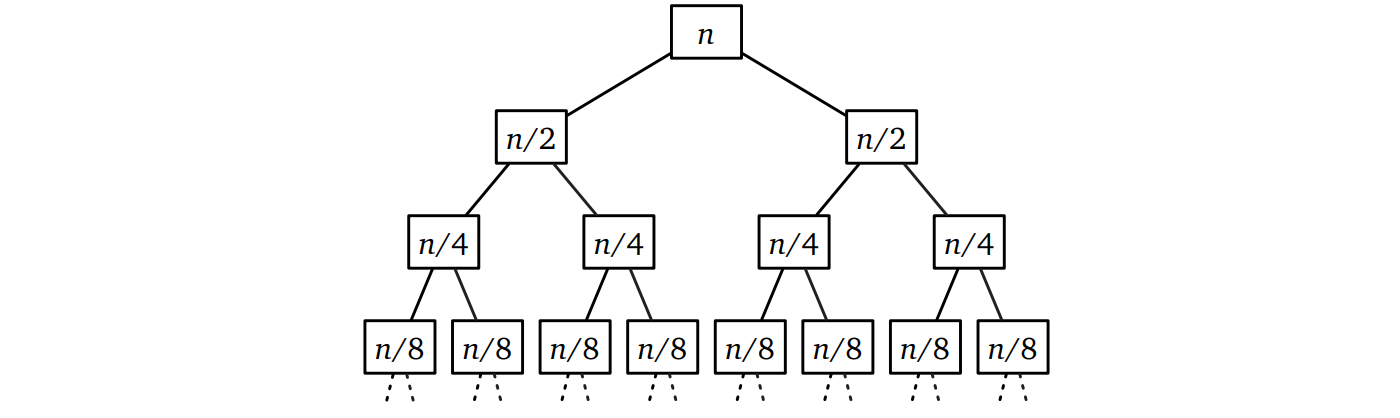
例えばマージソートの (簡略化された) 再帰方程式 \(T(n) = 2T(n/2) + O(n)\) について再帰木を書くと、最初のいくつかを書いた時点で同じ高さの頂点の値の和が全て等しいことが分かります (下図)。したがって \(T(n) = O(n \log n)\) がすぐに分かります。

マージソートに対する再帰木
図 1.10
マージソートに対する再帰木

再帰木のテクニックは小問題が異なる大きさを持つアルゴリズムにも適用できます。例えばクイックソートにおいて、何らかの方法でソートされた配列を三分割したときの中央の部分からピボットを必ずに選択できたとします。このとき最悪計算時間が満たす再帰方程式は \[ T(n) \leq T(n/3) + T(2n/3) + O(n) \] を満たします。この式は恐ろしく見えるかもしれませんが、手懐けるのは簡単です。再帰木を何段か書いてみれば、高さごとの値の和が最大でも \(n\) である ――木の深い部分ではノードの一部が無くなるので―― ことが分かります。さらに木の高さは \(\log_{3/2} n = O(\log n)\) なので、すぐに \(T(n) = O(n \log n)\) が分かります (さらに言えば、再帰木に含まれる葉の総数は \(\log_{3} n = \Omega (\log n)\) なので、この解析を改善できたとしても定数の範囲でしか改善できません。ただこの改善は私たちの目的には全く関係のないことです)。つまり、再帰木のバランスが取れていなくても関係ありません。

もっと極端な例として、最悪の場合のクイックソートに対する再帰方程式 \(T(n) =\) \(T(n - 1) + T(1) + O(n)\) を考えると、全くアンバランスな再帰木となります。高さごとの値の和は上述の三つの例のどれにも当てはまりませんが、どの項も \(n\) よりも小さく、木の高さが最大 \(n\) であることから、\(T(n) = O(n^{2})\) が分かります (少なくとも \(n/2\) 個の葉が \(n/2\) 以上の値を持っているので、ここでもこの保守的な解析が厳密であることが分かります)。

クイックソートの再帰木: ピボットが良い場合 (左) と最悪の場合 (右)
図 1.11
クイックソートの再帰木: ピボットが良い場合 (左) と最悪の場合 (右)

❤ 床関数と天井関数は無視してよい

注意深い読者はここまでのアルゴリズムの解析が重要な部分を無視していると思うかもしれません。というのもマージソートの実行時間は再帰方程式 \(T(n) = 2T(n/2) + O(n)\) に厳密には従わないのです。実際のプログラムでは入力サイズは奇数になるので、このように \(T(n)\) を表した場合、長さが \(42 \frac{1}{2}\) あるいは \(17 \frac{7}{8}\) の配列をソートするというような全く無意味な操作に対する時間を求めることになります。マージソートに対する本当の再帰方程式はもっと面倒くさいものでした: \[ T(n) = T(\lceil n/2 \rceil) + T(\lfloor n/2 \rfloor) + O(n) \]

もちろん帰納法を使えばこの再帰方程式でも \(T(n) = O(n \log n)\) であることは確かめられますが、うんざりするような計算が必要になります。しかし嬉しいことに、次に示す定義域変換 (domain transformation)という単純なテクニックを使うと、床関数と天井関数を再帰方程式から消すことができます1。

同様の定義域変換は床関数、天井関数、そして次数の小さい項を任意の分割統治法の再帰方程式から消すのに使えます。今こうして説明したので、これ以降は詳細を省略しましょう！ これから分割統治法の再帰方程式では、床関数と天井関数、そして次数の小さい項をそうと示さずに消すことにします。あなたにもそうすることを勧めます。

  1. 数学的に正しく言うと、ここでは \(T\) を整数についての関数ではなく実数に対する関数として扱うことでそれ以降の操作を可能にしています。この実数関数に対してある実数 \(C \geq 0\) および \(n_{0} \geq 0\) があって、全ての \(n \leq n_{0}\) で \(T(n) = C\) となりますが、この実数の値は重要ではありません。また \(n\) が整数のとき \(T(n)\) はサイズが \(n\) のときのアルゴリズムの実行時間を表しますが、これも議論に関係のないことです。[return]

広告
このページの文章はテキストゆれないくんを使って校正されました。