強連結性

有向グラフにおける連結性の正式な定義に戻りましょう。有向グラフ \(G\) の頂点 \(u\) が他の頂点 \(v\) に到達するとは、\(G\) に \(u\) から \(v\) への有向路があることを言い、\(\mathit{reach}(u)\) で \(u\) から到達できる頂点全体の集合を表しました。二つの頂点 \(u, v\) が強連結 (strongly connected) であるとは、\(u\) が \(v\) に到達し、かつ \(v\) が \(u\) に到達することを言います。有向グラフが強連結であるとは全ての頂点の組が強連結であることと同値です。

定義をうんざりするほどこねくり回すと、任意の有向グラフにおける強連結性が (無向グラフに対する接続性と同じように) 頂点集合に対する同値関係であることが示せます。この同値関係の同値類を、\(G\) の強連結成分 (strongly connected component) あるいはもっと単純に強線分 (strong component) と呼びます。同じことを言い換えると、\(G\) の強連結成分は \(G\) の極大な強連結部分グラフです。有向グラフ \(G\) が強連結であることは、\(G\) がちょうど一つの強連結成分を持つことと同値です。もう一方の極を考えると、有向グラフ \(G\) が DAG であることは \(G\) の全ての強連結成分が一つの頂点からなることと同値です。

強連結成分グラフ (strong component graph) \(\mathit{scc}(G)\) とは \(G\) の強連結成分を一つの頂点にまとめ、強連結成分の間の辺を一つに束ねることで得られる有向グラフのことです (強連結成分グラフはメタグラフ (meta-graph) あるいは凝縮グラフ (condensation graph) とも呼ばれます)。\(\mathit{scc}(G)\) が必ず DAG であることを示すのは難しくない (ヒント、ヒント) ので、少なくとも理論上は \(G\) の強連結成分をトポロジカル順序に並べられます。つまり、全ての頂点を一列に並べて全ての後方辺が同じ強連結成分にある頂点を結ぶようにできるということです。

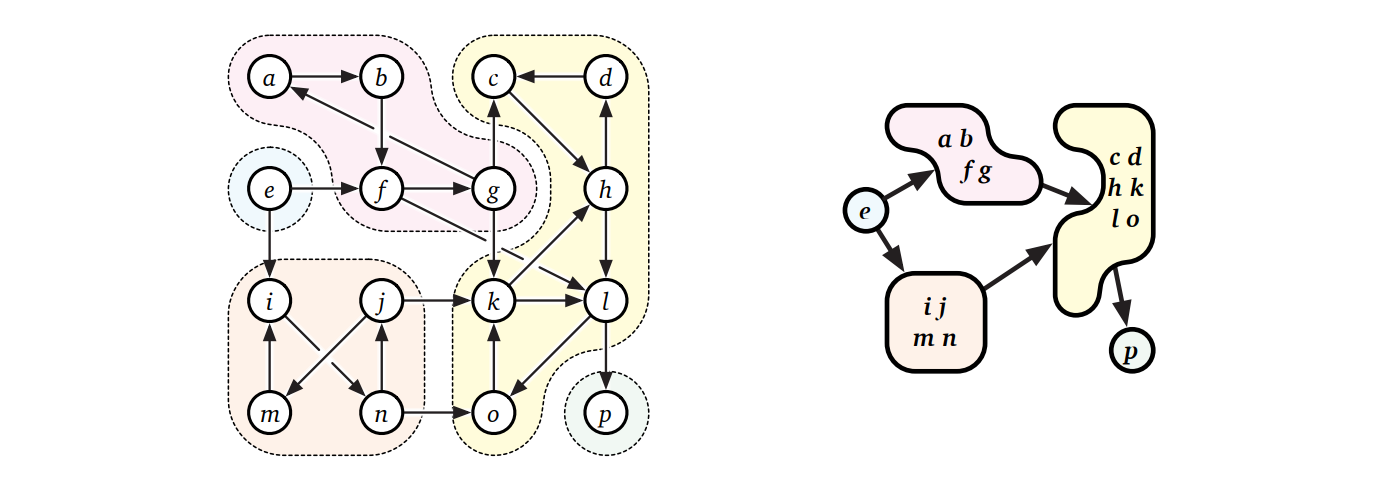
一つの頂点が属する強連結成分を \(O(V+E)\) で計算するのは簡単です。まず何か優先探索で \(\mathit{reach}(v)\) を計算し、次に \(G\) の逆を探索することで \(\mathit{reach}^{-1}(v) =\) \(\lbrace u\ |\ v \in \mathit{reach}(u) \rbrace\) を計算します。こうすれば、 \(v\) の強連結成分は二つの集合の交差 \(\mathit{reach}(v) \cap \mathit{reach}^{-1}(v)\) となります。このアルゴリズムを使えば、グラフ全体が強連結かどうかを \(O(V + E)\) 時間で判定できます。

同様に、このアルゴリズムを標準的なラッパー関数で包めば有向グラフの全ての強連結成分の計算できます。ただし、こうして出来上がるアルゴリズムの実行時間はグラフが DAG であったとしても \(O(VE)\) です: 強連結成分は最大で \(V\) 個あり、一つを計算するのに \(O(E)\) 時間かかるからです。もちろんこれは改善できます！ 前述の通り、全ての強連結成分が一つの頂点からなるかどうかは (深さ優先探索を使って) \(O(V + E)\) 時間で判定できるのですから。