カット
\(\pmb{(s, t)}\)-カット (ソースとシンクが明らかな場合は単にカット) とは、頂点集合の互いに素な二つの部分集合 \(S, T\) への分解であって \(s \in S\) かつ \(t \in T\) を満たすものを言います。\(S\) と \(T\) が互いに素とは \(S \cup T = V\) かつ \(S \cap V = \varnothing\) ということです。
容量関数 \(c:E \rightarrow \mathbb{R}_{\geq 0}\) が与えられたとき、カットの容量 (capacity) が \(S\) から \(T\) に向かう辺の容量の和として定義されます: \[ \| S, T \| = \sum_{s \in S} \sum_{t \in T} c(s \rightarrow t) \] (ここでも辺 \(v \rightarrow w\) が存在しない場合には \(c(v \rightarrow w) = 0\) とします) この定義が非対称なことに注意してください。\(T\) から \(S\) に向かう辺はカウントしません。
最小カット問題 (minimum cut problem) とは、容量が最小の \((s,t)\)-カットを計算する問題です。
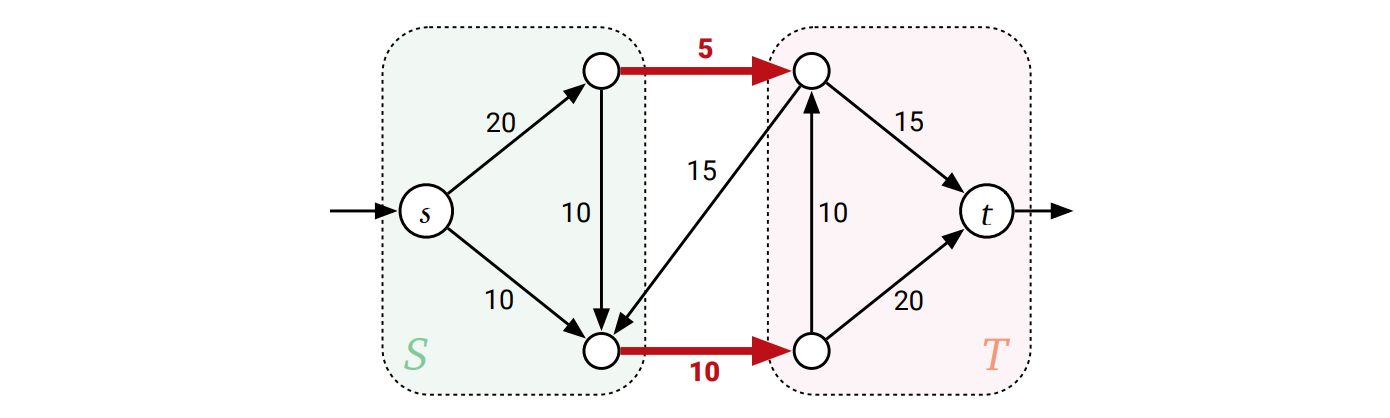
直感的に言えば、最小カットとは \(s\) から \(t\) への全てのフローを断ち切るための一番安価な方法です。フローとカットに関する次の関係を示すのは難しくありません:
命題 10.1 \(f\) を実現可能な任意の \((s,t)\)-フロー、\((S, T)\) を任意の \((s, t)\)-カットとする。このとき \(f\) の値は \((S, T)\) の容量以下である。また \(f\) が \(S\) から \(T\) へ向かう辺を全て飽和させてかつ \(T\) から \(S\) への全ての辺を避けることは \(|f| = \| S, T \|\) と同値である。
証明 任意の実現可能なフロー \(f\) とカット \((S, T)\) を取ると、次の不等式が成り立つ: \[ \begin{aligned} |f| & = \partial f (s) & [\text{定義}] \\ & = \sum_{v \in S} \partial f(v) & [\text{保存条件}] \\ & = \sum_{v \in S}\sum_{w} f(v \rightarrow w) - \sum_{v \in S} \sum_{u} f(u \rightarrow v) & [\partial \text{ の定義}] \\ & = \sum_{v \in S}\sum_{w \notin S} f(v \rightarrow w) - \sum_{v \in S} \sum_{u \notin S} f(u \rightarrow v) & [S \text{ から } S \text{ への辺を削除}] \\ & = \sum_{v \in S}\sum_{w \in T} f(v \rightarrow w) - \sum_{v \in S} \sum_{u \in T} f(u \rightarrow v) & [\text{カットの定義}] \\ & {\color{red}\leq} \sum_{v \in S}\sum_{w \in T} f(v \rightarrow w) & [f(u \rightarrow v) \geq 0] \\ & {\color{red}\leq} \sum_{v \in S}\sum_{w \in T} c(v \rightarrow w) & [f(u \rightarrow v) \leq c(v \rightarrow w)] \\ & = \|S, T \| & [\text{定義}] \end{aligned} \]
二つ目のステップでは、全ての頂点 \(v \in S \backslash \lbrace s \rbrace\) において \(\partial f(v) = 0\) なことからゼロを足しているだけである。また四つ目のステップでは全ての \(x, y \in S\) に対するフローの値 \(f(x \rightarrow y)\) を削除しているが、これが可能なのはこの値が二つの和の両方で出現するためである。つまり、\(v = x\) と \(w = y\) のときに一度、\(v = y\) と \(u = x\) のときに一度出現する。
式変形中の最初の不等号は \(f\) が \(T\) から \(S\) への辺を全て避けるときに限って等号となる。同様に二つ目の不等号は \(f\) が \(T\) から \(S\) への辺を全て飽和させるときに限って等号となる。 \(\Box\)
この命題から、もし \(|f| = \| S, T \|\) ならば \(f\) が最大フローで \((S, T)\) が最小カットであることが分かります。