最長増加部分列

任意の列 \(S\) に対して、\(S\) からゼロ個以上の要素を削除してできる列を部分列 (subsequence) と言います。このとき残った要素の順番は変更せず、部分列の要素は \(S\) で隣り合っている必要はありません。

例えば街の大通りを車で通って信号の列 \(S\) を通り過ぎるとき、あなたが車を停めるのは赤になっている信号からなる \(S\) の部分列です。運が良ければ信号で全く停まらずに済みますが、その場合に対応する空列も \(S\) の部分列です。また運が悪くて全ての信号につかまった場合に対応する \(S\) 自身も \(S\) の部分列となります。

もう一つ例をあげると、\(\color{maroon}{\texttt{BENT}}\), \(\color{maroon}{\texttt{ACKACK}}\), \(\color{maroon}{\texttt{SQUARING}}\), \(\color{maroon}{\texttt{SUBSEQUENT}}\) は全て \(\color{maroon} \texttt{SUBS} \)\( \color{maroon} \texttt{EQUE} \)\( \color{maroon} \texttt{NCEB} \)\( \color{maroon} \texttt{ACKT} \)\( \color{maroon} \texttt{RACK} \)\( \color{maroon} \texttt{ING}\) の部分列であり、空文字列と \(\color{maroon}\texttt{SUBS} \)\( \color{maroon} \texttt{EQUE} \)\( \color{maroon} \texttt{NCEB} \)\( \color{maroon} \texttt{ACKT} \)\( \color{maroon} \texttt{RACK} \)\( \color{maroon} \texttt{ING}\) 自身もそうです。また \(\color{maroon} \texttt{QUEUE}\), \(\color{maroon} \texttt{EQUUS}\), \(\color{maroon} \texttt{TALLYHO}\) はどれも部分列ではありません。部分列であってその要素が元の列において連続しているものを、部分文字列 (substring) と言います。例えば \(\color{maroon}{\texttt{MASHER, LAUGHTER}}\) はどちらも \(\color{maroon}{\texttt{MANSLAUGHTER}}\) の部分列ですが、部分文字列なのは \(\color{maroon}{\texttt{LAUGHTER}}\) だけです。

整数列が与えられたときに、要素が昇順に並んでいる部分列で一番長いものを見つける問題を考えます。きちんと言うと、\(A[1..n]\) が与えられたときに、 全ての \(k\) に対して \(A[i_{k}] < A[i_{k+1}]\) が成り立つ添え字の列 \(1 \leq i_{1} < i_{2} < \cdots < i_{l} \leq n\) で一番長いものを求める問題です。

この最長増加部分列 (longest increasing subsequence) 問題に対する自然なアプローチは、\(1\) から \(n\) までの添え字 \(j\) について、\(A[j]\) が最長増加部分列に入るかどうかを決断していくというものです。処理の途中に放り込まれたところを想像すると、次の図のようになります:

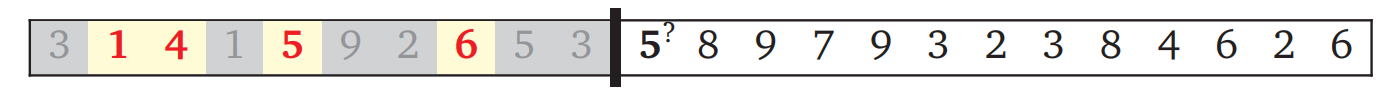
分かち書き問題の例と同じように、これまでの決断と未処理の入力が黒いバーで分かれています。出力の部分列に入れるように決断した数がハイライトされ、除外された数はグレーになっています (部分列に入れた数が昇順なことに注意してください！)。アルゴリズムが決断するのはバーのすぐ後ろの数を部分列に入れるかどうかです。

この例では次の数字 \(5\) が最後に選択した数字 \(6\) よりも小さいので、次の数字を部分列に入れることはできません。そのためそのまま次の決断に進みます:

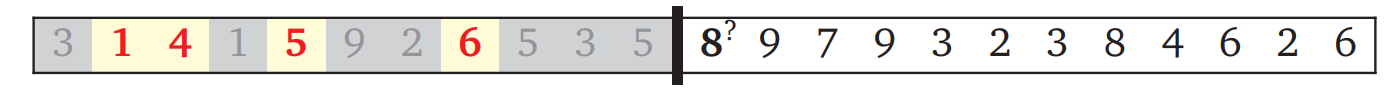
この状況では \(8\) を部分列に入れられますが、そうすべきかは分かりません。ここでもバックトラッキングを使ったアルゴリズムは "賢く" ならず、総当たりを使います:

• まず暫定的に \(8\) を部分列に入れる。そして再帰の妖精に残りの決断を任せる。
• 次に暫定的に \(8\) を部分列から外す。そして再帰の妖精に残りの決断を任せる。

長い部分列を返した方を選択します。これは部分和問題を解くときに使った再帰的なパターンと全く同じです。

続いて鍵となるこの問題を考えます: 「これまでの決断について覚えるべき情報は何か？」 \(A[j]\) を部分列に入れられるのは出来上がる部分列が昇順に並ぶときだけです。これまでの決断の結果から定義される \(A[1..j-1]\) の部分列は (帰納法により！) 昇順なので、\(A[j]\) を入れられるのは選択した \(A[1..j-1]\) の部分列の最後の要素よりも \(A[j]\) が大きいときだけです。したがって、過去について記憶しておくべき情報は最後に選択した数となります。この事実を使うと、前述の図から必要のない情報を取り除けます:

よって再帰的な戦略が実際に解くべきなのは次の問題です:

いつも通り、この再帰的な戦略にはベースケースが必要です。この戦略は配列の終端まで進むと "次の要素" が存在しなくなってそれ以上進めなくなるからです。空配列の部分列は空配列だけであり、「配列の要素が全て昇順に並んでいる」という命題が空配列に対して真であるために、空配列は増加列です。したがってベースケースである空配列の最長増加部分列の長さは \(0\) です。

以上の説明から、次のアルゴリズムが得られます:

ここで思い出してほしいのですが、配列を直接コールスタックに積むのは時間がかかる処理なのでした。そこで高速化のために、 \(A[1..n]\) をグローバル変数として配列の添え字を使って同じ処理をする方法を考えます。整数 \(\mathit{prev}\) は配列の要素 \(A[i]\) と表すことができ、再帰呼び出しに渡される配列の接尾部分は \(A[j..n]\) と表すことができます。したがって前述の再帰的な問題を添え字を使って次のように変形できます:

全ての要素が \(A[i]\) よりも大きい \(A[j..n]\) の部分列の中で一番長いものの長さを \(\mathit{LISBigger}(i, j)\) とすると、前述の再帰的な戦略から次の再帰方程式が得られます: \[ \mathit{LISBigger}(i, j) = \begin{cases} 0 & \text{if } j > n \\ \mathit{LISBigger}(i, j + 1) & \text{if } A[i] \geq A[j] \\ \max \left\lbrace \begin{array}{c} \mathit{LISBigger} (i, j + 1) \\ 1 + \mathit{LISBigger}(j, j + 1) \end{array} \right\rbrace & \text{それ以外} \end{cases} \] もし疑似コードがお好みなら:

最後に、このアルゴリズムを使って制約の無い元の問題を解きます。配列の最初に門番 (sentinel) として \(-\infty\) を追加するのが一番簡単です:

\(\textsc{LisBigger}\) の実行時間は Hanoi の塔と同じ再帰方程式 \(T(n) \leq 2\ T(n-1) + O(1)\) を満たし、\(T(n) = O(2^{n})\) です。この結果は驚くべきことではありません。というのも、最悪ケースにおいてこのアルゴリズムは入力配列の \(2^{n}\) 個の部分列全てを調べるからです。