♥ 線形選択

クイックソートに関する議論の中で、ソートされていない配列から中央値を見つける処理が線形時間で行えると説明しました。この操作のためのアルゴリズムは 1970 年代に Manuel Blum (マヌエル・ブラム)、Bob Floyd (ボブ・フロイド)、Vaughan Pratt (ヴォーン・プラット)、Ron Rivest (ロン・リベスト)、Robert Tarjan (ロバート・タージャン) によって発見されました。彼らのアルゴリズムが扱ったのは \(n\) 要素の配列と整数 \(k\) を受け取って配列から \(k\) 番目に小さい要素を取り出すというもっと一般的な問題であり、この問題を解くアルゴリズムはクイックセレクト (quickselect)あるいは片腕のクイックソート (one-armed quicksort) と呼ばれます。クイックセレクトは Tony Hoare (トニー・ホーア) によって 1961 年に最初に発表されましたが、それは彼がクイックソートを発表した論文のクイックソートを説明したまさにそのページでのことでした。

クイックセレクト

一般的なクイックセレクトアルゴリズムはまずクイックソートと同じようにピボットを選び、\(\textsc{Partition}\) サブルーチンを使って配列を分割します。そして二つの配列のうち元の配列で \(k\) 番目に小さい要素を含む片方だけに対して再帰呼び出しを行います。疑似コードを次に示します。

このアルゴリズムには注目すべき特徴が二つあります。一つはクイックソートと同じようにアルゴリズムの正しさがピボットの選択に依存していない点。もう一つは中央値 (\(k = n/2\) のケース) だけを考えているにもかかわらず、この Hoare の再帰的な戦略はそれよりも一般的な問題を考えている点です: 入力配列 \(A[1..n]\) の中央値が小配列 \(A[1..r-1]\) あるいは \(A[r+1..n]\) の中央値と等しくなることはまずありません。

\(\textsc{QuickSelect}\) の最悪実行時間 \(T(n)\) は \(\textsc{QuickSort}\) と似た再帰方程式に従います。\(r\) が分からないとどちらの配列を再帰的に探索するかが分からないので、最悪の場合を調べなければなりません: \[ T(n) \leq \max_{1 \leq r \leq n} \left\lbrace T(r-1), T(n-r)\right\rbrace + O(n) \] 再帰的に解く問題の大きさを \(l\) と置けば、方程式を単純化できます: \[ T(n) \leq \max_{0 \leq l \leq n-1} T(l) + O(n) \]

選択されるピボットが常に配列の中で一番大きい (または一番小さい) 物であった場合、この再帰方程式は \(T(n) = T(n - 1) + O(n)\) であり、\(T(n) = O(n^{2})\) となります (再帰木は単純な路です)。

良いピボット

もし何らかのマジカルな方法で良いピボットを選ぶことができたなら、二次関数的な最悪ケースを回避できるはずです。ここで言う良いピボットとは、ある \(\alpha < 1\) を用いて \(l \leq \alpha n\) と書けるピボットです。この場合、再帰方程式は以下のように単純になります: \[ T(n) \leq T(\alpha n) + O(n) \] この方程式は幾何級数に展開されます。その級数は一番大きな項に支配されるので、\(T(n) = O(n)\) です (ここでも再帰木は単純な路です。実行時間 \(O(n)\) における定数部分は \(\alpha\) に依存します)。

言い換えると、中央値に近い値を線形時間で見つけることができるならば、本当の中央値も線形時間で特定できるということです。ここで必要になるのは中央値近似の妖精 (Approximate Median Fairy) です。 Blum-Floyd-Pratt-Rivest-Tarjan アルゴリズムは入力の配列の部分配列を注意深く選び、さらにその部分配列の中央値を選ぶことで、クイックセレクトの良いピボットを再帰的に計算します。中央近似値の妖精とは再帰の妖精が変装した姿だったのです！

詳しく見ていくと、このアルゴリズムはまず入力の配列を \(\lceil n/5 \rceil\) 個のブロックに分割します。各ブロックはちょうど 5 個の要素を持ちます(最後の要素は 5 個よりも少ないかもしれませんが、正の無限大を追加することで 5 個にします)。次に各ブロックの中央値を総当たりで求め、それらを新しい配列 \(M[1..\lceil n/5 \rceil]\) とします。そしてこの新しい配列の中央値を再帰的に計算します。最後にこの中央値たちの中央値 (median of medians, 疑似コードでは \(\mathit{mom}\)) をピボットとして片腕のクイックソートを行います。

\(\textsc{MomSelect}\) は再帰を二度使っており、それぞれで計算される値が異なります。最初の再帰ではピボット要素 \(\mathit{mom}\) が計算され、次の再帰ではそのピボットを使って小配列の一方から中央値が計算されます。

解析

なぜこのアルゴリズムは高速なのでしょうか？ 鍵となるのは、中央値たちの中央値が良いピボットであるという事実です。\(\mathit{mom}\) は \(\lfloor n/5 \rfloor\) 個あるブロックごとの中央値たちの \(\lfloor \lceil n/5 \rceil / 2\rfloor - 1 \approx n / 10\) 個よりも大きく、そして各ブロックの中央値はそのブロックの中の二つの要素よりも大きいので、\(\mathit{mom}\) は入力の配列の少なくとも \(3n / 10\) 要素よりも大きくなります。同様に \(3n/10\) 要素よりも小さいことも言えます。したがって、二回目の再帰呼び出しは最大でも配列の \(7n/10\) しか探索しません。

入力の配列を \(5 \times \lceil n/5 \rceil\) の格子に描くとこのアルゴリズムの振る舞いが分かりやすくなります。ここで各列は五つの連続する要素からなるブロックです。図を分かりやすくするために、列の要素を上から下にソートし、さらに列ごとの中央値で列をソートしておきます (アルゴリズムではこの二番目のソートをしないことに注意してください)。こうした場合、中央値たちの中央値は格子の中心に一番近い要素となります。

格子の左上の要素が \(\mathit{mom}\) よりも小さい \(3n / 10\) 個の要素を示します。探索している要素が \(\mathit{mom}\) よりも大きい場合、この \(3n/10\) 個の要素は以降の探索から除外されます。そのため再帰的な小問題の入力サイズは最大でも \(7n/10\) となります。同様に探索している要素が \(\mathit{mom}\) よりも小さい場合には \(\mathit{mom}\) よりも大きい \(3n/10\) 個の要素が探索から除外されます。つまり再帰的に解く小問題のサイズは必ず \(7n / 10\) 以下です。

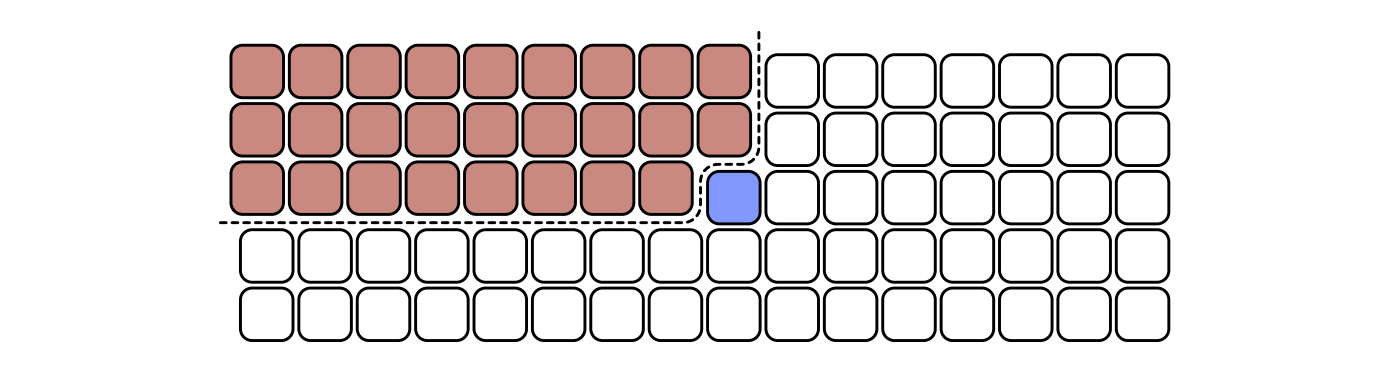
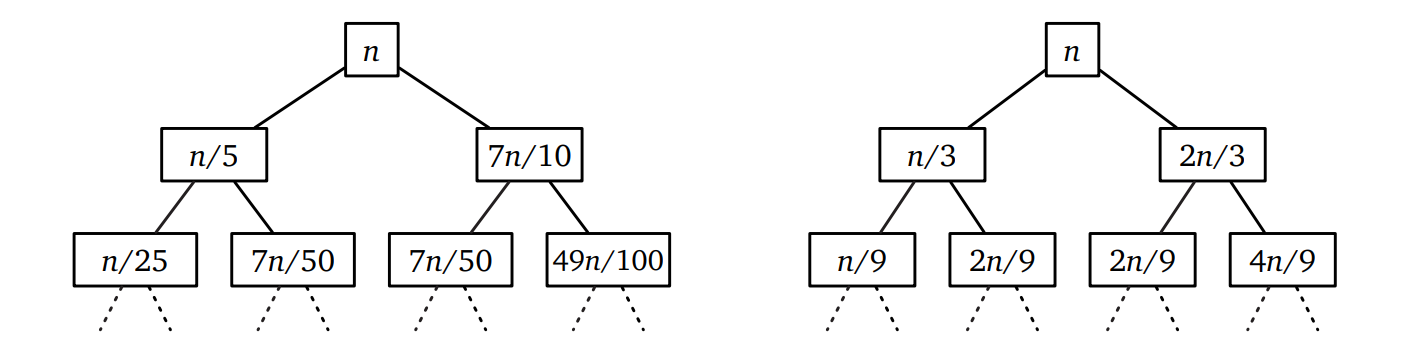
これで \(\mathit{mom}\) が良いピボットであることはわかりました。しかしこのアルゴリズムは二つの再帰呼び出しをしています。どうすればこれが線形時間だと証明できるでしょうか？ ここで鍵となるのは、再帰的に解く二つの小問題のサイズの和が入力のサイズよりも定数倍で小さいという事実です。このアルゴリズムの最悪計算時間は次の再帰方程式を満たします: \[ T(n) \leq T(n/5) + T(7n/10) + O(n) \]

この再帰方程式に対応する再帰木を描くと、高さごとの値の和が一つ上の値の和の \( 9 / 10 \) 以下であることが分かります。したがって高さごとの値の和の合計は減少幾何級数であり、解は \(T(n) = O(n)\) です (ここでも再帰木のバランスが取れていませんが、何の問題もありません)。やったぜ！ Thanks, Mom!

サニティチェック

ここまでくると、多くの生徒がマジックナンバー 5 について質問をしてきます。なぜこの数字を選んだのですか、と。その質問に対する答えは「実行時間を表す和が減少幾何級数となる最小の奇数が 5 だから」です (ブロックのサイズを偶数にすると手続きが複雑になります)。仮にブロックのサイズを 3 とすると、実行時間が満たす再帰方程式は次のようになります: \[ T(n) \leq T(n/3) + T(2n/3) + O(n) \] この再帰方程式には見覚えがあります！この場合、再帰木の高さごとの値の和は常に \(n\) 以下です。再帰木の葉の高さは同じではありませんが、上界を求めるために一番深い葉の高さ \( \log_{3 / 2} n \) を考えると、再帰木全体の値は最大 \( n \log_{3 / 2} n = O(n \log n) \) です。したがって再帰方程式の解として \(T(n) \leq O(n \log n)\) が得られます。一方で一番浅い葉の高さは \(\log_{3} n\) なので、この上界を定数倍以上に改善することはできません。よって三分割による中央値の中央値選択はソートと同じ速さとなってしまいます。

アルゴリズムをさらに詳細に解析すると、比較演算だけを考えたとしても \(O()\) 表記で隠される定数部分が非常に大きいということが分かります。5 要素の配列の中央値を求めるには比較が最大 6 回必要となるので、再帰的な小問題を組み立てるのには最大 \( 6n / 5\) 回の比較が必要になります。その再帰呼び出しの後の分割処理はナイーブに実装すれば \(n - 1\) 回の比較が必要になります。ただし分割を行う時点で配列の要素のうち \( 3n / 10\) 個はピボットとの大小が分かっているので、追加で必要となる比較は \(2n / 5\) 回となります。したがって、最悪ケースの比較演算の回数に関する再帰方程式は次のようになります: \[ T(n) \leq T(n / 5) + T(7n / 10) + 8n / 5 \] 再帰木の方法を使うと、上界が求まります: \[ T(n) \leq \frac{8n}{5} \sum_{i \geq 0} \left(\frac{9}{10}\right)^{i} = \frac{8n}{5} \cdot 10 = 16n \] 実際に中央値の中央値アルゴリズムを動かすとこの最悪ケースほどはひどくなりません ――全ての再帰呼び出しで最悪ケースを引く確率はとても低いからです―― が、常識的に十分大きいとみなされるような配列においてさえ、ソートよりも遅くなることがあります¹。

1. 実は、ピボットの実用上正しい選び方は一様ランダムに選ぶことです。この方法では中央値を見つけるために必要となる比較演算の回数の期待値が \(4n\) となります。詳細は乱数アルゴリズムについての私の講義ノート http://algorithms.wtf を参照してください。^[return]