練習問題

読者への注意: 貪欲アルゴリズムを使って解けない問題が混じっています！ また貪欲アルゴリズムを説明、解析するときには正しさの証明を必ず付けてください。証明は通常交換の議論の形をしているはずです。普通の問題では正しさの証明を要求しない (私の担当しているような) 講義において、この証明は特に重要となります。

講義のスケジューリング問題に対する $\textsc{GreedySchedule}$ アルゴリズムは、この問題に対する唯一の貪欲アルゴリズムであるというわけではありません。このアルゴリズムとは異なる貪欲な戦術をいくつか次に示します。それぞれについて、その戦術が常に最適なスケジュールを生成するならそのことを証明し、そうでないなら最適なスケジュールが出力されない入力のうちできる限り小さいものを示してください。アルゴリズムの途中で同着の講義が生じた場合にはランダムに選択する (あなたが選択を管理することはできない) と仮定してください。 [ヒント: 正しいアルゴリズムは三つだけです。]
1. 最も遅く終わる講義 $x$ を選び、$x$ と衝突する講義を除去し、再帰的に処理する。
2. 最も早く始まる講義 $x$ を選び、$x$ と衝突する講義を除去し、再帰的に処理する。
3. 最も遅く始まる講義 $x$ を選び、$x$ と衝突する講義を除去し、再帰的に処理する。
4. 最も短い講義 $x$ を選び、$x$ と衝突する講義を除去し、再帰的に処理する。
5. 衝突する講義の数が一番少ない講義 $x$ を選び、$x$ と衝突する講義を除去し、再帰的に処理する。
6. 考えている講義に衝突が無いなら、それらを全て選んで終了。そうでないなら、一番長い講義を除去して再帰的に処理する。
7. 考えている講義に衝突が無いなら、それらを全て選んで終了。そうでないなら、衝突する講義が最も多い講義 $x$ を除去して再帰的に処理する。
8. 一番早く始まる講義を $x$ 、二番目に早く始まる講義を $y$ とする。
  - $x$ と $y$ が衝突しないなら、$x$ を選んで $x$ 以外の講義について再帰的に処理する。
  - $x$ が $y$ を完全に含むなら、$x$ を除去して再帰的に処理する。
  - それ以外の場合は、$y$ を除去して再帰的に処理する。
9. ある講義 $x$ の時間が他の講義の時間を完全に含むなら、$x$ を除去して再帰的に処理する。そのような講義が無いなら、最も遅く終了する講義 $y$ を選び、$y$ と衝突する講義を取り除き、再帰的に処理する。
重み付きの講義スケジューリング問題を考えます。各講義はそれぞれ単位時間 (講義の時間とは無関係) を持っており、衝突しない講義の集合で単位時間を最大化するものの計算が目標です。入力は講義の開始時間、終了時間、単位時間を表す三つの配列です。
1. この章の最初に説明した貪欲アルゴリズム ――一番早く終わるものを選んで再帰的に処理する―― が常に最適なスケジュールを返すわけではないことを示してください。
2. 練習問題 4.1 で説明したアルゴリズムはどれも常に最適なスケジュールを返すわけではないことを示してください。 [ヒント: 練習問題 4.1 を先に解いてください。この問題で上手く行かないアルゴリズムはここでも上手く行きません。]
3. 常に最適なスケジュールを計算するアルゴリズムを説明、解析してください。 [ヒント: 答えは貪欲アルゴリズムではありません。]
数直線上の $n$ 個の区間の集合を $X$ とします。 $X$ の部分集合 $Y$ が $X$ を覆う (cover する) とは、$Y$ に含まれる区間の和集合が $X$ に含まれる区間の和集合と等しいことを言います。$X$ を覆う $X$ の部分集合で最小のものを計算する効率の良いアルゴリズムを説明、解析してください。入力は $X$ に含まれる区間の始点と終点を表す配列 $L[1..n]$ と $R[1..n]$ とします。もし貪欲アルゴリズムを使うなら、その正しさを必ず証明してください。

区間の集合とそれを覆う大きさ $7$ の部分集合 (色の付いている区間)
数直線上の $n$ 個の区間の集合を $X$ とします。数直線上の点の集合 $P$ が $X$ を貫く (stab する) とは、 $X$ に含まれる全ての区間が少なくとも一つの $P$ の点を含むことを言います。 $X$ を貫く最小の点集合を求める効率の良いアルゴリズムを説明、解析してください。入力は $X$ に含まれる区間の始点と終点を表す配列 $L[1..n]$ と $R[1..n]$ とします。もし貪欲アルゴリズムを使うなら、いつも通りその正しさを証明してください。

四つの点 (垂直な線分) で貫かれる区間の集合
数直線上の $n$ 個の区間の集合を $X$ とします。 $X$ の真の彩色 (proper coloring) とは、$X$ に含まれる全ての区間に対する色の割り当てであって重なり合うどの区間も同じ色で塗られないものを言います。 $X$ の真の彩色の持つ最小の色数を計算する効率の良いアルゴリズムを説明、解析してください。入力は $X$ に含まれる区間の始点と終点を表す配列 $L[1..n]$ と $R[1..n]$ とします。もし貪欲アルゴリズムを使うなら、いつも通りその正しさを証明してください。

区間の集合に対する五つの色を使った正しい彩色
1. 任意の整数 $n$ に対して、 Huffman 符号木の高さが $n-1$ となるような頻度配列 $f[1..n]$ であって最大の頻度が最小のものを求めてください。
2. 符号化前の文章の長さ $N$ がアルファベットのサイズ $n$ の多項式で抑えられているとします。この文章の頻度配列 $f[1..n]$ に対する Huffman 符号木の高さが $O(\log n)$ であることを示してください。
❤ 頻度配列 $f[1..n]$ が次の二つの条件を満たすとき、$\pmb{\alpha}$-heavy であると言います。
- 任意の $i > 1$ に対して $f[1] > f[i]$; つまり、記号 $1$ が狭義に最も頻度の高い記号である。
- $f[1] \geq \alpha \sum_{i=1}^{n} f[i]$; つまり、メッセージに含まれる全ての記号のうち、記号 $1$ の割合が $\alpha$ よりも大きい。
任意の $\alpha$-heavy な頻度配列に対する全ての Huffman 符号において文字 $1$ が一ビットで表されるような実数 $\alpha$ の最小値を求めてください。 [ヒント: まず $1 / 3 \leq \alpha \leq 1 / 2$ を示してください。]
与えられた頻度配列 $f[1..n]$ に対する最適な線形独立三進符号を求めるアルゴリズムを説明、解析してください。全ての $n$ に対して正しいことを示すのを忘れないでください。
先述したGale-Shapley のアルゴリズムの、最悪実行時間が $O(n^{2})$ である実装を詳細に説明してください。
1. Gale-Shapley のアルゴリズムが停止するまでに $\Omega(n^{2})$ 回のオファーを出すことがあり得ることを証明してください (アルゴリズムに対する実際の入力とそれに対する $\Omega(n^{2})$ 個の正しいオファーの列を示してください)。
2. 任意の $n$ に対して、Gale-Shapley のアルゴリズムを実行したときに各反復でどんなオファーが出されたとしても停止するまでに $\Omega(n^{2})$ 回の反復を要するような、$n$ 人の医師と $n$ 個の病院のランク付けを示してください。 [ヒント: (b) が示せれば自動的に (a) も示せます。]
与えられた医師と病院のランク付けに対する安定マッチングが唯一であるかどうかを判定する効率の良いアルゴリズムを説明、解析してください。
次の一般化した安定マッチング問題を考えます: 医師と病院は全ての病院/医師をランク付けせず、医師と病院がマッチするのはお互いがお互いをランク付けしているときだけとします。この条件では、マッチングが不安定となる状況が三つ加わります:
- マッチ相手がいる病院が、現在のマッチ相手よりもマッチせずに残っている医師を高くランク付けしている。
- マッチ相手がいる医師が、現在のマッチ相手よりもマッチせずに残っている病院を高くランク付けしている。
- マッチしていない医師とマッチしていない病院がお互いのランク付けに現れる。
この条件における安定マッチングでは、ランク付けが空でないにもかかららずマッチしていない医師や病院があっても構いません。例えば全ての医師が Harvard だけを一位にランク付けし、全ての病院が Dr. House だけを受け入れるインターンとしてランク付けした場合、Harvard と Dr. House だけがマッチされます。

この一般化された問題に対する安定マッチングを計算する効率の良いアルゴリズムを説明、解析してください。 [ヒント: 全ての医師と病院が互いをランク付けしているような小さいインスタンスに帰着させ、Gale-Shapley のアルゴリズムを使ってください。]
スカンジナビアの家具会社 Fürni は $n$ 個の同じ荷物をデラウェア州ウィルミントン内の $n$ 箇所の異なる住所に届けるために、$n$ 人のドライバーを雇いました。各ドライバーはウィルミントン内の $n$ 箇所の住所を回るこだわりの配送ルートを持っており、配送のときには必ずそのルートに従うとします。

何も条件が無ければ $n$ 人のドライバーが $n$ 個の住所のうちどこに荷物を届けても問題は無いのですが、厄介なことが起こりました。ドライバーの一人が全ての Johannshamn のソファ (Strinne グリーンストライプパターン入り) に近接センサーと爆弾を仕掛けたのです。二つのソファが同じ時間に同じ場所にあると、両方のソファは爆発し、配送トラックと建物を吹き飛ばしてしまいます。爆発が起こるのは二人のドライバーが同じ住所に荷物を届けた場合、あるいはあるドライバーがソファを届けたあとに他のドライバーがソファを持ったままその住所を訪れた場合です。

爆発が起きないようにドライバーに届け先住所を割り当てるのが Fürni の配送管理人としてのあなたの仕事です。 $n$ 個の住所が荷物を受け取り、かつ爆発が起きないようなドライバーの住所への割り当てを計算するアルゴリズムを説明してください。

例えば、 Jack のルートは 6 pm に 537 Paper Street 、8 pm に 1888 Franklin Street に訪れるものであり、 Marla のルートは 7 pm に 537 Paper Street 、 9 pm に 1888 Franklin Street を訪れるものだとします。このとき Jack は 1888 Franklin に、 Marla は 537 Paper に配送させるのが正解の割り当てとなります。そうでない割り当てでは 8 pm に 1888 Franklin で爆発が起きてしまいます (Cue the Pixies)。 [ヒント: Jack と Marla はある意味で不安定です。]
あなたは小さな商店の店主です。あなたの住んでいる国には $n$ 種類のコインがあり、それぞれの価値は $1 = c[1] < c[2] < \cdots < c[n]$ だとします (例えば合衆国では $n=6$ で $c = [1,5,10,25,40,100]$ です)。王室大蔵省で働く公務員たちが丹精込めて硬貨に刻んだ皆から愛される慈愛に満ちた元首 El Generalissimo の肖像をすり減らしてしまわないように、店員がお釣りを渡すときにはなるべく少ない枚数の硬貨を使わなければならないという法令が制定されています。
1. 合衆国では貪欲アルゴリズムを使うと必ず最小の数の硬貨を渡すことができます。つまり、お釣りの額を超えない最大の硬貨を渡し、残りの額について再帰的に同じことをするという方法です。El Generalissimo はこの資本主義的な貪欲さを気に入りませんでした。この貪欲アルゴリズムが最小の硬貨の集合を計算するのに失敗するようなコインの価値の集合を示してください。
2. El Generalissimo は決断を下し、硬貨の単位を整数の連続するべき $b^{0},$ $b^{1},$ $b^{2},$ $\ldots,$ $b^{k}$ $(b \geq 2)$ にするとしました。この通貨制度だと El Generalissimo が嫌う貪欲アルゴリズムを使って最適なお釣りを計算できてしまうことを示してください。
3. お釣りの額 $T$ とソートされた通貨の単位 $c[1..n]$ が与えられたときに、合計が $T$ となる最小の硬貨の集合を求める効率の良いアルゴリズムを説明、解析してください。 $c[1] = 1$ であってどんな $T$ に対してもちょうどお釣りを渡せるとします。
正でもゼロでも負でもありうる整数の配列 $A[1..n]$ が与えられたとします。 $A$ の連続する部分配列 $A[i..j]$ が正の区間 (positive interval) であるとは、その和がゼロより大きいことを言います。 $A$ に含まれる全ての正の整数を覆うような正の区間の集合の大きさの最小値を求めるアルゴリズムを説明、解析してください。例えば、以下の配列が与えられたときのアルゴリズムの出力は $3$ です。また入力配列が全て負だった場合の出力は $0$ です。
次の処理を考えます。最初 $x=1$ であり、各ステップで行えるのは $x$ を $1$ 増やす increment と二倍する doubling のどちらかです。目標は整数 $n$ を作ることです。例えば、$10$ は次の 4 ステップで作ることができます: \[ 1 \overset{+1}{\longrightarrow} 2 \overset{\times 2}{\longrightarrow} 4 \overset{+1}{\longrightarrow} 5 \overset{\times 2}{\longrightarrow} 10 \] $n$ を $n-1$ 回の increment で作ることができるのは明らかですが、ほとんどの $n$ についてもっと効率的な作り方があります。与えられた整数 $n$ を作るための最小ステップ数を計算するアルゴリズムを説明、解析してください。
$n$ 人のスキーヤーの背の高さが配列 $P[1..n]$ で表され、$n$ 個のスキー板の長さが配列 $S[1..n]$ で表されるとします。スキー板とスキーヤーの高さの差の平均値が最小になるようにスキー板をスキーヤーに割り当てるアルゴリズムを説明、解析してください。アルゴリズムが計算するのは置換 $\sigma$ であって次の値を最小にするものです: \[ \frac{1}{n} \sum_{i=1}^{n} |P[i] - S[\sigma[i]]| \]
Alice はパーティを開くことになり、誰を招待しようか考えています。彼女には招待できる知り合いが $n$ 人いて、そのうち誰と誰がお互いに知り合いであるかを彼女は知っています。 Alice は次の制約の下でなるべく多くの人を招待することにしました:
- どの招待客も他の招待客の中に少なくとも 5 人の知り合いがいる。
- どの招待客も他の招待客の中に少なくとも 5 人の知り合いでない人がいる。
Alice が招待できる最大の人数を計算するアルゴリズムを説明、解析してください。アルゴリズムの入力は $n$ 人の名前と誰と誰が知り合いかを表す名前の組の配列です。
二つの正の整数の配列 $R[1..n]$ と $C[1..n]$ が与えられたとします。要素が $0$ または $1$ である $n \times n$ の行列が $R$ と $C$ の組と適合 (agree) するとは、全ての添え字 $i$ について $i$ 行目が $R[i]$ 個の $1$ を含み、$i$ 列目が $C[i]$ 個の $1$ を含むことを言います。$R$ と $C$ が与えられたときに、適合する行列を構築するか、適合する行列が存在しないならばそのことを正しく報告するアルゴリズムを説明、解析してください。
あなたはブリトーをサンフランシスコからニューヨークまで配達する仕事を Elon Musk から受託しました。あなたはブリトー配達車両を運転して最近 Elon が建設した大陸横断ブリトー配達地下トンネル¹を走ることになります。このトンネルは二つの都市を直線で結んでいます。

ブリトー配達車両には使い捨てのバッテリーがついており、100 マイル走るごとに取り換えなければなりません。燃料は実質無料なのですが、バッテリー自体が高価で壊れやすいために、バッテリーの交換作業を行えるのは大陸横断ブリトー配達地下トンネル車両バッテリー交換連合の正規職員²だけです。そのためバッテリーの残量がまだあったとしても、新しいバッテリーに交換すると料金が満額かかります。加えてあなたの車両はとても小さいので、予備のバッテリーを載せておくことができません。

トンネル内にはいくつか燃料補給所があり、場所によってバッテリーの交換にかかる料金が異なります。旅を始めるに先立って、あなたはトンネル内の全ての燃料補給所とそこでのバッテリー交換料金をリストにした Wikipedia ページを印刷しておきました。どこで燃料を補給するかをどうやって決めればよいでしょうか？

きちんと言うと、こうなります: 二つの配列 $D[1..n]$ と $C[1..n]$ が与えられ、$D[i]$ がトンネルの入口から $i$ 番目の燃料補給所までの距離を表し、$C[i]$ が $i$ 番目の燃料補給所でバッテリーを交換したときにかかる料金を表しているとします。あなたの旅は最初の燃料補給所から始まって最後の燃料補給所で終わり (つまり $D[1]=0$ で、$D[n]$ が旅の総距離を表し)、最初車両には燃料が入っていない (一番目の燃料補給所には必ず停まる) とします。
1. 旅を完了するために停車すべき燃料補給所の数の最小値を求める貪欲アルゴリズムを説明、解析してください。アルゴリズムが正しいことの証明を忘れないでください。
2. 本当に最小化したいのは停車する燃料補給所の数ではなく全体のコストです。(a) の貪欲アルゴリズムが常に最適な解を出力するわけではないことを示してください。
3. 旅の全体コストを最小化する場合に、停車すべき燃料補給所を計算する効率の良いアルゴリズムを説明してください。
あなたは $n$ 冊の本を保管する図書館に雇われました。本は索引システムに基づいて一列に並んでおり、この順番を変えることはできません: つまり、全ての棚は並んだ本の連続する一区間だけを保存できます。二つの配列 $H[1..n]$ と $T[1..n]$ が与えられ、$H[i]$ と $T[i]$ がそれぞれ $i$ 個目の本の高さと厚さを表しているとします。図書館にある全ての棚は同じ幅 $L$ を持ち、棚に入っている本の厚さの合計は $L$ を超えてはいけません。
1. 全ての本の高さが $h$ で、棚の高さは $h$ よりも大きいとします。このときどの本も棚に並べられます。最小限の棚を使って全ての本を棚に入れる貪欲アルゴリズムを説明、解析してください。 [ヒント: アルゴリズムは明らかです。でもなぜそれが正しいのでしょうか？]
2. いい準備運動でしたね。さぁ本物の問題を考えましょう。現実の図書館にある棚は異なる高さを持ちます。ただしその高さは調整でき、棚に収められている本の高さの最大値になるまで棚を低くできます (空の棚の高さを 0 にすることもできます)。棚の高さの合計が最小になるように本を棚に収めるのがあなたの仕事です。(a) の貪欲アルゴリズムが常に最適な解を出力するわけではないことを示してください。
3. (b) で説明された棚に対する最良の本の収め方を見つけるアルゴリズムを説明、解析してください。
丸括弧 $\color{green}{(}$ と $\color{#B52F1B}{)}$ からなる文字列 $w$ のバランスが取れているとは、次の条件のどれかを満たすことを言います:
- $w$ は空文字列である。
- あるバランスの取れた文字列 $x$ を使って $w = {\color{green}(} x \color{#B52F1B}{)}$ と表せる。
- あるバランスの取れた文字列 $x,y$ を使って $w = xy$ と表せる。
例えば文字列 \[ w = {\color{green}{(}}{\color{green}{(}}{\color{green}{(}}{\color{#B52F1B}{)}}{\color{#B52F1B}{)}}{\color{green}{(}}{\color{#B52F1B}{)}}{\color{green}{(}}{\color{#B52F1B}{)}}{\color{#B52F1B}{)}}{\color{green}{(}}{\color{green}{(}}{\color{#B52F1B}{)}}{\color{green}{(}}{\color{#B52F1B}{)}}{\color{#B52F1B}{)}}{\color{green}{(}}{\color{#B52F1B}{)}} \] はバランスが取れています。なぜなら次のように $x, y$ を定義すると $w = xy$ であり、 $x$ と $y$ はバランスが取れているからです。 \[ x = {\color{green}{(}}{\color{green}{(}}{\color{green}{(}}{\color{#B52F1B}{)}}{\color{#B52F1B}{)}}{\color{green}{(}}{\color{#B52F1B}{)}}{\color{green}{(}}{\color{#B52F1B}{)}}{\color{#B52F1B}{)}},\quad y = {\color{green}{(}}{\color{green}{(}}{\color{#B52F1B}{)}}{\color{green}{(}}{\color{#B52F1B}{)}}{\color{#B52F1B}{)}}{\color{green}{(}}{\color{#B52F1B}{)}} \]
1. 丸括弧からなる文字列が与えられたときに、その文字列のバランスが取れているかを判定するアルゴリズムを説明、解析してください。
2. 丸括弧からなる文字列が与えられたときに、その文字列に含まれるバランスの取れた部分列で最長のものの長さを計算する貪欲アルゴリズムを説明、解析してください。いつものように、正しさの証明を忘れないでください。
両方の問題について入力は $w[1..n]$ であり、$w[i] = \color{green}{(}$ または $w[i] = \color{#B52F1B}{)}$ だとします。両方のアルゴリズムの実行時間は $O(n)$ になるはずです。
ある日、ジムの壁を登るのに飽きた Alex はクライマーの友達を大勢誘って屋外の壁を登りに行きました。彼らが訪れたクライミングエリアはとても横にとても長い岩で、あまり高くはありませんでした。岩には手足を掛ける場所 (ホールド) がたくさんありましたが、それを見た Alex は友達と話し合って、"許されている" 動きを設定しました。次のホールドに移動するときには、このルールに従わなければなりません。

ホールドと許されている動きは $n$ 頂点の根付き木 $T$ で表され、頂点がホールドに、辺が許されているホールド間の動きを表します。岩を上る道は上に行くほど小さくなり、最終的にホールド一つになります。このホールドが $T$ の根に対応します。

Alex とその友達 (みな優秀なクライマーです) はなるべく多い人数で岩を同時に上るというゲームをすることになりました。ただしクライマーはちょうど $k$ 回だけ岩を上に向かって登らないといけません。つまり、クライマーは $T$ の中で根に向かって長さ $k$ の道を描きます。加えて、一つのホールドを使えるのは一人のクライマーだけです。つまりクライマーの軌跡が交差してはいけません。
1. このゲームをプレイできる最大人数を計算する貪欲アルゴリズムを説明、解析してください。アルゴリズムの入力は根付き木 $T$ と整数 $k$ であり、出力は $T$ の根に向かう長さ $k$ の互いに重ならない $T$ の路からなる集合の最大の大きさです。 $T$ が二分木だと仮定しないでください。次の例では $k=3$ であり、アルゴリズムの出力は整数 $8$ です。
  
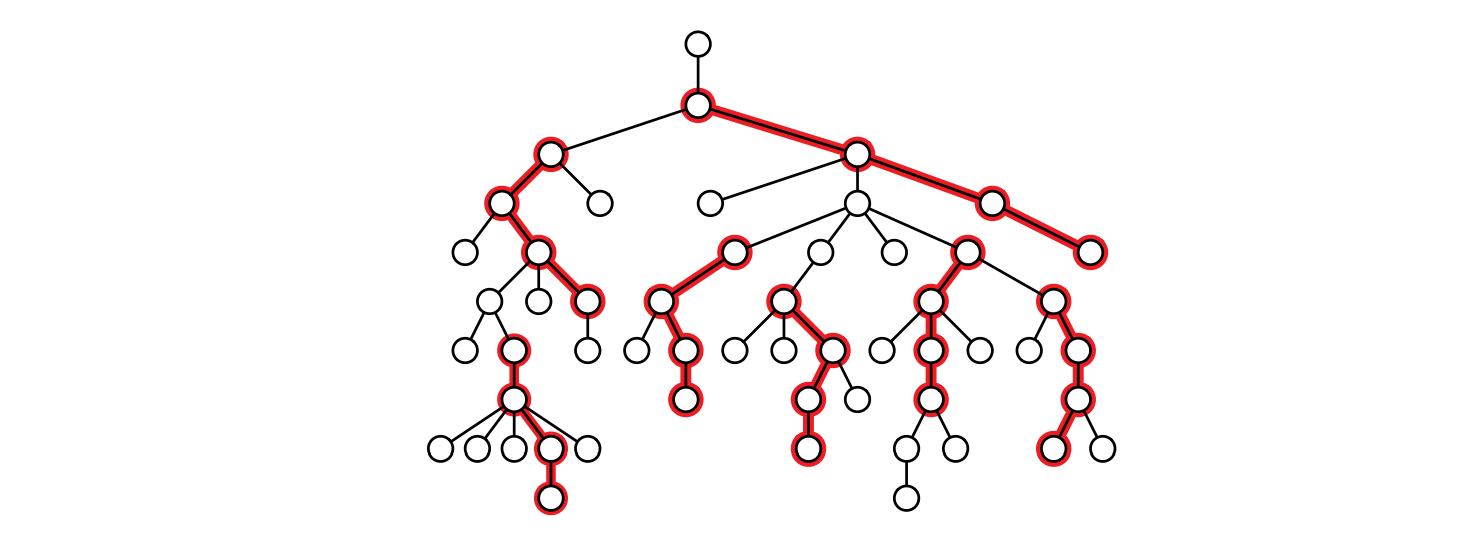  $長さが $k=3$ である重ならない 7 つの道 (これはこの木で条件を満たす最大の道の集合ではない)$
  
  図 4.6
  
  長さが $k=3$ である重ならない 7 つの道 (これはこの木で条件を満たす最大の道の集合ではない)
2. $T$ の頂点に報酬が付いているとします。この問題の目標は道の集合の大きさではなく道の集合に含まれる頂点の報酬の和を最大化することです。(a) の貪欲なアルゴリズムが常に最適な報酬を返すわけではないことを示してください。
3. (b) で説明した報酬の最大値を計算する効率の良いアルゴリズムを説明してください。
おめでとうございます！あなたは Camelot を征服しました！腐敗しきった世襲君主制は無政府組合主義のコミューンにとって代わり、市民は順番に "今週の行政官" となり、重要な決断は隔週の特別な会議で行われ、純粋に内政に関するものは過半数の賛成で、そうでない重要なものは三分の二の賛成をもって...

この征服を締めくくる象徴的な行為として、あなたは円卓 (驚くことに本当に丸い机でした) をピザのように楔形に切って、戦利品として Camelot の市民に配ることにしました。あなたは全ての市民に対して円卓のどの角度が欲しいかを聞いて回り、市民の要求を二つの角度としてまとめました。例えば Sir Robin the Brave は $17.23^{\circ}$ から $42^{\circ}$ を、 Sir Lancelot the Pure は $359^{\circ}$ から $1^{\circ}$ (の二度)を、などです。市民は要求とちょうど同じ形を受け取らない限り満足しませんが、市民の要求は重なっているので全員を満足させるのは不可能です。政治へようこそ。

満足させることができる市民の数の最大値を計算するアルゴリズムを説明、解析してください。角度が整数だと仮定しないでください。 [ヒント: アルゴリズムの出力はテーブルを回転させても変わらないはずです。]
あなたは巨大な風船に取り囲まれていて、手には真新しい Acme 印の Zap-O-Matic™ を握っています。 Zap-O-Matic™ を撃つと直進する高エネルギーレーザービームが放たれ、進路上にある風船が全て割れます。現在位置から移動することなく Zap-O-Matic™ を使って全ての風船を割るのがあなたの目標です。ただしこの銃は一発撃つのに小国が一年で消費するのと同じぐらいの電力を必要とするので、なるべく少ない銃撃で全ての風船を割らなくてはなりません。

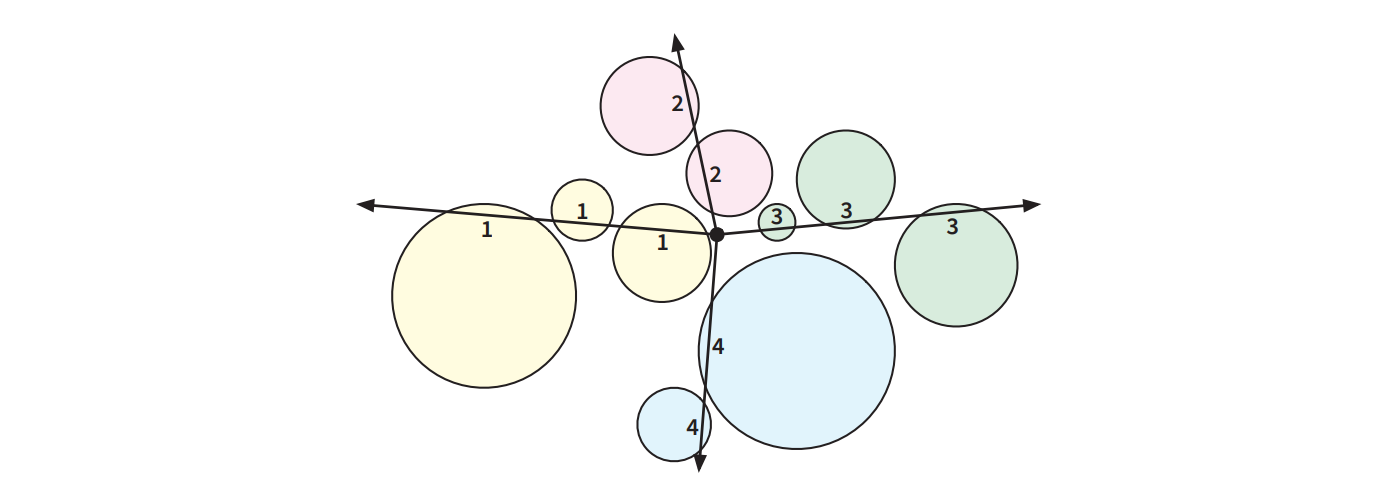図 4.7

Zap-O-Matic™ の四回の銃撃で割られる 9 個の風船

この最小 zap 問題は次のように定義できます: 「平面上の $n$ 個の円の集合 $C$ が与えられ、円が中心座標 $(x, y)$ と半径で表されるときに、原点を始点とするレイ (半直線) の集合であって全ての円がどれかと交わるものの大きさの最小値を求めよ」この問題に対する効率の良いアルゴリズムを見つけるのがこの練習問題の目標です。
1. どの風船とも交差しないレイを放つことができるとします。この最小 zap 問題の特殊ケースに対する貪欲アルゴリズムを説明、解析してください。 [ヒント: 練習問題 4.2]
2. 最適解との差が $1$ 以内であるような答えを出力する貪欲アルゴリズムを説明、解析してください。つまり、最適の場合 $m$ 個のレイで全ての風船を割ることができるときに、出力が $m$ または $m+1$ となる貪欲アルゴリズムを答えてください (もちろんこの事実を証明してください)。
3. 最小 zap 問題を $O(n^{2})$ 時間で解くアルゴリズムを説明してください。
4. ❤ 最小 zap 問題を $O(n \log n)$ 時間で解くアルゴリズムを説明してください。
任意の円 $c$ と交わるレイの角度の範囲を $O(1)$ で計算できるサブルーチンが利用可能であるとしてください。このサブルーチンを実際に書くのは難しくありませんが、これを実際に書くことがこの問題の狙いではありません。

このトンネルが参考にしたのはもちろん、Maciej Cegłowski が構想した Alameda-Weehauken ブリトートンネルです (https://idlewords.com/2007/04/the_alameda_weehawken_burrito_tunnel.htm)。^[return]
ドイツ語で言うなら Die Transkontinentaluntergrundburritolieferfahrzeugbatteriewechseltechnikervereinigung です。^[return]