導入と歴史

グラフとは組 (pair) を集めたものです ――整数の組、人の組、都市の組、星の組、国の組、科学論文の組、ウェブページの組、ゲームの配置の組、再帰的な小問題の組、さらにグラフの組だって考えます。グラフを図示するときに一番よく使われる方法と対応して、組にされるオブジェクトは頂点 (vertex) あるいはノード (node) と呼ばれ、組そのものは辺 (edge) あるいは弧 (arc) と呼ばれます。しかしもちろん、オブジェクトと組はどんなものでも構いません。

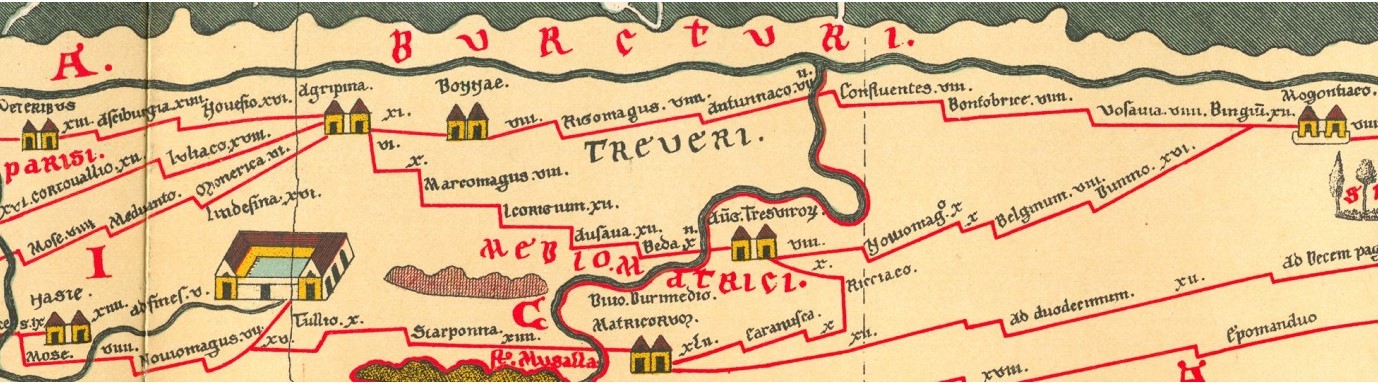
人類が初めてグラフを使った例の一つは、道路ネットワークを表した地図です。ローマ帝国時代、ローマの技師たちはヨーロッパ、西アジア、中央アジア、北アフリカを横断する 400,000km 以上に及ぶ道路ネットワークを構築しました。この道路を利用する旅人はイティネラリア (itineraria) と呼ばれる、道路沿いにある目印や道路の長さを図示した巻物を携帯していました。ポイティンガー図 (Tabula Peutingeriana) はローマのクルスス・プブリクス (Cursus publicus、ローマ帝国の駅伝制度) を図示した十三世紀の巻物ですが、これのもとになったのは一世紀のアウグストゥス・カエサルの治世中に作成されたイティネラリア・ピクタム (itinerarium pictum) を五世紀に改訂したものであると広く信じられています。ポイティンガー図は地理的に正しい地図ではありません ――歴史家の間にはそもそもこれを地図と呼んでもいいのかという議論さえあります！―― が、道路ネットワークを抽象的に表現しており、その意味では現代の地下鉄の地図と同じと言えます。

ポイティンガー図では道路沿いの都市が道路の垂直に折れる部分で表され、都市の名前や都市の間の道路の長さも地図に示されます。そのためこの地図には五世紀のローマ帝国における任意の二都市間の最短経路を見つけるのに十分な情報が含まれています。

1872 年に Konrad Miller によって行われたポイティンガー図の復元の一部分を抜粋したもの。現代の Birten (Veteribus、左上) から Köln (Agripine) と Bonn (Bonnae) を通って Mainz (Mogontiaco、右上) に至るまでのローマ道路には、 Trier (Avg Tresvirorvm、中央) や Metz (Matricorvm、中央下) への分かれ道がある。 — 図 5.1

1872 年に Konrad Miller によって行われたポイティンガー図の復元の一部分を抜粋したもの。現代の Birten (Veteribus、左上) から Köln (Agripine) と Bonn (Bonnae) を通って Mainz (Mogontiaco、右上) に至るまでのローマ道路には、 Trier (Avg Tresvirorvm、中央) や Metz (Matricorvm、中央下) への分かれ道がある¹。

グラフ (の一種である木) の最も古い古典的な応用例の一つは、グラフで表された家系図です。結婚や相続あるいは皇帝の跡継ぎに関する法的な問題を解決するときには、複雑な家系 "木" が何世紀にも渡って使われてきました。後に初期のカトリック教会法に組み込まれることになるローマ法では、いとこよりも近い近親との結婚が禁止されます。つまりローマの computatio legalis では、男女の一番近い共通の祖先との距離の和が少なくとも 4 であることが結婚のために必要でした。九世紀になって教会は必要とされる距離とその計算方法を変更し、新しい computatio canonica は一番近い祖先との距離の最大値が少なくとも 7 であることを要求しました。1215 年には実際に計算を行うのが困難なこと (そして実際に行われていた慣習) に屈する形で、教会は結婚できる距離を 4 としました²。

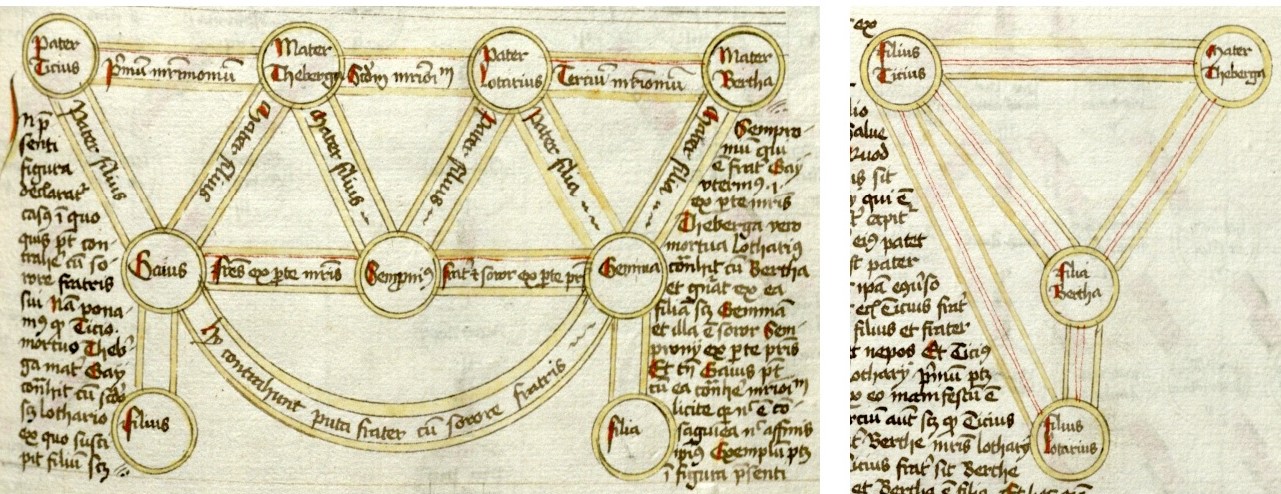
次の画像に示すのは特に複雑なケースです: 「Tirius と Theburga が結婚し、Tirius が死亡した後に Gaius という子が産まれた。その後 Theburga は Lothar と結婚し、子をもうけ、死亡した。さらに Lothar は Bertha と結婚し、 Gemma という娘をもうけた。 Gaius は合法的に Gemma の娘と結婚できるか？」

複雑な婚姻関係を示す二つの図。十四世紀に Johannes Andreae によって書かれた教会法に関する論文 <i>Super arboribus consanguinitatis et affinitatis</i> についての著者不明の十五世紀の論文より。 — 図 5.2

複雑な婚姻関係を示す二つの図。十四世紀に Johannes Andreae によって書かれた教会法に関する論文 *Super arboribus consanguinitatis et affinitatis* についての著者不明の十五世紀の論文より³。

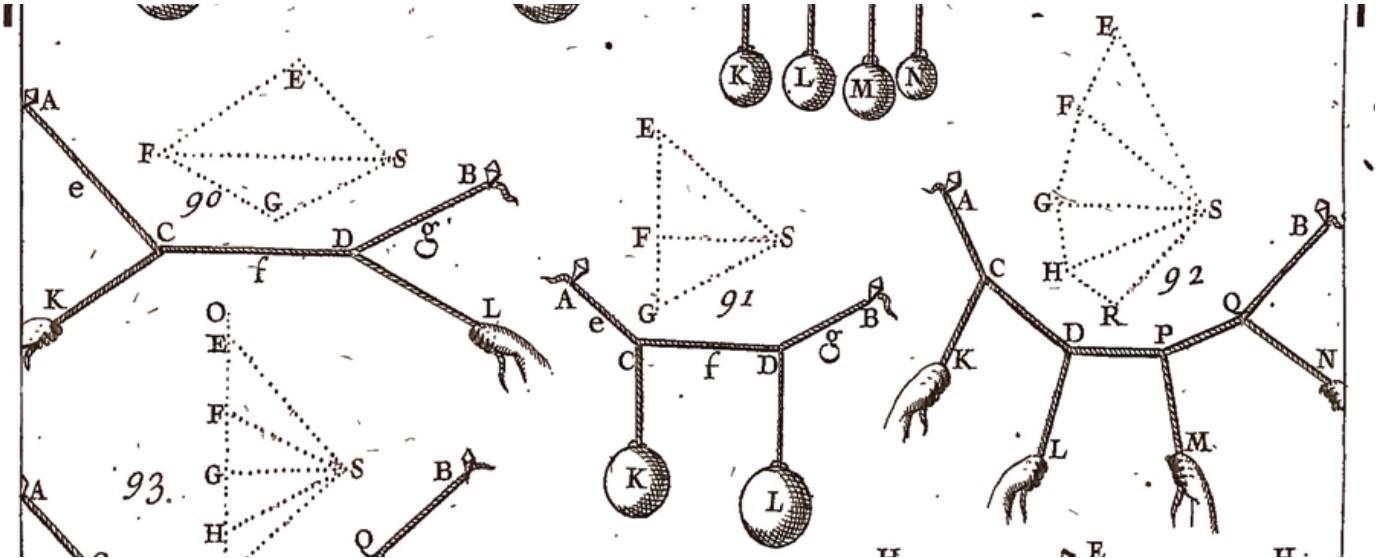
1680 年代の中頃、約一世紀前に出版された Simon Stevin (シモン・ステヴィン) による初期研究を発展させる形で、フランス人数学者 Pierre Varignon (ピエール・ヴァリニョン) は木の形をしたロープのネットワークに張力が働いたときの平衡位置を図を使って計算する方法を開発しました。Varignon が気付いたのは、ロープが平衡状態にあるとき、辺がロープ片と平行なグラフであって、辺の長さが張力と等しく、任意のロープ片の交わる点にグラフの閉路が対応するものが存在するということでした。Varignon の図式に関する研究は彼の死から二年後の 1725 年に完全な形で出版されました。このグラフは現在では reciprocal force diagram あるいは Maxwell-Cremona diagram という名前で知られています。James Clerk Maxwell (ジェームズ・クラーク・マクスウェル) と Luigi Cremona (ルイージ・クレモナ) は Carl Culmann (カール・クールマン) らと共に 1800 年代の終わりにかけてこの図式をもとにした広大な理論を構築しました。

reciprocal force diagram (破線)。 Varignon の死後に出版された <i>Nouvelle mécanique, ou statique, dont le projet fut donné en MDCLXXXVII</i> (『新しい力学および静力学、1687 年開始のプロジェクト』) より。 — 図 5.3

reciprocal force diagram (破線)。 Varignon の死後に出版された *Nouvelle mécanique, ou statique, dont le projet fut donné en MDCLXXXVII* (『新しい力学および静力学、1687 年開始のプロジェクト』) より⁴。

もちろんこれ以外にも身近なグラフの例はたくさんあります:

ボードゲーム: 古代までさかのぼります。
多面体の頂点と辺: 古代ギリシャの哲学者によって詳細に研究されましたが、さらに古い起源を持ちます。
星型模様の可視化: 東アジアで紀元前七世紀には行われていました。
ナイトツアー: 九世紀から十世紀にかけて al-Adli (アル=アドリ)、Rudrata (ルドラータ)、al-Suli (アル=スリ) らによって解明されました。
迷路: 現代的なものは Giovanni Fontana (ジョバンニ・フォンタナ) によって 1420 年ごろに作成されました。
三角測量: Gemma Frisius (ゲンマ・フリシウス) によって 1533 年に発明され、1615 年には Willebrord Snell (ヴィレブロルト・スネル) が地球の全周を求めるのに利用し、1799 年にはメートルを定義するのに使われました。
Leonhard Euler (レオンハルト・オイラー) によるケーニヒスベルクの橋パズルに対するよく知られた部分的な⁵解 (1735)
電報およびその他の通信ネットワーク: 最初に提案されたのは 1753 年、その後 1800 年代初頭に Francis Ronalds (フランシス・ロナルズ)、Pavel Schilling (パヴェル・シリング)、Carl Friedrich Gauss (カール・フリードリヒ・ガウス)、Wilhelm Weber (ヴィルヘルム・ヴェーバー) らによって実際に作成され、 1800 年代後半には世界中に配備されました。
電子回路: Georg Ohm (ゲオルク・オーム)、James Clerk Maxwell (ジェームズ・クラーク・マクスウェル)、Gustav Kirchhoff (グスタフ・キルヒホッフ) らによって 1800 年代初等に定式化されました。
分子構造の法則: 1857 年には August Kekulé (アウグスト・ケクレ) によって、1858 年には Archibald Couper (アーチボルド・クーパー) によってそれぞれ独立に発見されました。
ソーシャルネットワーク: 社会学者 Jacob Moreno (ヤコブ・モレノ) によって 1930 年代中ごろに初めて研究されました。
デジタル電子回路: Charles Sanders Pierce (チャールズ・サンダース・パース) によって 1886 年に提案され、Claude Shannon (クロード・シャノン) によって現代的な形になりました。

えぇ、どうしてもというなら言いますよ、現代のインターネットもグラフを使っています。

抽象的な数学的対象としての「グラフ (graph)」という言葉は 1878年に James Sylvester (ジェームス・シルベスター) によって初めて使われました。彼が graph という単語を使い始めたのは、Kekulé がとある代数的不変量を表現するために "chemicograph" という言葉を使っていることを同僚であった William Clifford (ウィリアム・クリフォード) から聞いたためであったと言います。また連結非巡回グラフを「木 (tree)」と始めて呼んだのは Arthur Cayley (アーサー・ケイリー) で、1853 年のことです。ただし抽象的な対象としての木は Gustav Kirchhoff (グスタフ・キルヒホッフ) と Karl von Staudt (カール・フォン・シュタウト) によってそれより 10 年前に使われていました。グラフ理論に関する André Sainte-Laguë (アンドレ・サン＝ラグ) による本の第零版は 1926 年に出版され、Dénes Kőnig (デネス・ケーニヒ) による本はそれから十年後です。

ソース: https://commons.wikimedia.org/wiki/File:Tabula_Peutingeriana_-_Miller.jpg (CC0)^[return]
十一世紀と十二世紀にかけて、結婚の制限は姻戚関係を通じて適用されるようになりました。最初は結婚による姻戚関係だけが考慮されましたが、後になって婚外性交渉や婚約、そして名づけ親関係さえも考慮されるようになりました。例えばある男とその姉妹の夫の姉妹の夫の姉妹との結婚は正式に禁止されていました。また男やもめとその息子の妻の親である未亡人との結婚も同じく禁止でした。1215 年の改定でこの姻戚関係に関する制限は大きく緩和されましたが、削除はされませんでした。教会が姻戚関係 ex copula illicita という概念を捨て去ったのはようやく 1917 年のことです。^[return]
ソース: https://archive.org/details/A077240124/page/n261 (Biblioteca de la Universidad de Sevilla, パブリックドメイン)^[return]
Euler は議論の最後のステップ ――全ての頂点の次数が偶数であるグラフのオイラー路を実際に求めること―― を明らかだとして省略しています。またグラフがオイラー路を持つにはグラフが連結である必要があることにも Euler は気付いていませんでした。グラフがオイラー路を持つこととグラフが連結で全ての頂点が偶数であることが同値である証明を最初にきちんと示したのは Carl Hierholzer であり、1873 年のことです。^[return]