Hanoi の塔

Hanoi (ハノイ) の塔は 1883 年¹にフランス人教師で娯楽数学者でもあった Éduoard Lucas (エドゥアール・リュカ) によって²最初に発表されました ――実際に遊べるパズルとして！ その次の年、Henri de Parville (アンリ・ド・パルヴィル) はこのパズルを次のストーリーと共に紹介しています³:

Benares (ベナレス) にある大寺院⁴...世界の中心にあるドームには、三つのダイアモンドの棒が刺さった真鍮のプレートがある。棒の高さは 1 キュービット (約 50 cm) であり、太さはハチの体ほどである。この世を創生するときに、神は 64 個の金の円盤を棒の一つに通して置いた。そのとき神は一番大きな円盤が真鍮のプレートと接するように、そして上に行けば行くほど円盤が小さくなるようにした。これが Bramah (ブラマー) の塔である。司祭たちは昼夜とめどなく円盤をひとつの棒から他の棒に移動させる。円盤を移動させるとき、司祭たちは絶対の Bramah の法に従う。つまり、円盤は必ずひとつずつ移動させなければならず、ある円盤の下にそれよりも小さい円盤があるようにすることはできない。 64 個の円盤を神が創生のときに使った棒から別の棒に全て移動させることができたならば、塔、寺院、そして Brahmin (バラモン) は塵となり、雷鳴と共に世界は消えてしまうという。

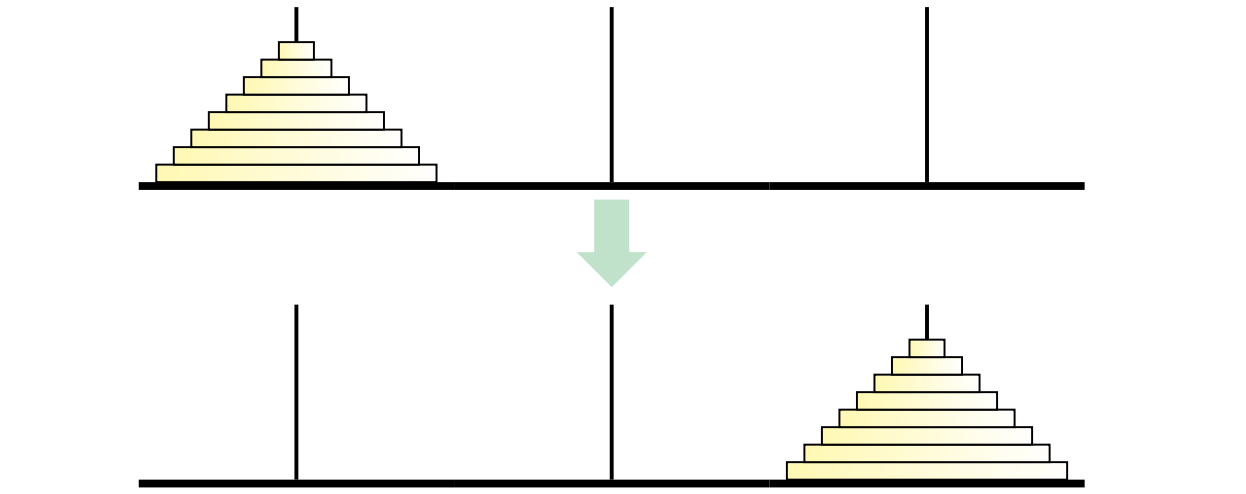
私たちは善き計算機科学者として、この物語に出現する定数 64 を変数 \(n\) で置き換えます (当然です)。それから物理的なパズルは通常ダイアモンドと金ではなく木でできているので、円盤を入れる場所のことを棒ではなく杭と呼ぶことにします。三番目の杭を一時的な置き場所として使いながら、円盤を自身よりも小さい円盤の上に置くことなく、\(n\) 個の円盤を二番目の杭に移動させるにはどうすればよいでしょうか？

N. Claus de Siam もパズルに付いてくるパンフレットで語っていることですが、このパズルを解く鍵は再帰的に考えることにあります。パズル全体を一度に解こうと考えるのをやめて、まず一番大きい円盤を動かすことに集中しましょう。最初の状態では一番大きい円盤の上には他の全ての円盤が載っているので、この円盤を動かすことはできません。そのため最初に \(n - 1\) 個のディスクを一時的な置き場所の杭に移動させる必要があります。それから一番大きな円盤を目標の杭に移動させ、最後に \(n-1\) 個の円盤をその上に移動させれば良いことになります。

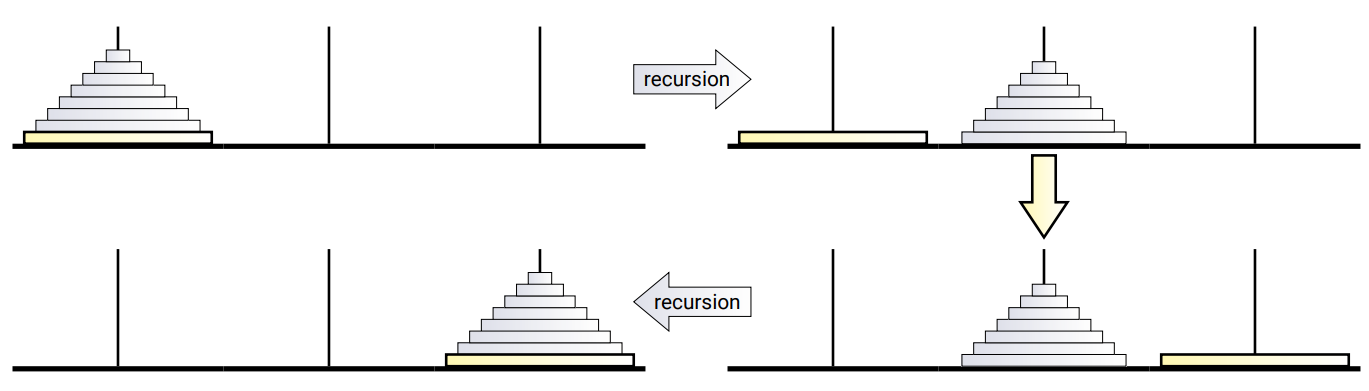
さて、次に行うべきは――

もうこれですべきことは終わっています！ 円盤が \(n\) 個のHanoi の塔の問題を円盤が \(n-1\) 個のHanoi の塔の問題を二回使って解くことができたので、あとは再帰の妖精 (Lucas の比喩を借りるなら "寺院の新人僧侶") に任せることができます。私たちの 仕事はこれで終わりです。信用できない僧侶が雇われるはずはありませんから、新人僧侶にあれこれ言うのはやめましょう。

この帰着にはとても重要で気付かれにくい仮定があります。一番大きい円盤の存在です。この再帰的なアルゴリズムは円盤の数が正のときだけ上手く動き、\(n = 0\) のときには処理を行うことができません。幸い Benares の僧侶は敬虔な仏教徒なので、全く苦労せずにゼロ個の円盤をある杭から別の杭に移動させることができます: 何もしなければいいのです。

パズルを解く中で他の小さい円盤がどう動くのか、あるいはもっと一般的に再帰的な手続きが展開されたときに何が起こるのかを知りたくなるかもしれません。それでも、どうか踏みとどまってください。ほとんどの再帰的なアルゴリズムにおいて、再帰を展開することは必要でもありませんし、理解に役立つわけでもありません。すべきことは、問題のインスタンスをより単純なインスタンスに帰着させる、それが不可能ならば直接解く、それだけです。Hanoi の塔のアルゴリズムは \(n=0\) のとき明らかに正しく、そして \(n \geq 1\) のときには再帰の妖精が上にある \(n - 1\) 個の円盤動かしてくれるので (きちんと言うと、帰納法の仮定よりこの再帰的なアルゴリズムは \(n-1\) 個の円盤を正しく移動させるので)、このアルゴリズムは任意の \(n\) に対して正しいことが分かります。

Hanoi の塔のアルゴリズムは次のように表されます。このアルゴリズムは \(n\) 個の円盤を元々あった杭 \(\mathit{src}\) から目的地の杭 \(\mathit{dst}\) へ、三番目の杭 \(\mathit{tmp}\) を一時的な置き場所として使いながら移動させます。このアルゴリズムは \(n=0\) のときにも正しいことに注意してください。

\(n\) 個の円盤を移動させるのにかかる時間 ――このアルゴリズムの実行時間―― を \(T(n)\) とします。\(n = 0\) のときは何もしないので、 \(T(0) = 0\) です。そして一般の \(n \geq 1\) に対するアルゴリズムから、\(T(n) = 2T(n-1) + 1\) が分かります。いくつかの \(n\) について実際に値を計算すると、 \(\pmb{T(n) = 2^{n} - 1}\) であることが予想でき、単純な帰納法によってこの答えの正しさが証明できます。

64 個の円盤を移動するのにかかる移動の回数を実際に計算すると、\(2^{64}-1 =\) \(18,\allowbreak446,\allowbreak446\allowbreak744,\allowbreak073,\allowbreak709,\allowbreak551,\allowbreak615\) 回となります。一秒に一回というとても速いスピードで円盤を動かしたとしても、 Brahmin が塵となり、雷鳴と共に世界が消えるまでには、Benares の僧侶は 5850億年 ("plus de cinq milliards de siècles") の間働き続けなくてはいけません。

1. Lucas は後に Hanoi の塔を発明したのは 1876 年であったと述べています。^[return]

2. Lucas は Hanoi の塔を発表するときに N. Claus de Siam (シャムのクロース) という名前を使いました。この名前は "Lucas d'Amiens" (アミアンのリュカ) のアナグラムです。^[return]

3. この英語訳は W. W. Rouse Ball の 1892 年の著作 Mathematical Recreations and Essays. より。^[return]

4. "Benares にある大寺院" とはほぼ間違いなくインドのウッタル・プラデーシュ州ヴァーラーナシーにあるカーシー・ヴィシュヴァナート寺院のことです。この寺院は N. Claus という空想上の人物が住んでいるというベトナムのハノイからは 2400 km 西北西にあります。偶然にも、フランス軍がハノイに侵攻したのは 1883 年であり、Lucas が Hanoi の塔パズルを発表したのと同じ年です。この侵攻はフランス領インドシナの首都の成立につながりました。^[return]