トポロジカルソート
有向グラフ \(G\) のトポロジカル順序とは、頂点の間の全順序 \(\prec\) であって全ての辺 \(u \rightarrow v\) に対して \(u \prec v\) が成り立つものを言います。くだけて言うと、トポロジカル順序とは全ての辺が右から左に行くように頂点を一列に並べたものです。\(G\) が有向閉路を持っている場合にはトポロジカル順序が存在しないのは定義から明らかです ――閉路に含まれる頂点のうち一番右にある頂点からは左に向かう辺が出てしまいます!
有向グラフ \(G\) の任意の帰りがけ順序を考えます。前述の解析より、\(\mathit{u.post} < \mathit{v.post}\) を満たす任意の辺 \(u \rightarrow v\) に対して \(G\) には \(v\) から \(u\) への有向路が含まれます。したがってもし \(G\) が非巡回ならば、全ての辺 \(u \rightarrow v\) に対して \(\mathit{u.post} > \mathit{v.post}\) です。ここから任意の有向非巡回グラフ \(G\) がトポロジカル順序を持つことが言えます。具体的には、\(G\) の任意の帰りがけ順序を逆にしたものが \(G\) のトポロジカル順序です。
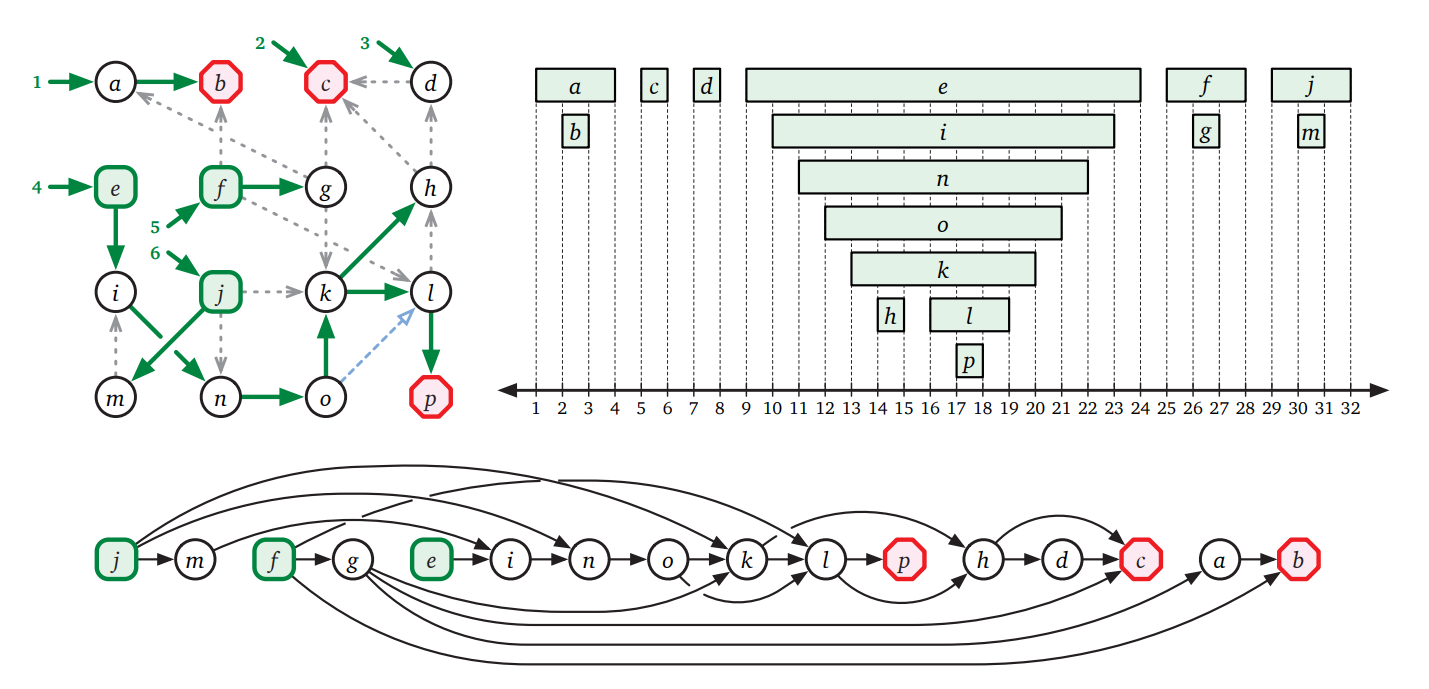
トポロジカル順序を別のデータ構造に書き出す必要があるなら、探索の途中で頂点をそのまま配列に書くことで \(O(V+E)\) 時間で行えます:
procedure \(\texttt{TopologicalSort}\)(\(G\))
for 頂点 \(v\) do
\(\mathit{v.status} \leftarrow \textsc{New}\)
\(\color{red}{\mathit{clock} \leftarrow V}\)
for 頂点 \(v\) do
if \(\mathit{v.status} = \textsc{New}\) then
\({\color{red}{\mathit{clock}}} \leftarrow\,\)\(\texttt{TopSortDFS}\)(\(v, \color{red}{\mathit{clock}}\))
return \(\color{red}{S[1..V]}\)
procedure \(\texttt{TopSortDFS}\)(\(v, \color{red}{\mathit{clock}}\))
\(\mathit{v.status} \leftarrow \textsc{Active}\)
for \(v \rightarrow w\) の形をした辺 do
if \(\mathit{w.status} = \textsc{New}\) then
\({\color{red}{\mathit{clock}}} \leftarrow\,\)\(\texttt{TopSortDFS}\)(\(w, \color{red}{\mathit{clock}}\))
\(\mathit{v.status} \leftarrow \textsc{Finished}\)
\({\color{red}{S[\mathit{clock}]} \leftarrow v}\)
\({\color{red}{\mathit{clock}} \leftarrow \mathit{clock} - 1}\)
return \(\color{red}{\mathit{clock}}\)
陰的なトポロジカルソート
しかしトポロジカル順序を別のデータ構造に格納するというのは多くの場合やりすぎです。トポロジカルソートの応用では頂点をトポロジカル順序に並べたリストが得たいのではなくて、トポロジカル順序 (あるいはその逆順) に沿って頂点ごとに何らかの計算を行いたい状況がほとんどであり、このような応用では、グラフのトポロジカル順序を記録する必要はありません!
有向非巡回グラフの頂点をトポロジカル順序の逆順で処理したいならば、頂点を再帰的深さ優先探索の最後で処理するようにすればそれで済みます。結局、トポロジカル順序とは帰りがけ順序の逆順なのですから!
procedure \(\texttt{PostProcess}\)(\(G\))
for 頂点 \(v\) do
\(\mathit{v.status} \leftarrow \textsc{New}\)
for 頂点 \(v\) do
if \(\mathit{v.status} = \textsc{New}\) then
\(\texttt{PostProcessDFS}\)(\(v\))
procedure \(\texttt{PostProcessDFS}\)(\(v\))
\(\mathit{v.status} \leftarrow \textsc{Active}\)
for \(v \rightarrow w\) の形をした辺 do
if \(\mathit{w.status} = \textsc{New}\) then
\(\texttt{PostProcessDFS}\)(\(w\))
else if \(\mathit{w.status} = \textsc{Active}\) then
エラーを出す
\(\mathit{v.status} \leftarrow \textsc{Finished}\)
\(\texttt{Process}\)(\(v\))
もし入力されるグラフが非巡回であることが事前に分かっているなら、頂点の状態を保存する代わりに印をつけるようしてこのアルゴリズムをさらに簡略化できます:
procedure \(\texttt{PostProcessDag}\)(\(G\))
for 頂点 \(v\) do
\(v\) の印を消す
for 頂点 \(v\) do
if \(v\) に印が付いていない then
\(\texttt{PostProcessDagDFS}\)(\(v\))
procedure \(\texttt{PostProcessDagDFS}\)(\(v\))
\(v\) に印をつける
for \(v \rightarrow w\) の形をした辺 do
if \(w\) に印が付いていない then
\(\texttt{PostProcessDFS}\)(\(w\))
\(\texttt{Process}\)(\(v\))
これは一般的な深さ優先探索と全く同じで、 \(\textsc{PostVisit}\) が \(\textsc{Process}\) に変わっているだけです!
有向非巡回グラフに対する帰りがけ順の処理はとてもよく使われるので、私はこの処理を次のように省略して書くことがあります:
procedure \(\texttt{PostProcessDAG}\)(\(G\))
for 帰りがけ順の頂点 \(v\) do
\(\textsc{Process}(v)\)
例えば先述の陽的なトポロジカルソートは次のように書けます:
procedure \(\texttt{TopologicalSort}\)(\(G\))
\(\mathit{clock} \leftarrow V\)
for 帰りがけ順の頂点 \(v\) do
\(S[\mathit{clock}] \leftarrow v\)
\(\mathit{clock} \leftarrow \mathit{clock} - 1\)
return \(S[1..V]\)
DAG をトポロジカル順序通りに処理したい場合には、頂点をトポロジカル順序に配列に保存し、その配列に対して単純な for ループを回すことで行えます。順序を配列に書き出すことができない場合には、DAG \(G\) の逆 (reversal) と呼ばれるグラフに対して深さ優先探索を行うことでも同じ処理を行えます。有向グラフ \(G\) の逆とは \(G\) の全ての辺 \(u \rightarrow w\) を \(u \leftarrow w\) に取り換えることで得られるグラフであり、\(\mathit{rev}(G)\) と表されます。有向グラフ \(G\) に含まれる閉路は \(\mathit{rev}(G)\) でも閉路を作るので、DAG の逆は DAG です。\(G\) におけるシンクは \(\mathit{rev}(G)\) におけるソースとなります (逆も成り立ちます)。また \(\mathit{rev}(G)\) におけるトポロジカル順序が \(G\) のトポロジカル順序の逆順であることは帰納法によって示せます1。標準的な隣接リストで表された任意の有向グラフの逆は \(O(V+E)\) で計算できます: 詳細は簡単な練習問題とします。
-
\(G\) の逆の帰りがけ順序が \(G\) の帰りがけ順序の逆順であるとは限りませんが、\(G\) のトポロジカル順序であることは言えます。[return]