最大フロー最小カット定理

意外なことに、任意のフローネットワークは \(|f| = \| S, T \|\) を満たす \((s,t)\)-フロー \(f\) と \((s,t)\)-カット \((S, T)\) を必ず持ちます。これが有名な最大フロー最小カット定理 (Maxflow-Mincut Theorem) です。この定理は Lester Ford (レスター・フォード、最短路アルゴリズムで知られる) と Delbert Fulkerson (デルバート・ファルカーソン) によって 1954 年に初めて証明され、1956 年には Peter Elias (ピーター・イライアス) と Amiel Feinstein (アミエイ・ファインスタイン) と Claude Shannon (クロード・シャノン、迷路を解くロボットと情報理論で知られる) によって独立に証明されています。

これから示すのは Ford と Fulkerson が行った証明です。\(G\) を任意のグラフ、\(s, t\) を \(G\) の適当な頂点、\(c:E \rightarrow \mathbb{R}_{\geq 0}\) を容量関数とします。証明はグラフが既約 (reduced) であること、つまり \(u\) と \(v\) の間には最大でも一つの辺しかないことを仮定すると簡単になります。既約という条件を言い換えると、任意の \(u \rightarrow v\) について \(c(u \rightarrow v) = 0\) または \(c( v \rightarrow u) = 0\) の少なくとも一方が必ず成り立つということです。この仮定は任意のグラフに対して簡単に強制できます: \(G\) の全ての辺に対して新しい頂点 \(x\) を追加し、 \(u \rightarrow v\) という辺を \(u \rightarrow x \rightarrow v\) という路に入れ替え、\(c(u \rightarrow x) =\) \(c (x \rightarrow v) = \) \(c(u \rightarrow v)\) と定義すると、改変されたグラフは元のグラフと同じ最大フローの値と最小カットの容量を持つ既約なグラフとなるためです。

\(G\) における任意の実現可能な \((s,t)\)-フローを \(f\) とし、\(f\) に対応する新しい容量関数 \(c_{f} : V \times V \rightarrow \mathbb{R}\) を次のように定義します。この容量関数を残余容量 (residual capacity) と呼びます: \[ c_{f} (u \rightarrow v) = \begin{cases} c(u \rightarrow v) - f (u \rightarrow v) & \text{if } u \rightarrow v \in E \\ f(v \rightarrow u) & \text{if } v \rightarrow u \in E \\ 0 & \text{それ以外} \end{cases} \] 直感的に言えば、ある辺の残余容量は現在その辺に流れている値に追加して流すことのできるフローの量を表します。\(f \geq 0\) かつ \(f \leq c\) なので残余容量の値は非負です。

元のグラフ \(G\) に辺 \(u \rightarrow v\) が存在しなかったとしても \(c_{f}(u \rightarrow v) > 0\) となることがあり得ます。そのため \(E_{f}\) を残余容量が正である辺の集合とすると、\(G_{f} = (V, E_{f})\) は (\(G\) と異なるグラフである)残余グラフ (residual graph) を定義します。ほとんどの場合において、残余グラフは既約ではありません。具体的には \(0 < f ( u \rightarrow v) < c(u \rightarrow v) \) が成り立つとき、残余グラフ \(G_{f}\) には辺 \(u \rightarrow v\) と辺 \(v \rightarrow u\) の両方が含まれます。

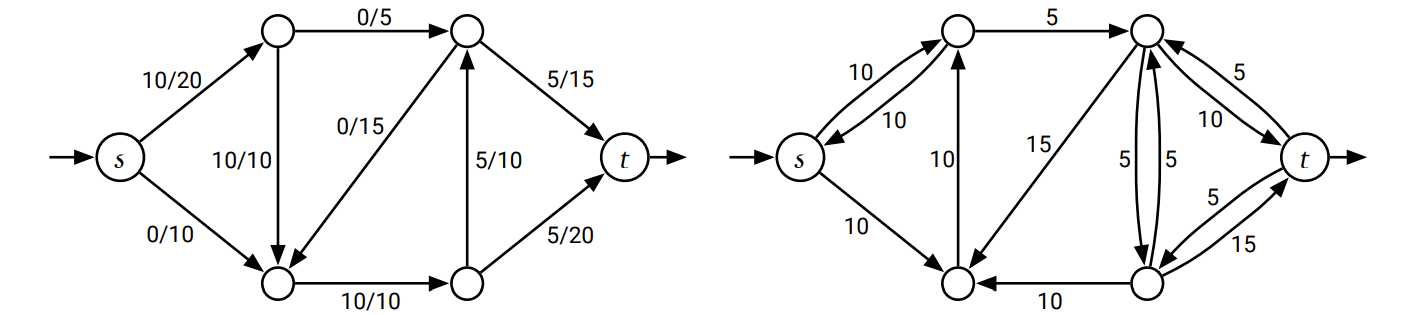
ここで考えるべきケースが二つあります。一つは残余グラフに \(G_{f}\) にソース頂点 \(s\) からシンク頂点 \(t\) までの有向路が存在する場合で、もう一つはそのような有向路が存在しない場合です。

まず残余グラフ \(G_{f}\) に \(s\) から \(t\) への有向路 \(P\) が存在するとします。このような路 \(P\) を増加路 (augumenting path) と呼びます。\(P\) に流せる最大のフローを \(\displaystyle F = \min_{u \rightarrow v \in P} c_{f} (u \rightarrow v)\) とし、(元のグラフにおける) 新しいフロー \(f^{\prime}: E \rightarrow \mathbb{R}\) を次のように定義します: \[ f^{\prime}(u \rightarrow v) = \begin{cases} f(u \rightarrow v) + F & \text{if } u \rightarrow v \in P \\ f(u \rightarrow v) - F & \text{if } v \rightarrow u \in P \\ f(u \rightarrow v) & \text{それ以外} \end{cases} \]

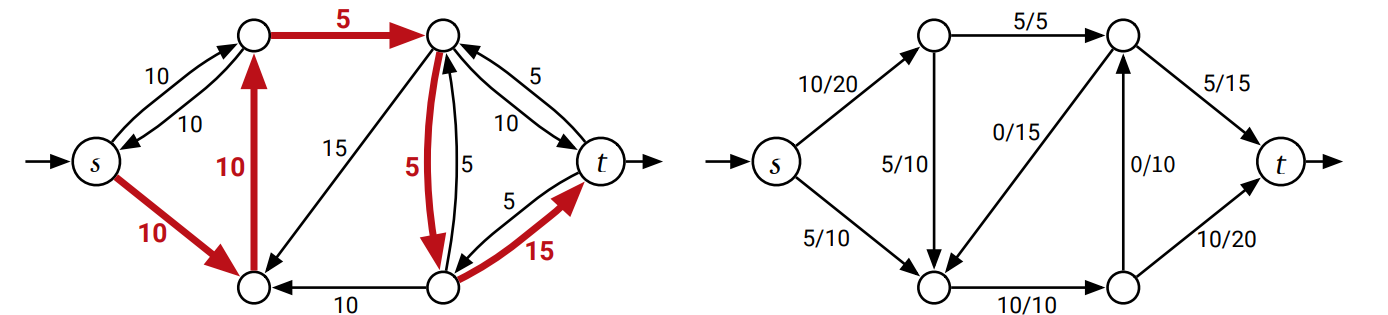
この新しいフロー \(f^{\prime}\) が元の容量 \(c\) に対して実現可能であること、つまり全ての辺に対して \(f^{\prime} \geq 0\) かつ \(f^{\prime} \leq c\) であることをこれから示します。元のグラフ \(G\) における辺 \(u \rightarrow v\) に対する三つのケースを考えます:

• \(P\) が \(u \rightarrow v\) を含むならば、\(f\) が実現可能なことより \[ f^{\prime} (u \rightarrow v) = f(u \rightarrow v) + F > f(u \rightarrow v) \geq 0 \] であり、また \[ \begin{aligned} f^{\prime} (u \rightarrow v) & = f(u \rightarrow v) + F && [f^{\prime} \text{ の定義}] \\ & \leq f(u \rightarrow v) + c_{f}(u \rightarrow v) && [F \text{ の定義}] \\ & = f(u \rightarrow v) + c(u \rightarrow v) - f(u \rightarrow v) && [c_{f} \text{ の定義}] \\ & = c(u \rightarrow v) && [\text{やったぜ}] \end{aligned} \] も成り立つ。

• \(P\) が \(u \rightarrow v\) の逆 \(v \rightarrow u\) を含むならば、ここでも \(f\) が実現可能なことから \[ f^{\prime} (u \rightarrow v) = f(u \rightarrow v) - F < f(u \rightarrow v) \leq c(u \rightarrow v) \] であり、また \[ \begin{aligned} f^{\prime}(u \rightarrow v) & = f(u \rightarrow v) - F && [f^{\prime} \text{ の定義}] \\ & \geq f(u \rightarrow v) - c_{f}(v \rightarrow u) && [F \text{ の定義}] \\ & = f(u \rightarrow v) - f(u \rightarrow v) && [c_{f} \text{ の定義}] \\ & = 0 && [\text{やったぜ}] \end{aligned} \] も成り立つ。

• 最後に \(u \rightarrow v\) も \(v \rightarrow u\) も増加路に含まれないなら \(f^{\prime}(u \rightarrow v) = f(u \rightarrow v)\) だから、 \(f\) が実現可能なことより \(0 \leq f^{\prime}(u \rightarrow v) \leq c(u \rightarrow v)\) が成り立つ。

よって \(f^{\prime}\) は実現可能です。

最後に、増加路で \(s\) から離れる辺は最初の辺だけなので \(|f^{\prime}| = |f| + F > |f|\) であり、したがって \(f^{\prime}\) は \(f\) よりも大きな値を持つ実現可能なフローです。以上より、残余グラフ \(G_{f}\) に \(s\) から \(t\) への路が存在するならば \(f\) は最大フローではないと言えます。

一方で残余グラフ \(G_{f}\) に \(s\) から \(t\) への有向路が含まれないとします。このとき \(G_{f}\) で \(s\) から到達可能な頂点の集合を \(S\) とし、さらに \(T = V \backslash S\) と定めると、分割 \((S, T)\) は明らかに \((s,t)\)-カットとなります。さらに任意の \(u \in S\) と \(v \in T\) について \(c_{f}(u \rightarrow v) = 0\) なことから \[ \begin{cases} c(u \rightarrow v) - f (u \rightarrow v) = 0 & \text{if } u \rightarrow v \in E \\ f(v \rightarrow u) = 0 & \text{if } v \rightarrow u \in E \end{cases} \] が成り立ちます。これを言い換えると、考えているフロー \(f\) は \(S\) から \(T\) へ向かう辺を全て飽和させ、\(T\) から \(S\) に向かう辺を全て避けるということです。よって 命題 10.1 より \(|f| = \|S,T\|\) であり、 \(f\) が最大フローで \((S, T)\) が最小カットであることが分かります。

証明はこれで完了です！ \(\Box\)