グラフの表現と例

グラフを可視化する最も簡単な方法は描くことです。描いたグラフのことを、グラフの描画 (drawing) と呼びます。グラフの描画は各頂点を平面上の (普通小さい円などで表される) 点に、各辺を頂点間の直線 (または曲線) に対応させます。どの辺も交わらないようにグラフを描画できるとき、グラフは平面 (planar) であると言い、そのような描画を埋め込み (embedding) と呼びます¹。同じグラフでも描画はいくつもあり得るので、特定の描画とグラフを混同しないようにしてください。特に、平面グラフにも平面的でない描画があり得ます！

しかし、グラフを上手く表現できるのは描画だけというわけではありません。例えば幾何学的なオブジェクトを使えば交差グラフ (intersection graph) が定義できます。交差グラフの頂点はその幾何学的なオブジェクトであり、その間に辺があるのはオブジェクト同士が交差するときだけです。特定のグラフが交差グラフとして表せるかどうかは頂点としてどんなオブジェクトを考えているかによって変化し、異なる幾何学的オブジェクト (線分、長方形、円など) は異なるグラフのクラスを定義します。特に有用な交差グラフは頂点が数直線上の区間に対応する区間グラフ (interval graph) であり、区間グラフの辺は二つの区間が重なるときに限って存在します。

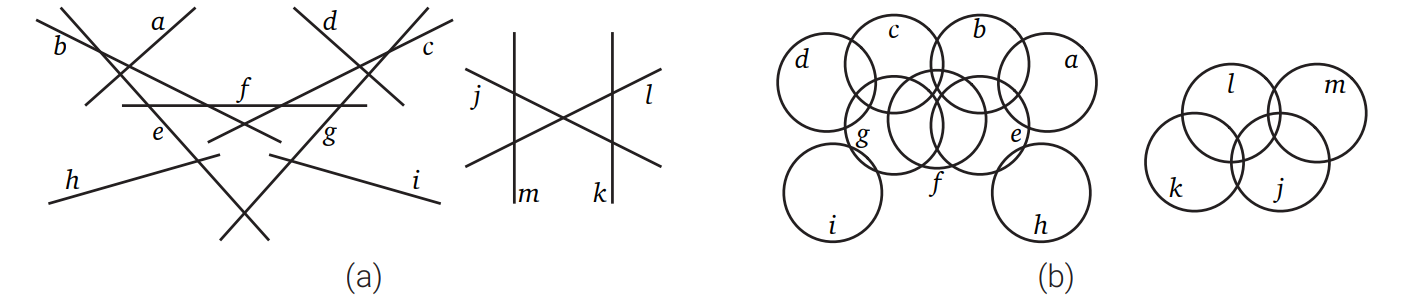
描画以外のグラフの表現のもう一つの良い例は、再帰的な問題に対する依存グラフ (dependency graph) です。依存グラフは有向非巡回グラフであり、頂点は特定の入力に対してアルゴリズムを実行したときに計算される再帰的な小問題を表します。二つの頂点の間に辺があるのは、頭の問題を実行するときに尾の問題が実行されるときだけです。例えばフィボナッチ数列の再帰方程式 \[ F_{n} = \begin{cases} 0 & \text{if } n = 0 \\ 1 & \text{if } n = 1 \\ F_{n-1} + F_{n-2} & \text{それ以外} \end{cases} \] に対する依存グラフは頂点が \(0, 1, 2, \ldots ,n\) であり、2 から \(n\) についての \(i\) について \((i-1) \rightarrow i\) と \((i-2) \rightarrow i\) という辺が存在します:

より複雑な依存グラフを持つ再帰方程式の例としては、三章で扱った編集距離問題に対する再帰方程式があります: \[ \mathit{Edit}(i, j) = \begin{cases} i & \text{if } j = 0 \\ j & \text{if } i = 0 \\ \min \left\lbrace \begin{array}{c} \mathit{Edit}(i - 1, j) + 1 \\ \mathit{Edit}(i, j - 1) + 1 \\ \mathit{Edit}(i - 1, j - 1) + [A[i] \neq B[j]] \end{array} \right\rbrace & \text{それ以外} \end{cases} \]

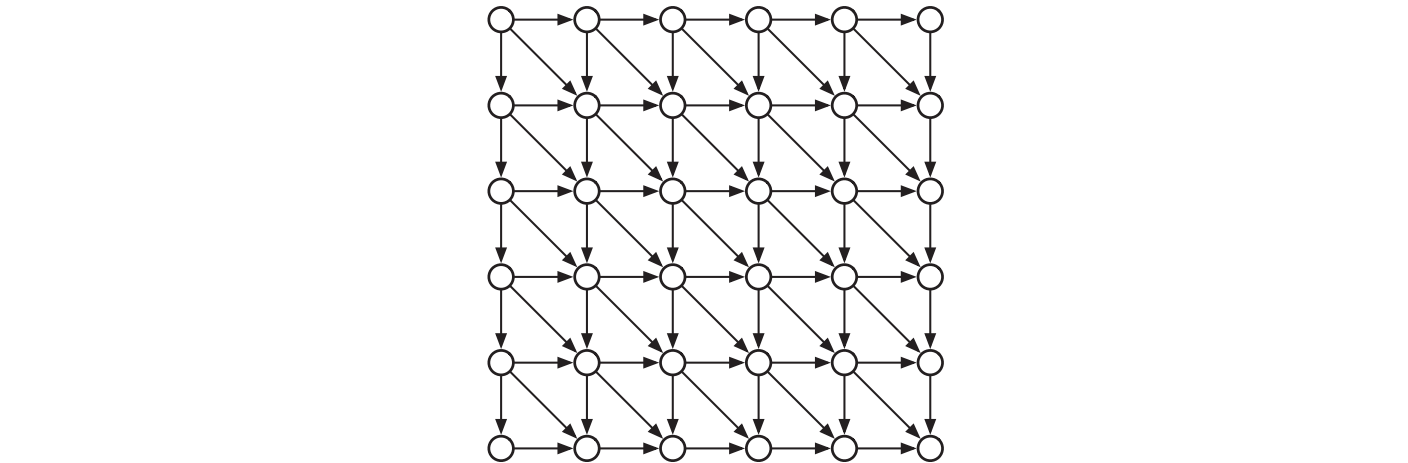
この再帰方程式に対する依存グラフは \(m \times n\) の格子であり、頂点 \((i, j)\) が垂直な辺 \((i-1, j) \rightarrow (i, j)\) と平行な辺 \((i, j - 1) \rightarrow (i, j)\) と対角方向の辺 \((i - 1, j - 1) \rightarrow (i, j)\) で結ばれています。動的計画法が効率良く動作するのは依存グラフが十分小さい場合であり、動的計画法の正しい評価順序では全ての小問題がその前者よりも後に解かれることが保証されます。

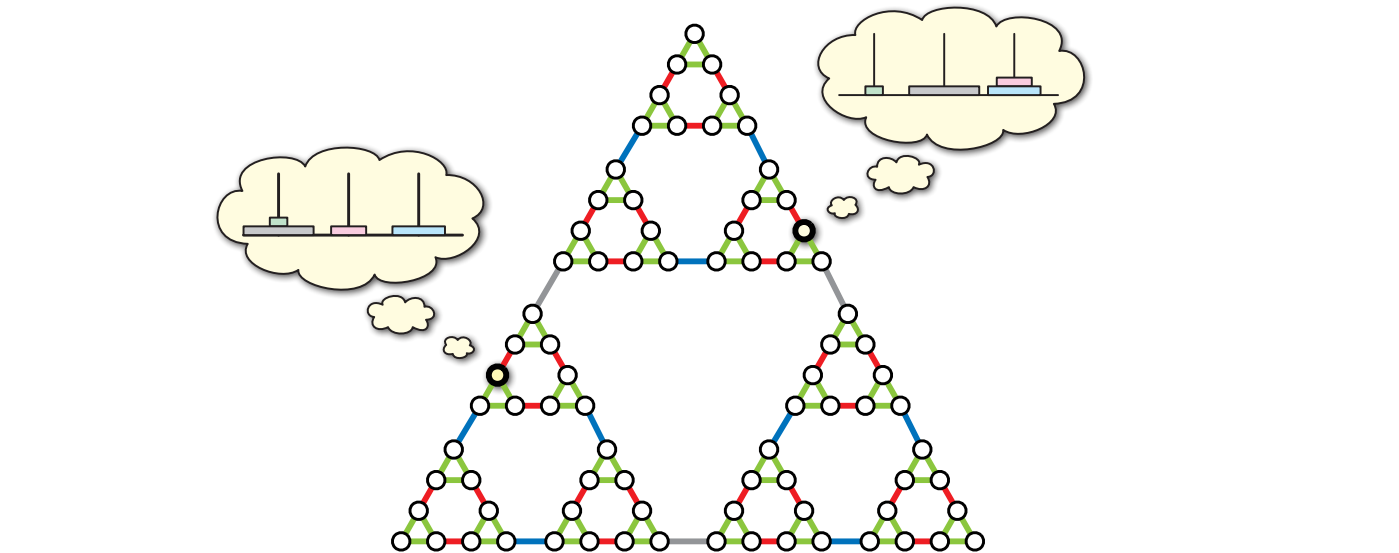
もう一つの面白い例は、ゲーム、パズル、あるいは tic-tac-toe やチェッカー、ルービックキューブなどの装置に対して定義される構成グラフ (configuration graph) です。頂点がパズルの合法な構成を表し、ある構成から別の構成に一つの手で移れる場合に限って対応する頂点の間に辺があります (明らかに、グラフの正確な定義はゲームの合法手が何であるかに依存します)。単純な装置であっても構成グラフが非常に複雑になることがあり、考えている構成グラフの一部に対してしかアクセスできないのが普通です。

構成グラフは二章で考えたゲーム木とよく似ていますが、重要な違いがあります。それは、ゲーム木には同じ状態が何度も現れるのに対して、構成グラフには同じ状態がちょうど一つだけ含まれる点です。つまり、構成グラフはメモ化されたゲーム木です！

形式言語理論で使われる有限状態オートマトン (finite-state automata) もラベル付きの有向グラフとしてモデル化できます。決定性有限状態オートマトンの形式的な定義は 5-タプル \(M = (\Sigma, Q, s, A, \delta)\) を使うものであり、ここで \(\Sigma\) はアルファベットと呼ばれる有限集合、 \(Q\) は状態の有限集合、\(s \in Q\) は開始状態、\(A \subseteq Q\) は受理状態、 \(\delta: Q \times \Sigma \rightarrow Q\) は遷移関数を表します。しかしこの定義を使わずに \(M\) を有向グラフ \(G_{M}\) として定義し、\(G_{M}\) の頂点が状態 \(Q\) で、全ての \(q \in Q\) と \(a \in \Sigma\) に対して \(q \rightarrow \delta(q, a)\) という辺が存在するとした方が考えやすいことが多いです。 \(M\) が受理する言語 \(L(M)\) に関する基本的な問題はグラフ \(G_{M}\) に対する問題に変換できます。例えば、 \(L(M) = \varnothing\) は開始状態/頂点 \(s\) から到達可能な受理状態/頂点が存在しないことと同値です。

最後に、あるグラフがもっと大きなグラフを暗黙のうちに表現することがあります。分かりやすい例は NFA を DFA に変換するときに使う部分集合の構築です。具体的には、与えられた有向グラフ \(G=(V, E)\) から新しい有向グラフ \(G^{\prime} = (2^{V}, E^{\prime})\) を作る操作です。ここで頂点 \(2^{V}\) は \(V\) の全ての部分集合であり、辺 \(E^{\prime}\) は次の式で定義されます: \[ E^{\prime} := \lbrace A \rightarrow B\ |\ \text{ある } u \in A \text{ と } v \in B \text{ があって } u \rightarrow v \in E \rbrace \] この定義を機械的に翻訳すれば \(G\) から \(G^{\prime}\) を構築するアルゴリズムが得られますが、この構築は必要ではありません。なぜなら \(\pmb{G}\) は既に \(\pmb{G^{\prime}}\) の陰的な表現だからです。

ここまでに説明してきた例/表現を正式な定義と混同しないように注意してください。グラフとは集合の組 \((V, E)\) であり、\(V\) は任意の集合、\(E\) は \(V\) の要素の (順序の有る、または無い) 組の集合です。一言で言えば: グラフは物の組の集合です。

1. 紛らわしいことに、埋め込み (embedding) という言葉が辺が交わる埋め込みに対して、描画と同じ意味で使われることがあります。あなたはこのようなことをしないでください。^[return]