さらなる進展

最大フローアルゴリズムの物語はこれで終わりでは決してありません。何十年にも渡る高速なアルゴリズムの研究の成果を次の表にまとめます¹。ここにあるアルゴリズムは全て反復によって最大フローを計算するものであり、ほとんどのアルゴリズムには二つのバージョンがあります: 一つは各反復で総当たりを使う単純なバージョンで、もう一つは洗練されたデータ構造を使ってフローネットワークの全域木を管理することで反復と全域木の更新を対数時間で行うバージョンです。これまでに知られている最速のアルゴリズムが最適であると思ってはいけません。最大フローは現在でも活発に研究が行われている領域です。

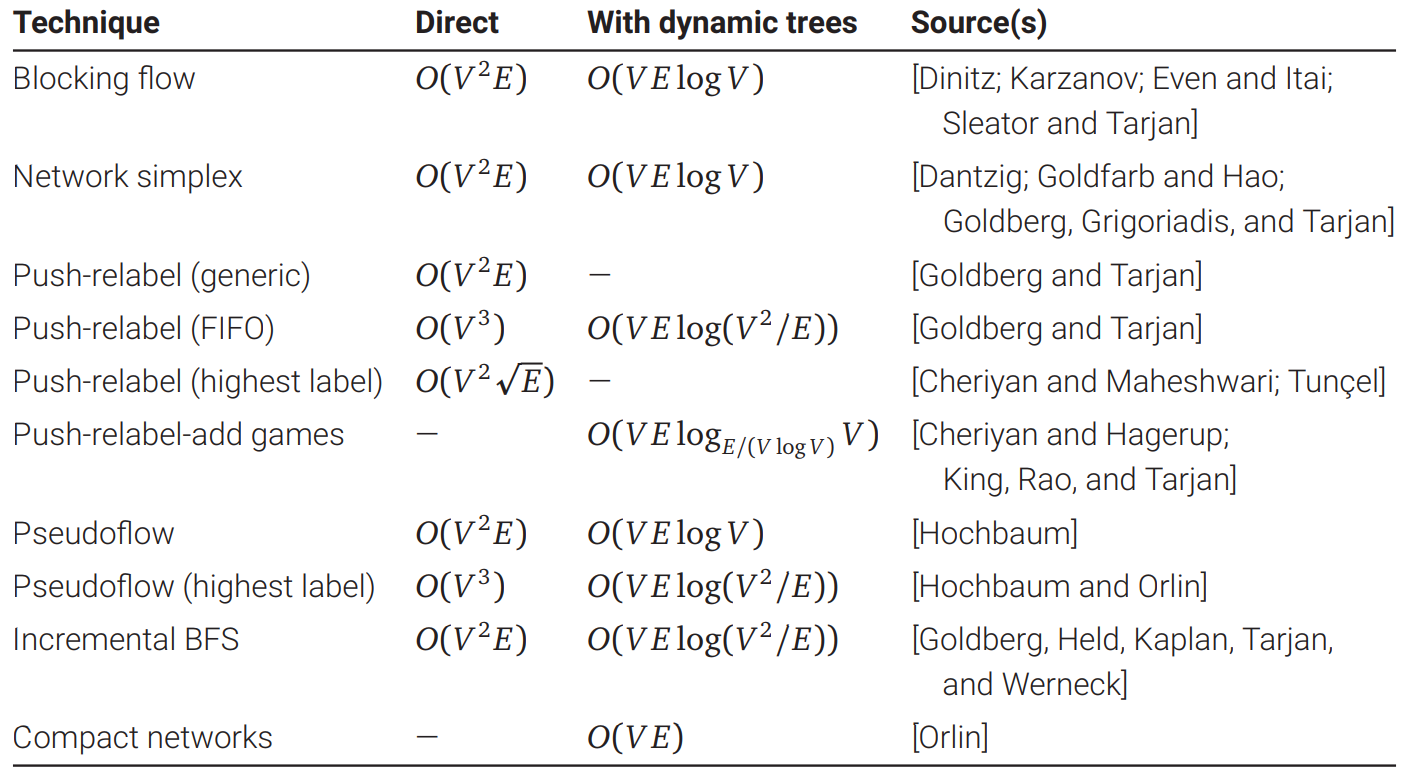
現在知られている (purely combinatorial な) 最速の最大フローアルゴリズムは、2012 年に James Orlin (ジェームス・オーリン) によって発表されたものです。実行時間は \(\pmb{O(VE)}\) であり、フロー分解の最悪計算時間と同じです。このアルゴリズムはそれまでに発見されたアルゴリズムやデータ構造をブラックボックスとして使っており、それらのほとんどがとても複雑なので、Orlin のアルゴリズムの詳細はこの本の範囲を大きく超えます。また Orlin のアルゴリズムを拡張すると、具体的なフロー分解を構築しないアルゴリズムが得られます。実際このアルゴリズムは \(O(V)\) 個しか辺を持たないグラフに対しては実行時間が \(O(V^{2} / \log V)\) となります！

しかしもちろん、最大フローアルゴリズムを使うアルゴリズムの解析においては、この実行時間の上界を使って構いません。次の文章をチートシートに書いておいて宿題で使いましょう:

最後に、全ての辺の容量が \(1\) であるような "単位容量" ネットワークに対するさらに高速な最大フローアルゴリズムを紹介します。1973 年、Alexander Karzanov (アレキサンダー・カルザノフ) は Dinitz (ディニッツ) の blocking-flow アルゴリズム ――上の表で一番上にあるもの―― が単位容量という条件の下では \(O(\min \lbrace V^{2 / 3}, E^{1 / 2} \rbrace E)\) 時間で実行されることを示しました (この実行時間はフロー分解に \(\Omega(VE)\) 時間かかるという事実と矛盾するように見えますが、Karzanov の解析からは単位容量のネットワークは \(O(\min \lbrace V^{2 / 3}, E^{1 / 2} \rbrace E)\) 時間で路に分解できることが分かります)。このアルゴリズムは 40 年以上にわたって単位容量のネットワークに対する最速の最大フローアルゴリズムでしたが、この記録は 2014 年 に Aleksander Mądry (アレクサンダー・モドリー) よって破られました。Mądry が示した真に驚くべきアルゴリズムの実行時間は \(O(E^{10/7} \text{polylog } E)\) です。ここでも Mądry のアルゴリズムの詳細はこの本の範囲を大きく超え、正直なところ著者の技量も追いついていません。

1. 表を小さくまとめるために、実行時間が辺の容量や最大フローの値に依存しているアルゴリズムは意図的に除外しました。この制限を考えたとしても、この表は全く不完全です！^[return]