タプル選択

二部グラフの最大マッチングは私がタプル選択 (tuple selection)¹ と呼ぶ問題クラスの一番簡単な例です。タプル選択問題の入力は要素に重複がない有限集合 \(X_{1}, X_{2}, \ldots, X_{d}\) であり、出力は容量に関する次の条件を満たす最大の \(d\)-タプルの集合です:

• 全ての添え字 \(i\) に対して、各 \(x \in X_{i}\) がタプルに現れていいのは \(c(x)\) 回まで。
• 全ての添え字 \(i\) に対して、各 \(x \in X_{i}\) と \(y \in X_{i+1}\) がタプルに現れていいのは \(c(x,y)\) 回まで。

上界 \(c(x)\) と \(c(x,y)\) は (通常は小さな) 非負整数あるいは \(\infty\) です。

二部グラフの最大マッチング問題では \(d=2\)、全ての要素 \(x\) について \(c(x)=1\) 、全ての組 \((x, y)\) について辺 \(xy\) があるなら \(c(x,y)=1\) で辺がないなら \(c(x,y)=0\) です。

与えられる集合が一列に並んでいて、容量の制約が隣接した集合 \(X_{i}\) と \(X_{i+1}\) だけを考えること²を利用すれば、タプル選択問題を次のように定義されるグラフ \(G\) における最大フロー問題に帰着させることができます:

• \(G\) には \(X_{i}\) の各要素に対応する頂点があり、その他にソース頂点 \(s\) とシンク頂点 \(t\) がある。\(s\) と \(t\) を除く各頂点 \(x\) は容量 \(c(x)\) を持つ。

• \(G\) には全ての \(w \in X_{1}\) に対して容量 \(1\) の辺 \(s \rightarrow w\) があり、全ての \(z \in X_{d}\) に対して容量 \(1\) の辺 \(z \rightarrow t\) が存在ある。そして全ての添え字 \(i\) に対して全ての \(x \in X_{i}\) と \(y \in X_{i+1}\) の間に容量 \(c(x,y)\) の辺 \(x \rightarrow y\) がある (\(c(x,y)=0\) である辺 \(x \rightarrow y\) は存在しないとしてもよい)。

\(s\) から \(t\) への任意の路は選択可能な \(d\)-タプルを表します (路がタプルそのものだとも言えます)。逆に制約を満たす \(d\)-タプルは \(G\) における \(s\) から \(t\) への路を表します (タプルが路そのものだとも言えます)。

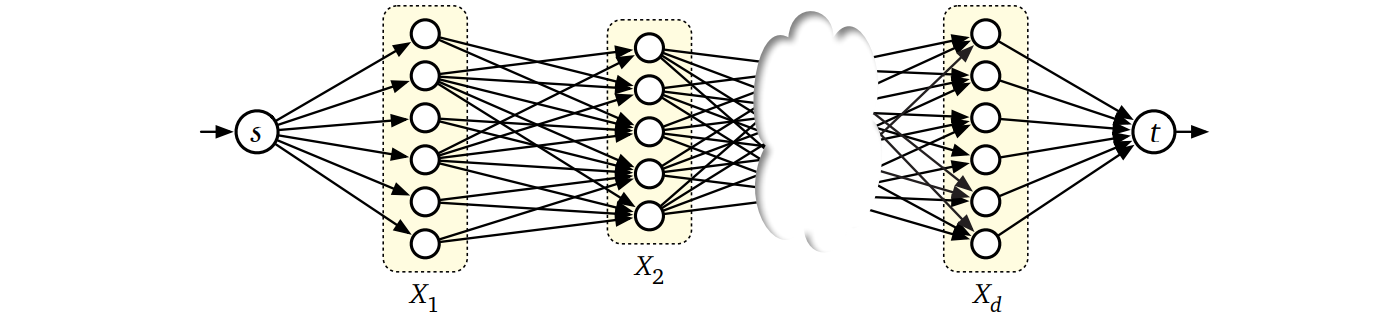
より一般的に議論をするために、\(G\) における任意の実現可能な \((s,t)\)-フローを \(f\) とします。容量は整数または \(\infty\) なので、フロー分解定理より \(f\) は \(s\) から \(t\) への一単位のフローが流れる路 \(|f|\) 個の和として書くことができます。定義を追っていけばこれらの路が表すタプルの集合が容量に関する制約を満たすことが示せます。逆に容量に関する制約を満たす \(k\) 個のタプルに対して、対応する路の和は値が \(k\) の実現可能な \((s,t)\)-フローとなります。

したがって容量に関する制約を満たす最大のタプルの集合は、\(G\) の最大フロー \(f^{\ast}\) を計算すれば見つけることができます。なぜなら \(G\) に含まれる有限の重みが整数であることから一般性を失うことなく \(f^{\ast}\) が整数フローであると仮定でき、よって (一つ前の段落から) \(f^{\ast}\) は \(|f^{\ast}|\) 個の制約を満たすタプルに対応するからです。

試験のスケジューリング

次に説明する "現実世界の" スケジューリング問題を見れば、一般的な帰着をよりよく理解できるかもしれません。

あなたは Sham-PooBanana 大学に雇われて期末試験のスケジュールを立てるアルゴリズムを設計することになりました。\(n\) 個の講義の期末試験が行われる時と場所を、 \(t\) 個の時間帯と \(r\) 個の教室から決めなければなりません。ある時間帯にある教室で行える試験は最大でも一つであり、試験を複数の時間帯・教室に分けて行うことはできません。また各試験には試験監督³が一人着く必要があり、試験を監督できる人物は \(p\) 人いて、それぞれ監督可能な時間帯が異なっています。またどの試験監督も合計で 5 個より多い試験を監督することはできません。

このスケジューリング問題の入力は三つの配列です:

• 整数の配列 \(E[1..n]\): \(E[i]\) が \(i\) 番目の講義の試験に出席する学生の数を表す。
• 整数の配列 \(S[1..r]\): \(S[j]\) が \(j\) 番目の教室の座席数を表す。\(i\) 番目の講義の試験が \(j\) 番目の教室で行えるのは \(E[i] \leq S[j]\) が成り立つときだけ。
• 真偽値の配列 \(A[1..t, 1..p]\): \(A[k,l] = \textsc{True}\) は \(l\) 番目の試験監督が \(k\) 番目の時間帯に試験を監督できることを表す⁴。

\(N = n + r + tp\) で入力サイズを表すとします。あなたの仕事は教室、時間帯、試験監督を全ての期末試験に割り当てるか、そのような割り当てが不可能であると正しく報告するアルゴリズムを設計することです。

この問題は典型的なタプル選択問題であり、四つの集合が登場します: 講義、教室、時間帯、そして試験監督の集合です。この問題を解くために、六種類の頂点 ――ソース頂点 \(s^{\prime}\), 講義を表す頂点 \(c_{i}\), 教室を表す頂点 \(r_{j}\), 時間帯を表す頂点 \(t_{k}\), 試験監督を表す \(p_{l}\), シンク頂点 \(t^{\prime}\)―― および五種類の辺を持つフローネットワーク \(G\) を構築します:

• 全ての講義 \(i\) について容量 \(1\) の辺 \(s^{\prime} \rightarrow c_{i}\) が存在する (「全ての講義は最大でも一つの期末試験を持つ」)。
• 教室 \(i\) と講義 \(j\) が \(E[i] \leq S[j]\) を満たすときに限って辺 \(c_{i} \rightarrow r_{i}\) が存在し、その容量は \(\infty\) である (「講義 \(i\) が教室 \(j\) で試験を行えるのは教室に十分な席があるときだけ」)。講義の生徒数 \(E[i]\) と教室の座席数 \(S[j]\) が使われるのはここだけ。
• 全ての教室 \(j\) と時間帯 \(k\) に対して容量 \(1\) の辺 \(r_{j} \rightarrow t_{k}\) が存在する (「教室 \(j\) で時間帯 \(k\) に行われる試験は最大でも一つ」)。
• \(A[k,l] = \textsc{True}\) であるような時間帯 \(k\) と試験監督 \(l\) に対して容量 \(1\) の辺 \(t_{k} \rightarrow p_{l}\) が存在する (「試験監督は監督可能な時間帯に最大一つの試験を監督できる」)。
• 全ての試験監督 \(l\) に対して容量 5 の辺 \(p_{l} \rightarrow t^{\prime}\) が存在する (「試験監督が監督できる試験は最大 5 個」)。

(ソース頂点とシンク頂点を \(s^{\prime}, t^{\prime}\) と呼んでいるのは問題文で \(t\) が時間帯の数を表すために既に使われているからであり、そうしなければいけない特別な理由はありません) まとめると、\(G\) は \(n + r + t + p + 2 = O(N)\) 個の頂点と \(O(nr + rt + tp) = O(N^{2})\) 個の辺を持ちます。

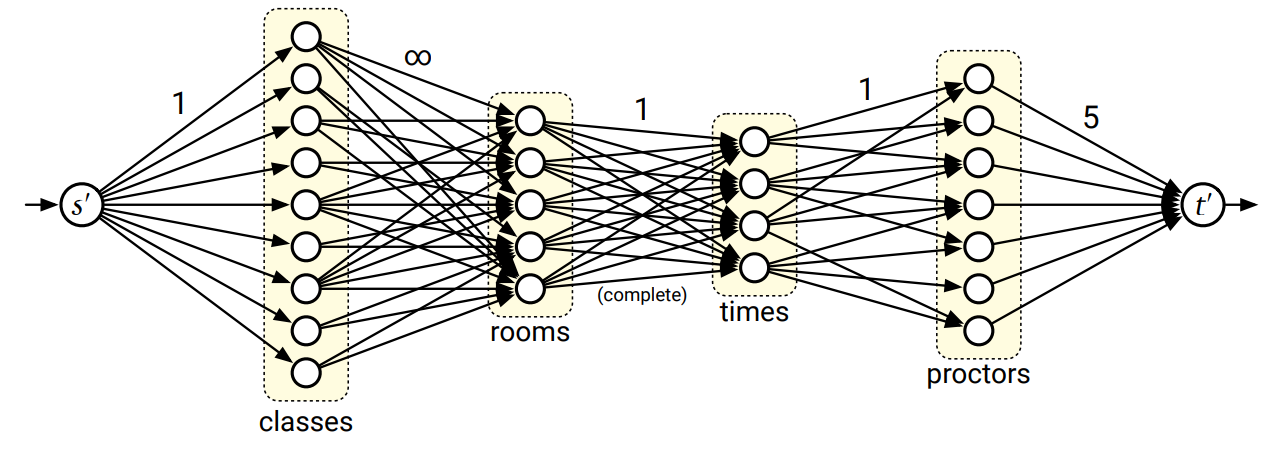
\(G\) における \(s^{\prime}\) から \(t^{\prime}\) への路は、一つの期末試験に対する制約を満たす講義、教室、時間帯、試験監督の組を表します。つまり講義を取っている全ての生徒は教室に収まり、試験監督はその時間帯に試験を監督できるということです。逆に正しい (講義、教室、時間帯、試験監督の) 組には対応する \(s^{\prime}\) から \(t^{\prime}\) への路が \(G\) に存在します。よって行う試験の数を最大化するような制約を満たすスケジュールを構築するには、まず \(G\) における最大 \((s^{\prime},t^{\prime})\)-フローを計算して、それから最大フローに含まれる路を講義、教室、時間帯、試験監督の組に変換すれば良いことになります。もし \(|f^{\ast}| = n\) ならば計算されたスケジュールを返し、そうでなければ \(n\) 個の期末試験を行うスケジュールが不可能だと正しく報告します。

入力データから \(G\) を総当たりで作るのには \(O(E)\) 時間かかり、最大フロー \(f^{\ast}\) は \(|f^{\ast}| \leq n < V\) を満たすので Ford-Fulkerson のアルゴリズムまたは Orlin のアルゴリズムを使って \(O(VE)\) 時間で計算でき、フロー分解は \(O(VE)\) 時間で計算できます。したがって、この問題を解くアルゴリズム全体の実行時間は \(O(VE) = \pmb{O(N^{3})}\) です。

1. この問題に対する標準的な名前を見つけられなかったので、タプル選択という言葉は自分で作りました。この問題が「割り当て問題 (assignment problem)」と呼ばれることもありますが、この言葉が指すのは辺に重みの付いた二部グラフに対する最大重み二部マッチングを求める問題であることが多いです。^[return]

2. 隣り合わない集合の組 (\(j > i + 1\) に対する \(X_{i}\) と \(X_{j}\)) に関する制約が一つでもあった場合、この問題は \(\textsc{Exact3Dimenstional}\)\(\textsc{Matching}\) からの簡単な帰着によって NP 困難となります。NP 困難性については次の章で扱います。^[return]

3. アメリカなら proctor、アメリカ以外なら invigilator と呼ばれます。^[return]

4. この情報を最初からグラフで表した方が良いのは間違いないのですが、そうすると帰着が分かりにくくなると私は考えました。^[return]