メモ化と動的計画法
トポロジカルソートを使うと多くの動的計画法のアルゴリズムを表現できます。ここでは例として依存グラフを考えます。以前触れた通り、再帰方程式の依存グラフ (dependency graph) とは、頂点が再帰的な小問題に対応する有向グラフであって、小問題同士を結ぶ辺があるのは始点の問題を解くときに終点の問題の答えが必要になるときだけであるものです。依存グラフに閉路があるとナイーブな再帰的アルゴリズムが停止しなくなるので、依存グラフは必ず非巡回です。
メモ化を使った再帰方程式の評価は依存グラフに対する深さ優先探索と全く同じです。具体的には、依存グラフの頂点に "印が付いている" ことが、その頂点の表す小問題の答えが計算されていることに対応し、ブラックボックスなサブルーチン \(\textsc{PreVisit}\) と \(\textsc{PostVisit}\) が実際の計算に対応します:
procedure \(\texttt{Memoize}\)(\(x\))
if \(value[x]\) が未定義 then
\(value[x]\) を初期化する
\({}\)
for \(x\) が依存する小問題 \(y\) do
\(\texttt{Memoize}\)(\(y\))
\(value[y]\) で \(value[x]\) を更新する
\(value[x]\) の最終処理をする
procedure \(\texttt{DFS}\)(\(v\))
if \(v\) に印が付いていない then
\(v\) に印をつける
\(\texttt{PreVisit}\)(\(x\))
for 全ての辺 \(v \rightarrow w\) do
\(\texttt{DFS}\)(\(w\))
\({}\)
\(\texttt{PostVisit}\)(\(x\))
この対応関係についてさらに考えると、動的計画法を使った再帰方程式の評価が、依存グラフに対するトポロジカル順序の逆順の評価に対応することが分かります ――全ての小問題は依存する小問題が計算された後に計算されるからです。よって全ての動的計画法のアルゴリズムは、計算する再帰方程式の依存グラフの帰りがけ順走査に等しくなります!
procedure \(\texttt{DynamicProgramming}\)(\(G\))
for 帰りがけ順の小問題 \(x\) do
\(value[x]\) を初期化する
for \(x\) が依存する小問題 \(y\) do
\(value[y]\) で \(value[x]\) を更新する
\(value[x]\) の最終処理をする
ただし動的計画法とトポロジカルソートの間には微妙な違いがあります。まず、ほとんどの動的計画法のアルゴリズムにおいて依存グラフは明示的に定義されません。つまり頂点と辺が実際にメモリ上に格納されるのではなく、再帰方程式によって陰に表されます。しかしある問題が依存する再帰的な小問題を定数時間で列挙できるという条件の下では依存グラフが存在するかのように処理を行えるので、実際のアルゴリズムがこの違いに大きく影響されることはありません。
もう一つのもっと重要な違いは、動的計画法の依存グラフのほとんどは構造化されているという点です。例えば五章で説明した編集距離問題に対する依存グラフは完全な格子に対角線が入ったものであり、最適二分探索木問題に対する依存グラフは直角三角形に右または上方向の辺が付いたものです。この周期的な構造のおかげで、動的計画法の依存グラフのトポロジカル順序 (の逆順) はネストされた for ループを使ってアルゴリズムの中に組み込むことができます。これまではこのトポロジカル順序のことを「破綻しない評価順序」と呼んでいました。
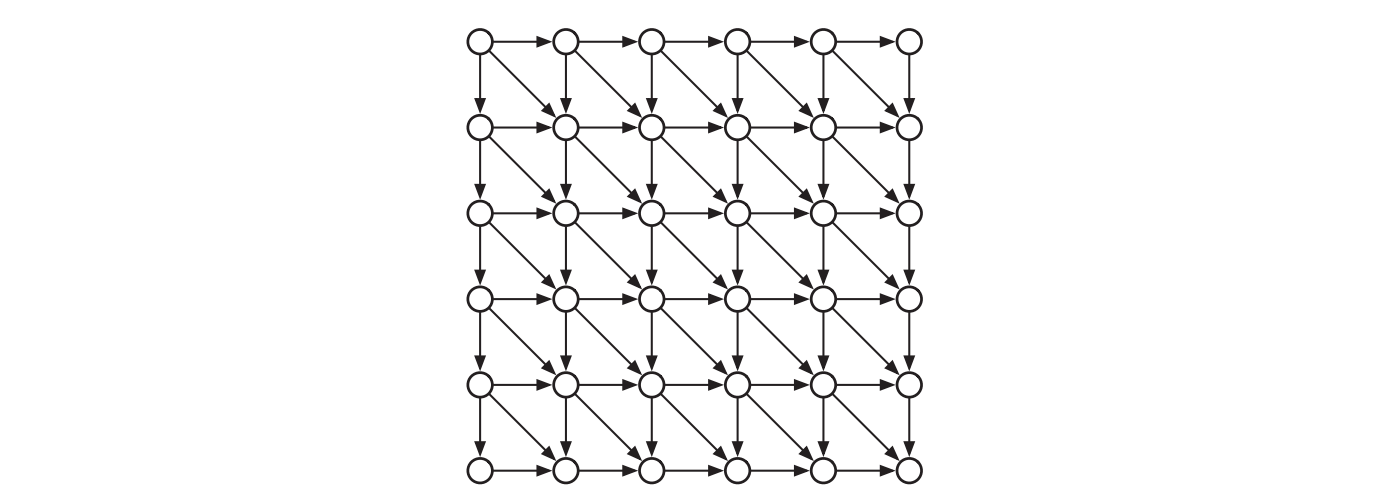
DAG の上での動的計画法
逆に言えば、構造化されていない依存グラフを持つ問題に対する動的計画法のアルゴリズムを深さ優先探索を使って作ることができます。例として、辺が長さを持つ有向グラフ \(G\) における頂点 \(s\) から \(t\) への有向路で長さが最大のものを求める最長路 (longest path) 問題を考えます。一般の有向グラフに対する最長路問題は巡回セールスマン問題からの簡単な帰着で NP 完全であることが示せますが、\(G\) が非巡回の場合には線形時間の簡単な解法が存在します。
与えられた終点を \(t\) とし、\(v\) を任意の頂点とします。\(G\) における \(v\) から \(t\) への最長路の長さを \(LLP(v)\) とします。\(G\) が DAG ならば、次の再帰方程式が成り立ちます: \[ LLP(v) = \begin{cases} 0 & \text{if } v = t \\ \max \lbrace l(v \rightarrow w) + LLP(w)\ |\ v \rightarrow w \in E \rbrace & \text{それ以外} \end{cases} \] ここで \(l(v \rightarrow w)\) は辺 \(v \rightarrow w\) の重み (ここでは"長さ") を表し、\(\max \varnothing = - \infty\) です。例えば \(v\) が \(t\) と異なるシンク頂点なら \(LLP(v) = -\infty\) です。
この再帰方程式に対する依存グラフは入力グラフ \(G\) 自身です。 なぜなら、小問題 \(LLP(v)\) が \(LLP(w)\) に依存することが辺 \(v \rightarrow w\) が存在することと同値だからです。したがって頂点 \(s\) から始まる \(G\) の深さ優先探索を使えばこの再帰的関数を \(O(V+E)\) 時間で評価できます。次のアルゴリズムは各頂点に対する最長の長さ \(LLP(v)\) を追加のフィールド \(LLP\) に保存します:
procedure \(\texttt{LongestPath}\)(\(v, t\))
if \(v = t\) then
return 0
if \(v.LLP\) が定義されていない then
\(v.LLP \leftarrow - \infty\)
for \(v \rightarrow w\) の形をした辺 do
\(v.LLP \leftarrow \max \lbrace v.LLP,\ l(v \leftarrow w) + \textsc{LongestPath}(w,t) \rbrace\)
return \(v.LLP\)
今までに説明したことを使えば、このメモ化付き再帰的アルゴリズムをトポロジカルソートを使って書き直して、動的計画法のアルゴリズムを得ることができます。
procedure \(\texttt{LongestPath}\)(\(s, t\))
for 帰りがけ順の頂点 \(v\) do
if \(v = t\) then
\(v.LLP \leftarrow 0\)
else
\(v.LLP \leftarrow - \infty\)
for \(v \rightarrow w\) の形をした辺 do
\(v.LLP \leftarrow \max \lbrace v.LLP,\ l(v \rightarrow w) + w.LLP \rbrace\)
return \(s.LLP\)
二つのアルゴリズムは同一と言ってもよいでしょう ――最初のアルゴリズムにおける再帰と、二つ目のアルゴリズムにおける for ループが "同じ" 深さ優先探索を表すのです!どちらを選ぶかは完全に好みの問題です。
動的計画法の問題のうち最適な決断の列 (decision sequence) を作るものはほとんど常に、特定の DAG における最適路を見つける問題に置き換えることができます。例えば二章と三章で扱った文字列分割、部分和、最長増加部分列、編集距離の問題は全て、頂点や辺に重みの付いた DAG において最長または最小の路を見つける問題に変形でき、その DAG とは元の問題の依存グラフです。一方で最適二分探索木や木の最大独立集合を見つける問題のような、"木の形をした" 動的計画法の問題は、DAG における最適路を見つける問題に変形できません。