重要な変種

スタック: 深さ優先

"袋" としてスタックを使って何か優先探索を実装した場合、以前に紹介した深さ優先探索となります。スタックでは挿入 (プッシュ) と削除 (ポップ) をそれぞれ \(O(1)\) 時間で行えることから、アルゴリズム全体の実行時間は \(\pmb{O(V + E)}\) です。親へ向かう辺を集めることで形成される全域木は深さ優先全域木 (depth-first spanning tree) と呼ばれます。この全域木の正確な形は探索を始める頂点と for ループにおいて辺を選ぶ順番に依存しますが、一般的に言って、深さ優先全域木は細長い形になります。深さ優先探索の重要な特徴と応用については六章で見ます。

キュー: 幅優先

"袋" としてキューを使って何か優先探索を実装した場合、幅優先探索 (breadth-first search, BFS) と呼ばれる別のグラフ走査アルゴリズムとなります。キューは挿入 (プッシュ) と削除 (プル) をそれぞれ \(O(1)\) で行えるので、アルゴリズム全体の実行時間は \(\pmb{O(V + E)}\) です。この場合、親への辺を集めた全域木は幅優先全域木 (breadth-first spanning tree) と呼ばれます。また \(s\) 以外の各頂点から親への辺をたどっていくと \(s\) からその頂点への最短路が手に入ります。最短路問題については八章で扱います。幅優先全域木の正確な形はここでも探索を始める頂点と for ループ において辺を選ぶ順番に依存しますが、一般的に言って、幅優先全域木の形は短いブラシ状になります。

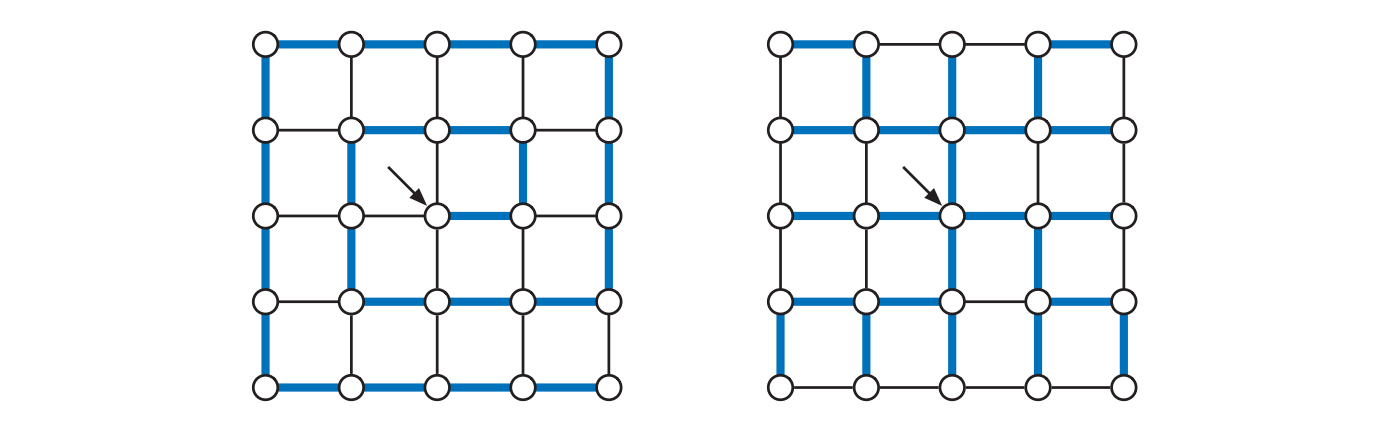
優先度付きキュー: 最良優先

最後の例は "袋" として優先度付きキューを使って何か優先探索を実装する場合で、このときに手に入るのは最良優先探索 (best-first search) と呼ばれるアルゴリズムのクラスです。優先度付きキューには全ての辺が最大で一回ずつ格納され、辺の追加および優先度が最低の辺の取り出しには \(O(\log E)\) 時間かかるので、最良優先探索の実行時間は \(\pmb{O(V + E \log E)}\) です。

最良優先探索をアルゴリズムの "クラス" と言ったのは、辺に優先度を付ける方法がいくつかあり、異なる優先度の付け方によって異なるアルゴリズムが手に入るためです。ここではよく知られた変種を三種類紹介します。これから紹介するアルゴリズムでは、全ての辺 \(uv\) または \(u \rightarrow v\) が非負の重み \(w(uv)\) または \(w(u \rightarrow v)\) を持っているとします。

まず、無向グラフの入力に対して辺の重みを優先度として使った場合、最良優先探索は \(s\) の属する成分の最小全域木 (minimum spanning tree) を構築します。意外なことに、全ての辺の重みが異なっているならば、最小全域木の形は探索を始める頂点や隣接する頂点を調べる順番に依存しません: このような条件では最小全域木が唯一となります。最良優先のこのインスタンスは通常 Prim (プリム) のアルゴリズムとして知られています (が、ここでも名前は正しくありません)。このアルゴリズムと他の最小全域木アルゴリズムは七章で扱います。

次に、路の長さを辺の重みの和として定義し、この長さを優先度として最良優先探索を行うと、\(s\) から各頂点への最短路 (shortest path) を計算できます。このアルゴリズムでは印の付く頂点 \(v\) に対して距離 \(\mathit{dist}(v)\) が記録されます。最初 \(s\) に対しては \(\mathit{dist}(s) = 0\) とします。他の全ての頂点 \(v\) に対しては \(\mathit{parent}(v) \leftarrow p\) とするときに \(\mathit{dist}(v) \leftarrow \mathit{dist}(p) + w(p \rightarrow v)\) と設定し、優先度付きキューに辺 \(v \rightarrow w\) を挿入するときには優先度として \(\mathit{dist}(v) + w(v \rightarrow w)\) を使います。辺の重みが正であれば、 \(\mathit{dist}(v)\) には \(s\) から \(v\) への最短路の長さが記録されます。最良優先探索のこのインスタンスは Dijkstra (ダイクストラ) のアルゴリズムとして知られています (が、ここでも厳密に言えば名前は正しくありません)。このアルゴリズムは八章で扱います。

最後に考えるのは、路の幅を路に含まれる辺の重みの最小値と定義し、この幅を優先度とした場合です。Djkstra の最良優先探索アルゴリズムを少しだけ変更したこのアルゴリズムが計算するのは最幅路 (widest path)、またの名をボトルネック最短路 (bottleneck shortest path) です。このアルゴリズムでは印の付く頂点 \(v\) に対して \(\mathit{width}(v)\) という値が記録されます。最初 \(s\) に対しては \(\mathit{width}(s) = \infty\) とし、他の頂点 \(v\) に対しては、\(\mathit{parent}(v) \leftarrow p\) とするときに \(\mathit{width}(v) \leftarrow \min \lbrace \mathit{width}(p), w(p \rightarrow v) \rbrace\) と設定します。そして優先度付きキューに辺 \(v \rightarrow w\) を挿入するときには優先度として \(\min \lbrace \mathit{width}(v), w(v \rightarrow w) \rbrace\) を使います。最幅路は最大フローを計算するときに利用します。最大フローについては (お分かりでしょうが) 十章で扱います。

非連結グラフ

\(\textsc{WhateverFirstSearch}\) は探索を始める \(s\) から到達可能な頂点だけを訪れます。そのため \(G\) の全ての点を訪れるには、次に示す簡単な "ラッパー" 関数が必要になります:

あなたが質問するのが聞こえます: 「ちょっと待った。なぜそんな複雑にする必要が？ 頂点配列を走査すればそれで終わり¹では？」

ええ、こうすることもできます。ただしこれができるのは頂点の完全なリストがあるときだけです。グラフの中には頂点の明示的なリストを持たないグラフもあります²。さらに重要なこととして、仮に頂点のリストがあった場合でも、このナイーブなアルゴリズムでは頂点を訪れる順番が "袋" として使われるデータ構造だけで決まってしまい、グラフの抽象的な構造が順番に反映されなくなってしまいます。

具体的に言うと、\(\textsc{WFSAll}\) はまずある成分に含まれる全ての頂点を訪れ、その次に別の成分を訪れる、というふうに全ての成分を調べます。この順番を利用すれば、非連結グラフの成分の数を単純なカウンターを使って数えることができます。これはナイーブなアルゴリズムでは不可能です:

もう少し頑張れば、全ての頂点に印をつける代わりに、全ての頂点がどの成分に属しているかを記録することもできます:

\(\textsc{WFSAll}\) は全ての頂点に一回ずつ印をつけ、全ての辺を一回ずつ袋に入れ、全ての辺を袋から一回ずつ袋から取り出すので、全体の実行時間は \(O(V + ET)\) です。ここで \(T\) は袋を使った操作の実行時間です。具体的に言うと、深さ優先探索と幅優先探索ではアルゴリズムの実行時間は \(O(V+E)\) であり、\(\textsc{WhateverFirstSearch}\) と同じです。

\(\textsc{WhateverFirstSearch}\) が一つの成分の全域木を計算することから、\(\textsc{WFSAll}\) を使えばグラフの全域森を計算できます。特に、辺の重さを優先度に使う最良優先探索は最小重み全域森を \(O(V + E \log E)\) で計算します。

驚く外ないのですが、少なくとも一つのとても有名なアルゴリズムの教科書には、このラッパー関数を使うことができるのが深さ優先探索だけであると書かれています³。これは完全な間違いです。歴史を見れば、1945 年に Konrad Zuse (コンラート・ツーゼ) がまだ実装の存在しなかったプログラミング言語 Plankalkül (プランカルキュール) で書いた世界初の幅優先探索の実装は、無向グラフの成分を数えてラベル付けするために作られています。

有向グラフ

何か優先探索を有向グラフに適用するのは簡単です。唯一の違いは頂点に印をつけた後に袋に入れるのがその頂点の後者であるという点です。実は、標準的な隣接リストまたは隣接行列を使っているなら、無向グラフに対するアルゴリズムのコードをそのまま有向グラフに使うことができます！

前述の証明により、このアルゴリズムが \(s\) から到達可能な全ての頂点に印をつけること、そして有向辺 \(\mathit{parent}(v) \rightarrow v\) の集合が全ての辺が根 \(s\) から遠ざかる根付き木を定義することが言えます。しかし、仮にグラフが連結だったとしても、グラフの全域木が計算できるとは限りません。有向グラフにおいては到達可能性が対称でないからです。

一方で、\(\textsc{WhateverFirstSearch}\) は \(s\) から到達可能な頂点の全域木なら定義します。さらに "袋" のインスタンスを変えれば、到達可能な頂点に対する深さ優先全域木、幅優先全域木、最小重み全域有向木、最短路木、最幅路木が手に入ります。

1. この言葉 ("just") はほとんど常に、あなたが何か重要なことを見落としていることを示します。^[return]

2. 一方で、各頂点に印が付いた時刻を記録するようにすれば、"全ての頂点の印を消す" という操作は走査を開始するときに時間を更新することで頂点の数に関係なく \(O(1)\) で行えます。この場合頂点に "印が付いている" ことはその頂点に記録された時刻が走査の開始時間よりも遅いことで表されます。^[return]

3. 直接引用すれば: "Unlike breadth-first search, whose predecessor subgraph forms a tree, the predecessor subgraph produced by a depth-first search may be composed of several trees, because the search may repeat from multiple sources." (幅優先探索では前者部分グラフが木を形成する。これに対して、深さ優先探索の前者をたどるグラフは複数の木を形成できる。深さ優先探索は複数の異なる成分に属する頂点を始点として行えるからである)^[return]