講義のスケジューリング
次の例はもう少し複雑です。あなたは情報科学をドロップアウトして応用カオス理論を専攻することに決めたとします。応用カオス理論専攻では全ての講義が毎週同じ日に開校されており、この日は学生から「Soberday (素面日)」と呼ばれていました (興味深いことに、学部はこの名前を使いませんでした)。講義はそれぞれ異なった開始時刻と終了時刻を持ちます: 例えば AC 101 (トイレットペーパー景観設計 "Toilet Paper Landscape Architecture") は 10:27 pm に始まって 11:51 pm に終わり、AC 666 (終末の内在化 "Immanentizing the Eschaton") は 4:18 pm に始まって 4:22 pm に終わる、などです。できるだけ早く卒業したいあなたは、なるべく多くの講義を取りたいとします (応用カオス理論専攻の講義では履修さえすれば何もしなくても単位が取得できます)。大学の履修登録用コンピューターは時間が被っている講義を取らせてくれず、この "機能" を書き換えてくれる友達も見当たりません。取るべき講義はどれでしょうか?
きちんと言うと、講義の開始時刻と終了時刻が入った二つの配列 \(S[1..n]\) と \(F[1..n]\) が与えられ、ある実数 \(M\) があって全ての \(i\) に対して \(0 \leq S[i] \leq F[i] \leq M\) が成り立つとします (例えば \(M\) は Soberday の長さをピコ秒で表したものだったりします)。この問題で求めるのは \(X \subset \lbrace 1,2,\ldots,n \rbrace\) であって任意の組 \((i,j) \in X\) に対して \(S[i] > F[j]\) または \(S[j] > F[i]\) が成り立つものの中で最大のものです。
この問題を図示すると以下のようになります。講義が長方形によって表され、\(x\) 軸座標の左端と右端がそれぞれ講義の開始時刻と終了時刻を表します。垂直方向に重ならない長方形の部分集合で一番大きいものを見つけることが目標となります。

講義は取るか取らないかのどちらかなので、この問題には単純な再帰的解法があります。講義 \(1\) が始まる前に終わる講義の集合を \(B\) 、講義 \(1\) が終わった後に始まる講義の集合を \(A\) とします: \[ \begin{aligned} B & := \lbrace i \ | \ 2 \leq i \leq n \text{ かつ } F[i] < S[1] \rbrace \\ A & := \lbrace i \ | \ 2 \leq i \leq n \text{ かつ } F[1] < S[i] \rbrace \end{aligned} \] もし最適なスケジュールに講義 \(1\) が含まれるならば、部分集合 \(B\) と \(A\) に対する最適スケジュールも全体の最適なスケジュールに含まれ、この二つの最適なスケジュールは再帰的に見つけることができます。もしそうでなくて最適なスケジュールに講義 \(1\) が含まれないならば、全体の最適なスケジュールは \(\lbrace 2, 3, \ldots, n \rbrace\) から再帰的に見つけることができます。この再帰的なアルゴリズムに対して動的計画法を適用すると実行時間が \(O(n^{3})\) となりますが、ここでは詳細には踏み入りません。もっと速くできるからです1。
直感的に分かるのは、最初選ぶ講義はなるべく早く終わった方がその後に選択できる講義の選択肢が増えるということです。この直感を使うと、次の単純な貪欲アルゴリズムが作れます: 「全ての講義を終了時刻が早い順にチェックしていって、これまでの選択と矛盾しない講義を見つけたら、取る!」 この貪欲アルゴリズムの動作を次に示します:
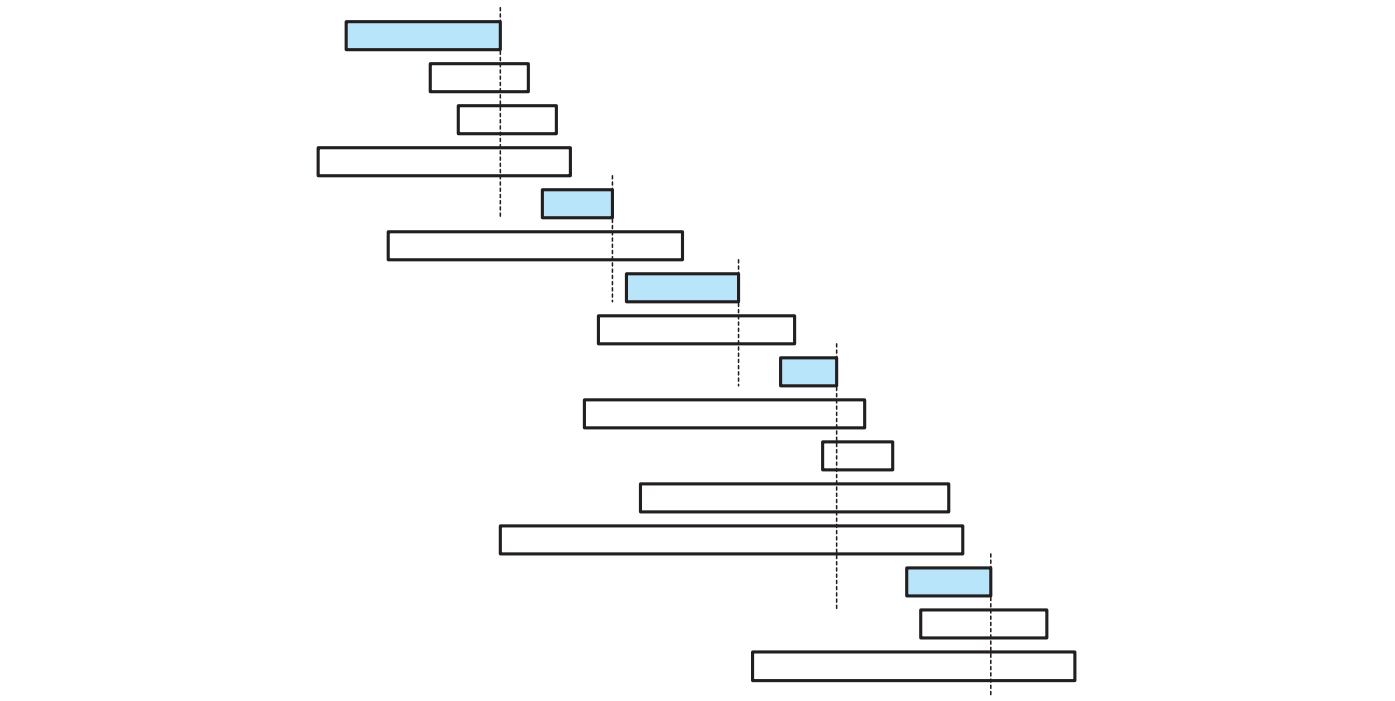
このアルゴリズムをもう少しきちんと書くと次の疑似コードとなります (最初の行が理解できることを願います)。最初のソート後は線形時間で実行できる単純なループがあるだけなので、アルゴリズムの実行時間は最初のソートに支配されることになり、\(O(n \log n)\) です。
procedure \(\texttt{GreedySchedule}\)(\(S[1..m], F[1..n]\))
\(F\) をソートして \(S\) をその結果に合うように並べ替える
\(\mathit{count} \leftarrow 1\)
\(X[\mathit{count}] \leftarrow 1\)
for \(i \leftarrow 2\) to \(n\) do
if \(S[i] > F[X[\mathit{count}]]\) then
\(\mathit{count} \leftarrow \mathit{count} + 1\)
\(X[\mathit{count}] \leftarrow i\)
return \(X[1..\mathit{count}]\)
\(\textsc{GreedySchedule}\) が衝突しない最大のスケジュールを本当に計算することを示すには、テープのソートのときと同じような交換を使った議論 (exchange argument) を使います。ここで注意すべきなのは、示すべき命題が「貪欲なスケジュールが唯一の最大スケジュールである」ではない点です (上の二つの図を見比べてみてください!)。 示すことができるのは「少なくとも一つの最適なスケジュールが貪欲アルゴリズムによって作られる」です。
命題 4.3 少なくとも一つの衝突しない最大スケジュールは一番早くに終了する講義を含む。
証明 最初に終了する講義を \(f\) とする。衝突しない最大スケジュールで \(f\) を含まないものを \(X\) 、\(X\) で最初の講義を \(g\) とする。 \(f\) の終了時刻は \(g\) よりも早いので、\(f\) は \(X \backslash \lbrace g \rbrace\) の任意の講義と衝突しない。よって \(X^{\prime} = X \cup \lbrace f \rbrace \backslash \lbrace g \rbrace\) は衝突が起こらない。 \(X^{\prime}\) は \(X\) と同じサイズだから、同じく最大である。 \(\Box\)
アルゴリズム全体の正しさの証明には、私たちの旧友である帰納法の助けを借ります。
定理 4.4 貪欲なスケジュールは最適なスケジュールである。
証明 \(f\) を一番早く終了する講義、\(A\) を \(f\) が終了した後に開始する講義の集合とする。一つ前の命題より最適なスケジュールで \(f\) を含むものが存在する。 \(f\) を含む最適なスケジュールは、\(f\) と衝突しない講義すなわち \(A\) に対する最適なスケジュールを持っていなければならない。貪欲なアルゴリズムは \(f\) を選び、そして再帰法の仮定によって \(A\) から最適なスケジュールを選ぶ。したがって貪欲なスケジュールは最適なスケジュールである。 \(\Box\)
この証明は帰納法を少し展開したほうが理解しやすいかもしれません。
証明 貪欲アルゴリズムによって選ばれた講義を開始時間でソートして \(\langle g_{1}, g_{2}, \ldots, g_{k} \rangle\) とする。衝突しない最大スケジュールであって開始時間でソートすると \[ S = \langle g_{1}, g_{2}, \ldots, g_{j-1}, c_{j}, c_{j+1}, \ldots, c_{m} \rangle \] と表せて、\(c_{j}\) が \(g_{j}\) と異なるものが存在すると仮定する (例えば \(j=1\) とするとこのスケジュールは貪欲アルゴリズムが選ばない講義からスタートすることになる)。このスケジュールの構成から、\(j\) 番目の貪欲な選択 \(g_{j}\) はそれまでの講義 \(g_{1}, g_{2}, \ldots, g_{j-1}\) と衝突しない。また \(S\) は衝突しないことから、\(c_{j}\) もそれまでの講義と衝突しない。さらに \(g_{j}\) は \(c_{j+1}, \ldots, c_{m}\) と衝突しないことも言えるので、変更したスケジュール \[ S = \langle g_{1}, g_{2}, \ldots, g_{j-1}, g_{j}, c_{j+1}, \ldots, c_{m} \rangle \] もまた衝突しないことが分かる (この議論は命題 4.3を一般化したものである。命題 4.3 では \(j=1\) だった)。
帰納法によって、貪欲アルゴリズムが選択する講義を全て含む最適なスケジュール \(\langle g_{1}, g_{2}, \ldots g_{k}, c_{k+1}, \ldots, c_{m} \rangle\) が存在することが言える。したがって \(k=m\) でなければならない: もし貪欲アルゴリズムが選ぶ最初の \(k\) 個の講義のどれとも衝突しない講義があるなら、貪欲アルゴリズムは \(k\) 個より多い講義を選んでいなければならない! \(\Box\)
-
ただしそれでも、自分で詳細を詰めてみるべきです。動的計画法を使えば異なる "良い" 基準に沿った "最良" スケジュールを見つけることができますが、貪欲アルゴリズムが見つけられるのは "良い" が "要素の数が多い" を意味するときだけです。また異なる再帰的関係を使えば実行時間を \(O(n^{2})\) にできます。[return]