練習問題

$G = (V,E)$ を有向グラフとし、各頂点の入次数と出次数が等しいとします。$G$ が $u$ から $v$ への大きさ $k$ の辺素路集合を含むとき、$G$ は $v$ から $u$ への大きさ $k$ の辺素路集合を含みますか？証明または反例とその説明を示してください。
無向グラフ $G = (V,E)$ と三つの頂点 $u,v,w$ が与えられたとします。$u$ から $w$ への $v$ を通る路があるかどうかを判定するアルゴリズムを説明、解析してください。 [ヒント: $G$ が有向グラフだとこの問題は NP 困難です！]
有向グラフ $G = (V,E)$ と複数のソース頂点 $s_{1}, s_{2}, \ldots, s_{\sigma}$ と複数のシンク頂点 $t_{1}, t_{2}, \ldots, t_{\tau}$ が与えられたとします。ソースかつシンクである頂点は存在しません。多終端フロー (multi-terminal flow) とは、関数 $f: E \rightarrow \mathbb{R}_{\geq 0}$ であってソースでもシンクでもない全ての頂点において保存条件が満たされるものを言います。多終端フロー $f$ の値 $|f|$ とは全てのソース頂点から出るフローの和です: \[ |f| := \sum_{i=1}^{\sigma} \left(\sum_{w} f(s_{i} \rightarrow w) - \sum_{u} f(u \rightarrow s_{i}) \right) \] 通常のフローと同じように、求めたいのは辺の端点において制約が満たされるフローで最大のものです。フローがどのソース頂点から出るか、あるいはどのシンク頂点へ向かうかは考えません。
1. 多終端フローを計算する次のアルゴリズムを考えます。ここで変数 $f$ と $f^{\prime}$ はフロー関数を表し、サブルーチン $\textsc{MaxFlow}(G, s, t)$ はソース $s$ からシンク $t$ への通常の最大フローを求めます。
  
  procedure $\texttt{MaxMultiFlow}$($G, s[1..\sigma], t[1..\tau]$)
  
  ⟨⟨フローを初期化する⟩⟩
  
  $f \leftarrow 0$
  
  for $i \leftarrow 1$ to $\sigma$ do
  
  for $j \leftarrow 1$ to $\tau$ do
  
  $f^{\prime} \leftarrow$$\texttt{MaxFlow}$($G_{f}, s[i], t[j]$)
  
  ⟨⟨フローを更新する⟩⟩
  
  $f \leftarrow f + f^{\prime}$
  
  return $f$
  
  このアルゴリズムが $G$ の最大多終端フローを正しく計算することを証明してください。
2. $G$ の最大多終端フローを正しく計算するもっと効率の良いアルゴリズムを説明してください。
Sodor 島にはたくさんの街と村があり、大規模な鉄道網によって繋がっています。ついこのあいだ致死性の伝染病 (豚インフルエンザあるいはゾンビ: 報告ははっきりしません) が Skarloey 村で何件か確認されました。Sodor 鉄道の管理者であるあなたは、いくつかの駅を封鎖して列車が止まらないようにすることで彼の住む村 Tidmouth に病気が広がらないようにしたいと考えています。ただし費用 (と広報の手間) を最小限にするために、閉鎖する駅の数は最小限にしたいとします。また閉鎖の報告をするために伝染した駅に行くことは避けたいので、Skarloey 駅を閉鎖することはできません。それからお気に入りのパブがある Tidmouth 駅を閉鎖することもできません。

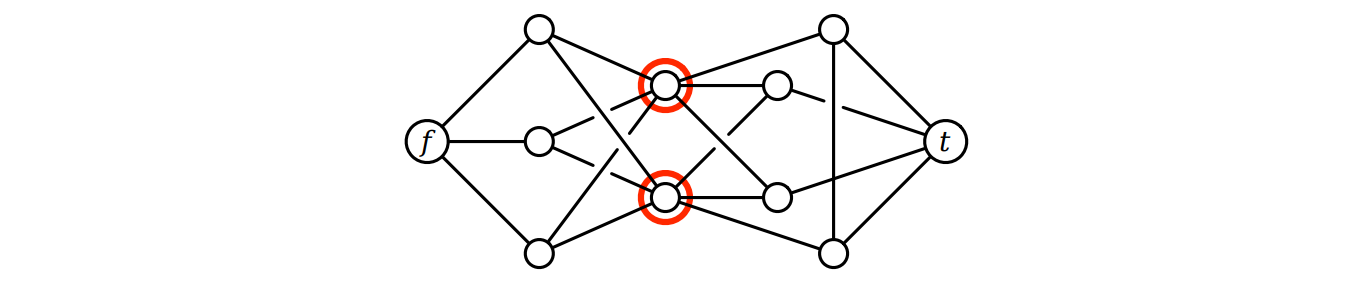
Skarloey 駅から Tidmouth 駅へ向かう鉄道路を全てブロックするために閉鎖しなければならない駅の数の最小値を求めるアルゴリズムを説明、解析してください。Sodor 鉄道のネットワークは無向グラフによって表され、頂点が駅を、辺がその間の線路を表します。Skarloey 駅と Tidmouth 駅を表す二つの特別な頂点 $s, t$ も入力に含まれます。

例えば次のグラフが入力された場合にはアルゴリズムは整数 $2$ を返します。
$n \times n$ の格子は $n^{2}$ 頂点の無向グラフとみなすことができます。$i$ 行 $j$ 列の頂点を $(i,j)$ と表記すると、$i = 1$, $i = n$, $j = 1$, $j = n$ を満たす境界上にある頂点を除いた各頂点 $(i,j)$ はちょうど四つの頂点 $(i-1, j),$ $(i+1, j),$ $(i, j-1),$ $(i,j+1)$ と隣接します。

$m$ 個の異なる頂点 $(x_{1}, y_{1}),$ $(x_{2}, y_{2}),$ $\ldots,$ $(x_{m}, y_{m})$ を終端 (terminals) とします。脱出問題 (escaping problem) とは、終端の頂点と境界上にある頂点を結ぶ $m$ 個の頂点素路が存在するかどうかを判定する問題です。

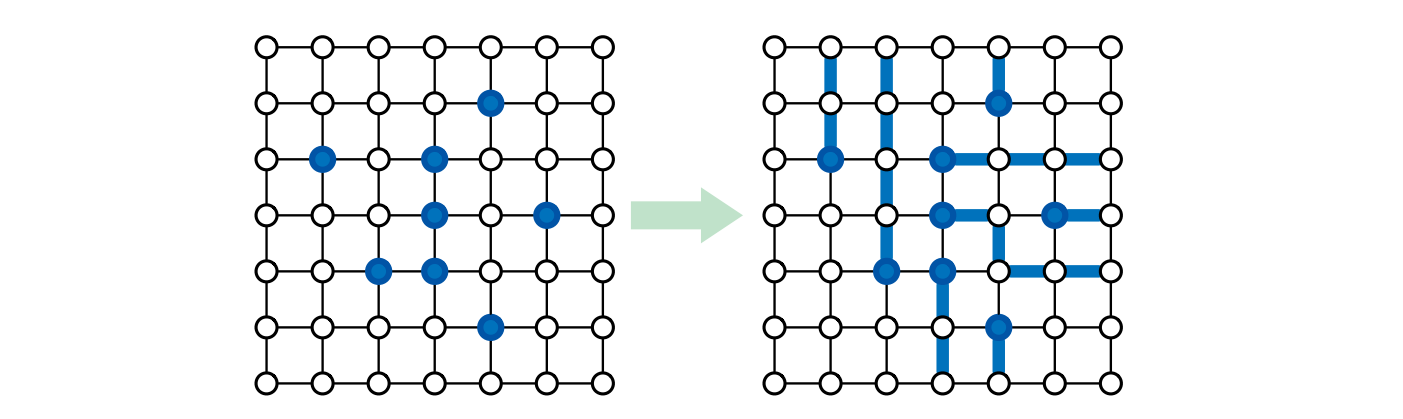図 11.8

解を持つ脱出問題のインスタンスとその解
1. 脱出問題を解く効率の良いアルゴリズムであって実行時間が次数の小さい $n$ の多項式で抑えられるものを説明、解析してください。
2. 脱出問題の入力が整数 $n$ と $m$ 個の終端頂点からなるとします。このとき $m$ を小さい値に固定すると、前問のアルゴリズムの実行時間は入力の長さに対して指数的になってしまいます！脱出問題を解くアルゴリズムで実行時間が $m$ の多項式時間であるものを説明してください。
3. ❤ 前問のアルゴリズムを変更して、脱出路が存在する場合にはその路を返すようにしてください。実行時間は $m$ の多項式のままとしてください。
SPU の情報科学科が See-Bull Center の地下にミニゴルフ場を作ることになりました！ゴルフのコースは $m$ 個の水平または垂直な線分からなる多角形であり、コースにはスタート地点とゴール地点の組が $n$ 個あります。スタートとゴールは壁にぶつからない直線で結ぶことができ、(高級なガラスでできた) 壁にボールを当てる必要はありません。また $n$ 個のスタート地点と $n$ 個のゴール地点は全て異なる点です。

残念なことに、工事に取り掛かろうとしたちょうどそのとき、コース設計者のコンピューターがクラッシュしてしまいました。システム管理者のすさまじい努力によってスタート地点とゴール地点の場所は復元できたのですが、どのスタートがどのゴールに対応しているかという情報は失われてしまいました！

スタート地点とゴール地点の直線で結ばれる対応関係を全て計算するか、そのような関係を作ることが不可能ならそうだと正しく報告するアルゴリズムを説明、解析してください。入力はコースの $m$ 個の角、$n$ 個のスタート地点、$n$ 個のゴール地点の $x, y$ 座標からなります。端点の $x,y$ 座標で表された二つの線分が交わるかどうかを定数時間で判定できるとしてください。

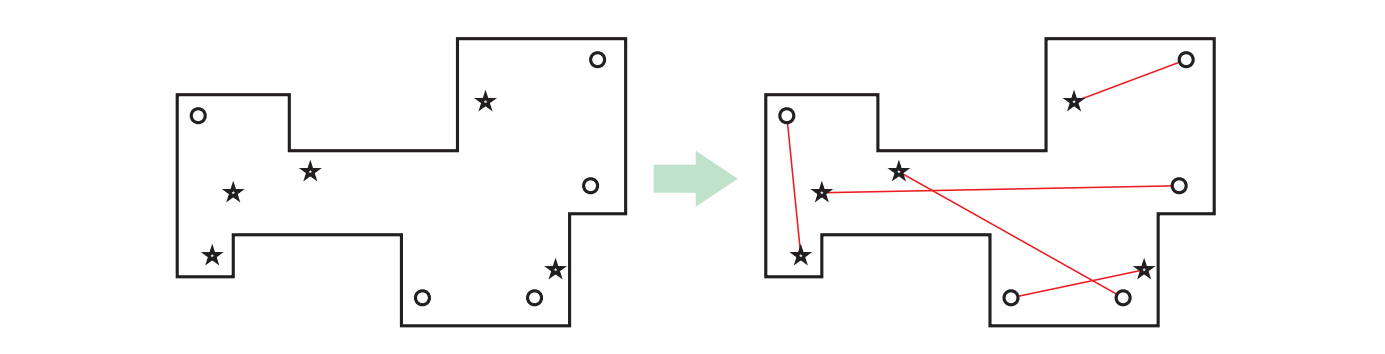$$5$ 個のスタート地点 (*) とゴール地点 (○) を持つミニゴルフコース、そして条件を満たすスタートとゴールの対応関係$

図 11.9

$5$ 個のスタート地点 (*) とゴール地点 (○) を持つミニゴルフコース、そして条件を満たすスタートとゴールの対応関係
有向グラフ $G = (V, E)$ の閉路被覆 (cycle cover) とは、$G$ に含まれる閉路の集合であって $G$ の各頂点がいずれかの閉路にちょうど一回ずつ含まれるものを言います。与えられた有向グラフの閉路被覆を見つけるか、閉路被覆が存在しないならそうだと正しく報告する効率の良いアルゴリズムを説明、解析してください。 [ヒント: 二部グラフのマッチングを使ってください！]
$n \times n$ のチェッカーボードからいくつかのマスを取り除いたものが与えられ、あなたは二マスのドミノをたくさん持っているとします。このドミノでボードを埋め尽くせるかどうかを判定するアルゴリズムを説明、解析してください。各ドミノはちょうど二マス分を埋め、全てのマスはちょうど一つのドミノによって埋められるとします。

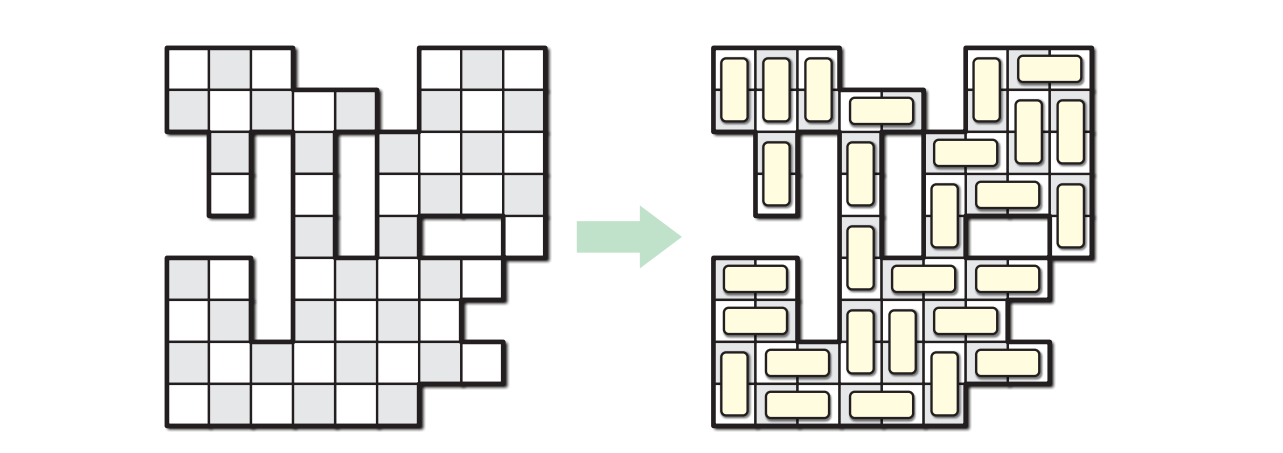図 11.10

穴の開いたチェッカーボードをドミノで埋める

入力は $\mathit{Deleted}[i..n,i..n]$ であり、$\mathit{Deleted}[i,j] = \textsc{True}$ は $i$ 行 $j$ 列目のマスが取り除かれていることを表します。出力は一つの真偽値であり、ドミノの実際の配置を計算する必要はありません。例えば上図のボードに対するアルゴリズムの答えは $\textsc{True}$ です。
マスが黒または白に塗られた $n \times n$ の格子が与えられたとします。次の条件を満たすように駒をマスに置けるかどうかを判定するアルゴリズムを説明、解析してください。
- 全ての駒は白いマスにある。
- 全ての行にはちょうど一つの駒がある。
- 全ての列にはちょうど一つの駒がある。
入力はどのマスが白いかを表す真偽値の二次元配列 $\mathit{IsWhite}[1..n, 1..n]$ であり、出力は真偽値一つです。例えば以下の格子が与えられたときのアルゴリズムの答えは $\textsc{True}$ です。

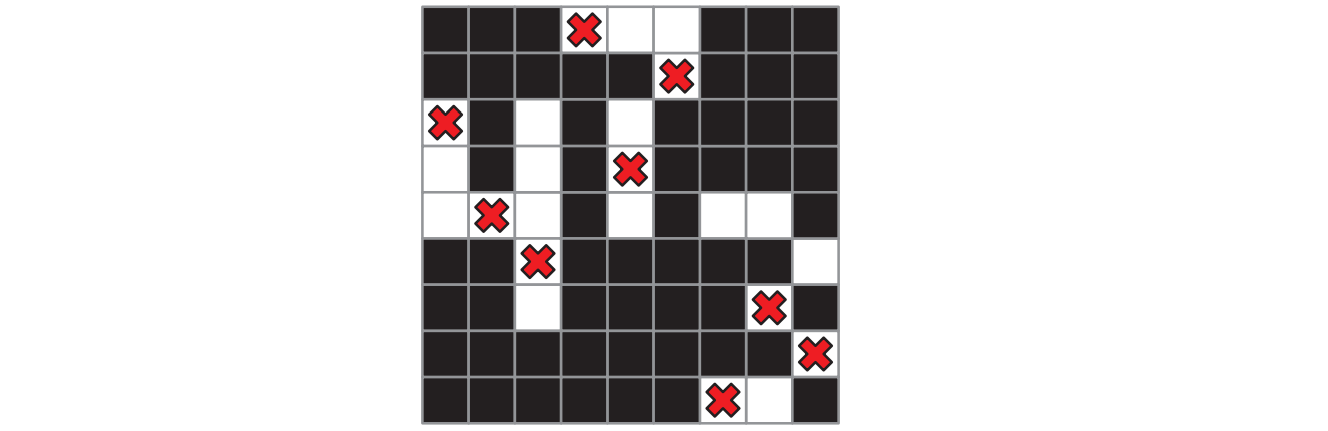図 11.11

全ての列と行に駒を置く
いくつかの箱が与えられるとします。それぞれの箱は幅、高さ、奥行きの値を持っており、全て 10 cm から 20 cm の間です。分かるとは思いますが、ある箱を回転させて幅、高さ、奥行きの全ての値を他の箱よりも小さくできる場合、小さい箱を大きい箱の中に収めることができます。ある箱が他のどの箱にも入っていないとき、その箱は見えている (visible) と言うことにします。

見えている箱の数が最小になるように箱を入れ子にするアルゴリズムを説明、解析してください。
$n \times n$ の格子が与えられ、いくつかのマスに印が付いているとします。つまり真偽値の配列 $M[1..n, 1..n]$ によって格子が表され、$(i, j)$ というマスに印が付いているときに限って $M[i,j] = \textsc{True}$ ということです。単調路 (monotone path) とは、格子の左上のマスから右下のマスへの路であって各ステップにおいて左または下にしか移動しないものを言います。この問題の目標は、印の付いた全てのマスをなるべく少ない単調路で被覆することです。

図 11.12

印の付いたマスを貪欲に単調路で被覆する
1. 被覆する印付きマスの数が最大となる単調路を計算するアルゴリズムを説明してください。
2. 簡単に思いつく貪欲なヒューリスティックとして、残っているセルを一番多く被覆する単調路を選択し、その路が被覆するマスの印を消し、再帰する、というアルゴリズムがあります。このアルゴリズムが常に最適解を計算するわけではないことを示してください。
3. 印の付いた全てのマスを被覆する単調路の集合の中で最小のものを計算する効率の良いアルゴリズムを説明、解析してください。
Sham-PooBanana 大学陸上チームの ~~マスコット~~ シンボル Factotum 男爵が不祥事を起こしたことを受けて、学部評議委員会は Gabby おじさんこと Bobo Cornelius とサイキックゴリラこと Mofo のどちらを代役にするかを選ぶ決議を行うことになりました。委員会には各学部から一人が代表として出席します。複数の学部に所属している委員もいますが、その委員が代表できるのは一つの学部だけです。例えば Blagojevich 教授が破壊学科 (Department of Corruption) と愚鈍学科 (Department of Stupidity) の委員である場合、Blagojevich 教授が愚鈍の代表として選ばれたときには破壊の代表は別の人である必要があります。また学部評議委員会に出席する助教授、准教授、教授の数は等しくなければならないと大学の規則で定められています。幸運にも学科の数は $3$ の倍数です。

ポスト Factotum Simian ~~マスコット~~ シンボル委員会を開くことができる SPU スタッフの部分集合を計算するか、どうやっても委員会を開くことはできないと正しく報告するアルゴリズムを説明、解析してください。アルゴリズムの入力はどの教授がどの学科に所属しているかを表す二部グラフであり、教授を表す頂点は教授のランク (助教授、准教授、教授) でラベル付けされています。
Sham-PooBanana 大学のコンピューターサイレンス学科 (Department of Commuter Silence) はフレキシブルなカリキュラムを持っており、卒業のための条件が複雑です。学科は $n$ 個の異なる講義を開講していて、卒業のための条件が $m$ 個あります。それぞれの条件は講義の部分集合とその中から取らなければいけない講義の数を指定します。異なる条件が指定する講義は重複することがありますが、一つの講義を条件を満たすために使ってよいのは一度だけです。

例えば $n = 5$ で $A, B, C, D, E$ という講義があり、$m = 2$ で次の条件があるとします:
- $\lbrace A,B,C \rbrace$ の中から少なくとも二つの講義を取らなければならない。
- $\lbrace C,D,E \rbrace$ の中から少なくとも二つの講義を取らなければならない。
このとき $B, C, D$ という講義を取った生徒は卒業できず、$A,B,C,D$ および $B,C,D,E$ という講義を取った生徒は卒業できます。

与えられた講義を取った生徒が卒業できるかどうかを判定するアルゴリズムを説明、解析してください。アルゴリズムの入力は $m$ 個の条件 (それぞれが講義の部分集合とその中から取るべき講義の数を指定する) と生徒の取った講義のリストです。
SPU コンピューターサイレンス学科主催第一回定期 72 時間ダンスエクスチェンジというイベントをあなたは主催しています。このイベントは金曜日、土曜日、日曜日にかけて行われ、DJ が順番に音楽のセットをかけていきます。大勢の DJ からの出演依頼が来たので、あなたの次の仕事は次の条件が満たされるように DJ を選ぶことです:
- 一日にちょうど $k$ セット、三日間で合計 $3k$ セットの音楽を流す。
- ある DJ が一度の出演で流すセットには同じジャンルの曲だけが含まれる (アンビエント、バブルガム、ダブステップ、ホラーコア、K-ポップ、クワイト、マリアッチ、ストレートアヘッドジャズ、トリップ・ホップ、ナッシュビル、カントリー、パラパラ、スカ...)。
- 同じジャンルのセットを流せるのは一日に最大でも一度だけ。
- 候補となっている DJ が流したい曲のジャンルのリストをあなたは持っている。
- イベント全体で同じ DJ が出演できるのは三回まで。
候補となっている DJ が $n$ 人いて、曲のジャンルが $g$ 個存在するとします。DJ とジャンルを $3k$ 個のセットに対応させるか、そのような対応は存在しないと正しく報告するような効率の良いアルゴリズムを説明、解析してください。
あなたはウェブサイトを管理していて、毎日決まった人がサイトを訪問しているとします。サイトの訪問者は一つ以上の人口統計学的グループに所属していて、例えばある人物は 40-50 才で、子持ちの男性で、イリノイ在住で、大学で働いていて、ブロガーで、Gilbert and Sullivan のファンである¹などの情報が分かるとします。あなたのサイトは広告によって支えられており、広告主はどの人口統計学的グループに広告を見せるべきか、および広告を一日に何回見せなければならないかを指定しています。全部で $n$ 人の訪問者と $k$ 個の人口統計学的グループと $m$ 個の広告主がいます。

以上の情報が全て与えられたとき、全ての訪問者に一日にちょうど一つだけの広告を見せることで、全ての広告主の広告を指定した回数だけ指定したグループに見せることができるかどうかを判定する効率の良いアルゴリズムを説明、解析してください。
非負実数の配列 $A[1..m][1..n]$ が与えられたとします。$A$ の各要素 $x$ を $\lceil x \rceil$ または $\lfloor x \rfloor$ に入れ替えることで、各行および各列の要素の和を変更せずに $A$ を整数行列に丸めたいとします。例えば \[ \begin{bmatrix} 1.2 & 3.4 & 2.4 \\ 3.9 & 4.0 & 2.1 \\ 7.9 & 1.6 & 0.5 \end{bmatrix} \mapsto \begin{bmatrix} 1 & 4 & 2 \\ 4 & 4 & 2 \\ 8 & 1 & 1 \end{bmatrix} \] はこの条件を満たす丸めです。
1. 条件を満たすように $A$ を丸めるか、そのような丸めは存在しないと正しく報告する効率の良いアルゴリズムを説明、解析してください。
2. 条件を満たす丸めが存在するのは各列および各行の要素の和が全て整数である場合に限ることを示してください。言い換えると、(a) のアルゴリズムが条件を満たす丸めを返さないときには、丸めが不可能なことが「明らか」であることを示してください。
3. ❤ $A$ の要素に整数が含まれないとします。条件を満たすように $A$ を丸めるか、そのような丸めは存在しないと正しく報告するさらに効率の良いアルゴリズムを説明、解析してください。満点のためにはアルゴリズムの実行時間が $O(mn)$ であることが求められます。 [ヒント: フローを使わないでください。]
アドホックネットワーク (ad-hoc network) は低消費電力のデバイスからなるネットワークであり、理論上は²自然災害で被害を受けた地域や戦場といった人が近づけない領域におけるネットワークとして機能します。アドホックネットワークのアイデアは、対象の領域に安価で単純なデバイスを (航空機から落とすなどして) 大量に撒いて、その後デバイス自身に無線ネットワークを自動的に構築させるというものです。

デバイスが通信できる距離は限られています。ここでは全てのデバイスは同一であり、任意の二つのデバイスが通信できるのはデバイス間の距離が $D$ 以下のときだけだと仮定します。

もちろんアドホックネットワークの信頼性は高いことが望ましいのですが、デバイスは安価で利用できる電力も小さいので、よく故障します。デバイスが故障の前兆を検出した場合、そのデバイスは自身の情報を通信可能な範囲にあるバックアップデバイスに送信します。各デバイス $x$ は距離 $D$ 以内にバックアップデバイスを $k$ 個持たなくてはいけないとします (この $k$ 個のデバイスを $x$ のバックアップ集合と呼ぶことにします)。またあるデバイスにネットワークが集中するのも避けたいので、一つのデバイスがあまりに多くのデバイスのバックアップ集合に含まれることもあってはいけません。

通信半径 $D$ とパラメータ $b,k$ と配列 $d[1..n,1..n]$ が与えられ、$d[i,j]$ がデバイス $i$ と $j$ の間の距離を表すとします。$n$ 個の頂点それぞれに対する大きさ $k$ のバックアップ集合であって、どの頂点も他の頂点のバックアップ集合に $b$ 回以下しか現れないものを計算するか、そのような集合は作れないと正しく報告するアルゴリズムを説明してください。
予算削減の危機にさらされた Potemkin 大学の理事は、講義が満員であるように見せかけるために、役者を雇って "生徒" として講義に出席してもらうことにしました。役者を雇うのは高くつくので、雇う役者の数は最小限にしたいと考えています。

Potemkin 大学の理事は今は亡き Sham-PooBanana 大学で培ったリーダーシップを発揮して、あなたを問題解決者として任命しました。あなたには有向非巡回グラフ $G=(V,E)$ が与えられ、頂点が講義を、辺 $i \rightarrow j$ が "生徒" が講義 $i$ に出席した後に講義 $j$ に出席できることを表します。加えて配列 $\mathit{cap}[1..V]$ も与えられ、$\mathit{cap}[i]$ が講義 $i$ に出席できる "生徒" の数の最大値を表します。全ての講義を満員にするために必要になる "生徒" の数を計算するアルゴリズムを説明、解析してください。
Quentin と Alice と Brakebills Physical Kid たちは NeitherLands を経由して Fillory まで行く旅を計画しています。NeitherLands は放棄された広大な都市であり、異世界へと通じる魔法の噴水が置かれたいくつかの広場から構成されています。隣接する広場は門でつながっており、門は Beast によって呪われています。広場の間の門は全て同じ時間に開閉し、開くのは 12:00 から 12:05 まで、1:00 から 1:05 までという風に一時間ごとに五分間だけです。この五分間の間に一つの門につき一人だけが通り抜けることができ、二人以上が門を通り抜けると Beast に気付かれてしまいます³。また閉じている門を開けようとしたり、五分間の間に二つ以上の門を通り抜けようとした人間は niffin に変えられてしまいます⁴。ただし異なる人間が異なる門を同時に通り抜けること、あるいは同じゲートを異なる時間帯に通り抜けることは可能です。

あなたは NeitherLands の地図を持っています。地図は頂点が噴水、辺が門を表す無向グラフ $G$ であり、地球と Fillory につながる噴水に印が付いています。
1. $G$ の他に正の整数 $h$ が与えられたとします。Beast に気付かれることも niffin に変えられることもなく $h$ 時間以内に ――つまり、門が $h$ 回開くまでに―― 地球から Fillory に移動できる人数の最大値を計算するアルゴリズムを説明、解析してください。実行時間は $h$ に依存するはずです。 [ヒント: 二部グラフを作ってください。]
2. ♣ ❤ (a) に対するアルゴリズムであって実行時間が $V$ と $E$ の多項式であり $h$ に依存しないものを説明、解析してください。
3. 追加のパラメータとして $h$ ではなく正の整数 $k$ が与えられたとします。Beast に気付かれることも niffin に変えられることもなく $k$ 人の人間が地球から Fillory に移動するときにかかる時間の最小値を求めるアルゴリズムを説明、解析してください。 [ヒント: (a) を使ってください。]
❤ $G = (L \sqcup R, E)$ を二部グラフとし、左側の頂点を $L = \lbrace l_{1}, l_{2}, \ldots, l_{n} \rbrace$、右側の頂点を $R = \lbrace r_{1}, r_{2}, \ldots, r_{n} \rbrace$ とします。$G$ のマッチング $M$ が非交差 (non-crossing) であるとは、任意の辺の組 $l_{i}r_{j}$ と $l_{i^{\prime}} r_{j^{\prime}}$ において $i < i^{\prime} \iff j < j^{\prime}$ なことを言います。
1. $G$ の最大非交差マッチングを見つけるアルゴリズムを説明、解析してください。 [ヒント: 実はこの問題ではフローを使いません。]
2. 非交差マッチングの集合 $\lbrace M_{1}, M_{2}, \ldots, M_{k} \rbrace$ であって $G$ の任意の辺がちょうど一つのマッチング $M_{i}$ に含まれるものの大きさの最小値を求めるアルゴリズムを説明、解析してください。 [ヒント: この問題ではフローを使います。]
❤ $G = (L \sqcup R, E)$ を二部グラフとし、左側の頂点が適当な順序で $L = \lbrace l_{1}, l_{2}, \ldots, l_{n} \rbrace$ と添え字が付いているとします。
1. $G$ のマッチング $M$ が密 (dense) であるとは、$L$ の任意の連続する頂点の少なくとも一方がマッチされていることを言います。つまり、任意の添え字 $i$ について $l_{i}$ または $l_{i+1}$ のどちらかが $M$ の辺に隣接するということです。$G$ に密なマッチングが存在するかを判定するアルゴリズムを説明してください。
2. $G$ のマッチング $M$ が疎 (sparse) であるとは、$L$ の任意の連続する頂点の少なくとも一方がマッチされていないことを言います。つまり、任意の添え字 $i$ について $l_{i}$ または $l_{i+1}$ のどちらかが $M$ の辺に隣接していないということです (例えば空のマッチングは疎です)。$G$ の疎なマッチングで最大のものを見つけるアルゴリズムを説明してください。
3. $G$ のマッチング $M$ が回文 (palindromic) であるとは、任意の添え字 $i$ について $l_{i}$ と $l_{n-i+1}$ が両方 $M$ の辺に隣接するか、そうでなければどちらも $M$ の辺に隣接しないことを言います (例えば空のマッチングは回文です)。$G$ の回文であるマッチングで最大のものを見つけるアルゴリズムを説明してください。
いずれの問題においても $R$ の頂点に関するマッチの制限はありません。
❤ 根付き木 (rooted tree) とは、有向非巡回グラフであって根と呼ばれる頂点を除いた全ての頂点 $v$ について $v$ に向かう辺が一つしか存在せず、さらに根に向かう辺が無いものを言います。同じことですが、根付き木は根の頂点と根から延びるゼロ個以上の小さな根付き木への辺からなると言うこともできます。二つの根付き木 $A, B$ が与えられたときに、ある $A$ の部分グラフと同型であり、かつある $B$ の部分グラフとも同型である根付き木のうち最大のものを計算する効率の良いアルゴリズムを説明してください。つまり、二つの根付き木の最大共通部分木を求めるアルゴリズムを説明してください。

[ヒント: 全ての頂点が $O(1)$ 個の子しか持たないとき、あるいは各頂点の子が一列に順序付けられるときにはこの問題は比較的簡単な動的計画法の問題となります。しかし次数の大きい順序の付いていない木に対しては、再帰的な小問題を効率良く組み合わせる別のテクニックが必要になります。]

I am a very good theoretical computer scientist, specifically, a geometric algorithm specialist.^[return]
実際はそうでもありませんが。^[return]
これはとても悪いです。^[return]
これはとてもとても悪いです。^[return]