線形時間で強連結成分を求める
有向グラフの強連結成分を \(O(V+E)\) 時間で計算するアルゴリズムはいくつかありますが、どれも突き詰めれば次の観察に基づいています:
命題 6.2 任意の有向グラフ \(G\) の深さ優先走査を一つ固定する。\(G\) の任意の強連結成分 \(C\) には \(C\) の中に親を含まない頂点がちょうど一つ含まれる (この頂点の親は他の強連結成分に含まれるか、そうでなければ親を持たない)。
証明 \(G\) の任意の強連結成分を \(C\) とする。適当な頂点 \(v \in C\) から \(w \in C\) への任意の路を考える。この路上の全ての頂点は \(w\) に到達でき、したがって \(C\) の全ての頂点に到達できる。対称的に、この路上の全ての頂点は \(v\) から到達でき、したがって \(C\) の全ての頂点から到達できる。よってこの路上の全ての頂点も \(C\) に属する。
\(v\) を \(C\) の中で一番早い開始時間を持つ頂点とする。\(v\) の親 \(\mathit{parent}(v)\) は \(v\) よりも早く始まっているので \(C\) に属さない。
\(w\) を \(C\) に属する \(v\) と異なる頂点とする。 \(\textsc{DFS}(v)\) が呼ばれる直前、\(C\) の全ての頂点は未処理だから、未処理の頂点だけを通る \(v\) から \(w\) への路が存在する。命題 6.1より、深さ優先森において \(w\) は \(v\) の子孫である。よって木辺だけからなる \(v\) から \(w\) への路に含まれる頂点は全て \(C\) に含まれる。特に \(\mathit{parent}(w) \in C\) である。 \(\Box\)
この命題を使えば、有向グラフ \(G\) の各強連結成分が \(G\) の深さ優先探索森の連結部分木を定義することが示せます。具体的には各強連結成分 \(C\) について、 \(C\) の中で開始時間の最も早い頂点が \(C\) の全ての頂点を子孫として持つ最も低い頂点 (\(C\) の頂点の lowest common ancestor) となります。この頂点のことをこれから \(C\) の根 (root) と呼びます。
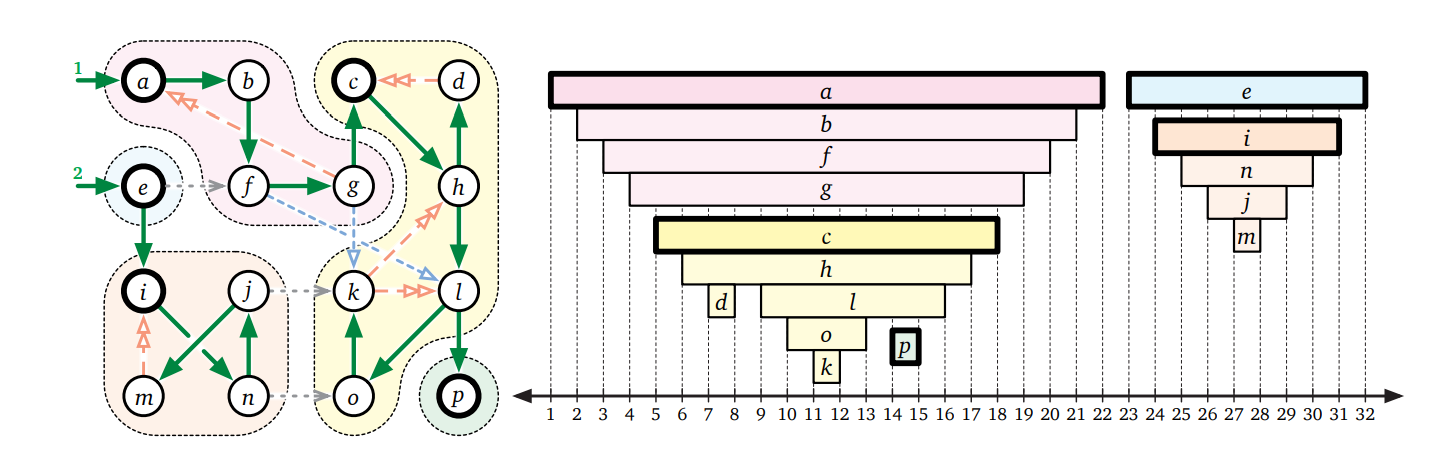
これから二つのアルゴリズムを示しますが、どちらもここに示す観察に基づいています: \(G\) の強連結成分 \(C\) であって \(\mathit{scc}(G)\) でシンクであるものを考えます。このような \(C\) をシンク成分 (sink component) と呼びます。同じことですが、\(C\) がシンク成分なのは \(C\) に含まれる頂点から到達できる頂点の集合が \(C\) と同じときです。\(G\) のシンク成分に含まれる頂点 \(v\) を (何らかの方法で) 見つけることができれば、それを繰り返すことで \(G\) の全ての強連結成分を計算できます。つまり、\(v\) を見つけ、\(v\) から到達できる頂点の集合 (シンク成分) を計算し、シンク成分をグラフから消すという処理を頂点が無くなるまで繰り返すということです。シンク成分に含まれる頂点を見つける方法が分からないので、この説明をアルゴリズムと呼ぶことはできませんが!
procedure \(\texttt{StrongComponents}\)(\(G\))
\(count \leftarrow 0\)
while \(G\) が空でない do
\(C \leftarrow \varnothing\)
\(count \leftarrow count + 1\)
\(\color{red}{v \leftarrow G}\) のシンク成分に含まれる適当な頂点 \(\quad\) ⟨⟨マジック!⟩⟩
for \(\mathit{reach}(v)\) に含まれる頂点 \(w\) do
\(\mathit{w.label} \leftarrow count\)
\(w\) を \(C\) に加える
\(C\) と \(C\) に向かう辺を \(G\) から削除する
Kosaraju と Sharir のアルゴリズム
一目見ただけでは、グラフのシンク成分に含まれる頂点を素早く見つけるというのはとても難しく思えます。しかし、グラフのソース成分 ――\(\mathit{scc}(G)\) におけるソースに対応する \(G\) の強連結成分―― に含まれる頂点を見つけるという正反対の問題なら、実は深さ優先探索を使ってとても簡単に解くことができます。
命題 6.3 \(G\) の帰りがけ順序で最後に来る頂点は \(G\) のソース成分に含まれる。
証明 適当な \(G\) の深さ優先走査を固定し、その帰りがけ順序で最後に来る頂点を \(v\) とする。このとき \(\textsc{DFS}(v)\) という呼び出しはラッパーアルゴリズム \(\textsc{DFSAll}\) が行う最後の \(\textsc{DFS}\) 関数の呼び出しである。さらに \(v\) は深さ優先全域木森の根だから、\(\mathit{v.pre} < \mathit{x.post}\) を満たす任意の頂点 \(x\) は \(v\) の子孫である。そして、\(v\) は自身が属する強連結成分 \(C\) の根である。
背理法を使って、\(x \notin C\) かつ \(y \in C\) である辺 \(x \rightarrow y\) が存在しないことを示す。\(x \notin C\) かつ \(y \in C\) である辺 \(x \rightarrow y\) が存在すると仮定する。このとき \(x\) は \(y\) に到達でき、かつ \(y\) は \(v\) に到達できるので、\(x\) は \(v\) に到達できる。\(v\) は \(C\) の根であることから \(y\) は \(v\) の子孫であり、よって \(\mathit{v.pre} < \mathit{y.pre}\) である。加えて辺 \(x \rightarrow y\) の存在より \(\mathit{y.pre} < \mathit{x.post}\) が言えるので、\(\mathit{v.pre} < \mathit{x.post}\) が分かる。したがって \(x\) は \(v\) の子孫となるが、このとき \(v\) は (木辺をたどって) \(x\) に到達できるので \(x \in C\) であり、 \(x \notin C\) という仮定と矛盾する。 \(\Box\)
任意の有向グラフ \(G\) に対して \(\mathit{rev}(\mathit{scc}(G)) = \mathit{scc}(\mathit{rev}(G))\) となることは簡単に確認できる (ヒント、ヒント) ので、 \(\mathit{rev}(G)\) の帰りがけ順序で最後の頂点が元のグラフ \(G\) のシンク成分に含まれます。したがって、\(\mathit{rev}(G)\) の帰りがけ順に頂点をたどるラッパー関数を使って二回目の走査を行えば、\(\textsc{DFS}\) の各呼び出しはちょうど一つの \(G\) の強連結成分を訪れます1。
全てまとめると、次に示すアルゴリズムを得ます。このアルゴリズムは任意の有向グラフの強連結成分の数を数え、頂点を強連結成分の番号でラベル付けするという処理を \(O(V+E)\) 時間で行います。このアルゴリズムは 1978 年に Rao Kosaraju (ラオ・コサラジュ) によって発見され (しかし公表はされず)、その後 1981 年2に Micha Sharir (ミカ・シャリア) によって独立に発見されました。Kosaraju-Sharir のアルゴリズムは二つのフェーズからなります。一つ目のフェーズは \(\mathit{rev}(G)\) に対する深さ優先探索であり、探索が終わった頂点を順にスタックに積んでいきます。二つ目のフェーズは元のグラフ \(G\) に対する何か優先探索であり、この探索はフェーズ 1 でスタックに積んだ頂点をポップしながら行います。このアルゴリズムは (二回目の深さ優先探索で) 各頂点を強連結成分の根でラベル付けします。
procedure \(\texttt{KosarajuSharir}\)(\(G\))
\(S \leftarrow\) 空のスタック
for 頂点 \(v\) do
\(v\) の印を消す
\(\mathit{v.root} \leftarrow \textsc{None}\)
⟨⟨フェーズ 1: \(\mathit{rev}(G)\) の帰りがけ順にプッシュする⟩⟩
for 頂点 \(v\) do
if \(v\) に印が付いていない then
\(\texttt{PushPostRevDFS}\)(\(v, S\))
⟨⟨フェーズ 2: スタックの順番に \(G\) をもう一度 \(\textsc{DFS}\) する⟩⟩
while \(S\) が空でない do
\(\color{#2D2F91}{v \leftarrow \textsc{Pop}(S)}\)
if \(\mathit{v.root} = \textsc{None}\) then
\(\texttt{LabelOneDFS}\)(\(v, v\))
procedure \(\texttt{PushPostRevDFS}\)(\(v, S\))
\(v\) に印をつける
for \(u \rightarrow v\) の形をした辺 ⟨⟨逆!⟩⟩ do
if \(u\) に印が付いていない then
\(\texttt{PushPostRevDFS}\)(\(u, S\))
\(\color{#2D2F91}{\textsc{Push}(v, S)}\)
procedure \(\texttt{LabelOneDFS}\)(\(v, r\))
\(\mathit{v.root} \leftarrow r\)
for \(v \rightarrow w\) の形をした辺 do
if \(\mathit{w.root} = \textsc{None}\) then
\(\texttt{LabelOneDFS}\)(\(w, r\))
Kosaraju-Sharir のアルゴリズムをこれまで使ってきた例のグラフに適用した様子を次の図に示します。このアルゴリズムをほんの少し変更すれば、強連結成分グラフ \(\mathit{scc}(G)\) を \(O(V+E)\) 時間で計算するアルゴリズムを得ることができます。
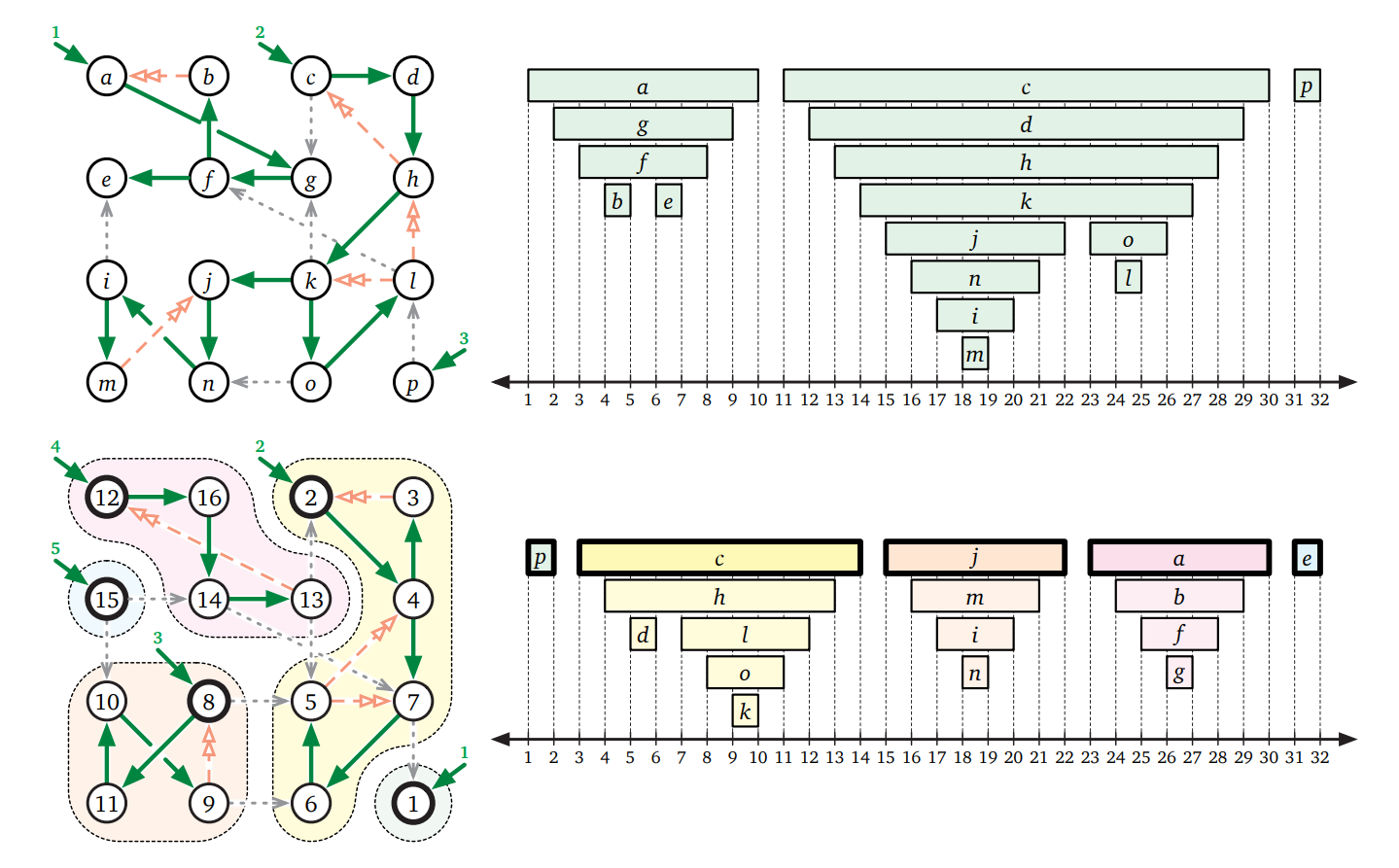
❤ Tarjan のアルゴリズム
1972 年3に Bob Tarjan (ボブ・タージャン) によって発表された強連結成分を計算する線形時間アルゴリズムは、Kosaraju-Sharir のアルゴリズムよりも早く発見されていますが、はるかに細かなテクニックを使います。直感的に説明すると、Tarjan のアルゴリズムは \(G\) のソース成分を見つけ、"削除" し、"再帰的に" 残りの強連結成分を見つけます。そして重要なのが、この計算全体が一回の深さ優先探索で行われる点です。
有向グラフ \(G\) の適当な深さ優先探索を固定します。各頂点 \(v\) について、\(v\) から木辺のみをたどって到達できる頂点からさらに一つ以下の木辺でない辺をたどって到達できる頂点の開始時間の中で最速のものを \(\pmb{\mathit{low}(v)}\) で表すことにします。この定義から自明に分かることとして、\(\mathit{low}(v) \leq \mathit{v.pre}\) です。なぜなら \(v\) はゼロ個の木辺とゼロ個の木辺でない辺をたどることで \(v\) から到達できる頂点だからです。Tarjan はこの \(\mathit{low}\) 関数を使ったシンク成分の特徴付けを発見しました。
命題 6.4 頂点 \(v\) が \(G\) のシンク成分の根であることは、\(\mathit{low}(v) = \mathit{v.pre}\) かつ \(v\) の全ての真の子孫 \(w\) について \(\mathit{low}(w) < \mathit{w.pre}\) であることと同値である。
証明 まず \(\mathit{low}(v) = \mathit{v.pre}\) が成り立つ \(v\) を選ぶ。\(\mathit{low}(v) = \mathit{v.pre}\) より、\(w\) を \(v\) の任意の子孫とすると、辺 \(w \rightarrow x\) であって \(\mathit{x.pre} < \mathit{v.pre}\) が成り立つものは存在しない。一方で何か優先探索の定義より \(\mathit{y.pre} > \mathit{v.post}\) を満たす頂点 \(y\) には \(v\) から到達できない。よって \(v\) から到達できるのは \(v\) の深さ優先探索森における子孫だけであり、\(v\) の子孫が到達できるのは \(v\) の子孫だけと分かる。加えて \(v\) に親が存在したとしても到達できないので、\(v\) は強連結成分の根である。
これに加えて \(v\) の全ての真の子孫 \(w\) に対して \(\mathit{low}(w) < \mathit{w.pre}\) が成り立つとする。このとき、全ての \(v\) の子孫 \(w\) に対して、\(w\) が到達できる (同じく \(v\) の子孫である) 頂点 \(x\) で \(\mathit{x.pre} < \mathit{w.pre}\) を満たすものが存在する。よって帰納法により \(v\) の任意の子孫は \(v\) に到達できることが分かる。したがって \(v\) の子孫は \(v\) が根であるような強連結成分 \(C\) を構成する。さらに \(v\) からは \(C\) でない頂点に到達できないことから、\(C\) はシンク成分である。
逆に \(v\) がシンク成分 \(C\) の根であると仮定する。このとき \(v\) が \(w\) に到達できることは \(w \in C\) と同値である。\(v\) は \(v\) の子孫全てに到達でき、\(C\) に含まれる頂点は \(v\) の子孫であるから、\(v\) の子孫がちょうど \(C\) となる。もしある \(w \in C\) に対して \(\mathit{low}(w) = \mathit{w.pre}\) ならば \(w\) が \(C\) のもう一つの根となるが、そんなことはあり得ない。 \(\Box\)
頂点 \(w\) に対する \(\mathit{low}(w)\) の計算は深さ優先探索を使って素直に行えます:
procedure \(\texttt{FindLow}\)(\(G\))
\(\mathit{clock} \leftarrow 0\)
for 頂点 \(v\) do
\(v\) の印を消す
for 頂点 \(v\) do
if \(v\) に印が付いていない then
\(\texttt{FindLowDFS}\)(\(v\))
procedure \(\texttt{FindLowDFS}\)(\(v\))
\(v\) に印をつける
\(\mathit{clock} \leftarrow \mathit{clock} + 1\)
\(\mathit{v.pre} \leftarrow \mathit{clock}\)
\(\mathit{v.low} \leftarrow \mathit{v.pre}\)
for \(v \rightarrow w\) の形をした辺 do
if \(w\) に印が付いていない then
\(\texttt{FindLowDFS}\)(\(w\))
\(\mathit{v.low} \leftarrow \min \lbrace \mathit{v.low},\ \mathit{w.low} \rbrace\)
else
\(\mathit{v.low} \leftarrow \min \lbrace \mathit{v.low},\ \mathit{w.pre} \rbrace\)
命題 6.4から、\(\textsc{FindLow}\) 実行した後にグラフ全体に対する何か優先探索を行うことで全てのシンク成分の根を \(O(V + E)\) 時間で計算できます。その後シンク成分に印をつけて削除するのは (根から始まる何か優先探索で) \(O(V+E)\) 時間で行えます。以上の処理を再帰的に行えば強連結成分を計算できますが、残念ながらこのアルゴリズムでは反復ごとに頂点を一つしか取り除けない可能性があります。その場合反復が最大で \(V\) 回行われるため、このナイーブなアルゴリズムの実行時間は \(O(VE)\) となってしまいます。
この戦略を高速化するために、Tarjan のアルゴリズムは頂点のスタックを (再帰スタックとは別に) 管理します。新しい頂点の探索を始めるときに頂点をスタックにプッシュしていき、頂点 \(v\) の探索が終わるたびに \(\mathit{v.low}\) と \(\mathit{v.pre}\) を比較します。初めて \(\mathit{v.low} = \mathit{v.pre}\) となったとき、次の三つの条件が成り立ちます:
- \(v\) はシンク成分 \(C\) の根である。
- \(C\) に含まれる頂点はスタックの頂上から連続して積まれている。
- スタックの一番深くに積まれている \(C\) の頂点は \(v\) である。
よってスタックを \(v\) が出てくるまでポップすれば、この時点で \(C\) の頂点を特定できます。
特定した \(C\) の頂点をグラフから削除して残りのグラフの強連結成分を再帰的に計算することもできますが、こうすると \(v\) から始まる同じ探索をもう一度行うことになるので無駄があります。その代わり、\(C\) の各頂点に強連結成分の根が \(v\) であることを示すラベルを付け、それらの頂点を以降の深さ優先探索で無視するようにします。きちんと言うと、探索をこう改変することで、\(\mathit{low}(v)\) の定義が「\(v\) から木辺のみをたどって到達できる頂点からさらに一つ以下の木辺でない辺をたどって到達できる \(\pmb{v}\) と同じ強連結成分に属する頂点の開始時間の中で最速のもの」となります。ただしアルゴリズムの正しさを証明するには、ラベルの付いた頂点を無視したときと実際にそれらの頂点を削除したときのアルゴリズムの振る舞いが同じことを示すだけで済みます。
これでようやく Tarjan のアルゴリズムを示せます。\(\textsc{FindLow}\) からの変更を赤字で示します。アルゴリズムは二つの部分に分かれます。一つは各頂点が一回ずつスタック \(S\) にプッシュおよびポップされる部分で、実行時間は \(O(V)\) です。残りは標準的な深さ優先探索で、実行時間は \(O(V+E)\) です。したがって、アルゴリズム全体の実行時間は \(\pmb{O(V+E)}\) となります。
procedure \(\texttt{Tarjan}\)(\(G\))
\(\mathit{clock} \leftarrow 0\)
\(S \leftarrow\) 新しい空のスタック
for 頂点 \(v\) do
\(v\) の印を消す
\(\mathit{v.root} \leftarrow \textsc{None}\)
for 頂点 \(v\) do
if \(v\) に印が付いていない then
\(\texttt{TarjanDFS}\)(\(v\))
procedure \(\texttt{TarjanDFS}\)(\(v\))
\(v\) に印をつける
\(\mathit{clock} \leftarrow \mathit{clock} + 1\)
\(\mathit{v.pre} \leftarrow \mathit{clock}\)
\(\mathit{v.low} \leftarrow \mathit{v.pre}\)
\(\color{red}{\textsc{Push}(S, v)}\)
for \(v \rightarrow w\) の形をした辺 do
if \(w\) に印が付いていない then
\(\texttt{FindLowDFS}\)(\(w\))
\(\mathit{v.low} \leftarrow \min \lbrace \mathit{v.low},\ \mathit{w.low} \rbrace\)
else if \(\color{red}{\mathit{w.root} = \textsc{None}}\) then
\(\mathit{v.low} \leftarrow \min \lbrace \mathit{v.low},\ \mathit{w.pre} \rbrace\)
if \(\color{red}{\mathit{v.low} = \mathit{v.pre}}\) then
\(\color{red}{w \leftarrow \textsc{Pop(S)}}\)
while \(\color{red}{w \neq v}\) do
\(\color{red}{\mathit{w.root} \leftarrow v}\)
\(\color{red}{w \leftarrow \textsc{Pop}(S)}\)
\(\color{red}{\mathit{w.root} \leftarrow v}\)
-
もう一度書いておきます: \(\mathit{rev}(G)\) の帰りがけ順の逆順は \(G\) の帰りがけ順と等しくはありません。[return]
-
同じアルゴリズムが Kosaraju よりも前にロシアの文献に登場するという噂がありますが、この噂を裏付ける信頼できるソースを見つけることができませんでした。[return]
-
伝説によると、Kosaraju はアルゴリズムの講義中にこのアルゴリズム発見したと言われています。彼は Tarjan のアルゴリズムを説明することになっていたのですが、ノートを忘れてしまったのでその場で埋め合わせをしなければならなかったそうです。この話について私が唯一驚くのは、誰も Sharir と Tarjan については同じことを言わない点です。[return]