イントロダクション

アルゴリズムとは何か？

アルゴリズムとは、明示的で、精確で、曖昧さを持たない、機械で実行できる簡単な命令を並べたものです。アルゴリズムは通常何らかの目的を念頭において作られます。例えば次のアルゴリズムは、"99 Bottles of Beer on the Wall" という歌の 99 の部分を任意の値にした歌を歌います:

アルゴリズム恐怖症の古典学者は「アルゴリズム (algorithm)」という語がギリシャ語の「数 (arithmos, \(\acute{\alpha} \varrho \iota \theta \acute{o} \varsigma\))」と「痛み (algos, \(\ddot{\alpha} \lambda \gamma o \varsigma\))」の派生語であると思うかもしれませんが、そうではありません。「アルゴリズム」 という語は九世紀のペルシャ人科学者 Abū 'Abdallāh Muḥammad ibn Mūsā al-Khwārizmī¹ (アブー・アブドゥッラー・ムハンマド・イブン・ムーサー・アル＝フワーリズミー) に由来します。

Al-Khwārizmī は Al-kitāb al-mukhtaṣar fī ḥisāb al-ğabr wa'l-muqābala (アル・キターブ・アル・ムクタザール・フィ・ヒサブ・アルジャバ・ヴァルムカバラ) という文献²の著者としてもっともよく知られています (現代の「代数 (algebra)」という語はこの文献に由来します)。また Al-Khwārizmī はこれとは別の文献で、数世紀前のインドで発明された、数の処理と筆記のための革新的な十進法 ――ある量が存在しないことを示す小さな円 ṣifr を使う方法―― を説明しています。この文献で数字や石を使って説明される様々な手続きは後に英語で algorism あるいは augrym (アラビア式記数法) と呼ばれるようになり、その数字には cipher (アラビア数字) という名前が付きました。

位取り記数法と Al-Khwārizmī の著作は両方ともヨーロッパの学者の一部には知られていましたが、この "ヒンズー・アラビア式" 記数法がヨーロッパ中に広まったのは中世のイタリア人数学者であり商人でもあった Leonardo of Pisa (ピサのレオナルド) によるところが大きいです。彼は Fibonacci (フィボナッチ) という名の方がよく知られているでしょう。Fibbonacci の 1202 年の著作 Liber Abaci³ などによって、十三世紀のヨーロッパにおける計算⁴の手段は表 (アバカス) と指⁵から手書きの数字に移っていきました。なお移行が進んだ理由は数字が使いやすかったり学びやすかったりしたためではなく、手書きの数字を使うと会計の追跡が可能なためです。アラビア数字が西洋で広く使われるようになるのは活版印刷が発明されてからであり、本当に世界中至る所で使われるようになるのはようやく十九世紀になって安い紙が大量に手に入るようになってからです。

やがて algorism という語はギリシャ語 arithmos の派生語だと (そしておそらくは前に触れた algos の派生語だとも⁶) 誤解され、現代的な algorithm という表記になりました。こういった歴史から、ごく最近まで algorithm という語はアラビア数字を使った位取り法という技法だけを意味していました。この数字を使った手続きをミスなく高速に実行できる人は algorist とか computator あるいは computer と呼ばれました。

掛け算

アルゴリズムが正式な学術研究の対象となってまだ数十年しか経っていませんが、人類は文明が始まった頃からアルゴリズムを使ってきました。計算手順の詳細な説明は人類が言語を書き留めた最も古い例の一つです。それは Fibonacci や al-Khwārizmī よりもずっと前のことで、彼らが広めた位取り記数法よりもさらに前のことです。

格子掛け算

少なくとも多くのアメリカ人の学生にとって、大きな整数を掛け算する方法として一番なじみ深いのは格子掛け算 (lattice multiplication) です。このアルゴリズムは Fibonacci の著作 Liber Abaci によって広まりました。

Fibonacci はこのアルゴリズムを al-Khwārizmī などのアラビアの文献から得ており、al-Khwārizmī などのアラビアの数学者が学んだのは七世紀に Brahmagupta (ブラフマグプタ) によって書かれた Brāhmasphuṭasiddhānta (ブラフマースプタシッダーンタ) をはじめとするインドの文献です。さらにインド人の数学者が中国の文献から学んでいたという可能性もあります。

格子アルゴリズムを説明した現存する最古の資料は、三世紀から五世紀の間に中国で書かれた『孫子算経』、および起源 500 年ごろに Eutocius of Ascalon (アシュロンのユートキアス) によって書かれた Archimedes (アルキメデス) の『円の計測』に対する注釈です。しかしそれよりもずっと以前から使われていたことを示す資料があります。Eutocius は格子アルゴリズムの考案者として紀元前 300 年ごろの人物 Apollonius of Perga (ペルガのアポロニウス) とその著作 \(\Omega \kappa \upsilon \tau \acute{o} \kappa \iota o \nu\)⁷ (オキトキオン) に言及しています (この文献は現存しません)。またシュメール人は紀元前 2600 年ごろには既に乗算表を粘土板に記録しており、格子アルゴリズムが使われていた可能性があります⁸。

格子アルゴリズムは入力の数が桁ごとに数字を並べた文字列で表されることを仮定します。ここでは 10 進法を使いますが、格子アルゴリズムは簡単に任意の底に一般化できます。表記を簡単にするために、入力が \(X[0..m-1]\) と \(Y[0..n-1]\) という配列の組であり⁹、それぞれ \[ x = \sum_{i=0}^{m-1} X[i] \cdot 10^{i}, \quad y = \sum_{j=0}^{n-1} Y[j] \cdot 10^{j} \] という数を表すとします。そして出力も同じように \(Z[0..m+n-1]\) であり、 \[ z = x \cdot y = \sum_{k=0}^{m+n-1} Z[k] \cdot 10^{k} \] という積を表すとします。

格子アルゴリズムは足し算と一桁の掛け算を基本演算として使います。足し算は一段の for ループで計算し、一桁の掛け算にはルックアップテーブルを使うことが多いです。ルックアップテーブルを使うとはつまり、掛け算の値を事前に粘土板に刻んだり、木簡や竹簡あるいは紙に書いたり、読み込み専用のメモリに書き込んだり、計算者 (computator) が記憶したりするということです。

格子掛け算のアルゴリズムは次の式で要約できます: \[ x \cdot y = \sum_{i=0}^{m-1} \sum_{j=0}^{n-1}(X[i] \cdot Y[j] \cdot 10^{i+j}) \] 異なる格子アルゴリズムは部分積 \(X[i] \cdot Y[j] \cdot 10^{i+j}\) を異なる順番で計算したり、和の計算に異なる方法を使ったりします。例えば Liber Abaci で Fibbonacci が説明したのは \(mn\) 個の部分積を小さい順に計算する方法であり、次の疑似コードで表されます:

Fibonacci のアルゴリズムを人間が実行するときには、部分積を (「タブロー」とか「格子」とか呼ばれる) 二次元の表に記録し、対角線に沿って繰り上りを考えながら足して最終的な答えを計算するという方法がよく使われます。この様子を図 0.1の右側に示します。この図の左側に示すのは、一方の数 (掛けられる数) をもう一方の数 (掛ける数) の各桁で掛け、その結果を縦に並べて書いてからまとめて足すという方法です。これは現代のアメリカの小学校で教えられている方法であり、Eutocius によっても説明されています。ただし図 0.2に示すように、Eutocius の時代には数を左から右に書きました。

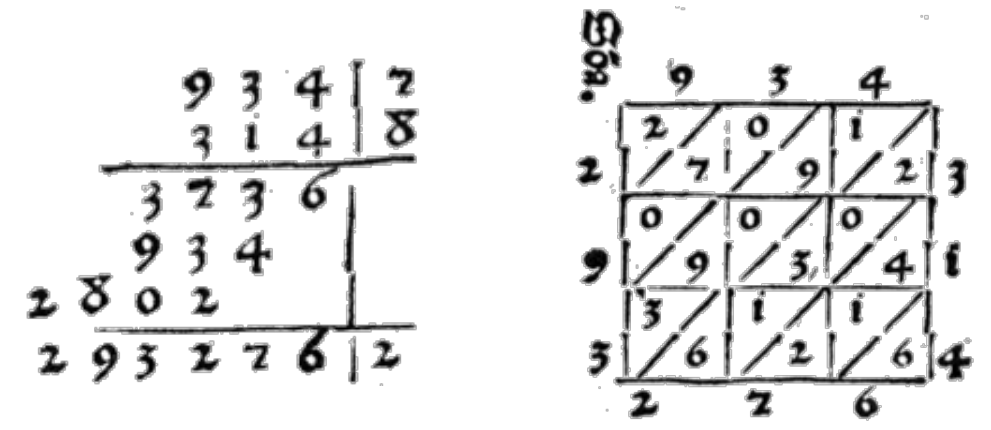
これら二つのアルゴリズムは両方とも (いくつかの別種と共に) 1458 年の作者不詳の教本 L'Arte dell'Abbaco で説明され、並んで図も載っています。この本は Treviso Arithmetic としても知られており、西洋で最初の印刷された数学書です。

こういった格子アルゴリズムの変種 ――Sunzi, al-Khwārizmī, Fibonacci, L'Arte dell'Abbaco および他のたくさんの資料で見られる似たようなアルゴリズム―― は全て、任意の \(m\) 桁の数と \(n\) 桁の数の積を \(O(mn)\) 時間で計算し、実行時間は一桁の掛け算の数によって支配されます。

Duplation と Mediation

格子アルゴリズムは直接的な記録が残っている最古の乗算アルゴリズムではありません。これよりもさらに古く、そして明らかにより単純なアルゴリズムが存在します。それは "ロシア農民の掛け算" または "エチオピア農民の掛け算"、あるいは単純に農民の掛け算 (peasant multiplication) と呼ばれるアルゴリズムであり、このアルゴリズムは位取り記数法を必要としません。

エジプト人書記官 Ahmes (アーメス) がこのアルゴリズムの一種をリンド数学パピルスと呼ばれる文書に書き写したのは紀元前 1650 年前後のことです。その中で彼は、このアルゴリズムが当時約 350 年前から知られていたと記しています¹²。東欧の小学校では二十世紀の終わりごろまでこのアルゴリズムが実際に教えられていました。また整数乗算がハードウェアで実装されていない初期のデジタルコンピューターで乗算の計算に使われていたのもこのアルゴリズムです。

農民の掛け算アルゴリズムは任意の数の掛け算という難しいタスクを 4 つの簡単な操作の列に置き換えます。つまり (1) パリティ (奇数か偶数か) の検査、(2) 足し算、(3) duplation (数を2倍する)、(4) mediation (数を2で割って、小数部分を切り捨てる) です。疑似コードを次に示します:

このアルゴリズムの正しさは、非負整数 \(x\) と \(y\) に関する次の再帰的な等式と帰納法から従います: \[ x \times y = \begin{cases} 0 & \text{if } x = 0 \\ \lfloor x / 2 \rfloor \times (y + y) & \text{if } x \text{ が偶数} \\ \lfloor x / 2 \rfloor \times (y + y) + y & \text{if } x \text{ が奇数} \\ \end{cases} \] この再帰方程式が農民の掛け算アルゴリズムそのものであるとも言えるでしょう。疑似コードのループに惑わされないでください: このアルゴリズムは本質的に再帰的です！

上述の通り、\(\textsc{PeasantMultiply}\) はパリティ検査と足し算と mediation 演算を \(O(\log x)\) 回行います。ここで \(x > y\) のときに \(x\) と \(y\) を取り換えることで、この回数を \(O(\log \min\lbrace x, y \rbrace)\) にできます。さらに底が大きすぎない位取り記数法 (二進法、十進法、バビロニアの六十進法、エジプトの十二進法、ローマ数字、中国の算木) を使って数を表していると仮定すれば、それぞれの基本演算は最大 \(O(\log (xy)) =\) \(O(\log \max\lbrace x, y \rbrace)\) 回の一桁の演算を必要とします。よってアルゴリズム全体の実行時間は \(O(\log \min \lbrace x, y \rbrace \cdot \log \max\lbrace x, y \rbrace) =\) \(O(\log x \cdot \log y)\) となります。

これを言い換えると、農民の掛け算アルゴリズムを使って \(m\) 桁の数と \(n\) 桁の数の積を計算するのにかかる時間は、定数を無視すれば \(O(mn)\) であり、格子アルゴリズムと同じであるということです。農民の掛け算アルゴリズムの実行には紙上での処理が (定数倍の範囲で！) より多く必要になりますが、必要となる基本演算 (パリティ検査、足し算、duplation、mediation) は人間にとって明らかにより簡単です。また二進法表記を使った場合には、二つのアルゴリズムは全く同じ操作となります。

コンパスと定規

古典ギリシャの幾何学者は数 (正確には大きさ) を対応する長さを持つ線分と同一視していました。彼らが線分を作成するときに使ったのは、測量技師や建築家などの職人によって既に数世紀に渡って使われていた単純な工作機械 ――コンパスと定規―― です。当時の学者は複雑な幾何学図形の作図をコンパスと定規だけを使った以下の基本処理に分解しました。この処理は一つ以上の固定された参照点から始まります。

• 既知の異なる二点の間に (唯一の) 直線を引く。
• 既知の点を中心とし、別の既知の点を通る (唯一の) 円を描く。
• 二つの直線の交点を (存在すれば) 得る。
• 円と直線の交点を (存在すれば) 得る。
• 二つの円の交点を (存在すれば) 得る。

ギリシャで幾何学を学ぶ学生が実際に作図を行うときには、ほとんどの場合アバカス (\(\ddot{\alpha} \beta \alpha \xi\)) というちりや砂に覆われたテーブルが使われました¹³。エジプトの測量技師もロープを使って直線と円を書くことでギリシャ人と同様の作図をギリシャ人より数世紀前に行っていました¹⁴。しかし Euclid を含むギリシャ人幾何学者が違っていたのが、コンパスと定規による作図を正確な数学的抽象概念とみなした点です ――点は理想的な点であり、直線は理想的な直線であり、円は理想的な円である、というように。

約 2500 年前に Euclid が『原論』で説明したアルゴリズムを次に示します。このアルゴリズムは二つの大きさを掛けるか割るかします: 入力は既知の点 \(A, B, C, D\) であり、出力として \(|AZ| = |AC||AD|/|AB|\) となる点 \(Z\) を作図します。 \(|AB|\) を単位長とすれば、このアルゴリズムで \(|AC|\) と \(|AD|\) の積を計算できます。

Euclid が \(\textsc{RightAngle}\) という新しい基本処理をサブルーチン (と現代のプログラマーが呼ぶであろうもの) として最初に定義している点に注目してください。このアルゴリズムの正しさは三角形 \(ACE\) と \(AZF\) が相似なことから従います。なおアルゴリズムのメイン処理の 2, 3 行目は円と直線の交点を求めているにもかかわらず二つの交点のどちらを選択するのかを示しておらず曖昧ですが、交点 \(E\) と \(F\) としてどちらを選んでもこのアルゴリズムは正しく動きます。

⟨⟨\(P\) を通り \(l\) に垂直な直線を作図する⟩⟩

procedure \(\texttt{RightAngle}\)(\(l, P\))

点 \(A \in l\) を選ぶ

\(A, B \leftarrow\)\(\texttt{Intersect}\)(\(\texttt{Circle}\)(\(P, A\)),\(\,\)\(l\))

\(C, D \leftarrow\)\(\texttt{Intersect}\)(\(\texttt{Circle}\)(\(A, B\)),\(\,\)\(\texttt{Circle}\)(\(B, A\)))

return \(\texttt{Line}\)(\(C, D\))

\(\ \)

⟨⟨\(|AZ| = |AC||AD|/|AB|\) を満たす点 \(Z\) を作図する⟩⟩

procedure \(\texttt{MultiplyOrDivide}\)(\(A, B, C, D\))

\(\alpha \leftarrow \)\(\texttt{RightAngle}\)(\(\texttt{Line}\)(\(A, C\)), \(A\))

\(E \leftarrow\)\(\texttt{Intersect}\)(\(\texttt{Circle}\)(\(A, B\)), \(\alpha\))

\(F \leftarrow\)\(\texttt{Intersect}\)(\(\texttt{Circle}\)(\(A, D\)), \(\alpha\))

\(\beta \leftarrow \)\(\texttt{RightAngle}\)(\(\texttt{Line}\)(\(E, C\)), \(F\))

\(\gamma \leftarrow \)\(\texttt{RightAngle}\)(\(\beta, F\))

return \(\texttt{Intersect}\)(\(\gamma, {}\)\(\texttt{Line}\)(\(A,C\)))

図 0.4

コンパスと定規を使った掛け算

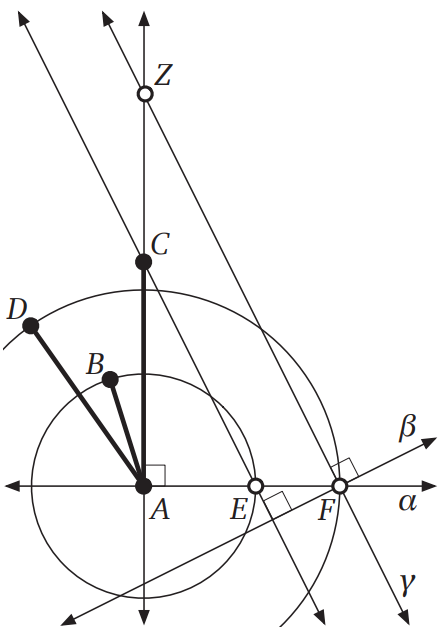
Euclid のアルゴリズムは、二つの大きさ (長さ) の掛け算をコンパスと定規を使った一連の基本処理に帰着させます。この処理をデジタルコンピューターで正確に行うのは困難ですが、Euclid のアルゴリズムはデジタルコンピューターで実行するように設計されたわけではありません。そうではなく、このアルゴリズムはプラトンの理想的なコンパスと定規を使って基本処理を完璧な正確さで実行する、理想的な幾何学のために設計されています。理想的な幾何学者は定義により基本処理を定数時間で実行するので、この計算モデルにおける \(\textsc{MultiplyOrDivide}\) の実行時間は \(O(1)\) です！

議会の議席配分

現実世界のアルゴリズムの例をもう一つ示しましょう。このアルゴリズムは政治的に非常に重要です。アメリカ合衆国憲法第 1 条第 2 節は次のことを定めています:

下院議員と直接税はこの連邦に加入することを認められた州の人口に比例して各州で配分される。 ... 下院議員の定数は人口3万人に対し1人を超えてはならないが、各州は少なくとも1人の下院議員を持たなくてはならない。 ...

下院議会の議席は有限なので、議席を完全に人口に比例して配分するには複数の州に所属する議員あるいは州に部分的に所属する議員が必要です。しかしどちらも許されていないので、議席の小数部分を公平に配分するためのアルゴリズムが憲法が施行されてから数十年間に渡っていくつも提案されました。

現在使われているアルゴリズムは Huntington-Hill (ハンティントン-ヒル) 方式、あるいは等割合方式 (method of equal proportions) などと呼ばれます。このアルゴリズムは国勢調査局の統計学者 Joseph Hill (ジョセフ・ヒル) によって 1911 年に提案され、ハーバード大学の Edward Huntington (エドワード・ハンティントン) によって 1920 年に改良されました。その後このアルゴリズムは 1941 年に連邦法 (2 U.S.C. §2a) に組み込まれ、1992 年の最高裁判所に対する異議申し立てでも撤回されることはありませんでした¹⁵。

Huntington-Hill 方式は州に一人ずつ議員を割り当てます。前処理の段階で各州に一人の議員を割り当て、メインループで 優先度 (priority) が最も高い州に議員を一人ずつ割り当てます。州の優先度は人口を \(P\) 、これまでに割り当てられた議員の数を \(r\) として \(P / \sqrt{r(r + 1)}\) と定義されます。

このアルゴリズムの疑似コードを次に示します。入力は \(n\) 個の州の人口を収めた配列 \(\mathit{Pop}[1..n]\) と割り当てようとしている議席数 \(R\) であり、\(R \geq n\) が仮定されます (現在の合衆国では \(n=50\) および \(R = 435\) です)。出力は各州に割り当てられた議席数を収めた配列 \(\mathit{Rep}[1..n]\) です。

Huntington-Hill 方式のこの実装は \(\textsc{NewPriorityQueue}\), \(\textsc{Insert}\), \(\textsc{ExtractMax}\) という操作を持つ優先度付きキューを使います (もちろん実際の法律は優先度キューに言及していません)。アルゴリズムの出力およびその正しさが、優先度付きキューがどのように実装されるかに全く依存していないことに注目してください。国勢調査局はキューとしてエクセルのスプレッドシートに収められたソート済み配列を使い、配列は反復のたびにゼロから作り直されます。ただデータ構造の学部講義を受けたあなたなら、これよりも効率的な実装を知っているでしょう。

似たような議席配分アルゴリズムは世界中の政党議会選挙で使われています。政党議会選挙では各政党に割り当てられる議席数を政党の得票数に比例させる必要があるためです。有名なのは D'Hondt (ドント) 方式¹⁶と Webster-Sainte-Laguë (ウェブスター・サン=ラグ) 方式¹⁷の二つであり、これらの方式で使われる優先度は Huntington-Hill 方式における平方根の中身をそれぞれ \(P/(r+1)\) および \(P / (2r + 1)\) としたものです。合衆国憲法が各州に最低一人の議席を割り当てることを定めていることもあって、 Huntington-Hill 方式はアメリカ合衆国下院だけでしか使われていません。

悪い例

アルゴリズムでない命令列の分かりやすい例として、次の Martin (マーティン) のアルゴリズム¹⁸を考えます:

このアルゴリズムは単純ですが、一行目が絶望的に実行困難です！ 大富豪の CEO、シリコンバレーのベンチャー投資家、ニューヨークのやり手不動産家などにとっては一行目はすぐに実行できる些細な¹⁹問題なので、この手続きはアルゴリズムかもしれません。しかしそれ以外の貧しい一般庶民に対しては処理がはっきりと示されておらず、Martin の手続きがアルゴリズムであるとは言えません。

一方で、これは帰着 (reduction) の例としては完璧です。つまり、この手続きは富豪になって税金を払わないという問題を、百万ドルを手に入れるという「より簡単な」 問題に帰着しているということです。帰着はこの本に繰り返し出てきます。何百人という実業家や政治家が示しているように、簡単な方の問題の解き方が分かれば、帰着によって難しい方の問題の解き方が分かります。

Martin のアルゴリズムおよびこれまでにあげたいくつかのアルゴリズムは、計算機科学者が考えるところのアルゴリズムではありません。なぜなら使われている処理をコンピューターで実行するのが難しいからです。この本は (基本的に) 標準的なデジタルコンピューターで普通に実装できるアルゴリズムだけを扱います。この本で説明されるアルゴリズムの各ステップは、多くのプログラミング言語で直接サポートされているもの (算術演算、代入、ループ、再帰など) か、そうでなければあなたがやり方を知っているもの (ソート、バイナリサーチ、木の走査、"\(n\) Bottles of Beer on the Wall" の歌唱など) です。

アルゴリズムの説明

アルゴリズムを正しく設計そして解析するためのスキルは、アルゴリズムを分かりやすく説明するためのスキルと結びついています。少なくとも私の講義において、アルゴリズムを完全に説明するために必要な要素は次の四つです:

• What: アルゴリズムが解く問題の明確な仕様
• How: アルゴリズムの明確な説明
• Why: アルゴリズムが解くべき問題を解くという証明
• How fast: アルゴリズムの実行時間の解析

四つの要素をこの順番で開発する必要はありません (というより、そうしない方がいいかもしれません)。問題の仕様、アルゴリズムの説明、正しいことの証明、そして実行時間の解析は同時に発展します。例えば速いアルゴリズムを得るために問題をいじったり、正しさの証明におけるトリッキーなケースに対処するためにアルゴリズムを変更したりするかもしれません。ただしそうだとしても、四つの要素を別々に示すのが読者にとって普通は最も分かりやすいでしょう。

どんな書き物もそうですが、書こうとしている説明を正しい聴衆に向けることは重要です。私が勧めているのは、疑い深く、能力があるけれども自分ほど賢くないプログラマーに向けて説明を書くことです。例えば六か月前の自分を考えてみてください。新しいアルゴリズムを開発する中で、あなたは問題とそれを解く自分のアルゴリズムに対する様々な視点からの直感を手に入れ、形式的でない証明は頭の中で行えるようになります。しかし、後になってあなたのアルゴリズムを読む人、あるいはそのアルゴリズムに基づいて書いたコードは、あなたと同じ直感や体験を共有しません。六か月後のあなたもそうです。彼らが受け取るのは、あなたが書き下した説明だけなのです。

アルゴリズムを他人に説明する必要がなかったとしても、聴衆を考えながらアルゴリズムを開発することは重要です。正確に伝えようとすれば正確に考えるからです。特に、文章を文字通りに解釈する初心者を聴衆として考えれば、自分の高レベルのアイデアがどれだけ「明らか」で「直感的」に見えたとしても、アルゴリズムを詳細に検討せざるを得ません²⁰。同様に疑い深い聴衆を考えれば、正しさと効率に関する議論は自分の直感と知性ではなくて強固な論理に基づいたものになるでしょう。

次の点はどれだけ強調してもしすぎることはありません: アルゴリズム設計者としてのあなたの一番重要な仕事は、他の人になぜ自分のアルゴリズムが動くのかを説明することです。もしアイデアを他の人間に伝えられないのなら、そんなアイデアは存在しないも同然です。正しく動いて効率の良い実行可能なプログラムを書くことは、二番目のゴールにすぎません。自分の賢さを自分自身、教官、(未来の) 雇い主、同僚、生徒に向かって見せつけることは、どんなに良くても三番目のゴールです。

問題の特定

新しいアルゴリズムの設計を始めるには、まずアルゴリズムが解く問題をきちんと定義する必要があります。同様にアルゴリズムの説明を始めるには、まずアルゴリズムが解く問題を説明する必要があります。

アルゴリズムの問題は現実世界の概念を使って通常の英語で表現されており、形式的で数学的な対象とは異なります。こういった問題を抽象的で正式な数学的対象 ――数、配列、リスト、グラフ、木など―― を使って書き直すのは、アルゴリズム設計者である我々の仕事です。私たちは問題に隠されている仮定がないかを調べ、明示しなければなりません (例えば "\(n\) Bottles of Beer on the Wall" の歌の例では \(n\) は非負の整数です²¹)。

アルゴリズムを開発する中で、仕様を改訂する必要が生じるかもしれません。例えば元の形式的でない問題の説明では指定されていなかった入出力の表現を、なんらかの表現に固定する必要が生じることがあります。また開発されたアルゴリズムが最初に目標としていた問題よりもより一般的な問題を解決することもあるかもしれません (再帰的なアルゴリズムではよくあることです)。

アルゴリズムの仕様が含むべきなのは、他の人が内部で何が起こるかを知ることなくブラックボックスとしてアルゴリズムを使うときに必要となるちょうど十分な情報です。具体的には入力の型と意味、そして出力が入力にどう依存するかです。一方、アルゴリズムの仕様はブラックボックスとしてアルゴリズムを使うときに不必要な詳細を意図的に隠すべきです。重要でないものは消しましょう。

例えば、格子掛け算アルゴリズムと農民の掛け算アルゴリズムは同じ問題を解くと言えます。なぜなら、桁の配列として表された二つの非負整数 \(x\) と \(y\) を受け取って同じように表された積 \(x \cdot y\) を計算するからです。このアルゴリズムを使う人にとって、どちらのアルゴリズムを使うかは全く重要ではありません。これに対して定規とコンパスを使ったギリシャ人のアルゴリズムが解くのは違う問題です。入出力値が桁の配列ではなく線分として与えられるからです。

アルゴリズムの説明

コンピューターで実行できるプログラムはアルゴリズムの具体的な表現です。しかしアルゴリズムはプログラムではありません。アルゴリズムとは抽象的な機械が解釈するための手続きであり、仮定している基本処理をサポートするどんなプログラミング言語でも実装できます。あなたの好きなプログラミング言語に特有な構文はアルゴリズムに全く関係ありません。構文上の細かな点を説明したとしても、本質的な部分で起こっていること²²からあなた (と読者) の気を逸らしてしまうだけでしょう。優れたアルゴリズムの説明とはコードというよりも現実のプログラムにおいてコメントとして書くべきものといった方がより近いはずです。コードは物語を伝えるのに優れた媒体ではありません。

一方で平易な英語の散文による説明も通常は良いアイデアではありません。アルゴリズムには独特な構造 ――条件文、ループ、関数呼び出し、再帰など―― があり、構造化されていない散文でアルゴリズムを表現した場合、こういった構造が分かりにくくなってしまうからです。口語英語には曖昧な語や意味が微妙に違う語がたくさん含まれるので、できるだけ明確でなくてはならないアルゴリズムの説明には向きません。散文は正確さを考えると優れた媒体ではありません。

アルゴリズムを表現する一番明確な方法は疑似コードと構造化された英語である、というのが私の意見です。疑似コードは形式的なプログラミング言語と数学の構造を使ってアルゴリズムを基本ステップに分解します。そして基本ステップは数学的な記法、純粋な英語、あるいは二つを混ぜたものなどの中から一番明確なものを使って表現されます。優れた疑似コードはアルゴリズム内部の構造を説明しつつも関係ない実装の詳細を隠すことで、アルゴリズムの理解、解析、デバッグ、実装を容易にします。

アルゴリズムの説明に含めるべき情報とは、アルゴリズムを規定し、正しさを証明し、そして実行時間を解析するために必要な全ての情報です。同時に、必要でない情報は排除しなければなりません。具体的にいうと、この本を読んでいない、能力があり疑い深いプログラマーが、なぜ動くのかを理解することなく、彼らの好きなプログラミング言語でアルゴリズムを正しくかつ素早く実装できるような説明を目指すべきです。

疑似コードを書くときの私のルールであなたをうんざりさせたくはありませんが、無意識に行ってしまいかねない特にひどい致命的な行為については注意しておかなくてはなりません。絶対に、繰り返しの処理をくだけた形で書かないでください。つまり「最初に (これを) やる。次に (あれを) やる。以下同様」あるいは「この処理を (...) まで続ける」などと書かないでください。このような文章を読んで「この処理の次に何が来るんだ？」という感想を抱いたことがある人なら分かると思いますが、アルゴリズムの最初の数ステップを説明しただけでは、後のステップで何を行うかはほとんどあるいは全く分かりません。もしアルゴリズムにループが含まれるのなら、ループとして書いてください。そしてループの各反復で何が起こるのかを明示的に書いてください。同様に、もしアルゴリズムが再帰的ならば、再帰的に書き、場合分けとそれぞれの場合で何をするのかを明示的に書いてください。

アルゴリズムの解析

アルゴリズムをただ書き下して「見よ！」というだけでは不十分で、アルゴリズムがすべきことを効率良く行うことを聴衆 (および自分自身) に納得させなければなりません。

正しさ

アプリケーションが置かれる環境によっては、プログラムが「常識的な」入力の全てに対してほとんどの場合に正しく動けばそれで OK とされることもあります。しかし、この本では違います。アルゴリズムは全ての可能な入力に対して常に正しいことを要求されます。加えて、アルゴリズムが正しいことは証明されなければなりません。直感に頼ったり、テストケースをいくつか通すだけでは不十分です。

講義の前半で見るアルゴリズムについては正しさが本当に明らかなことがありますが、「明らかである」が「間違っている」の同義語であることが本当によくあります。この講義で扱うアルゴリズムのほとんどは正しさの証明に苦労が伴います。なお正しさの証明には帰納法をよく使います。私たちは帰納法が大好きです。帰納法は友達です²³。

もちろん、きちんとした証明を行うには、その前にアルゴリズムが何をするのかをきちんと説明しておく必要があります！

実行時間

同じ問題に対する異なるアルゴリズムをランク付けする最も一般的な方法は、どれだけ速く実行できるかで並べるというものです。理想的には、どんな問題に対しても可能なもののうち一番早いアルゴリズムが望まれます。アプリケーションが置かれる環境によっては全ての「常識的な」入力に対してほとんどの場合に速く動けばそれで OK ということもありますが、この本では違います。アルゴリズムはワーストケースにおいても常に効率良く実行できることが求められます。

実行時間をどうやって測るべきでしょうか？ 例えば \(\textsc{BottlesOfBeer}(n)\) を歌うにはどれだけの時間がかかるでしょうか？ 実行時間が入力 \(n\) の関数であることは明らかですが、実行時間は歌を歌う速さにも依存しています。バースを歌うのに 10 秒かける歌手もいますし、20 秒かける歌手もいるでしょう。技術を使うとさらに極端なことができます: モールス信号を使ってテレグラフで歌を書き留めたらバースにまる一分かかるでしょう。あるいはウェブから mp3 をダウンロードするならバースあたり十分の一秒で済みますし、 mp3 をコンピューターのメインメモリ上で複製するのはバースあたり数マイクロ秒しかかかりません。

このような場合に重要となるのは、\(n\) が大きくなるにつれて歌うのにかかる時間が時間がどう変化するかです。\(\textsc{BottlesOfBeer}(2n)\) を歌うには \(\textsc{BottlesOfBeer}(n)\) を歌うときの 2 倍の時間がかかり、この事実は技術と関係がありません。歌唱時間の漸近表記 \(\Theta(n)\) はこれを意味しています。

アルゴリズムの実行時間を調べるときには、アルゴリズムがある命令を何回実行するか、あるいはコード中のある場所に処理が何回到達するかを測定します。例えば "beer" という単語は \(\textsc{BottlesOfBeer}\) のバースにつき 3 回出てくるので、"beer" と何回歌ったかは歌唱時間の良い指標となります。この問題に対しては正確な答えが求まります: \(\textsc{BottlesOfBeer}(n)\) を歌うと "beer" はちょうど \(3n + 3\) 回歌われます。

ちょうどよいので触れておくと、多項式時間の歌唱時間を持つ歌はたくさんあります。次に示すのはほとんどの英語話者になじみのある歌です:

\(\textsc{NDaysOfChristmas}\) の入力は \(n-1\) 個のプレゼントが入ったリストであり、ここでは配列として表されます。歌唱時間が \(\Theta(n^2)\) であることを示すのは簡単です。正確に言うとプレゼントの名前はちょうど \(\sum_{i=1}^{n} i = n(n+1)/2\) 回歌われます (partridge in a pear tree を含む)。またクリスマスの最初の \(n\) 日で my true love がちょうど \(\sum_{i=1}^{n} \sum_{j=1}^{n} j\ =\) \(n(n+1)(n+2)/6\ =\) \(\Theta(n^3)\) 個のプレゼントをくれるというのも簡単に示せます。

多項式歌唱時間の歌は他には "Old MacDonald Had a Farm", "There Was an Old Lady Who Swallowed a Fly", "Hole in the Bottom of the Sea", "Green Grow the Rushes O", "The Rattlin' Bog", "The Court Of King Caractacus", "The Barley-Mow", "If I Were Not Upon the Stage", "Star Trekkin'", "Ist das nicht ein Schnitzelbank?"²⁴, "Il Pulcino Pio", "Minkurinn í hænsnakofanum", "Echad Mi Yodea", そして "\(T o\) \(\kappa o \kappa o \rho \acute{\alpha} \kappa \iota\)" があります。これ以上はお好きな保育園に聞いてください。

もっと奇妙な歌唱時間を持つ歌もあります。現代的な例は Guy Steele (ガイ・スティール) による "The TELNET Song" であり、この歌は最初の \(n\) 個のバースを歌うのに \(\Theta(2^{n})\) の時間がかかります (Steele は \(n=4\) を勧めています)。それからもちろん、終わらない歌もあります²⁵。

"The TELNET song" を除くと、これまでに紹介した歌はどれも入れ子になった小さなプールで表現される反復アルゴリズムであり、実行 歌唱時間は入れ子になった和で求めることができます。これに対して、再帰的なアルゴリズムの実行時間は再帰方程式を使って表現した方が自然です。例えば農民の掛け算アルゴリズムは次のように表されました: \[ x \times y = \begin{cases} 0 & \text{if } x = 0 \\ \lfloor x / 2 \rfloor \times (y + y) & \text{if } x \text{ が偶数} \\ \lfloor x / 2 \rfloor \times (y + y) + y & \text{if } x \text{ が奇数} \\ \end{cases} \]

このアルゴリズムを使って \(x \cdot y\) を計算するのに必要なパリティ検査、足し算、mediation 演算の数を \(T(x, y)\) とすると、この関数は再帰的な不等式 \(T(x, y) \leq T(\lfloor x/2 \rfloor, 2y) + 2\) および基底ケース \(T(0, y) = 0\) を満たします。次の章で説明されるテクニックを使うと上界を求めることができ、\(T(x,y) = O(\log x)\) と分かります。

アルゴリズムの実行時間が、サブルーチンで利用されるデータ構造の実装に依存することもあります。例えば Huntington-Hill の配分アルゴリズム \(\textsc{ApportionCongress}\) の実行時間は \(O(N + RI + (R - n)E)\) と表すことができ、ここで \(N\) は \(\textsc{NewPriorityQueue}\) の実行時間、\(I\) は \(\textsc{Insert}\) の実行時間、\(E\) は \(\textsc{ExtractMax}\) の実行時間です。\(R \geq 2n\) という常識的な仮定 (どの州にも平均して二つの議席が割り当てられるという仮定) を置くと上界を \(O(N + R(I + E))\) と単純化でき、この実行時間は使用される優先度付きキューの実装に依存します。国勢調査局では優先度付きキューをソートされていない配列を使って実装するので \(N = 1 = \Theta(1)\) および \(E=\Theta(n)\) であり、\(\textsc{ApportionCongress}\) の実行時間は \(O(Rn)\) です。しかし二分ヒープまたはヒープで順序付けされた配列を使って優先度付きキューを実装すると \(N = \Theta(1)\) および \(I = E = O(\log n)\) となるので、アルゴリズム全体の実行時間は \(O(R \log n)\) となります。

最後に、アルゴリズムを解析する上で実行時間以外のリソース、例えば空間、コイン投げの回数、キャッシュのページフォルトの回数、プロセス間通信の数、my true love が私にくれるプレゼントの数、などが重要になることがあります。こういったリソースも実行時間を解析するのと同じテクニックを使って解析できます。例えば \(n\) 桁の整数の格子掛け算が消費する空間は、部分積を全て書き留めておくなら \(O(n^{2})\) であり、必要となるたびに計算するのであれば \(O(n)\) です。

練習問題

1. 名前を直訳すると 「Adbdulla の父、Moses の子、Khwārizmī 人の Mohammad」となります。Khwārizmī はウズベキスタンの Khorezm (ホラズム) 州にあった古代都市で、現在では Kiva (ヒヴァ) と呼ばれます。^[return]

2. タイトルを直訳すると「約分と消約による計算についての概説」となります。^[return]

3. Liber Abaci は「アバカスについての書」と翻訳したくなるかもしれませんが、より正確な訳は「計算についての書」です。Fibonacci の時代の前も後も、イタリア語 abaco は計算のための機械、技法、学校、書物など、数値計算に関するもの全てを指します。これは英語における "computer science" という語の使われ方と似ています。また、オペレーションリサーチに対応する中国語 ("運籌學") を直訳すると「物を数えるときに使う棒についての学問」となることにも似ていると言えるでしょう。^[return]

4. calculate (計算) という語は「小さい石」を意味するラテン語の calculus が語源です。この石は計算のとき表の上に置く石、つまり詩人チョーサーが言うところの augrym stone のことです。紀元前 440 年、Herodotus (ヘロドトス) は著書『歴史』にこう書いています:「計算をしてその結果を書き留める ("\(\lambda o \gamma \acute{\iota} \zeta \varepsilon \sigma \theta \alpha \iota\, \) \(\psi \acute{\eta} \phi o \iota \varsigma\)" 直訳すると「計算して小石を敷き詰める」) ときギリシャ人は左から右に向かって書くが、エジプト人はその逆である。しかしエジプト人に聞くと、彼らは数を右に向かって書いていると言い、ギリシャ人は左に向かって書いていると言う」 (奇妙なことに、 Herodotus はエジプト人が卵をどちら側から食べるかについては疑問に思わなかったようです)^[return]

5. ☞ Reckoning with digits! ☜^[return]

6. ギリシャ語の接頭語 "algo-" が「技法」あるいは「解説」を意味すると記している中世の資料がいくつかあります。また他の資料を見ると、algorithm という語を発明したのがギリシャの哲学者だったり、インドの王だったり、"Algus" や "Algor"、または "Argus" という名のスペイン王だったりします。 Dante Alighieri (ダンテ・アリギエーリ) の著作をおそらくは含むいくつかの文献では、語源となった神話上のギリシャ人造船技師 (Argonaut) が特定されています。これらの全く誤っている主張が歴史的な正確さを求めてなされたのか、それともただの記憶を助けるための作り話だったのかははっきりしません。^[return]

7. タイトルを直訳すると『安産のための薬』！ Pappus of Alexandria (アレキサンドリアのパップス) という人物が Eutocius よりも約 200 年前に同じ本 \(\Omega \kappa \upsilon \tau \acute{o} \kappa \iota o \nu\) の抜粋をいくつか複写したという記録が残っています。しかしその抜粋が格子アルゴリズムの説明を含んでいるかは分かっておらず、この抜粋も失われていています。^[return]

8. シュメール人が巨大な数の計算を 60 進の位取り記数法で正確に行っていたことについては十分な証拠があります。しかし彼らが実際に使った計算方法についての現存する記録を私は見たことがありません。また通常の乗算表と逆数表に加えて 1 から 59 までの整数の二乗を刻んだ表が見つかっており、このことをもってバビロニア人が \(xy = ((x + y)^2 - x^2 - y^2) / 2\) のような等式を使って乗算を計算していたとする数学史家もいます。しかしこのテクニックが使えるのは \(x < 60\) のときだけであり、バビロニア人が \(x > 60\) についてどのように \(x^2\) を計算していたのかは分かりません。^[return]

9. これによって歴史的な対立を焚き付けてしまうかもしれません: ギリシャ人とエジプト人、リリパット人とブレフスキュ人、Mac と PC、ゼロが自然数に含まれると考える人と間違っている人。^[return]

10. ソース: Biblioteca nazionale Braidense (Milano) (パブリックドメイン)。^[return]

11. ソース: https://archive.org/details/archimedisopera05eutogoog/page/n377 (パブリックドメイン)。^[return]

12. リンド数学パピルスに記されているアルゴリズムは mediation とパリティを使いませんが、比較は使います。このアルゴリズムは事前に二つの表を作成しておくことで、数を 2 で割らなくても済むようにしています。表の一つは \(x\) より小さい 2 のべきを並べたもので、もう一つの表はその 2 のべきに \(y\) を掛けたものです。貪欲な引き算によって \(x\) を分解したときに現れる 2 のべきが一つ目の表から選ばれ、それに対応する二つ目の表の要素を足し上げることで積が計算されます。^[return]

13. 1 から 9 までの数字は Fibonacci の Liber Abaci より少なくとも二世紀前から「ゴバール数字 (gobar numerals)」という名前でヨーロッパに知られていました。この名前はちりを意味するアラビア語 ghubār から取られており、意味をたどっていくと砂で覆われたテーブルを使って計算を行うインド人の習慣にたどり着きます。またギリシャ語の \(\ddot{\alpha} \beta \alpha \xi\) の語源はラテン語の abacus であり、これも元々は砂で覆われたテーブルを指します。^[return]

14. 幾何学を表す英単語 "geometry" が何を意味するか覚えていますか？ Democritus (デモクリトス) は後にエジプト人測量技師のことをいくらか嘲笑的に arpedonaptai (\(\acute{\alpha} \rho \pi \varepsilon \delta o \nu \acute{\alpha} \pi \tau \alpha \iota\)) と呼びました。これは "ロープを絞める人" を意味します。^[return]

15. 最高裁判所はそれまでの連邦地方裁判所の判決を覆し、信義則に則って採択された (adopted by good faith) どんな議席の配分方法も憲法に違反しないと全会一致で表明しました。現在使われている議席配分のアルゴリズムは合衆国国勢調査局のウェブサイト http://www.census.gov/topics/public-sector/congressional-apportionment.html で詳細に説明されています。また議席配分の問題に関する歴史は http://www.thirty-thousand.org/pages/Apportionment.html に詳しく載っています。様々な議席配分法を解説した議会調査局によるレポートは http://www.fas.org/sgp/crs/misc/R41382.pdf から手に入ります。^[return]

16. Thomas Jefferson (トーマス・ジェファーソン) によって 1792 年に考案され、1792 年から 1832 年まで合衆国の議席配分に使われました。1878 年にベルギー人数学者 Victor D'Hondt (ビクター・ドント) によって再発見され、1888 年にスイス人物理学者 Eduard Hagenbach-Bischoff (エドアルド・ハーゲンバハ・ビスチョフ) によって改良されました。^[return]

17. Daniel Webster (ダニエル・ウェブスター) によって 1832 年に考案され、1843 年から 1911 年まで画集国の議席配分に使われました。1910 年にはフランス人数学者 André Sainte-Laguë (アンドレ・サン=ラグ) によって、1980 年にはドイツ人物理学者 Hans Schepers (ハンス・シェーパース) によって再発見されました。^[return]

18. Steve Martin, You Can Be A Millionaire, Saturday Night Live, January 21, 1978. および Comedy Is Not Pretty, Warner Bros. Records, 1979.^[return]

19. "ブロックチェーンとディープラーニングを使った量子でセキュアな"^[return]

20. とりわけ、私はあなたが疑い深い初心者であると仮定します！^[return]

21. "\(\sqrt{2}\) Bottles of Beer on the Wall" と歌っている人を見たことはありませんが、"\(\aleph_{0}\) Bottles of Beer on the Wall" と歌っている集合理論学者なら何回か見たことがあります。どういうわけか彼らはいつも歌い終わる前に歌うのを止めていました。^[return]

22. もちろんこれは宗教的信念に関わる話題です。安楽椅子言語学者が絶え間なく議論を交わしている Sapir-Whorf (サピア-ウォーフ) 仮説においては、人は使う言語に紐づいた区分でしか考えることができないとされます。この仮説に関する極端な意見によると、ある言語における概念の中には他の言語話者に理解できないものがあり、それは技術が発展していない ――"jump the shark" や "Fortnite streamer" をアラム語に訳せるとは思いません―― ためではなく、言語と文化における固有の構造上の差異があるためであると言います。これよりも疑い深い視点については Steven Pinker (スティーブン・ピンカー) の『言語を生み出す本能 (The Language Instinct)』を見てください。異なるプログラミングパラダイムについてもこのアイデアはいくらか当てはまるでしょう: 「Y コンビネータがまた出てきた、なんだっけ？」「テンプレートってどうなってるの？」「Abstract Factory って何？」などです。幸いこの本が触れる分野ではプログラミング言語間の差異は十分小さく、大きな影響はありません。説得力のある反例としては、Chris Okasaki (クリス・オカサキ) による専門書 Functional Data Structures および最近のその続編を見てください。^[return]

23. 帰納法があなたの友達ではない場合、本を読むのに骨が折れるでしょう。^[return]

24. Ja, das ist Otto von Schnitzelpusskrankengescheitmeyer!^[return]

25. They just go on and on, my friend.^[return]

26. Ja, das ist das Subatomarteilchenbeschleunigungsnaturmäßigkeitsuntersuchungsmaschine!^[return]

27. グラスの名前は次の中から選ばれます: nipperkin, quarter-gill, half-a-gill, gill, quarter-pint, half-a-pint, pint, quart, pottle, gallon, half-anker, anker, firkin, half-barrel/kilderkin, barrel, hogshead, pipe/butt, tun, well, river, ocean。最後のいくつかの例外を除いて、各グラスの容量は一つ前のグラスの倍です。アイルランドとスコットランドで歌われているバージョンでは歌詞が少し違っており、"gallon" の後は人が続きます (barmaid, landlord, drayer など)。
    
    John Marston (ジョン・マーストン) によって 1600 年ごろに書かれた戯曲 Jack Drum's Entertainment (あるいは the Comedie of Pasquill and Katherine) には "Give us once a drink" という曲の古いバージョンが出てきます。("Giue vs once a drinke for and the black bole. Sing gentle Butler bally moy!") しかし、Marston が "high Dutch Song" を戯曲のために書いたのどうか、"bally moy" は "barley mow" の聞き間違い (mondegreen) なのかそれとも逆か、そもそも二つの曲が同じなのかどうか、学者の意見は一致しません。 これについて議論するなら \(n\) 本のビールと一緒にやるのが一番でしょう。^[return]