閉路の検出
閉路を含まない有向グラフを有向非巡回グラフ (directed acyclic graph, DAG)と呼びます。ある頂点に向かう辺が無い場合、その頂点をソース (source) と言い、ある頂点から出る辺が無い場合、その頂点をシンク (sink) と言います。辺が一つも付いていない孤立した頂点はソースかつシンクです。任意の DAG には少なくとも一つのソースとシンクがありますが、複数あることもあります: 例えば辺が無いグラフでは全ての頂点がソースかつシンクです。
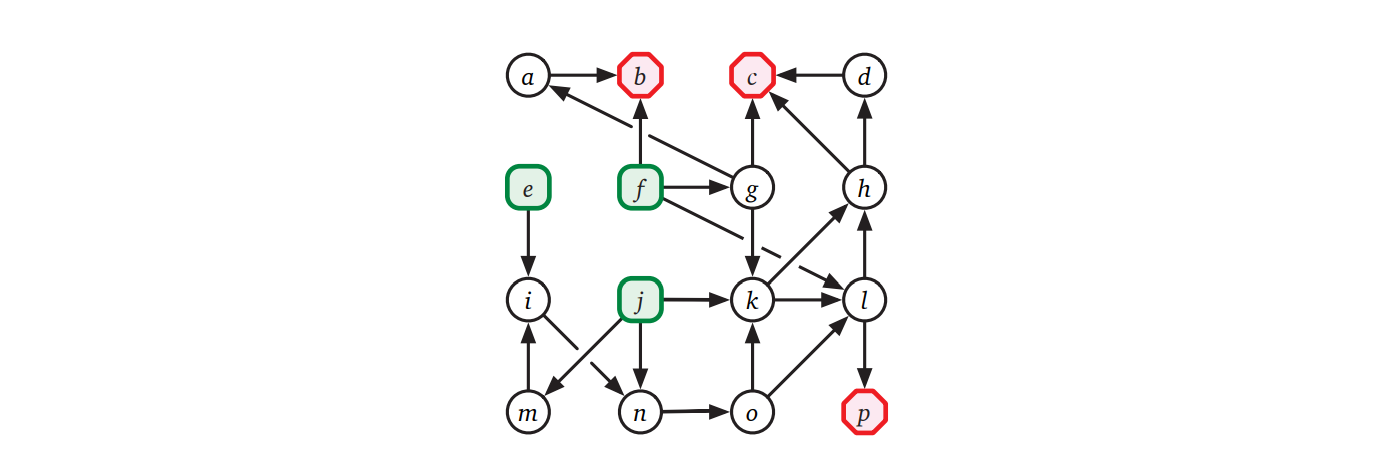
前節で示した、\(\mathit{u.post} < \mathit{v.post}\) を満たす任意の辺 \(u \rightarrow v\) には \(v\) から \(u\) への有向路があるという事実を思い出してください。この事実を使えば、頂点を帰りがけ順に並べてから全ての辺を総当たりで調べることで与えられた有向グラフが DAG かどうかを \(O(V+E)\) 時間で判定できます。
頂点に番号を振っていく代わりに頂点の状態を直接管理して、アクティブな頂点への辺が検出された時点で \(\textsc{False}\) を返すようにしても同様に閉路を検出できます。このアルゴリズムの実行時間も \(O(V+E)\) です。
procedure \(\texttt{IsAcyclic}\)(\(G\))
for 頂点 \(v\) do
\(\mathit{v.status} \leftarrow \textsc{New}\)
for 頂点 \(v\) do
if \(\mathit{v.status} = \textsc{New}\) then
if \(\texttt{IsAcyclicDFS}\)(\(v\)) \(= \textsc{False}\) then
return \(\textsc{False}\)
return \(\textsc{True}\)
procedure \(\texttt{IsAcyclicDFS}\)(\(v\))
\(\mathit{v.status} \leftarrow \textsc{Active}\)
for \(v \rightarrow w\) の形をした辺 do
if \(\mathit{w.status} = \textsc{Active}\) then
return \(\textsc{False}\)
else if \(\mathit{w.status} = \textsc{New}\) then
if \(\texttt{IsAcyclicDFS}\)(\(w\)) \(= \textsc{False}\) then
return \(\textsc{False}\)
\(\mathit{v.status} \leftarrow \textsc{Finished}\)
return \(\textsc{True}\)