高速乗算

前章では、\(n\) 桁の数の乗算を \(O(n^{2})\) で行う古くからあるアルゴリズムをいくつか紹介しました。小学校で習う格子アルゴリズムや、エジプト人農民の乗算アルゴリズムです。

桁ごとの数を収めた配列を分割して、さらに次の等式を使えばもっと効率の良いアルゴリズムが作れそうです: \[ (10^{m}a + b)(10^{m}c + d) = 10^{2m}ac + 10^{m}(bc + ad) + bd \] この再帰方程式から以下に示す分割統治法を使ったアルゴリズムが作れます。\(n\) 桁の整数 \(x\) と \(y\) の積を計算するアルゴリズムであり、\(ac, bd, ad, bd\) という部分積を再帰的に計算しています。最後の行の乗算は再帰的になっていませんが、\(10\) を掛ける処理は桁をひとつずらすことに対応するので、\(O(n)\) 時間で行えます。

このアルゴリズムの正しさは帰納法で簡単に証明できます。実行時間は次の再帰方程式を満たします: \[ T(n) = 4T(\lceil n/2 \rceil) + O(n) \]

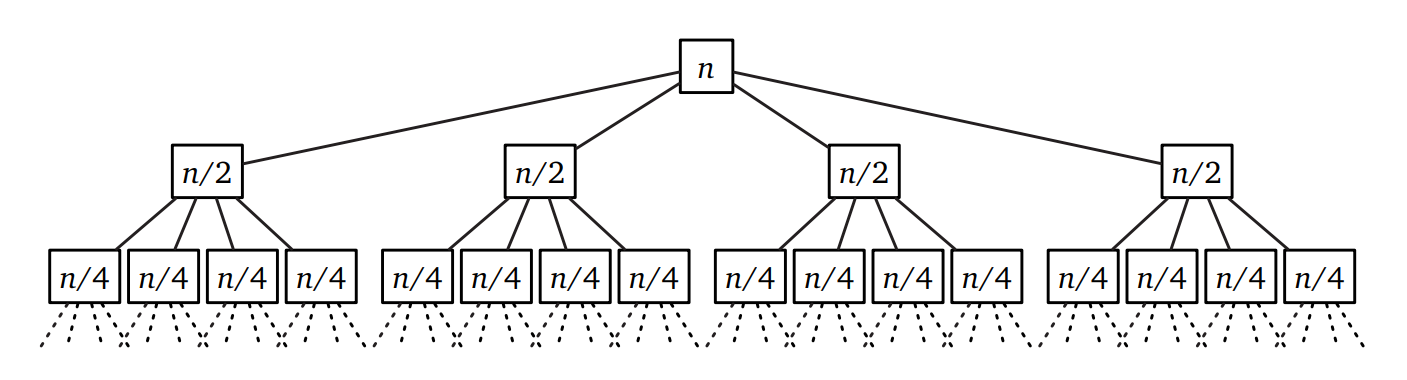
再帰木の方法を使うと、再帰方程式は増加幾何級数となることが分かります。つまり \(T(n) =\) \(O(n^{\log_{2} 4}) =\) \(O(n^{2})\) です。結局、このアルゴリズムは格子アルゴリズムと同じように \(x\) と \(y\) の各桁をかけているだけなのです。だからこのアルゴリズムでは高速化できません。残念、うまくいくと思ったんですが。

二十世紀を代表する数学の巨人の一人である Andrei Kolmogorov (アンドレイ・コルモゴロフ) は 1950 年代の中頃、 \(n\) 桁の乗算を \(o(n^{2})\) で行うアルゴリズムは存在しないという予想を発表しました。1960 年、Kolmogorov はモスクワ大学で開かれたセミナーで自身の "\(n^{2}\) 予想" を再表明し、これに関連する問題をこれからの議題として提案しました。それからちょうど一週間後、Anatolii Karatsuba (アナトリー・カラツバ) という 23 才の学生が Kolmogorov のもとを訪れ、注目すべき反例を示しました。Karatsuba 本人によると:

セミナーが終わってから、\(n^{2}\) 予想を否定的に解決する新しいアルゴリズムについて Kolmogorov に伝えた。成り立つはずだと思っていた予想と矛盾するアルゴリズムを見て、Kolmogorov はとても当惑したようだった。次のセミナーの場で Kolmogorov は私のアルゴリズムを自分で参加者に説明し、セミナーはそこで終了となった。

Karatsuba が気付いたのは、中央の \(bc + ad\) という係数が他の係数 \(ac\) と \(bd\) から計算でき、そのときに再帰的な掛け算が一度しか必要にならないということでした。つまり、次の代数的等式です: \[ ac + bd - (a - b)(c - d) = bc + ad \] このトリックを使って上述のアルゴリズムを書き換えると、再帰的な呼び出しが三回で済みます:

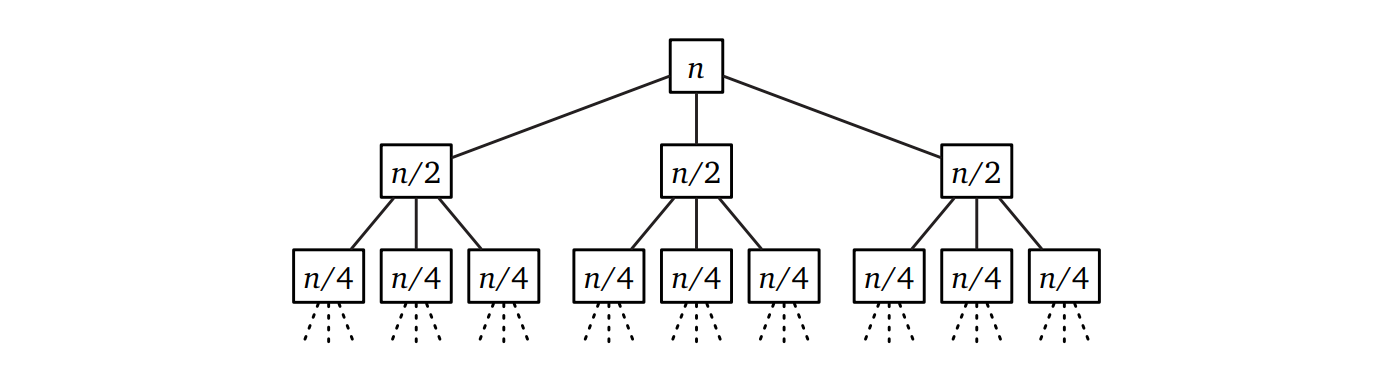
Karatsuba のアルゴリズム \(\textsc{FastMultiply}\) の実行時間が従う再帰方程式は以下です: \[ T(n) \leq 3 T(\lceil n/2 \rceil) + O(n) \] ここでも、再帰的な議論においては天井関数を無視しても構いません。再帰木の方法を使うと再帰方程式は増加幾何級数となりますが、この場合の解は \(T(n) = \) \(O(n^{\lg 3}) = \) \(\pmb{O(n^{1.58496})}\) であり、二次関数だった以前のアルゴリズムから驚くべき高速化です¹。Karatsuba のアルゴリズムがアルゴリズムの設計と解析という行為を正式な研究の対象にしたと言っても過言ではありません。

Karatsuba のアイデアを推し進めて数をさらに複雑に切り分けると、さらに高速な乗算アルゴリズムを得ることができます。Andrei Toom (アンドレイ・トゥーム) は、任意の整数を \(k\) 個の部分に分け、これら \(n/k\) 桁の部分の間の再帰的な乗算を \(2k - 1\) 回だけ使って元の積を計算するというアルゴリズムの無限クラスを発見しました。Stephen Cook (スティーブン・クック) は自身の博士論文において Toom のアルゴリズムの単純にしたものを示しています。任意の固定された \(k\) について、Toom-Cook のアルゴリズムの実行時間は \(O(n^{1 + 1/(\lg k)})\) です。ここで \(O(\cdot)\) に隠れている定数部分は \(k\) に依存します。

Carl Friedrich Gauss (カール・フリードリヒ・ガウス) による高速フーリエ変換 (fast fourier transform)² の発見も、元をたどればこの分割統治による戦略を使っていると言えます。基本的なFFT アルゴリズムの実行時間は \(O(n \log n)\) であり、 FFT を整数の乗算に使うと多少のオーバーヘッドが生じます。FFT を使った最初の整数乗算アルゴリズムは Arnold Schönhage (アーノルド・ショーンハーゲ) と Volker Strassen (フォルカー・ストラッセン) によって 1971 年に発表されており、その実行時間は \(O(n \log n \log \log n)\) です。Schönhage-Strassen のアルゴリズムはその後数十年に渡って最速の整数乗算アルゴリズムであり続けました。後に技術的な改善が Martin Fürer によって発見され、ついに 2019 年には David Harvey と Joris van der Hoeven が \(O(n \log n)\) 時間で整数の積を計算するアルゴリズムを発表しました³。

1. 私の説明は実際に起こったことと少しだけ異なっています。Karatsuba が提案したのは \((a + b)(c + d) - ac - bd = bc + ad\) という等式に基づいたアルゴリズムでした。この場合でも実行時間は \(O(n^{\lg 3})\) ですが、再帰方程式が汚くなります。\(a - b\) と \(c - d\) は \(m\) 桁ですが、 \(a + b\) と \(c + d\) が \(m + 1\) 桁となるためです。本文で示した単純化は Donald Knuth (ドナルド・クヌース) によるものです。^[return]

2. 高速フーリエ変換については私の講義ノートがあります: http://algorithms.wtf/^[return]

3. Schönhage-Strassen のアルゴリズムは 75,000 桁以上の整数に対する実用上最速の乗算アルゴリズムです。Fürer, Harvey, Hoeven らが提案したアルゴリズムが "実用上" 高速となるのは、桁数が宇宙に存在する粒子より大きい整数でだけです。^[return]