練習問題

Hanoi の塔

以下に示す再帰的でないアルゴリズムがそれぞれ上述した再帰的なアルゴリズムと全く同じ操作を行うことを示してください。同じ円盤を、同じ杭から同じ杭に、同じ順番で動かすことを示してください。三つの杭を $0$, $1$, $2$ で表し、$n$ 個の円盤を $0$ から $2$ に移動させるとします (図 1.1 参照)。
1. $n$ が偶数ならば、杭 $1$ と $2$ の名前を交換する。$i$ 番目のステップにおいて、杭 $i \text{ mod } 3$ を使わないで行える唯一の操作を行う。もし行える操作がないならば、全ての円盤が杭 $i \text{ mod } 3$ にあるので、パズルは解けている。
2. 最初の操作として、$n$ が偶数なら円盤 $1$ を杭 $1$ に、$n$ が奇数なら円盤 $1$ を杭 $2$ に移動させる。それ以降は可能な操作のうち直前の操作で使わなかった円盤を使う (唯一の) ものを行う。もし可能な操作が存在しない場合、パズルは解けている。
3. 円盤 $n+1, n+2, n+3$ がそれぞれ杭 $0, 1, 2$ にあるとして、次の条件を満たす操作を可能な限り繰り返す。
  - 奇数の円盤を他の奇数の円盤のすぐ上に置かない。
  - 偶数の円盤を他の偶数の円盤のすぐ上に置かない。
  - 直前の動作を打ち消さない。
4. $\rho(n)$ で $n / 2^{k}$ が整数でないような最小の $k$ を表すことにする。例えば $42 / 2^{1}$ は整数だが $42 / 2^{2}$ は整数でないので $\rho(42) = 2$ である (同値な定義として、$\rho(n)$ を $n$ を二進法表したときの最下位の $1$ の位置に $1$ を足したもの、とすることもできる)。$\rho(n)$ は振る舞いが定規の目盛りに似ているので、定規関数 (ruler function) と呼ばれることがある。この関数を使った以下のアルゴリズム:
  
  procedure $\texttt{RulerHanoi}$($n$)
  
  $ i \leftarrow 1 $
  
  while $ \rho (i) \leq n $ do
  
  if $n - i$ が奇数 then
  
  円盤 $\rho(i)$ を前に動かす $\quad$ ⟨⟨$0 \rightarrow 1 \rightarrow 2 \rightarrow 0$⟩⟩
  
  else
  
  円盤 $\rho(i)$ を後に動かす $\quad$ ⟨⟨$0 \rightarrow 2 \rightarrow 1 \rightarrow 0$⟩⟩
  
  return $i \leftarrow i + 1$
チャイニーズリング、九連環、Chinese linked rings、Baguenaudier、Cardan's Rings (カルダノの輪)、Meleda、Patience、Tiring Irons、Prisoner's Lock、Spin-Out など様々な名前で呼ばれる中国由来のパズルがあり、このパズルは Hanoi の塔パズルの古い先祖とみなすことができます。このパズルは十六世紀には中国とヨーロッパの両方でよく知られており、イタリア人数学者 Luca Pacioli (ルカ・パチョーリ) は未発表の著作 De Viribus Quantitatis でこのパズルの輪が七つのバージョンを解法と共に説明しています¹。この著作が書かれたのは 1498 年から 1506 年の間のことでしたが、それから数年後、明の詩人の楊慎は輪が九つのバージョンを「女子供のためのおもちゃ」と表現しています。出典は不確かですが、一説によるとこのパズルは二世紀に中国の将軍が、自分が戦争に出ている間に妻が時間をつぶせるようにと作らせたのが起源だそうです。

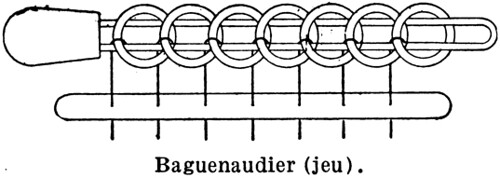図 1.16

カルダノの輪²

チャイニーズリングにはいろいろな種類がありますが、もっともよく知られているのは長い金属のループといくつかの小さい輪、小さい輪につながった両端が輪になった棒、その棒の反対側につながったベースからなります。ループには上図のように小さな輪が突き刺さっていて、この小さな輪を全て取り除くのがパズルのゴールとなります。

このパズルを次のように抽象化します。各リングの状態を $0$ か $1$ で表し、 $1$ がリングがループに通っていることを、 $0$ がリングがループから離れていることを表します (リングの添え字は出口に近い方が若い番号となります)。このパズルで許されている操作は次の通りです:
- 一番目の (一番出口に近い) ビットはいつでも反転できる。
- パズルの状態を表すビット列がちょうど $z$ 個の $0$ で終わるならば、$z + 2$ 番目のビットを反転できる。
パズルのゴールは $1$ だけの状態から $0$ だけの状態に遷移させることです。例えば、次の 21 回の操作は輪が 5 個のパズルを解きます。 \[ \begin{aligned} \texttt{11111} & \xrightarrow{1} \texttt{11110} \xrightarrow{3} \texttt{11010} \xrightarrow{1} \texttt{11011} \xrightarrow{2} \texttt{11001} \xrightarrow{1} \texttt{11000} \\ & \xrightarrow{5} \texttt{01000} \xrightarrow{1} \texttt{01001} \xrightarrow{2} \texttt{01011} \xrightarrow{1} \texttt{01010} \xrightarrow{3} \texttt{01110} \\ & \xrightarrow{1} \texttt{01111} \xrightarrow{2} \texttt{01101} \xrightarrow{1} \texttt{01100} \xrightarrow{4} \texttt{00100} \xrightarrow{1} \texttt{00101} \\ & \xrightarrow{2} \texttt{00111} \xrightarrow{1} \texttt{00110} \xrightarrow{3} \texttt{00010} \xrightarrow{1} \texttt{00011} \xrightarrow{2} \texttt{00001} \xrightarrow{1} \texttt{00000} \end{aligned} \]
1. ♦ ある操作が直前の動作と同じでないとき、その動作を既約と呼ぶことにします。任意の非負整数 $n$ について、輪が $n$ 個あるチャイニーズリングパズルを解く既約な操作の列はちょうど一つだけ存在することを示してください。[ヒント: グラフを知っている場合、この問題はとても簡単になります。]
2. チャイニーズリングパズルを解くアルゴリズムを説明してください。アルゴリズムの入力は輪の数 $n$ であり、出力はパズルを解く既約な操作の列です。例えば整数 $5$ が入力された場合のアルゴリズムの出力は $1, 3, 1, 2, {}$$1, 5, 1, 2, {}$$1, 3, 1, 2, {}$$1, 4, 1, 2, {}$$1, 3, 1, 2, 1$ です。
3. 前問のアルゴリズムが出力する操作列の長さを $n$ の関数として表してください。その答えが正しいことを証明してください。
Hanoi の塔に関するあまり知られていない話をしましょう。十三世紀、寺院を Benares から Pisa に移築したときのことです。この移築は裕福な商人であり数学者でもあった Leonardo Fibonacci が、神聖ローマ皇帝フリードリヒ 2 世の命を受けて行いました。教皇は十字軍から帰還した兵士たちから寺院について聞いていたのです。この移築によって Pisa の塔とそこに住む僧侶たちは有名になり、イタリア半島において Pisa が交易の中心となるきっかけの一つとなりました。

しかしこの移築が完了して早々、不幸な事件が起こりました。ダイアモンドの棒が傾いてしまったのです。これを受けて Fibonacci は、棒が傾きすぎて使えなくなってしまわないよう円盤を動かすルールを緩めました: 傾いている棒に刺さっている円盤は、他の棒へ一度に移動させても構わないことにしたのです。引き続き大きな円盤を小さな円盤の上に置くのは禁止され、垂直な棒から円盤を動かすときには円盤は一つずつしか移動させることはできません。

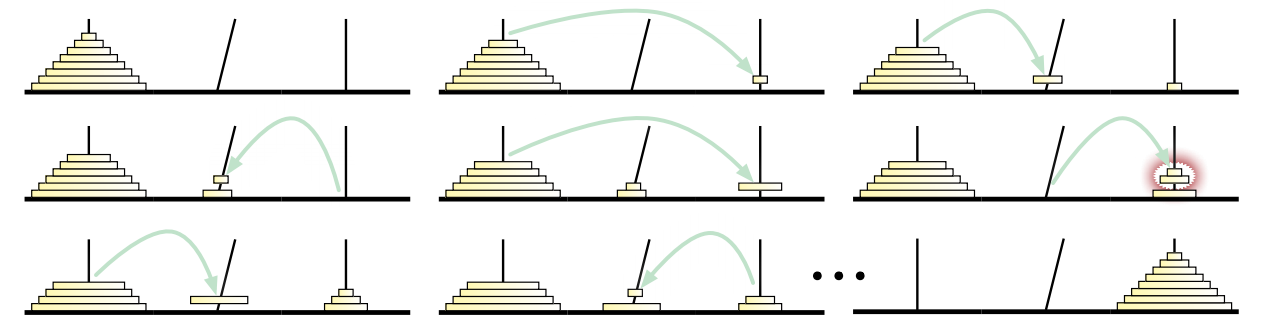図 1.17

Pisa の塔 (五番目の操作で二つの円盤が傾いた棒からまとめて移動されている)

Fibonacci が定めた新しいルールによって、Pisa に移り住んだ司祭たちは Benares にいたときよりもいくらか速く宇宙の終わりを迎えられるようになりました。しかし幸いにも新しく教皇となったグレゴリウス 9 世がフリードリヒ 2 世を破門し、寺院は Pisa から Benares に返還されたので、異国の奇妙な数学的儀式に興味を持つ司祭は減っていきました。それからしばらくして、寺院がかつてあった場所に鐘楼が建てられましたが、この建物は建設されるやいなや傾いてしまったといいます³。

垂直な棒からもう一つの垂直な棒へ $n$ 個の円盤を最小回数の操作で移動させるアルゴリズムを説明、解析してください。アルゴリズムが実行する操作は正確に何回ですか？
次に示す制限されたHanoi の塔パズルに関する問に答えてください。三つの杭を $0, 1, 2$ で表し、$n$ 個の円盤を $0$ から $2$ に移動させることがゴールです。
1. 杭 $1$ から杭 $2$ に円盤を移動させるのが禁止されているとします。つまり、全ての操作が杭 $0$ を経由しなければならないということです。このバージョンのパズルを最小回数の操作で解くアルゴリズムを説明してください。アルゴリズムが実行する操作は正確に何回ですか？
2. ♣ ❤ 杭 $0$ から杭 $2$、杭 $2$ から杭 $1$、杭 $1$ から杭 $0$ への操作だけが許されているとします。同じ条件を言い換えると、杭が環になっていて、反時計回りの操作だけが許されているということです。このバージョンのパズルを最小回数の操作で解くアルゴリズムを説明してください。アルゴリズムが実行する操作は正確に何回ですか？
  
  図 1.18
  
  反時計回りバージョンの Hanoi の塔問題の、解答の最初の数手
3. ♣ ❤ 最後に、杭 $0$ から杭 $2$ に円盤を動かせないとします。このバージョンのパズルを最小回数の操作で解くアルゴリズムを説明してください。アルゴリズムが実行する操作は正確に何回ですか？ [ヒント: 行列！このバージョンの解析は他の二つよりもはるかに難しいです。]
Hanoi の塔パズルの次の複雑な変種を考えます。$1$ から $k$ と名前の付いた杭が全部で $k$ 個あり、各操作で許されているのは任意の整数 $i$ について杭 $i$ にある一番小さい円盤を杭 $i - 1$ または $i + 1$ に移動させることだけです。通常の Hanoi の塔と同様に円盤はそれよりも小さい円盤の上に乗ることができません。パズルのゴールは $n$ 個の円盤を杭 $1$ から杭 $k$ に移動させることです。
1. $k = 3$ の場合の再帰的アルゴリズムを説明してください。アルゴリズムが実行する操作は正確に何回ですか？ (これは練習問題 1.4.(a) と全く同じ問題です)
2. $k = n + 1$ の場合の再帰的アルゴリズムで、操作が最大でも $O(n^{3})$ 回のものを説明してください。 [ヒント: (a) を使います。]
3. ❤ $k = n + 1$ の場合の再帰的アルゴリズムで、操作が最大でも $O(n^{2})$ 回のものを説明してください。[ヒント: (a) を使いません。]
4. ❤ $k = \sqrt{n}$ の場合の再帰的アルゴリズムで、操作が最大でも多項式回のものを説明してください。 (どんな多項式ですか？)
5. ❤ 任意の $n$ と $k$ に対する再帰的アルゴリズムを説明、解析してください。操作の回数が $n$ の多項式となるためには、$k$ は ($n$ の関数として) どの程度小さくないといけませんか？
${}$
再帰木
再帰木を使って次の再帰方程式を解いてください。 \[ \begin{aligned} A(n) &= 2 A(n/4) + \sqrt{n} & B(n) &= 2 B(n/4) + n & C(n) &= 2 C(n/4) + n^{2} \\ D(n) &= 3 C(n/3) + \sqrt{n} & E(n) &= 3 E(n/3) + n & F(n) &= 3 F(n/3) + n^{2} \\ G(n) &= 4 G(n/2) + \sqrt{n} & H(n) &= 4 H(n/2) + n & I(n) &= 4 I(n/2) + n^{2} \end{aligned} \]
再帰木を使って次の再帰方程式を解いてください。 \[ \begin{aligned} J(n) &= J(n/2) + J(n/3) + J(n/6) + n \\ K(n) &= K(n/2) + 2 K(n/3) + 3 K(n/4) + n^{2} \\ L(n) &= L(n/15) + L(n/10) + 2L(n/6) + \sqrt{n} \end{aligned} \]
❤ 再帰木を使って以下の再帰方程式を解いてください。 \[ \begin{aligned} M(n) &= 2 M(n/2) + O(n \log n) \\ N(n) &= 2 N(n/2) + O(n / \log n) \\ P(n) &= \sqrt{n}P(\sqrt{n}) + n \\ Q(n) &= \sqrt{2n} Q(\sqrt{2n}) + n \end{aligned} \]

${}$

ソート
直径が異なる $n$ 個のパンケーキが積み上がっている様子を想像してください。この状況から上から順に小さいパンケーキが並ぶように並び替えたいとします。ただし許されている動作はフリップ ――1 から $n$ の整数 $k$ について、上から $k$ 番目のパンケーキの下にへらを入れ、それより上にあるパンケーキを全てひっくり返す―― のみです。

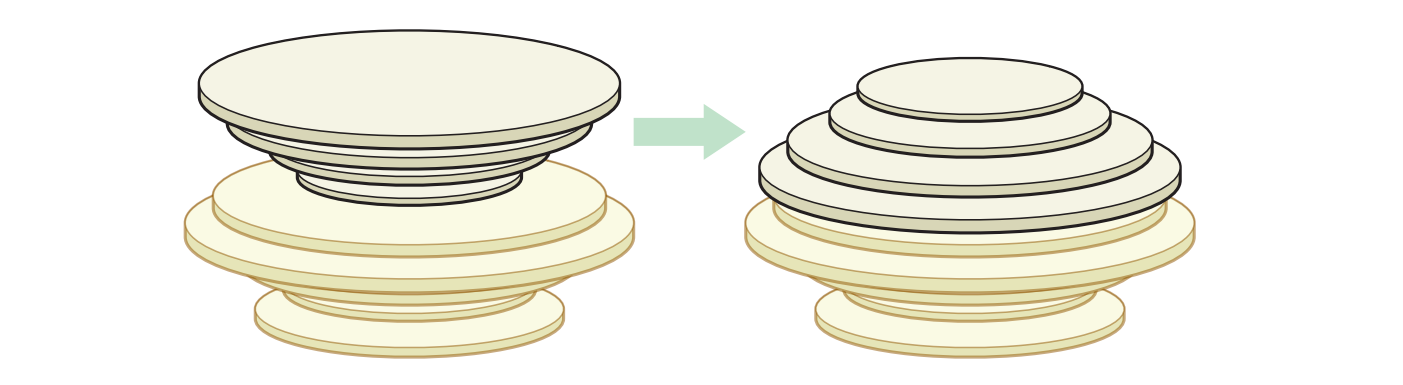図 1.19

4 つのパンケーキをフリップする
1. $n$ 個のパンケーキが任意に積みあがった状態から、$O(n)$ 回のフリップでソートを行うアルゴリズムを説明してください。最悪ケースでは正確に何回のフリップが必要になりますか⁴？ [ヒント: この問題はHanoi の塔とは関係がありません。]
2. $n$ を任意の正の整数として、ソートするのに $\Omega(n)$ 回のフリップが必要となる $n$ 個のパンケーキの積み上げ方を示してください。
3. 全てのパンケーキの片側に焼き目がついているとします。任意に積み上げられた $n$ 個のパンケーキを、焼き目がある面が全て下になるようにソートする $O(n)$ 回のフリップを求めるアルゴリズムを説明してください。最悪ケースでは正確に何回のフリップが必要になりますか？
クイックソートのピボット選択における「三つの中央値 (median of three)」ヒューリスティックとは、配列の最初、最後、中央の要素のうち中間のものをピボットとして選ぶというものです。三つの中央値ヒューリスティックが最悪ケースではソートに $\Omega(n^{2})$ 時間かかることを示してください。また任意の整数 $n$ について、三つの中央値クイックソートにおける全ての再帰呼び出しにおいて、ピボットが常に配列の中で二番目に小さい要素となるような 1 から $n$ までの整数の並び替えを示してください。並び替えを考える上では $\textsc{Partition}$ サブルーチンに関する深い知識が必要となります。
1. まずは準備運動として、$\textsc{Partition}$ サブルーチンが安定、つまりピボットよりも小さい要素の順番およびピボットよりも大きい要素の順番を保存するとして問題を解いてください。
2. ❤ $\textsc{Partition}$ が本文中にあるものだとして問題を解いてください。本文中の $\textsc{Partition}$ は安定ではありません。
1. Hey, Moe! Hey, Larry! このアルゴリズムが入力を正しくソートすることを示してくれ！
  
  procedure $\texttt{StoogeSort}$($ A[0..n-1] $)
  
  if $ n = 2 $ かつ $ A[0] > A[1] $ then
  
  swap $ A[0] \leftrightarrow A[1] $
  
  else if $ n > 2 $ then
  
  $ m = \lfloor 2n / 3 \rfloor $
  
  $\texttt{StoogeSort}$($ A[0..m-1] $)
  
  $\texttt{StoogeSort}$($ A[n-m..n-1] $)
  
  $\texttt{StoogeSort}$($ A[0..m-1] $)
2. $m = \lceil 2n / 3 \rceil$ の部分を $m = \lfloor 2n / 3 \rfloor$ にしたときに $\textsc{StoogeSort}$ が正しく動くかどうかを答え、それが正しいことを示してください。
3. $\textsc{StoogeSort}$ が実行するベースケースを含んだ比較演算の回数についての再帰方程式を示してください。
4. 再帰方程式を解いて、解が正しいことを証明してください。 [ヒント: 天井関数は無視できます。]
5. $\textsc{StoogeSort}$ で実行される swap の回数が最大 $\binom{n}{2}$ 回であることを示してください。
次の冷酷で異常な (cruel and unusual) ソートアルゴリズムは Gary Miller (ゲイリー・ミラー) によって提案されました。

このアルゴリズムで行われる比較演算の回数は入力の配列に依存していません。このようなソートアルゴリズムのことを無神経 (oblivious) であると言います。
1. $\textsc{Cruel}$ が入力の配列を正しくソートすることを帰納法で示してください。 [ヒント: 1, 2, 3, 4 を $n/4$ 個ずつ持つ長さ $n$ の配列を考えてください。なぜこれだけを考えれば十分なのでしょうか？]
2. $\textsc{Unusual}$ から for ループを取り除くと $\textsc{Cruel}$ が正しく動かなくなることを示してください。
3. $\textsc{Unusual}$ の最後の二行を交換すると $\textsc{Cruel}$ が正しく動かなくなることを示してください。
4. $\textsc{Unusual}$ の実行時間を求めて、それを証明してください。
5. $\textsc{Cruel}$ の実行時間を求めて、それを証明してください。
procedure $\texttt{Cruel}$($ A[1..n] $)

if $ n > 1 $ then

$\texttt{Cruel}$($ A[1..n/2] $)

$\texttt{Cruel}$($ A[n/2 + 1..n] $)

$\texttt{Unusual}$($ A[1..n] $)

procedure $\texttt{Unusual}$($A[1..n]$)

if $ n = 2 $ then

if $ A[1] > A[2] $ ⟨⟨唯一の比較！⟩⟩ then

swap $ A[1] \leftrightarrow A[2] $

else

⟨⟨$A$ を $4$ 分割して⟩⟩

⟨⟨$2$ 番目と $3$ 番目を入れ替える⟩⟩

for $ i \leftarrow 1 $ to $ n / 4 $ do

swap $ A[i + n/4] \leftrightarrow A[i + n/2] $

⟨⟨左半分に対する再帰⟩⟩

$\texttt{Unusual}$($ A[1..n/2] $)

⟨⟨右半分に対する再帰⟩⟩

$\texttt{Unusual}$($ A[n/2+1..n] $)

⟨⟨中央半分に対する再帰⟩⟩

$\texttt{Unusual}$($ A[n/4+1..n/4] $)
配列 $A[1..n]$ の転置 (inversion) とは、添え字の組 $(i, j)$ であって $i < j$ かつ $A[i] > A[j]$ を満たすものを言います。$n$ 要素の配列の転置の数は $0$ (配列がソートされているとき) から $\binom{n}{2}$ (配列が逆順にソートされているとき) までの値を取ります。$n$ 要素の配列を入力として受け取って、その配列の転置の数を $O(n \log n)$ 時間で計算するアルゴリズムを説明、解析してください。 [ヒント: マージソートを改変してください。]
1. 直線 $y=0$ 上の点 $\lbrace p_{1}, p_{2}, \ldots, p_{n} \rbrace$ と直線 $y=1$ 上の点 $\lbrace q_{1}, q_{2}, \ldots, q_{n} \rbrace$ が与えられたとします。$p_{i}$ と $q_{i}$ を結んで $n$ 本の直線を引いたときに、これらの直線が作る交点の数を $O(n\log n)$ 時間で求める分割統治アルゴリズムを説明、解析してください。 [ヒント: 前問と似ています。]
  
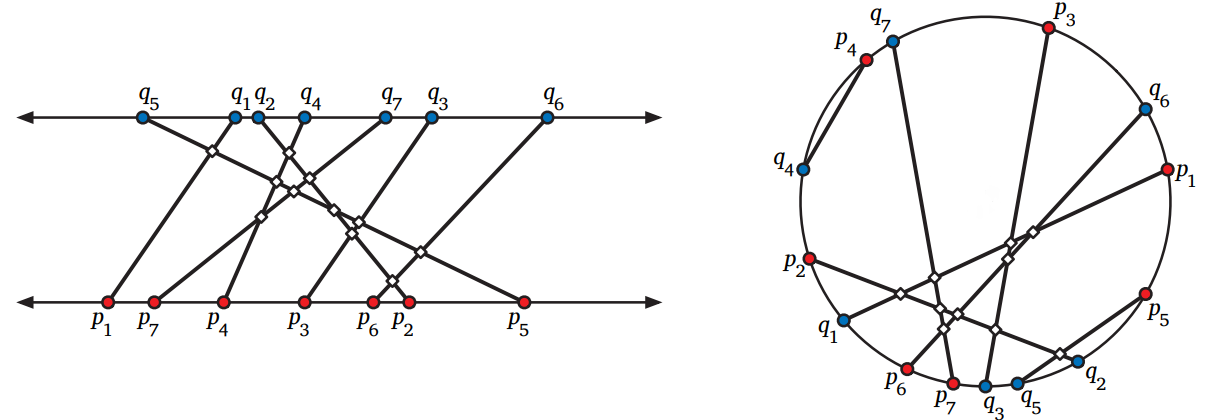  図 1.20
  
  平行な直線の間にかかった直線とそれによってできる 11 個の交点 (左)、および単位円周の中にかかった直線とそれによってできる 10 個の交点 (右)
2. 今度は $\lbrace p_{1}, p_{2}, \ldots, p_{n} \rbrace$ と $\lbrace q_{1}, q_{2}, \ldots, q_{n} \rbrace$ が単位円周上の点として与えられたとします。$p_{i}$ と $q_{i}$ を結んで $n$ 本の直線を引いたときに、これらの直線が作る交点の数を $O(n\log^{2} n)$ 時間で求める分割統治アルゴリズムを説明、解析してください。 [ヒント: (a) を使います。]
3. ❤ (b) で考えた問題に対する $O(n\log n)$ 時間のアルゴリズムを説明、解析してください。
1. 配列 $A[1..n]$ に対して、小配列 $A[k+1..k+\sqrt{n}]\ (k = 0 \ldots n - \sqrt{n})$ をソートするサブルーチンを $\textsc{SqrtSort}$ とします (簡単のために、ある整数 $k$ に対して $n = k^{2}$ とします)。この $\textsc{SqrtSort}$ サブルーチンだけを使って $n$ 要素の配列を正しくソートするアルゴリズムを説明してください。ただし、配列の検査、改変は必ず $\textsc{SqrtSort}$ を使って行わなければならず、要素を直接比較、移動、複製することは許されません。最悪ケースでは $\textsc{SqrtSort}$ は何回呼ばれますか？
2. ♣ (a) で答えたアルゴリズムが定数倍を無視すれば最適であることを示してください。つまり、アルゴリズムが $\textsc{SqrtSort}$ を呼ぶ回数を $f(n)$ としたときに、$\textsc{SqrtSort}$ を $o(f(n))$ 回使って配列をソートするアルゴリズムが存在しないことを示してください。
3. $\textsc{SqrtSort}$ が (a) の答えのアルゴリズムを使って再帰的に実装されているとします。例えば二段階目の再帰呼び出しでは、アルゴリズムの入力の長さは約 $n^{1 / 4}$ となります。このソートアルゴリズムの最悪計算時間を求めてください。(解析を簡単にするために、配列の大きさが $2^{2^{k}}$ という形であり、ルートの値がいつも整数であると仮定して構いません)。
${}$
選択
価値 (value) と重さ (weight) を持つ要素が $n$ 個入った集合 $S$ が与えられたとします。各 $x \in S$ に対して、次のように $S$ の部分集合を定義します。
- $S_{< x}$ は価値が $x$ の価値よりも小さい $S$ の要素からなる集合。
- $S_{> x}$ は価値が $x$ の価値よりも大きい $S$ の要素からなる集合。
$S$ の部分集合 $R \subseteq S$ に対して、$w(R)$ で $R$ の要素の重さの和を表すことにします。$S$ の重み付き中央値 (weighted median) とは、$S$ の要素 $x$ であって $w(S_{< x}) \leq w(S) / 2$ かつ $w(S_{> x}) \leq w(S) / 2$ を満たすものを言います。

重み付けされた要素が $n$ 個入った集合を受け取って、その集合の重み付き中央値を $O(n)$ 時間で計算するアルゴリズムを説明、解析してください。アルゴリズムの入力は二つの配列 $S[1..n]$ と $W[1..n]$ であり、添え字 $i$ について、$i$ 番目の要素は価値 $S[i]$ と重み $W[i]$ を持つとします。同じ価値を持つ要素は無く、重みは全て正であると仮定して構いません。
1. 入力として受け取った配列 $A[1..n]$ の中に同じ要素が $n/4$ 個以上あるかどうかを $O(n)$ 時間で判定するアルゴリズムを説明してください。
2. 入力として $A[1..n]$ と $k$ を受け取って、$A$ の中に同じ要素が $k$ 個以上あるかどうかを判定するアルゴリズムを説明、解析してください。アルゴリズムの実行時間を $n$ と $k$ の関数として表してください。
ハッシュソートや基数ソートなどの、入力の (順番ではなく) 値に依存するアルゴリズムを用いてはいけません。
配列 $A[1..5]$ が同じ要素を持たないときに、$A$ の中央値を最大 6 回の比較を使って求めるアルゴリズムを説明してください。説明には疑似コードではなくて決定木を使ってください。決定木は頂点が "$A[i] \lessgtr A[j]$" の形をしていて、葉が配列の添え字を表します。

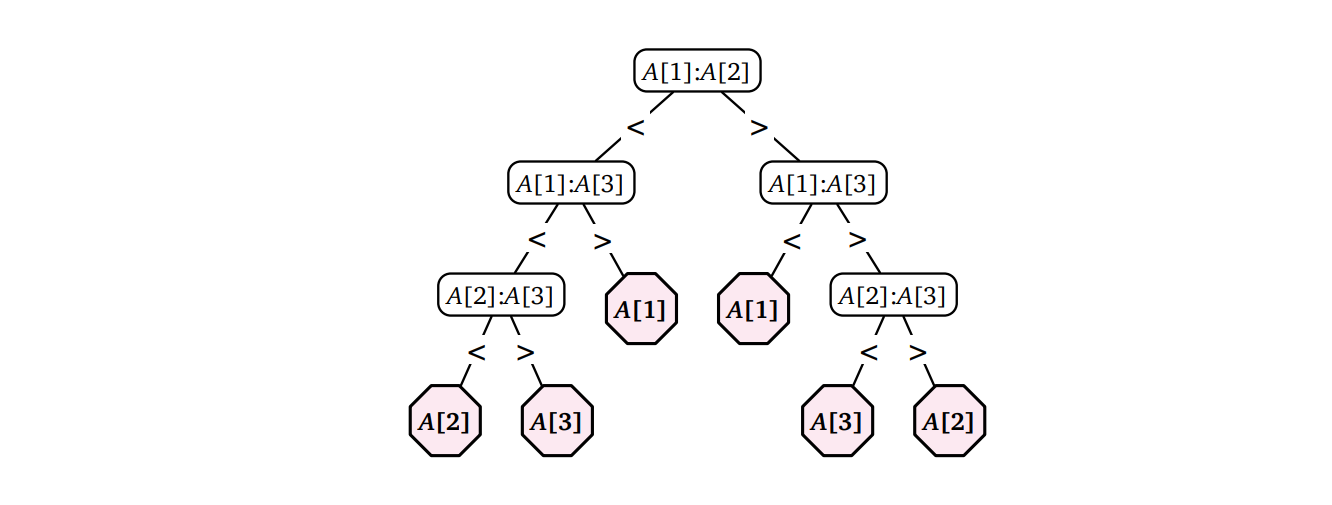図 1.21

三要素の配列の中央値を最大三回の比較を使って求める
次に示す、Blum-Floyd-Pratt-Rivest-Tarjan の $\textsc{MomSelect}$ アルゴリズムを一般化したものを考えます。このアルゴリズムは基本的に $\textsc{MomSelect}$ と同じですが、入力の配列を長さ 5 のブロック $\lceil n / 5 \rceil$ 個ではなく長さ $b$ のブロック $\lceil n/b \rceil$ 個に分割する点が異なります。
1. $b$ が定数だと仮定したとき ($\textsc{MedianOfB}$ が $O(1)$ 時間で実行されるとき) のアルゴリズムの実行時間に関する再帰方程式を示してください。再帰的に解く小問題の大きさは $b$ にどのように依存していますか？ $b$ が偶数の場合と奇数の場合を別々に考えること。
2. $\textsc{Mom1Select}$ の最悪計算時間を求めてください。 [ヒント: ひっかけ問題です。]
3. ♣ ❤ $\textsc{Mom2Select}$ の最悪計算時間を求めてください。 [ヒント: さらなるひっかけ問題です！]
4. ❤ $\textsc{Mom3Select}$ の最悪計算時間を求めてください。計算時間の上界はすぐに求まりますが、本当に難しいのはその解析が正しいと証明する部分です。 [ヒント: 練習問題 1.10]
5. ❤ $\textsc{Mom4Select}$ の最悪計算時間を求めてください。ここでも、難しいのは答えがこれ以上改善できないと示す部分です⁵。
6. 定数 $b \geq 5$ について、$\textsc{MomBSelect}$ の実行時間は $O(n)$ となります。しかし定数部分の値は $b$ によって異なります。
  
  $b$ 個の数字の中央値を計算するのに必要な比較演算の回数の最小値を $M(b)$ とすると、$M(b)$ の正確な値は $b \leq 13$ までしか知られていません。 \[ \begin{array}{r|rrrrrrrrrrrrr} b & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 \\ \hline M(b) & 0 & 1 & 3 & 4 & 6 & 8 & 10 & 12 & 14 & 16 & 18 & 20 & 23 \end{array} \]
  
  5 から 13 までの $b$ について、$\textsc{MomBSelect}$ の実行時間の上界を定数 $\alpha_{b}$ を使って $T(n) \leq \alpha_{b} n$ の形で求めてください (例えば本文中では $\alpha_{b} \leq 16n$ を示しました)。
7. $\alpha_{b}$ が最小となる $b$ を求めてください [ヒント: ひっかけ問題です！]
procedure $\texttt{MomBSelect}$($A[1..n], k$)

if $ n \leq \color{red}{b^{2}} $ then

総当たりで中央値を求める

else

$ m \leftarrow \color{red}{\lceil n / b \rceil} $

for $ i \leftarrow 1 $ to $m$ do

$ M[i] \leftarrow $$\texttt{MedianOfB}$($ \color{red}{A[b(i-1)+1..bi]} $)

$ \mathit{mom}_{\color{red}{b}} \leftarrow $$\texttt{MomBSelect}$($ M[1..m], \lfloor m/2 \rfloor $)

$ r \leftarrow $$\texttt{Partition}$($ A[1..n], \mathit{mom}_{\color{red}{b}} $)

if $k < r$ then

return $\texttt{MomBSelect}$($ A[1..r-1], k $)

else if $k > r$ then

return $\texttt{MomBSelect}$($ A[r+1..n], k-r $)

else

return $ \mathit{mom}_{\color{red}{b}} $

図 1.22

パラメータ化された選択アルゴリズムのクラス
次に示す Blum-Floyd-Pratt-Rivest-Tarjan の $\textsc{MomSelect}$ アルゴリズムの変種の実行時間が $O(n)$ であることを示してください。このアルゴリズムでは入力の配列に使うピボットを選ぶときの処理が一段階追加されています。

procedure $\texttt{MommomSelect}$($ A[1..n], k $)

if $ n \leq 81 $ then

総当たりで中央値を求める

else

$ m \leftarrow \lceil n / 3 \rceil $

for $ i \leftarrow 1 $ to $m$ do

$ M[i] \leftarrow $$\texttt{MedianOf3}$($ A[3i-2..3i] $)

$ mm \leftarrow \rceil m / 3 \rceil $

for $ j \leftarrow 1 $ to $mm$ do

$ \mathit{Mom}[j] \leftarrow $$\texttt{MedianOf3}$($ M[3j-2..3j] $)

$ \mathit{momom} \leftarrow $$\texttt{MomomSelect}$($ \mathit{Mom}[1..mm], \lfloor mm/2 \rfloor $)

$ r \leftarrow $$\texttt{Partition}$($ A[1..n], \mathit{momom} $)

if $k < r$ then

return $\texttt{MomomSelect}$($ A[1..r-1], k $)

else if $k > r$ then

return $\texttt{MomomSelect}$($ A[r+1..n], k-r $)

else

return $ \mathit{momom} $

図 1.23

mom の中央値を使った選択
1. 二つのソートされた配列 $A[1..n]$ と $B[1..n]$ が与えられたとき、$A$ と $B$ の和集合の中央値を $O(\log n)$ 時間で求めるアルゴリズムを説明してください。二つの配列には同じ要素が含まれないと仮定して構いません。
2. 二つのソートされた配列 $A[1..m]$ と $B[1..n]$ と整数 $k$ が与えられたときに、$A \cup B$ で $k$ 番目に小さい要素を $O(\log (m + n))$ 時間で求めるアルゴリズムを説明してください。例えば、$k = 1$ のとき、このアルゴリズムは $A \cup B$ の最小値を計算します。 [ヒント: (a) の答えを使います。]
3. ❤ 三つのソートされた配列 $A[1..n]$, $B[1..n]$, $C[1..n]$ と整数 $k$ が与えられたときに、$A \cup B \cup C$ から $k$ 番目に小さい整数を $O(\log n)$ 時間で求めるアルゴリズムを説明してください。
4. 最後に、二次元配列 $A[1..m,1..n]$ の各列 $A[i,\cdot]$ がソートされているときに、この二次元配列 $A$ と整数 $k$ を受け取って $A$ から $k$ 番目に小さい要素をできるだけ速く取り出すアルゴリズムを説明してください。アルゴリズムの実行時間は $m$ にどのように依存しますか？ [ヒント: 練習問題 1.16 を先に解いてください。]
${}$

算術
1854 年、1 から 59 までの整数の二乗が刻まれた紀元前 2000 年ごろのシュメールの粘土板が考古学者によって発見されました。この発見を持ってシュメール人が掛け算をするときには $x \cdot y = (x^{2} + y^{2} - (x-y)^{2}) / 2$ などの等式を用いた二乗への帰着が使われていたとする考古学者もいます。しかし残念ながら、そのような主張をする学者はシュメール人が大きな数字の二乗をどのように求めていたかについては口を閉ざしています。

粘土板が刻まれてから 4000年後の私たちは、再帰の力を使うことでシュメール人数学者を重労働から救うことができます！
1. Karatsuba のアルゴリズムを変更して、$n$ 桁の数の二乗の計算を、$\lceil n / 2 \rceil$ 桁の数の二乗の計算三つに帰着させることで $O(n^{\lg 3})$ 時間で行うアルゴリズムを作ってください (1960 年に Karatsuba がまさに行ったことです)。
2. $n$ 桁の数の二乗の計算を、$\lceil n / 3 \rceil$ 桁の数の二乗の計算六つに帰着させることで $O(n^{\log_{3} 6})$ 時間で計算するアルゴリズムを説明してください。
3. ❤ $n$ 桁の数の二乗の計算を、$(n/3 + O(1))$ 桁の二乗の計算五つに帰着させることで $O(n^{\log_{3} 5})$ 時間で計算するアルゴリズムを説明してください。 [ヒント: $(a + b + c)^{2} + (a - b + c)^{2}$ の値は何ですか？]
1. Karatsuba のアルゴリズムを変更して、$n \geq m$ のときに $m$ 桁の数と $n$ 桁の数の積を $O(nm^{\lg3 - 1})$ 時間で計算するアルゴリズムを作ってください。
2. $2^{n}$ の十進表記を $O(n^{\lg3})$ 時間で求めるアルゴリズムを (a) の答えをサブルーチンとして使って説明してください (答えを一桁ずつ計算する通常のアルゴリズムの実行時間は $\Theta(n^{2})$ です)。
3. $n$ 桁の二進数で表記された任意の数の十進表記を $O(n^{\lg 3})$ で求める分割統治アルゴリズムを説明してください。 [ヒント: 実行時間に追加される log の係数に注意してください。]
4. ❤ 二つの $n$ 桁の数の積を $O(M(n))$ 時間で計算できるとします。二進表記で $n$ 桁の任意の数の十進表記を $O(M(n) \log n)$ 時間で求めるアルゴリズムを説明してください。 [ヒント: 実行時間の解析は難しいです。定義域変換を使ってください。]
非負の整数 $n$ に対して階乗 $n!$ を計算する、次の古典的な再帰アルゴリズムを考えます。

procedure $\texttt{Factorial}$($n$)

if $n = 0$ then

return $1$

else

return $n \cdot {}$$\texttt{Factorial}$($n - 1$)
1. このアルゴリズムが行う乗算の回数を求めてください。
2. $n!$ を二進表記で書くために必要なビット数を求めてください。答えは適当な関数 $f(n)$ を使って $\Theta(f(n))$ の形で書いてください。 [ヒント: $(n/2)^{n/2} < n! < n^{n}$]
3. (b) の答えから、$\textsc{Factorial}$ の実行時間を乗算の数で測っても意味がないことが分かるでしょう。格子アルゴリズムまたは duplation と mediation のアルゴリズムを使えば、任意の $k$ 桁の数と $l$ 桁の数の積を $O(k \cdot l)$ 時間で計算できます。この乗算アルゴリズムをサブルーチンとして使ったときの $\textsc{Factorial}$ の実行時間を求めてください。
4. 次の再帰的なアルゴリズムも階乗を計算しますが、積の順番が異なります。
  
  ⟨⟨$n! / (n-m)!$ を計算する⟩⟩
  
  procedure $\texttt{Falling}$($n, m$)
  
  if $m = 0$ then
  
  return $1$
  
  else if $m = 1$ then
  
  return $n$
  
  else
  
  return $\texttt{Falling}$($n, \lfloor m / 2 \rfloor$) ${} \cdot {}$$\texttt{Falling}$($n - \lfloor m / 2 \rfloor, \lceil m / 2 \rceil$)
  
  小学校で使う掛け算アルゴリズムを使ったときの $\textsc{Falling}(n, n)$ の実行時間を求めてください。
5. Karatsuba のアルゴリズムを変更して、$k \geq l$ のときに $k$ 桁の数と $l$ 桁の数の積を $O(k \cdot l^{\lg 3 - 1}) \approx O(k \cdot l^{0.585})$ 時間で計算するアルゴリズムを説明、解析してください。
6. ❤ (e) で示した Karatsuba の乗算アルゴリズムを使ったときの $\textsc{Factorial}(n)$ および $\textsc{Falling}(n, n)$ の実行時間を求めてください。
正の整数 $x, y$ の最大公約数 (greatest common divisor) とは $x / d$ と $y / d$ がともに整数となる最大の整数 $d$ のことであり、$\gcd (x, y)$ と表記します。紀元前 300 年ごろに書かれた Euclid の『原論』では、$\gcd (x,y)$ を計算する次の再帰的アルゴリズムが説明されています⁶:

procedure $\texttt{EuclidGCD}$($x, y$)

if $x = y$ then

return $x$

else if $x > y$ then

return $\texttt{EuclidGCD}$($x - y, y$)

else

return $\texttt{EuclidGCD}$($x, y - x$)
1. $\textsc{EuclidGCD}$ が $\gcd (x, y)$ を正しく計算することを証明してください⁷。具体的には、次のことを示してください:
  - $\textsc{EuclidGCD}(x, y)$ が $x$ と $y$ を割り切ること
  - $x, y$ に共通する約数が $\textsc{EuclidGCD}(x, y)$ の約数であること
2. $\textsc{EuclidGCD}$ の最悪計算時間を $x, y$ の関数として求めてください ($x - y$ の計算には $O(\log x + \log y)$ 時間かかるとします)。
3. 次のアルゴリズムが $\gcd (x, y)$ を計算することを示してください。
  
  procedure $\texttt{FastEuclidGDC}$($x, y$)
  
  if $y = 0$ then
  
  return $x$
  
  else if $x > y$ then
  
  return $\texttt{FastEuclidGDC}$($y, x \text{ mod } y$)
  
  else
  
  return $\texttt{FastEuclidGDC}$($x, y \text{ mod } x$)
4. $\textsc{FastEuclidGCD}$ の最悪計算時間を $x, y$ の関数として求めてください ($x \text{ mod } y$ の計算には $O(\log x \cdot \log y)$ 時間かかるとします)。
5. 次のアルゴリズムが $\gcd (x, y)$ を計算することを示してください。
  
  procedure $\texttt{BinaryGCD}$($x, y$)
  
  if $x = y$ then
  
  return x
  
  else if $x$ と $y$ がどちらも偶数 then
  
  return $2 \cdot $$\texttt{BinaryGCD}$($x/2, y/2$)
  
  else if $x$ が偶数 then
  
  return $\texttt{BinaryGCD}$($x/2, y$)
  
  else if $y$ が偶数 then
  
  return $\texttt{BinaryGCD}$($x, y/2$)
  
  else if $x > y$ then
  
  return $\texttt{BinaryGCD}$($(x - y)/2, y$)
  
  else
  
  return $\texttt{BinaryGCD}$($x, (y - x)/2$)
6. $\textsc{BinaryGCD}$ の最悪計算時間を $x, y$ の関数として求めてください ($x - y$ の計算には $O(\log x + \log y)$ 時間、$z/2$ の計算には $O(\log z)$ 時間かかるとします)。
${}$

配列
$2^{n} \times 2^{n}$ の格子盤から (任意の位置の) マスを一つだけ取り除いたとします。この格子盤に三つのマスからなる L 字型のタイルを敷き詰める方法を計算するアルゴリズムを説明、解析してください。アルゴリズムの入力は整数 $n$ と穴の開いたマスの座標を表す $n$ ビットの整数二つであり、出力は $(4^{n} - 1)/3$ 個のタイルの座標と方向です。アルゴリズムの実行時間は $O(4^{n})$ としてください。 [ヒント: まずそのような敷き詰め方が常に存在することを示してください。]
$n$ 人の代議員の参加する政党大会 (あるいは教授会) に参加したとします。代議員はちょうど一つの政党に所属していますが、議員に所属政党を直接尋ねると大会からつまみ出されてしまうので、どの議員がどの政党に属しているかを見分けることはできません。しかし、二人の議員が同じ政党に属しているかどうかは見分けることができます。議員同士を対面させたときに、同じ政党の議員同士は必ず笑顔で握手を交わしながら挨拶するのに対して、異なる政党の議員同士は殺気立った目線と礼儀を欠いた態度で挨拶をするからです⁸。
1. 半分以上の代議員が同じ政党に所属している場合に、この政党の議員を全員特定する効率の良いアルゴリズムを説明してください。
2. 政党が三つ以上あり、その一つが最高得票数を持つ、つまり他の全ての政党よりも多く代議員を持つとします。この政党に所属する議員を極限まで少ない労力で特定する実践的な手続きを提示してください。最高得票数を持つ政党は少なくとも $p$ 人からなるとします。どうかお願いします。
Smullyan (スマリヤン) 島には三種類の住人がいます: 常に真実を話す騎士、常に嘘をつく悪党、そして真実を話すこともあれば嘘をつくこともある一般人です。島の住人はみな住民全員の名前と種類 (騎士、悪党、一般人) を知っています。あなたは住人全員の種類を知りたいとします。

島の住人に聞くことができるのは他の住人の種類だけです。つまり「X さん、こんにちは。Y の種類を教えてください」と尋ねることができ、答えは次のようになります:
- X が騎士なら、X は Y の正しい種類を答える。
- X が悪党なら、X は Y の正しい種類でない二つの種類のうちどちらかを答える。
- X が一般人なら、X は三つの種類の全てを答える可能性がある。
この形でない質問を島の住人にしても無視されます。したがって住人に自分自身の種類について聞くことはできません。また住人は同じ質問に対して同じ答えを返すので、同じ質問を何度も尋ねる意味はありません。
1. 住民の (狭義) 過半数が騎士であることを知っている場合に、住民全員の種類を決定する効率の良いアルゴリズムを説明してください。
2. 騎士が住民の過半数を占めていない場合には、住民全員の種類を決定できないことを示してください。
ほとんどのグラフィックスハードウェアでは blit (block transfer) と呼ばれる低レベル命令が利用できます。blit 命令とは四角形のピクセルマップ (ピクセルの値の二次元配列) のチャンクをコピーする命令であり、 C のライブラリ関数 memcpy() の二次元版と言うことができます。

$n \times n$ のピクセルマップを時計回りに $90^{\circ}$ 回転させたいとします。$n$ が $2$ のべきの場合には、ピクセルマップを四つの $n / 2 \times n / 2$ ブロックに分け、各ブロックを五回の blit 命令で正しい位置に移動させ、それぞれのブロックを再帰的に回転させることで回転を行うことができます (blit 命令が五回なのは、Hanoi の塔パズルが杭を三つ必要としたのと同じ理由です)。あるいは、最初に再帰的に回転させてから blit で正しい位置に移動させるということもできます。

図 1.24

ピクセルマップを回転させる二つのアルゴリズム
1. $n$ が $2$ のべきのときに、両方のバージョンのアルゴリズムが正しいことを証明してください。
2. $n$ が $2$ のべきのときに、blit 命令が実行される回数を求めてください。
3. $2$ のべきではない任意の $n$ についても正しく実行されるようにはアルゴリズムをどう改変すればよいか説明してください。改変されたアルゴリズムにおいて blit は何回実行されますか？
4. $k \times k$ の blit 命令の実行時間が $O(k^{2})$ である場合、(c) で答えたアルゴリズムの実行時間を求めてください。
5. $k \times k$ の blit 命令の実行時間が $O(k)$ の場合はどうなりますか？⁹
異なる $n$ 個の要素からなる配列 $A[0..n-1]$ がバイトニック(bitonic) であるとは、添え字の組 $i, j$ であって $A[(i - 1) \text{ mod } n] <$ $A[i] > A[(i + 1) \text{ mod } n]$ かつ $A[(j - 1) \text{ mod } n] >$ $A[j] < A[(j + 1) \text{ mod } n]$ を満たすものがちょうど一つ存在することを言います。言い換えると、要素を最初からたどっていったときに最初は順に大きくなり、ある要素からは順に小さくなる配列、または環状にシフトするとそのような配列になる配列がバイトニックな配列です。例えば:
- $[4\ 6\ 9\ 8\ 7\ 5\ 1\ 2\ 3]$ はバイトニックです。
- $[3\ 6\ 9\ 8\ 7\ 5\ 1\ 2\ 4]$ はバイトニックではありません。
バイトニックな長さ $n$ の配列から最小要素を $O(\log n)$ 時間で取り出すアルゴリズムを説明、解析してください。入力配列に入っている数には重複がないことを仮定して構いません。
異なる $n$ 個の整数からなるソートされた配列 $A[1..n]$ が与えられたとします。$A$ の要素は負またはゼロまたは正の整数であり、$A[1] < A[2] < \cdots < A[n]$ とソートされているとします。
1. $A[i] = i$ を満たす添え字 $i$ が存在するなら $i$ を計算し、存在しないならそのことを答える高速なアルゴリズムを説明してください。
2. $A[1] > 0$ であることが事前にわかっているとします。$A[i] = i$ を満たす添え字 $i$ が存在するなら $i$ を計算し、存在しないならそのことを答える高速なアルゴリズムを説明してください。 [ヒント: この問題は超簡単です。]
配列 $A[1..n]$ が $A[1] \geq A[2]$ と $A[n-1] \leq A[n]$ を満たしているとします。要素 $A[x]$ が極小であるとは、$A[x]$ の隣の要素が両方とも $A[x]$ より大きいことを言います。きちんと言うと、$A[x - 1] \geq A[x]$ かつ $A[x] \leq A[x + 1]$ だということです。例えば次の配列には六つの極小値があります: \[ 9\ {\color{#B52F1B}{7}}\ 7\ 2\ {\color{#B52F1B}{1}}\ 3\ 7\ 5\ {\color{#B52F1B}{4}}\ 7\ {\color{#B52F1B}{3}}\ {\color{#B52F1B}{3}}\ 4\ 8\ {\color{#B52F1B}{6}}\ 9 \] 配列を順番に探索すれば極小値の一つを $O(n)$ 時間で見つけることができるのは明らかです。極小値の一つを $O(\log n)$ 時間で求めるアルゴリズムを説明、解析してください。 [ヒント: 与えられた境界条件の下では配列には少なくとも一つの極小値が含まれます。なぜでしょうか？]
ソートされた長さ $n$ の配列を $k\ (= 1 \ldots n - 1)$ 回シフトしたものが与えられたとします。つまり、最初の部分 $A[1..k]$ は昇順に、後ろの部分 $A[k+1..n]$ は降順にソートされていて、かつ $A[n] < A[1]$ だということです。ここで $k$ は未知数です。

例えば、次の 16 要素の配列が与えられます ($k = 10$ です): \[ 9\ 13\ 16\ 18\ 19\ 23\ 28\ 31\ 37\ 42\ |\ 1\ 3\ 4\ 5\ 7\ 8 \]
1. 未知の整数 $k$ を求めるアルゴリズムを説明、解析してください。
2. 入力として受け取る $x$ が $A$ に含まれるかどうかを判定するアルゴリズムを説明、解析してください。
大ヒットアクション映画 Fast and Impossible XIII $\frac{3}{4}$: The Last Guardians of Expendable Justice Reloaded の第二幕の終盤で、悪役の Dr. Metaphor がヒーロー全員に催眠術をかけるシーンがあります。その上で Dr. Metaphor はヒーローたちを崖際に一列に並ばせ、合図とともに自分の右および左にいるヒーローの中で、一番近くにいる自分よりも背が高いヒーローを両方銃で撃つように命じました。

$n$ 人のヒーローの背の高さが左から右に $\mathit{Ht}[1..n]$ で与えられるとします (給料の支払いで揉めないように、プロデューサーは同じ背の高さのヒーローを雇いませんでした)。次の総当たりアルゴリズムを使えば、各ヒーローの左右の標的を $O(n^{2})$ 時間で求めることができます:

procedure $\texttt{WhoTargetsWhom}$($\mathit{Ht}[1..n]$)

for $j \leftarrow 1$ to n do

⟨⟨ヒーロー $j$ の左の標的 $L[j]$ を求める⟩⟩

$L[j] \leftarrow \textsc{None}$

for $i \leftarrow 1 $ to $j - 1$ do

if $\mathit{Ht}[i] > \mathit{Ht}[j]$ then

$L[j] \leftarrow i$

⟨⟨ヒーロー $j$ の右の標的 $R[j]$ を求める⟩⟩

$R[j] \leftarrow \textsc{None}$

for $k \leftarrow n $ downto $j + 1$ do

if $\mathit{Ht}[k] > \mathit{Ht}[j]$ then

$R[j] \leftarrow k$

return $L[1..n],\ R[1..n]$
1. $\textsc{WhoTargetsWhom}$ の出力を $O(n \log n)$ 時間で計算する分割統治アルゴリズムを説明してください。
2. $n$ 人のヒーローのうち少なくとも $\lfloor n / 2 \rfloor$ 人が誰かの標的になることを示してください。つまり、出力の配列 $R[0..n-1]$ と $L[0..n-1]$ の中には ($\textsc{None}$ でない) 異なる値が少なくとも $\lfloor n / 2 \rfloor$ 個含まれることを示してください。
3. あぁ、なんということでしょう。Dr. Metaphor の極悪非道な計画は実行されました。合図とともに全てのヒーローは標的に向かって銃を撃ち、打たれたヒーローは崖から落ちていきました。助からないでしょう。さらに、この卑劣な実験は何度も繰り返されました。Dr. Metaphor は殺戮が終わるたびに生き残ったヒーローたちに新しい標的を選ばせ、合図を送って銃を撃たせました。そうして、最終的には背が一番低いヒーローが生き残りました¹⁰。
  
  シーンが終了するまでに Dr. Metaphor が合図を鳴らす回数を計算するアルゴリズムを説明、解析してください。満点を得るためには、アルゴリズムの実行時間が $O(n)$ であることが求められます。
あなたは人気テレビ番組 "お隣さんを倒せ！" に参加しました。あなたの前には $m \times n$ の格子があって、各マスには異なる番号が書かれています。このゲームの目標は上下左右のマスよりも大きな値を持つマスを見つけることであり、一つのマスの値を確認するには $100 かかります。対戦相手よりも少ない金額でそのようなマスを見つければ勝ちで、ラスベガスへのペア旅行券と、誰もが喉から手が出るほど欲しがっている Rice-A-Roni™ 一年分を獲得できます。
1. $m = 1$ とします。左右のマスよりも値が大きいマスを見つけるアルゴリズムを説明してください。最悪ケースではマスをいくつ開けることになりますか？
2. ❤ $m = n$ とします。上下左右のマスよりも値が大きいマスを見つけるアルゴリズムを説明してください。最悪ケースではマスをいくつ開けることになりますか？
3. ♣ ❤ (b) の答えが定数倍を無視すれば最良であることを証明してください。
1. $l$ を正の整数とします。$n = 2^{l} - 1$ として、異なる $l$ ビットバイナリ文字列の配列 $A[1..n]$ が与えられたとします。つまり、ちょうど一つの $l$ ビットバイナリ文字列が $A$ に含まれていないということです。$A$ にアクセスする方法が $A[i]$ の第 $j$ ビットを $O(1)$ 時間で取得する関数 $\textsc{FetchBit}(i, j)$ だけに限られているとしたとき、$A$ に含まれない唯一の文字列を $O(n)$ 回の $\textsc{FetchBit}$ の呼び出しで見つけるアルゴリズムを説明してください。
2. $k, l$ を正の整数として $n = 2^{l} - k$ とします。そして前問と同じように $A[1..n]$ に異なる $l$ ビットバイナリ文字列が入っているとします。 $A$ に入っていない $k$ 個の文字列を $O(n \log k)$ 回の $\textsc{FetchBit}$ の呼び出しで見つけるアルゴリズムを説明してください。
${}$

木
この問題では、二分木に含まれる任意の連結部分グラフを部分木と呼びます。二分木が完全であるとは、全ての葉でない頂点がちょうど二つの子を持ち、全ての葉が同じ深さを持つことを言います。与えられた二分木に含まれる最大完全部分木を計算する再帰的なアルゴリズムを説明、解析してください。アルゴリズムの出力は部分木の根と深さです。次の図に例を示します。

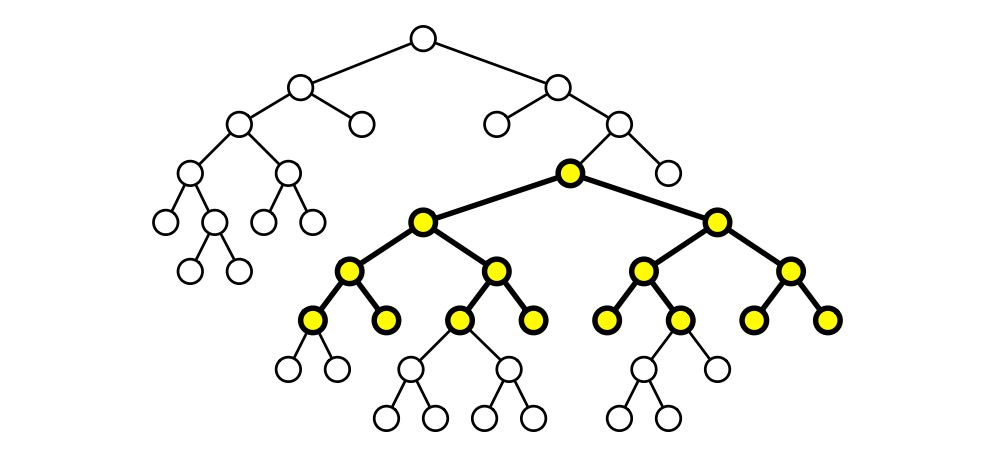$この二分木の最大完全部分木の高さは $3$$

図 1.26

この二分木の最大完全部分木の高さは $3$
$T$ を $n$ 頂点の二分木とします。 $T$ から頂点 $v$ を取り除くと最大で三つの部分木が生じます。つまり、左の子を含む部分木、右の子を含む部分木、そして親を含む部分木です。頂点 $v$ が中心であるとは、$v$ を取り除くことによって生じる部分木がどれも $n / 2$ 以下の頂点しか持たないことを言います。次の図に例を示します。

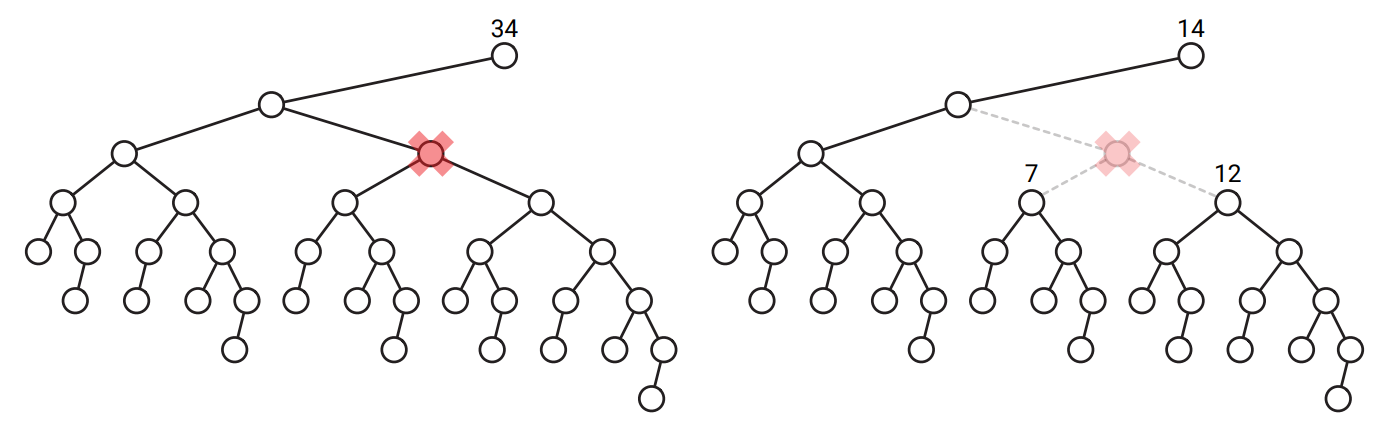$$34$ 頂点の二分木から中心の頂点を取り除くと、頂点数が $14$, $7$, $12$ の部分木が残る$

図 1.27

$34$ 頂点の二分木から中心の頂点を取り除くと、頂点数が $14$, $7$, $12$ の部分木が残る

任意の二分木を受け取ってその中心の頂点を見つけるアルゴリズムを説明、解析してください。 [ヒント: まずどんな木にも中心があることを示してください。]
1. George O'Jungle 教授はある二分木を持っています。その二分木には頂点が 27 個あり、各頂点がアルファベットおよび "&" でユニークにラベル付けされています。行きがけ順 (preorder) および帰りがけ順 (postorder) でこの二分木を走査すると、頂点が次の順番に並ぶそうです:
  - 行きがけ順: I Q J H L E M V O T S B R G Y Z K C A & F P N U D W X
  - 帰りがけ順: H E M L J V Q S G Y R Z B T C P U D N F W & X A K O I
  教授の持っている二分木を復元してください。
2. 全二分木 (full binary tree) とは全ての葉でない頂点が二つの子を持つ二分木のことです。
  1. 任意の全二分木の行きがけ順および帰りがけ順の走査結果からを元の全二分木を復元する再帰的なアルゴリズムを説明、解析してください。
  2. 任意の二分木の行きがけ順および帰りがけ順の走査結果からを元の二分木を復元するアルゴリズムが存在しないことを示してください。
3. 任意の二分木の行きがけ順および通り掛け順 (inorder) の走査結果から元の二分木を復元するアルゴリズムを説明、解析してください。
4. 任意の二分探索木の行きがけ順の走査結果だけを使って、元の二分探索木を復元するアルゴリズムを説明、解析してください。
5. ❤ 任意の二分探索木の行きがけ順の走査結果だけを使って、元の二分探索木を $\pmb{O(n)}$ 時間で復元するアルゴリズムを説明、解析してください。
(b) - (e) では、二分木のキーは全て異なっていて、入力は少なくとも一つの二分木を表していると仮定して構いません。
二次元の領域内に $n$ 個の点が与えられたとします。kd-木 (kd-tree) はこれらの点を次のように再帰的に分割します。まず領域の内部に点が無いならば、それで終わりです。そうでないなら、点の一つを通る垂直な直線によって点の数がなるべく等しくなるように領域を二つに分けます。その後領域を 90 度回転させてから、再帰的に分割を行います。これによって、垂直方向と水平方向の分割が交互に起きます。最後に残る空領域のことをセル (cell) と言います。

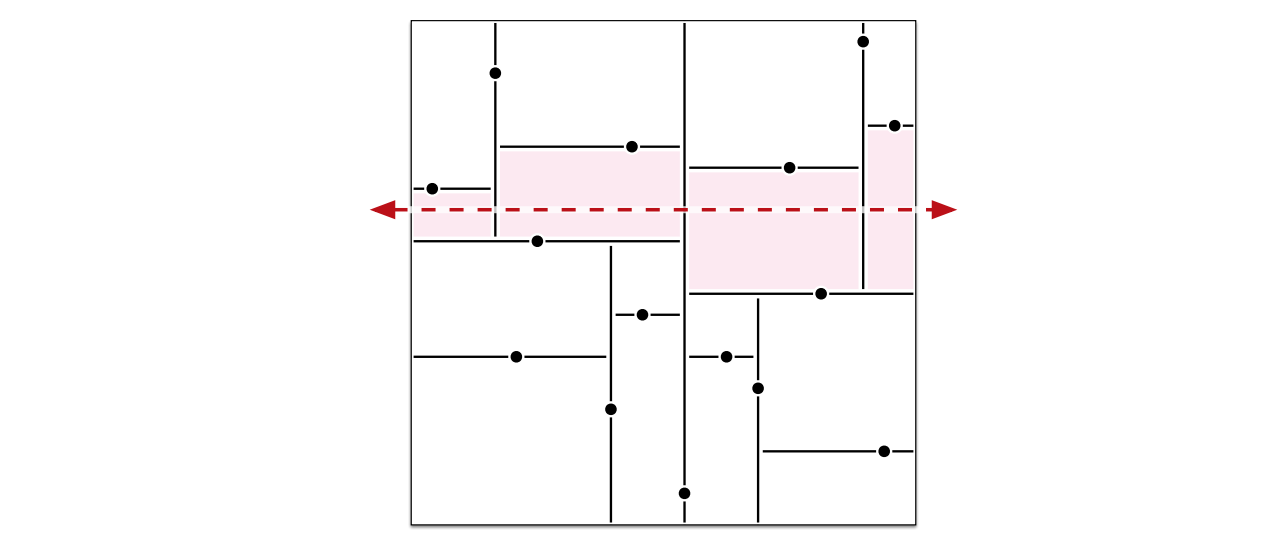図 1.28

15 個の点に対する kd-木、点線は色のついた4つのセルを通る
1. セルの個数を $n$ の関数として求めて、それが正しいことを証明してください。
2. 領域を通過する水平な直線が通るセルの個数の最悪ケースにおける正確な値を $n$ の関数として求めてください。適当な整数 $k$ を使って $n = 2^{k} - 1$ と表せると仮定して構いません。 [ヒント: $f(16) = 4$ となるような関数は二つ以上あります。]
3. kd-木に保存された $n$ 点が与えられたときに、ある水平線よりも上にある点の数をなるべく速く計算するアルゴリズムを説明、解析してください。 [ヒント: (b) を使います。]
4. kd-木に保存された $n$ 点が与えられたときに、垂直および水平な辺からなる長方形 $R$ に含まれる点の数を計算する効率の良いアルゴリズムを説明、解析してください。 [ヒント: (c) を使います。]
❤ CS225 の新入生 Bob Ratenbur は二分木の行きがけ順 (preorder)、通り掛け順 (inorder)、帰りがけ順 (postorder) の走査を行おうとしています。Bob は走査アルゴリズムの基本的な考えをなんとなく理解したのですが、実際に走査を実装するときになって再帰呼び出しをどのように行えばいいかが分からなくなってしまいました。締め切りの 5 分前、Bob は必死になって次のコードを書き上げて提出しました:

procedure $\texttt{PreOrder}$($v$)

if $v == \textsc{Null}$ then

return

else

print $\mathit{label}(v)$

$\blacksquare \blacksquare \blacksquare$$\texttt{Order}$($\mathit{left}(v)$)

$\blacksquare \blacksquare \blacksquare$$\texttt{Order}$($\mathit{right}(v)$)

procedure $\texttt{InOrder}$($v$)

if $v == \textsc{Null}$ then

return

else

$\blacksquare \blacksquare \blacksquare$$\texttt{Order}$($\mathit{left}(v)$)

print $\mathit{label}(v)$

$\blacksquare \blacksquare \blacksquare$$\texttt{Order}$($\mathit{right}(v)$)

procedure $\texttt{PostOrder}$($v$)

if $v == \textsc{Null}$ then

return

else

$\blacksquare \blacksquare \blacksquare$$\texttt{Order}$($\mathit{left}(v)$)

$\blacksquare \blacksquare \blacksquare$$\texttt{Order}$($\mathit{right}(v)$)

print $\mathit{label}(v)$

疑似コードの $\blacksquare \blacksquare \blacksquare$ の部分には接頭語 $\textsc{Pre}, {}$$\textsc{In}, {}$$\textsc{Post}$ のどれかが入ります。さらに Bob が提出したコードには次の関数がちょうど一回ずつ含まれています:
- $\textsc{PreOrder}(\mathit{left}(v)), {}$ $\textsc{PreOrder}(\mathit{right}(v))$
- $\textsc{InOrder}(\mathit{left}(v)), {}$ $\textsc{InOrder}(\mathit{right}(v))$
- $\textsc{PostOrder}(\mathit{left}(v)), {}$ $\textsc{PostOrder}(\mathit{right}(v))$
Bob のコードには 36 通りの可能性があります。不幸なことに、Bob は実行可能形式を提出した後に間違ってソースコードを削除してしまいました。そのため彼にもあなたにもどの関数がどこで呼ばれているかは分かりません。

この条件の下で、未知の二分木 $T$ に対して実行された Bob の走査アルゴリズムの出力を配列 $\mathit{Pre}[1..n], \mathit{In}[1..n], \mathit{Post}[1..n]$ に収めることができたとします。これらの配列が一つの二分木 $T$ に対する出力であること、$T$ の頂点ラベルに重複が無いこと、$T$ の葉でない頂点が必ず二つの子を持つことを仮定して構いません。
1. 走査結果から未知の二分木 $T$ を復元するアルゴリズムを説明してください。
2. 走査結果から Bob のコードを復元するか、走査の結果と矛盾しないコードが複数あるので復元できないことを正しく報告するアルゴリズムを説明してください。
例えば、入力 \[ \begin{aligned} \mathit{Pre}[1..n] & = [H A E C B I F G D] \\ \mathit{In}[1..n] & = [A H D C E I F B G] \\ \mathit{Post}[1..n] & = [A E I B F C D G H] \end{aligned} \] に対して、(a) のアルゴリズムは次の木を返します:

(b) のアルゴリズムは次のコードを復元します:

procedure $\texttt{PreOrder}$($v$)

if $v == \textsc{Null}$ then

return

else

print $\mathit{label}(v)$

$\texttt{PreOrder}$($\mathit{left}(v)$)

$\texttt{PostOrder}$($\mathit{right}(v)$)

procedure $\texttt{InOrder}$($v$)

if $v == \textsc{Null}$ then

return

else

$\texttt{PostOrder}$($\mathit{left}(v)$)

print $\mathit{label}(v)$

$\texttt{PreOrder}$($\mathit{right}(v)$)

procedure $\texttt{PostOrder}$($v$)

if $v == \textsc{Null}$ then

return

else

$\texttt{InOrder}$($\mathit{left}(v)$)

$\texttt{InOrder}$($\mathit{right}(v)$)

print $\mathit{label}(v)$
❤ 頂点に数値が保存されている二分木を $T$ とします。 $T$ が二分探索木であるとは (1) $T$ が空である、または (2) $T$ が次の再帰的条件:
- $T$ の左の部分木が二分探索木である。
- 左の部分木にある頂点の値は全て $T$ の根の値より小さい。
- $T$ の右の部分木が二分探索木である。
- 右の部分木にある頂点の値は全て $T$ の根の値より大きい。
を満たすことを言います。

二分木に対する次の二つの操作を考えます:
- 任意の頂点を上に回転 (rotate) させる¹¹。
- 任意の頂点に対して、左右の部分木のスワップ (swap) を行う。
両方の操作において、部分木 $A, B, C$ のいずれかあるいは全てが空でも構いません。
1. $n$ 個の頂点の値に重複がない任意の二分木を受け取って、$O(n^{2})$ 回の rotate と swap でその木を二分探索木に変形させるアルゴリズムを説明してください。五つの頂点を持つ二分木を八回の操作で二分探索木に変形する様子を次に示します。
  
  図 1.29
  
  二分木の「ソート」: rotate 2, rotate 2, swap 3, rotate 3, rotate 4, swap 3, rotate 2, swap 4
  
  答えのアルゴリズムでは親や子のポインタを直接変更したり、新しく頂点を作ったり、元からある頂点を削除することは許されません。木の変更は rotate と swap を使うことでのみ行えます。
  
  一方で木を変更しないなら、何かを計算するのはタダで行えます。アルゴリズムの実行時間は rotate と swap 操作の回数であると定義されているからです。
2. ❤ $n$ 個の頂点を持つ任意の二分木を $O(n \log n)$ 回の rotate と swap で二分探索木に変形するアルゴリズムを説明してください。
3. 任意の二分探索木は $O(n)$ 回の rotate (swap は使わない) で頂点の値が同じ別の二分探索木に変形できることを示してください。
4. ❤ 未解決問題: $n$ 個の頂点を持つ任意の二分木を $O(n)$ 回の rotate と swap で二分探索木に変形するアルゴリズムを示すか、そのようなアルゴリズムは存在しないことを示してください。 [ヒント: 私はこのような変形が可能だとは思いません。]

De Viribus Quantitatis (『数字の力について』) は初期の娯楽数学に関する重要な著作であり、おそらくは魔法に関する現存最古の著作でもあります。Pacioli は Summa de Arithmetica の著者としての方がよく知られています。これは十五世紀数学のほぼ完全な百科事典であり、複式簿記が説明された最初の書籍です。^[return]
baguenaudier-jeu by EN NOIR & BLANC (CC0 1.0) . 訳注: 英語版とは異なる図を使っています。^[return]
この話には真実が部分的に含まれます。^[return]
最悪ケースにおいて $n$ 個のパンケーキをソートする最適なフリップの正確な値を求める問題は (焼き目の有無に関わらず) 長い間未解決です。できるだけのことをやってみてください。^[return]
4つの要素の中央値は二番目に大きい要素または二番目に小さい要素です。Ke Chen と Adrian Dumitrescu が2014 年に証明したことによると、$k < n / 2$ のときは二番目に小さい要素を、$k > n/2$ のときは二番目に大きい要素を選ぶと、アルゴリズムの実行時間が $O(n)$ となります！詳細は "Select with Groups of 3 or 4 Takes Linear Time" (WADS 2015, arXiv:1409.3600) を見てください。^[return]
Euclid のアルゴリズムが最古の再帰的アルゴリズムである、あるいは最古の自明でないアルゴリズムであると説明されることがありますが、これは間違っています。エジプト人の duplation と mediation を使った乗算アルゴリズムは再帰的であり、自明でもありませんが、Euclid よりも少なくとも 1500 年前に使われています。^[return]
Euclid はこれを示していません。『原論』の第四巻の命題 1 は「$\textsc{EuclidGCD}(x,y) = 1$ ならば $x$ と $y$ は互いに素 ($\gcd (x, y) = 1$)」ですが、その証明は $x \text{ mod } (y \text{ mod } (x \text{ mod } y))= 1$ という特殊な場合しか考えていません。また命題 2 は「$x$ と $y$ が互いに素でないならば $\textsc{EuclidGCD}(x, y) = \gcd (x, y)$」ですが、その証明は $\gcd (x, y) = y$ と $\gcd (x, y) = y \text{ mod } (x \text{ mod } y)$ という場合しか考えていません。さらに言えば、この二つの命題が正しくても $\textsc{EuclidGCD}$ の正しさは証明できません。Euclid のようにならないでください。^[return]
現実の政治はもっと複雑ですが、これは理論の本です！^[return]
訳注: 英語版ではこの後に画像がありますが、権利の都合でコピーできませんでした。^[return]
スリル満点の最終章 Retcon the Squirrel では、最後まで生き残ったヒーローがタイムトラベルして事前に $n - 1$ 人のヒーローを本物そっくりの風船人形に入れ替えることでヒーロー全員を救います。えぇ、そうです。これが Avengers: Endgame のあらすじです。^[return]
rotate は二分木の行きがけ順を保存します。そのため二分探索木の中にはバランスを保つのに rotate 操作を使うものがあります。例えば AVL 木、赤黒木、スプレー木、スケープゴート木、treap などです。これらのデータ構造は http://algorithms.wtf にある講義ノートで解説されています。^[return]