最短路

私はリンゴを収穫するように聖書を研究する。最初に木全体をゆすってみる。そうすれば、最も熟れた実が落ちるかもしれない。それから私は木に登って大枝をゆすり、枝をゆすり、小枝をゆすり、そして葉の下を覗く。

――Martin Luther (c. 1500)

人生は一歩ずつ広がる。遠くに進めばそれだけ、多くの真実を理解できるようになる。

我々の足元にあるものを理解することが、その先にあるものを理解するための一番の準備である。

――Hypatia of Alexandria (c. 400), Elbert Hubbard 著 Little Journeys to the Homes of Great Teachers (1908) より

リラックスすることを覚えたなら、あとは答えを待っていればほとんどの問題はあなたの頭が答えてくれる。

そこらにある思考機械と同じように、問題を入れたら、椅子に深く座って、待つ...

――William S. Burroughs, Naked Lunch (1959)

この論文で示される手続きは何の洞察も創意工夫も必要としない。

ゆえに、この手続きはアルゴリズムと言える。

――Edward R. Moore, "The Shortest Path Through a Maze" (1959)

重み付きの有向グラフ \(G = (V, E, w)\) に加えてソース頂点 (source vertex) \(s\) と目標頂点 (target vertex) \(t\) という二つの特別な頂点が与えられ、\(s\) から \(t\) への最短路を見つけたいとします。つまり、\(s\) から \(t\) への路 \(P\) であって次の関数を最小化するものです: \[ W(P) := \sum_{u \rightarrow v \in P} w(u \rightarrow v) \]

例えば「私が昔住んでいたイリノイ州シャンペーンの家から私の妻が昔住んでいたオハイオ州コロンバスの家まで車で行く場合の最短経路は？」という問題の答えを知りたい場合は、頂点が都市に、辺が道路に、辺の重みがその道路の運転時間に対応するグラフを使って、\(s\) をシャンペーンに、\(t\) をコロンバスとして最短路問題を解くことになります¹。同じ道路でも方向によって運転時間が異なることがあるのに対応して、グラフは有向です (あるときインディアナ州とオハイオ州の州境のすぐ東の I-70 道路にネズミ捕りが仕掛けられていたのですが、東へ向かう道路にしか仕掛けられていませんでした)。

最短路木

ある頂点から別の頂点への最短路を計算するほとんど全てのアルゴリズムが実際に解いているのは、次に説明する単一ソース最短路 (single source shortest path, SSSP) 問題です。これは \(s\) からグラフに含まれる他の全ての頂点への最短路を求める問題であり、通常は \(s\) を根とする最短路木 (shortest path tree) を見つけることで解かれます。最短路木には求めるべき全ての最短路が含まれます。

各頂点への最短路がユニークならばそれらの最短路を合わせると木になるというのはすぐに分かります。このような場合には、最短路の任意の部分路もまた最短路となるためです。またいずれかの頂点に対する最短路が複数ある場合でも、全ての頂点への最短路の和集合が木になるように各頂点への最短路を必ず選ぶことできます。つまり、もし \(s\) から \(u\) への最短路と \(s\) から \(v\) への最短路が最初の部分で一致していて、途中で離れ、最後にまた一致するようになっている場合には、路を改変することで二つの最短路が一度だけ一致するようにできます。

図 8.1

もし \(s \rightarrow a\) \(\rightarrow b\) \(\rightarrow c\) \(\rightarrow d\) \(\rightarrow v\) (実線) と \(s \rightarrow\) \(a \rightarrow\) \(x \rightarrow\) \(y \rightarrow\) \(d \rightarrow u\) (破線) が最短路なら、\(s \rightarrow a\) \(\rightarrow b\) \(\rightarrow c\) \(\rightarrow d\) \(\rightarrow u\) (上側の頂点だけを通る路) もまた最短路である。

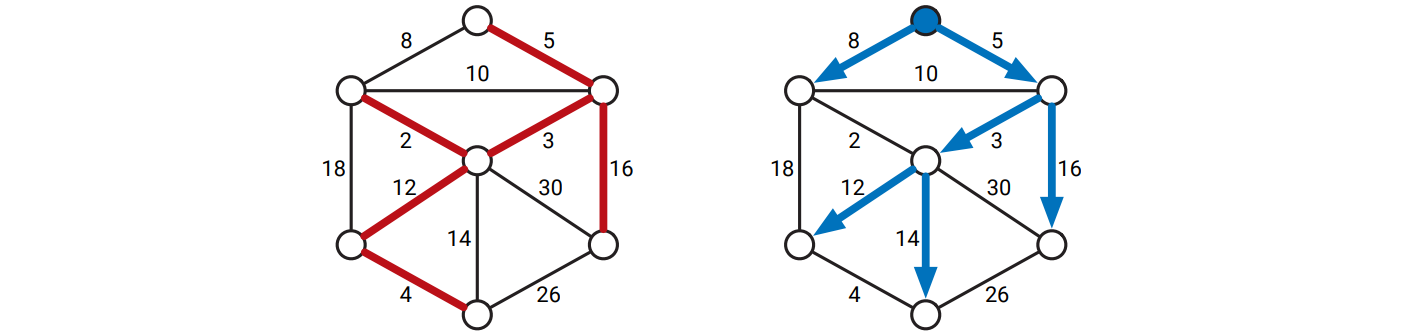
最短路木と最小全域木は両方ともある意味で最適な全域木ですが、全く異なる代物です。最短路木は根を持ち有向ですが、最小全域木は根を持たず無向です。最短路木は有向グラフに対して最も自然に定義されますが、最小全域木は無向グラフに対して最も自然に定義されます。辺の重みが全て異なるなら最小全域木は一つだけ存在しますが、最短路木はソース頂点を変えると変化します。さらに言えば、全ての頂点に対する最短路木が最小全域木と異なる辺を使うことだってあり得ます。

負辺

ほとんどの最短路問題では辺の重みが長さや距離や時間を表すので、辺の重みが非負、あるいは正であると仮定するのが自然です。しかし負辺を仮定した方が自然な最短路木アルゴリズムの応用もあります。例えば辺の重みがある頂点から別の頂点に移動するときのコストを表している場合、負の重みを持つ辺は負のコストを持った移動、つまり利益が生じる移動を表すので、それほど不自然でもありません。

負辺は多くの最短路問題において悩みの種です。なぜなら負閉路があると最短路が存在しないことがあるからです。正確に言うと、\(s\) から \(t\) への最短路が存在するのは \(s\) から \(t\) への路があって、かつ \(s\) から \(t\) へのどの路も負閉路に触れないときであり、かつそのときに限ります。負閉路に触れる \(s\) から \(t\) への任意の路について、閉路をもう一度多く回る路は必ず元の路より短くなる²ため、\(s\) から \(t\) への路で負閉路に触れるものが一つでもあるなら \(s\) から \(t\) への最短路は存在しません。

負辺を持つグラフも考えたいので、この章で明示的に考えるのは有向グラフだけです。この章で説明される全てのアルゴリズムは無向グラフにも適用できますが、上手く行くのは負の重みを持つ辺が無いときだけです。無向グラフにおける負辺の正しい取り扱いは有向グラフの場合よりもはるかに難しくなります。例えば単純に無向グラフの辺を有向辺の組にすると、負辺が二つの辺からなる負閉路を作ってしまうので上手く行きません。また負辺を含む無向最短路の部分路は最短路であるとは限らず、したがって最短路がユニークであったとしても、一つのソース頂点から他の全ての頂点に対する最短路の和集合が木とならない場合があります。

図 8.4

\(s\) からの最短路がユニークであるにもかかわらず最短路木が定義できない無向グラフ

負辺を持つ無向グラフの完全な取り扱いはこの本の範囲を超えます。Google を使ってさらに学びたい人のために言っておくと、負辺を持つ無向グラフの一つの最短路は \(O(VE + V^{2} \log V)\) 時間で計算でき、最大重みマッチングへの帰着を使います。

唯一の SSSP アルゴリズム

グラフの探索問題や最小全域木問題と同じように、多くの異なる SSSP アルゴリズムは次に示す一般的なアルゴリズムの特殊ケースとして表現できます。このアルゴリズムは Lester Ford (レスター・フォード) によって 1956 年に、そして Geroge Dantzig (ジョージ・ダンツィグ) によって 1957 年に、George Minty (ジョージ・ミンティ) によって 1958 年にそれぞれ独立に発見されました³。このアルゴリズムではグラフの各頂点 (v) が次の二つの値を保存し、これらの値によって (s) から (v) への暫定的な最短路が表されます:

\(\mathit{dist}(v)\) は暫定的な最短路 \(s \rightsquigarrow v\) があればその長さを表す。暫定的な最短路が無いなら \(\infty\) である。
\(\mathit{pred}(v)\) は暫定的な最短路 \(s \rightsquigarrow v\) があればその路における \(v\) の前者を表す。暫定的な最短路が無いなら \(\textsc{Null}\) である。

前者へのポインタ \(\mathit{pred}(s)\) によって \(s\) を根とする暫定的な木が自動的に定義されます。このポインタは一般的なグラフ走査アルゴリズムにおける親へのポインタとちょうど同じものです。アルゴリズムは各頂点の距離と前者を初期化する次の処理から始まります:

procedure \(\texttt{InitSSSP}\)(\(s\))

\(\mathit{dist}(s) \leftarrow 0\)

\(\mathit{pred}(s) \leftarrow \textsc{Null}\)

for 頂点 \(v \neq s\) do

\(\mathit{dist}(v) \leftarrow \infty\)

\(\mathit{pred}(v) \leftarrow \textsc{Null}\)

アルゴリズムの実行中に辺 \(u \rightarrow v\) が \(\mathit{dist}(u) + w(u \rightarrow v) < \mathit{dist}(v)\) を満たすとき、\(u \rightarrow v\) は緊張 (tense) していると言います。辺 \(u \rightarrow v\) が緊張しているとき \(s \rightsquigarrow u \rightarrow v\) の方が \(s \rightsquigarrow v\) よりも短いので、暫定的な最短路 \(s \rightsquigarrow v\) が正しくないことが明らかです。このとき次のように辺を緩和 (relax) することで、この明らかな過大評価を訂正 (正確には改善) できます:

procedure \(\texttt{Relax}\)(\(u \rightarrow v\))

\(\mathit{dist}(v) \leftarrow \mathit{dist}(u) + w(u \rightarrow v)\)

\(\mathit{pred}(v) \leftarrow u\)

ここまで説明すれば、Ford の一般的なアルゴリズムは一行で簡単に説明できます:

緊張した辺が無くなるまで緊張した辺を繰り返し緩和する

procedure \(\texttt{FordSSSP}\)(\(s\))

\(\texttt{InitSSSP}\)(\(s\))

while 緊張した辺が一つ以上ある do

緊張した辺を適当に選んで緩和する

\(\textsc{FordSSSP}\) が停止したときには緊張した辺が存在しないので、各頂点 \(v\) から前者 \(\mathit{pred}(v)\) へのポインタの集合が最短路木を正しく定義し、\(\mathit{dist}(v)\) が \(s\) から \(v\) への最短路の実際の長さとなります。また \(s\) から \(v\) に到達できないときには \(\mathit{dist}(v) = \infty\) であり、グラフが \(s\) から到達できる負閉路を含むときにはアルゴリズムは停止しません。

この Ford の一般的なアルゴリズムの正しさは次の簡単な命題から従います:

アルゴリズムの実行中の任意の時点で、任意の頂点 \(v\) に対する距離 \(\mathit{dist}(v)\) は \(\infty\) であるか、そうでなければ \(s\) から \(v\) へのある歩道の長さである。このことは緩和の回数に関する帰納法によって示せる。
グラフに負閉路が含まれない場合、任意の頂点 \(v\) に対して \(\mathit{dist}(v)\) は \(\infty\) であるか、そうでなければ \(s\) から \(v\) へのある単純路の長さである。またもし \(\mathit{dist}(v)\) が \(s\) から \(v\) への閉路を含む歩道の長さであった場合、その閉路は負の長さを持っている。\(G\) の単純路は有限しかないので、\(G\) に負閉路が含まれないならば緩和アルゴリズムはいずれ停止することが分かる。
\(G\) に緊張した辺が無いならば、任意の頂点 \(v\) に対して \(\mathit{dist}(v)\) は前者をたどった路 \(s \rightarrow \cdots\) \(\mathit{pred}(\mathit{pred}(v))\) \(\rightarrow \mathit{pred}(v)\) \(\rightarrow v\) の長さと等しい。なぜなら、もしある頂点 \(v\) がこの条件を満たさないなら辺 \(\mathit{pred}(v) \rightarrow v\) が緊張しているからである。
\(G\) に緊張した辺が無いならば、任意の頂点 \(v\) に対して前者をたどった路 \(s \rightarrow \cdots\) \(\mathit{pred}(\mathit{pred}(v)) \rightarrow \mathit{pred}(v) \rightarrow v\) が実は \(s\) から \(v\) への最短路である。なぜなら、もしある頂点 \(v\) がこの条件を満たさず、かつ本当の最短路における \(v\) の前者 \(u\) がこの条件を満たしているとき、辺 \(u \rightarrow v\) が緊張しているからである。この命題によってもし \(G\) が負閉路を含むならば緊張している辺が常に存在し、したがってこのアルゴリズムが停止しないことが分かる。

緊張している辺をどうやって見つけるか、あるいは緊張している辺が複数あるときにどうやって緩和する辺を選ぶかについてはこれまでに話してきませんでした。グラフ走査アルゴリズムと同じように、Ford の一般的な緩和アルゴリズムにもいくつかの異なるインスタンスが存在します。しかしグラフ走査アルゴリズムと違って、それぞれの探索戦術の正しさと効率の良さは入力グラフの構造に依存します。

この章の残りでは、Ford のアルゴリズムの最もよく知られた四つのインスタンスについて議論します。それぞれのアルゴリズムは異なるグラフのクラスに対する最適な選択肢です。一般的な正しさの証明の残りの詳細は練習問題に回して、代わりに (もっと有益な) 具体的な四つのアルゴリズムに対する正しさの証明を見ていくことにします。

重み無しグラフ: 幅優先探索

最も単純な最短路問題は全ての辺の重みが \(1\) で、路の長さが辺の数に等しい場合です。この特殊ケースではこれまでに説明したグラフ探索アルゴリズムの一つ幅優先探索 (breadth-first search, BFS) を使って答えを見つけられます。

幅優先探索は Edward Moore (エドワード・ムーア) によって発見されたとされることが多いです。実際彼は幅優先探索を ("Algorithm A" として) 1957 年に発表しており、これは初めて公表された迷路の最短路を見つけるための手続きです⁴。VLSI の配線やロボットの経路計画の文脈では、幅優先探索が Chin Yang Lee (チン・ヤン・リー) によって発見されたとされることもあります。彼が 1961 年に Moore の "Algorithm A" の応用を (きちんと Moore に言及して) いくつか発表しているためです。しかし Konrad Zuse (コンラート・ツーゼ) は 1945 年、Moore が迷路について考えを巡らせる十年以上前に、非連結グラフの成分を数えてラベルを付ける処理の幅優先探索の実装を提案しています⁶。

幅優先探索では頂点を要素とする先入れ先出しのキューを管理します。最初このキューにはソース頂点 \(s\) だけが含まれ、各反復においてアルゴリズムはキュー先端から頂点 \(u\) を \(\textsc{Pull}\) し、\(u\) から伸びる辺 \(u \rightarrow v\) を調べます。この外に向かう辺 \(u \rightarrow v\) が緊張している場合にはその辺を緩和させてから頂点 \(v\) をキューに \(\textsc{Push}\) し、キューが空になった時点でアルゴリズムは終了します:

procedure \(\texttt{BFS}\)(\(s\))

\(\texttt{InitSSSP}\)(\(s\))

\(\texttt{Push}\)(\(s\))

while キューが空でない do

\(u \leftarrow \)\(\texttt{Pull}\)()

for \(u \rightarrow v\) の形をした辺 do

if \(\mathit{dist}(v) > \mathit{dist}(u) + 1\) then

⟨⟨緊張している辺 \(u \rightarrow v\) を緩和する⟩⟩

\(\mathit{dist}(v) \leftarrow \mathit{dist}(u) + 1\)

\(\mathit{pred}(v) \leftarrow u\)

\(\texttt{Push}\)(\(v\))

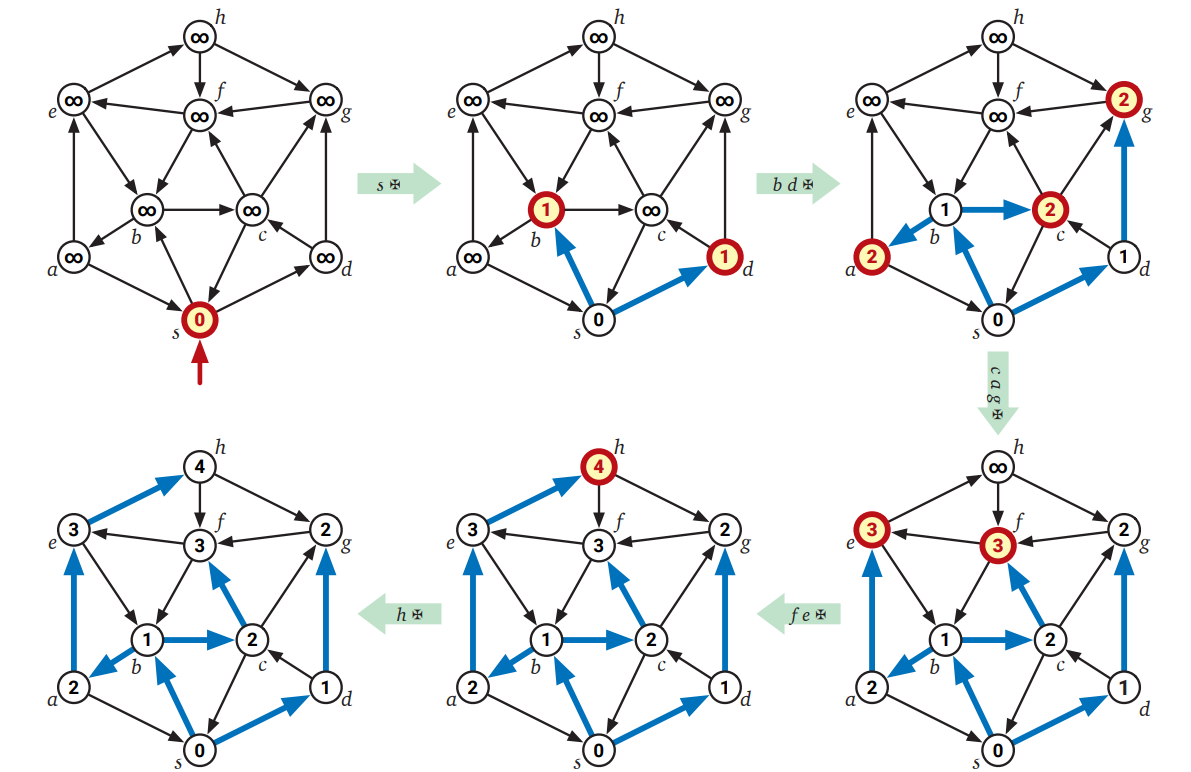
幅優先探索の解析を簡単にするために、想像上の "トークン" を考えて実行をいくつかのフェーズに分けることにします。最初に頂点を \(\textsc{Pull}\) する前にトークンをキューに \(\textsc{Push}\) しておき、その後トークンを \(\textsc{Pull}\) したときを最初のフェーズの終了とします。フェーズが終了したらすぐにトークンを \(\textsc{Push}\) して次のフェーズを始めます。こうすると最初のフェーズではソース頂点 \(s\) がスキャンされ、次のフェーズでは \(s\) に隣接する頂点がスキャンされます。アルゴリズムが終了するのはキューがトークンだけになったときです。このアルゴリズムとその実行例を以下に示します。次の点を強調しておきます: このトークンは解析を簡単にするためだけに追加されたものであり、このアルゴリズムはトークンの有無に関わらず、同じ頂点を同じ順番で \(\textsc{Push}\) および \(\textsc{Pull}\) し、出力される長さ \(\mathit{dist}\) と前者 \(\mathit{pred}\) は変化しません。

procedure \(\texttt{BFSWithToken}\)(\(s\))

\(\texttt{InitSSSP}\)(\(s\))

\(\texttt{Push}\)(\(s\))

⟨⟨最初のフェーズを始める⟩⟩

\(\texttt{Push}\)(\(\color{red}{\bigstar}\))

while キューに少なくとも一つの頂点がある do

\(u \leftarrow \)\(\texttt{Pull}\)()

if \(\color{red}{u = \bigstar}\) then

⟨⟨フェーズが終わったので、次のフェーズを始める⟩⟩

\(\texttt{Push}\)(\(\color{red}{\bigstar}\))

else

for \(u \rightarrow v\) の形をした辺 do

if \(\mathit{dist}(v) > \mathit{dist}(u) + 1\) then

⟨⟨緊張している辺 \(u \rightarrow v\) を緩和する⟩⟩

\(\mathit{dist}(v) \leftarrow \mathit{dist}(u) + 1\)

\(\mathit{pred}(v) \leftarrow u\)

\(\texttt{Push}\)(\(v\))

図 8.5

フェーズの終わりを表すトークン \(\bigstar\) を追加した幅優先探索 (赤い部分は解析のためだけにある)

次の命題を示すにあたって、次のことを強調しておきます: \(\mathit{dist}(v)\) はアルゴリズムによって管理されるただの変数です。この値が暫定的な最短路の長さを表すのは直感的には明らかですが、この時点では (まだ) \(\mathit{dist}(v)\) が \(s\) から \(v\) への最短路の長さと等しいかは分かりません。すぐに示すので心配しないでください。

命題 8.1 \(i \geq 0\) を任意の整数として、 \(i\) 番目のフェーズが終わった瞬間を考える。\(v\) を任意の頂点とすると、\(\mathit{dist}(v) = \infty\) であるか、そうでなければ \(\mathit{dist}(v) \leq i\) である。そして \(v\) がキューにあるときに限って \(\mathit{dist}(v) = i\) である。

証明 \(i\) についての帰納法で示す。\(i = 0\) の場合はすぐに分かる: 最初のフェーズが始まる直前 ("0 番目のフェーズが終わったとき") キューにはソース頂点 \(s\) とトークン \(\bigstar\) だけが含まれ、\(\textsc{InitSSSP}\) によって \(\mathit{dist}(s) \leftarrow 0\) が代入され、さらに \(v \neq s\) に対しては \(\mathit{dist}(v) \leftarrow \infty\) が代入される。よって命題が成り立つ。

\(i > 0\) を適当に選ぶ。 \(i\) 番目のフェーズが始まる直前を考えると、帰納法の仮定からキューに含まれる全ての頂点 \(u\) について \(\mathit{dist}(u) = i - 1\) であり、最後に \(\bigstar\) がある。つまりキューは次のような形をしている: \[ \rightarrow \ \ \bigstar \ \ i - 1 \ \ \cdots \ \ i - 1 \ \ \rightarrow \] したがってキューから \(\bigstar\) を \(\textsc{Pull}\) して \(i\) 番目のフェーズが終了するとき、アルゴリズムは \(\mathit{dist}(u) = i - 1\) である頂点 \(u\) を全て \(\textsc{Pull}\) している。

このフェーズで \(\textsc{Pull}\) される任意の頂点 \(u\) に対して、\(u\) から離れる辺 \(u \rightarrow v\) を考える。\(u \rightarrow v\) が緊張しているならば \(\mathit{dist}(v) \leftarrow \mathit{dist}(u) + 1\) が実行されるので \(\mathit{dist}(v) = i\) となり、その後 \(v\) はキューに \(\textsc{Push}\) される。\(i\) 番目のフェーズで距離のラベル \(\mathit{dist}(v)\) を書き換える処理はこの部分だけだから、キューには距離のラベルが \(i-1\) の頂点、トークン、\(i\) の頂点という順番で要素が並ぶ: \[ \rightarrow \ \ i \ \ \cdots \ \ i \ \ \bigstar \ \ i - 1 \ \ \cdots \ \ i - 1 \ \ \rightarrow \] よって \(i\) 番目のフェーズが終わったときにはキューにはトークンの後ろに距離のラベルが \(i\) の頂点だけが並ぶことになる: \[ \rightarrow \ \ i \ \ \cdots \ \ i \ \ \bigstar \ \ \rightarrow \]

さらに、頂点 \(v\) が最終的なキューに現れることは \(i\) 番目のフェーズで \(v\) の距離のラベルが書き換わったことと同値である。したがって \(i\) 番目のフェーズの終わったときキューには \(\mathit{dist}(v) = i\) の点が全て含まれる。また \(\mathit{dist}(v) \leq i\) も以上の議論より明らか。 \(\Box\)

命題 8.1から、\(\textsc{BFS}\) のメイン処理が距離のラベルを非減少に割り当てていくことが分かります。一方で各頂点 \(v\) に対して \(\mathit{dist}(v)\) は増加しません。また各頂点 \(v\) に対して \(\mathit{dist}(v) \leftarrow \mathit{dist}(u) + 1\) という命令は \(\mathit{dist}(v)\) 番目のフェーズで最大でも一回しか実行されないことも示せます。同様に次のことも分かります:

\(\mathit{dist}(v)\) 番目のフェーズ中、前者へのポインタ \(\mathit{pred}(v)\) は最大でも一回しか変更されない。
\(\mathit{dist}(v)\) 番目のフェーズ中、\(v\) は最大でも一回しか \(\textsc{Push}\) されない。
\(\mathit{dist}(u) + 1\) 番目のフェーズ中、\(u\) は最大でも一回しか \(\textsc{Pull}\) されない。
\(\mathit{dist}(u) + 1\) 番目のフェーズ中、任意の辺 \(u \rightarrow v\) に対して、比較 \(\mathit{dist}(v) > \mathit{dist}(u) + 1\) は最大でも一回しか実行されない。

これらの観察をまとめると、幅優先探索の実行時間が \(\pmb{O(V+E)}\) であると分かります。直感的に言えば、キューにある頂点はソース頂点 \(s\) から同じ速度で外側に向かって広がる波の波面です。この広がっていく波という比喩は 1961 年に Chin Yang Lee (チン・ヤン・リー) によって、Moore の Algorithm A を自身で実装、可視化したものを指して使われています。

また、"\(\text{if } \mathit{dist} (v) > \mathit{dist}(u) + 1\)" という条件を (明らかに) より単純な "\(\text{if } \mathit{dist}(v) = \infty\)" で置き換えることができることも分かります。他のグラフ走査アルゴリズムにおいて全ての頂点に一度だけ訪れることを保証する "印" の役割を、このアルゴリズムでは距離が果たすことになります。つまり頂点にラベル付けされた距離が有限ならばその頂点には "印が付いて" います。

図 8.6

有向グラフに対する幅優先探索の完全な実行例。キューから出てくる頂点の順番は \(s \bigstar b d \bigstar c a g \bigstar f e \bigstar h \bigstar \bigstar\) である (\(\bigstar\) がフェーズの終わりを表す)。強調された頂点がキューに入っている頂点を、青くて太い辺が成長している最小路木を表す。

しかし、最終的な距離のラベルが正しいことには証明が必要です！

定理 8.2 \(\textsc{BFS}\) が終わったとき、任意の頂点 \(v\) について、\(\mathit{dist}(v)\) は \(G\) における \(s\) から \(v\) までの最短路の長さを表す。

証明適当な頂点 \(v\) を固定し、\(G\) における任意の路 \(s = v_{0} \rightarrow\) \(v_{1} \rightarrow\) \(\cdots \rightarrow\) \(v_{l} = v\) を考える。任意の添え字 \(j\) に対して \(\mathit{dist}(v_{j}) \leq j\) であり、したがって \(\mathit{dist}(v) \leq l\) であることを示す。\(j\) に関する帰納法を使う。

\(\mathit{dist}(v_{0}) = \mathit{dist}(s) = 0\) は明らか。
任意の添え字 \(j > 0\) について、帰納法の仮定より \(\mathit{dist}(v_{j-1}) \leq j - 1\) である。キューから \(v_{j-1}\) を \(\textsc{Pull}\) したとき、\(\mathit{dist}(v_{j}) \leq \mathit{dist}(v_{j-1}) + 1\) が最初から成り立っているか、そうでなければ \(\mathit{dist}(v_{j}) \leftarrow \mathit{dist}(v_{j-1}) + 1\) という代入が実行される。いずれにせよ \(\mathit{dist}(v_{j}) \leq \mathit{dist}(v_{j-1}) + 1 \leq j\) が成り立つ。

\(\mathit{dist}(v)\) が最大でも \(s\) から \(v\) への任意の路の長さにしかならないことが示せたので、\(\mathit{dist}(v)\) は最大でも \(s\) から \(v\) への最短路の長さである。

同様の帰納法によって \(\mathit{dist}(v)\) が前者をたどった路 \(s \rightarrow\) \(\cdots \rightarrow\) \(\mathit{pred}(\mathit{pred}(v)) \rightarrow\) \(\mathit{pred}(v) \rightarrow v\) の長さと等しいことが分かるので、この路が最小路である。 \(\Box\)

有向非巡回グラフ: 深さ優先探索

有向非巡回グラフの最小路を計算するのは簡単であり、辺に重みが付いていても、その重みが負であったとしても簡単です (負閉路を気にする必要ありません。定義により、閉路が無いのですから！)。実はこれは完全に標準的な動的計画法のアルゴリズムです。

\(G\) を辺に重みの付いた有向非巡回グラフ、\(s\) を固定された開始頂点とします。任意の頂点 \(v\) に対して、\(\mathit{dist}(v)\) で \(G\) における \(s\) から \(v\) への最短路の長さを表すことにします。するとこの関数は次の単純な再帰方程式を満たします: \[ \mathit{dist}(v) = \begin{cases} 0 & \text{if } v = s \\ \min\limits_{u \rightarrow v} (\mathit{dist}(u) + w(u \rightarrow v)) & \text{それ以外} \end{cases} \] 実は、この等式は全ての有向グラフについて成り立ちます。しかしこの式が再帰方程式として定義されるのは有向非巡回グラフに対してだけです (入力グラフ \(G\) が閉路を持っているとき、この関数は無限ループに入ってしまうため)。\(G\) が DAG ならば、全ての再帰的な呼び出しはトポロジカル順序で前にある頂点を訪れるだけで必ず評価できます。こうして出来上がるアルゴリズムを次に示します:

procedure \(\texttt{DagSSSP}\)(\(s\))

for トポロジカル順序の頂点 \(v\) do

if \(v = s\) then

\(\mathit{dist}(v) \leftarrow 0\)

else

\(\mathit{dist}(v) \leftarrow \infty\)

for \(u \rightarrow v\) の形をした辺 do

if \(\mathit{dist}(v) > \mathit{dist}(u) + w(u \rightarrow v)\) then

⟨⟨緊張している辺 \(u \rightarrow v\) を緩和する⟩⟩

\(\mathit{dist}(v) \rightarrow \mathit{dist}(u) + w(u \rightarrow v)\)

図 8.7

動的計画法を使った DAG の最短路の計算

\(\mathit{dist}\) の再帰方程式の依存グラフは入力グラフ \(G\) の逆グラフです: 小問題 \(\mathit{dist}(v)\) が \(\mathit{dist}(u)\) に依存するのは \(G\) に辺 \(u \rightarrow v\) があるときだけだからです。よって \(G\) の逆に対する深さ優先探索を行って頂点を帰りがけ順に考えることで、各頂点に対する最短路の長さを \(\pmb{O(V+E)}\) 時間で計算できます。同じことですが、\(G\) のトポロジカル順序で頂点を考えるとも言えます。

この動的計画法のアルゴリズムはFord の一般的な緩和アルゴリズムのもう一つの例でもあります！ \(\mathit{dist}(v)\) の初期化をメインループの外に出し、前者へのポインタを追加する処理を加えるとこの関係がより明確になります。このアルゴリズムを次に示します:

procedure \(\texttt{DagSSSP}\)(\(s\))

\(\texttt{InitSSSP}\)(\(s\))

for トポロジカル順序の頂点 \(v\) do

for \(u \rightarrow v\) の形をした辺 do

if \(u \rightarrow v\) が緊張している then

\(\texttt{Relax}\)(\(u \rightarrow v\))

図 8.8

Ford のアルゴリズムを使って DAG の最短路を計算する (アルゴリズムとしては同一)

頂点をトポロジカル順序に考え、その頂点<strong>へ向かう</strong>辺を緩和していくことで DAG の最短路を計算する。各反復において、青くて太い辺が前者へのポインタを、赤い太字の頂点がスキャンされる頂点を表す。次の図と比較すること。 — 図 8.9

頂点をトポロジカル順序に考え、その頂点**へ向かう**辺を緩和していくことで DAG の最短路を計算する。各反復において、青くて太い辺が前者へのポインタを、赤い太字の頂点がスキャンされる頂点を表す。次の図と比較すること。

幅優先探索や Ford の緩和戦略の他のインスタンスと比べると、\(\textsc{DagSSSP}\) には少しだけ違いがあります。他の最短路アルゴリズムが頂点を調べるときは頂点から出る辺を緩和させようとするので、直感的には波面を外側に向かって押し広げるような処理をします。これに対して \(\textsc{DagSSSP}\) では頂点に向かう辺を緩和させようとするので、直感的には波面をこちら側に引っ張るような処理をします。

ただし、やってくる辺ではなく外側に向かう辺を考えるように \(\textsc{DagSSSP}\) を改変することは可能です。このすると他の最短路アルゴリズムに良く似た、 DAG の最短路を \(\pmb{O(V + E)}\) 時間で計算する別のアルゴリズムが手に入ります:

procedure \(\texttt{PushDagSSSP}\)(\(s\))

\(\texttt{InitSSSP}\)(\(s\))

for トポロジカル順序の頂点 \(\color{red}{u}\) do

for \(u \rightarrow v\) の形をした辺 do

if \(u \rightarrow v\) が緊張している then

\(\texttt{Relax}\)(\(u \rightarrow v\))

このアルゴリズムを前図と同じグラフに対して実行した様子を次の図に示します。\(\textsc{PushDagSSSP}\) の正しさは Ford の一般的な緩和戦略の正しさから従いますが、頂点のトポロジカル順序に関する帰納法を使って直接示すのも難しくありません。

頂点をトポロジカル順序に考え、その頂点<strong>から出る</strong>辺を緩和していくことで DAG の最短路を計算する。各反復において、青くて太い辺が前者へのポインタを、赤い太字の頂点がスキャンされる頂点を表す。前の図と比較すること。 — 図 8.10

頂点をトポロジカル順序に考え、その頂点**から出る**辺を緩和していくことで DAG の最短路を計算する。各反復において、青くて太い辺が前者へのポインタを、赤い太字の頂点がスキャンされる頂点を表す。前の図と比較すること。

最良優先: Dijkstra のアルゴリズム

幅優先探索では FIFO を使っていましたが、この FIFO を頂点 \(v\) に対する鍵が暫定的な距離 \(\mathit{dist}(v)\) であるような優先度付きキューで置き換えると、別の最短路アルゴリズムが手に入ります。1957 年にこのアルゴリズムを初めて "出版" したのは Michael Leyzorek (マイケル・レイゾレク) を中心とするケース工科大学の研究者チームで、米陸軍電子機器性能証明実験場の戦闘開発部署に対する定期報告書でのことでした。同じアルゴリズムは Edsger Dijkstra (エドガー・ダイクストラ) によって 1956 年に独立に発見され (1959 年に出版され)、1960 年には George Minty (ジョージ・ミンティ) によって、同じく 1960 年には P.D. Whiting (P・D・ホワイティング) と J.A. Hillier (J・A・ヒラー) によっても独立に発見されています。また 1958 年には George Dantzig (ジョージ・ダンツィグ) がほとんど同じアルゴリズムを示しています。古い文献ではこのアルゴリズムが "Minty のアルゴリズム" と呼ばれることもありますが、現在では世界中で "Dijkstra のアルゴリズム" と呼ばれており、スティグラーの法則に完全に従っています⁷。Dijkstra のアルゴリズムの疑似コードを次に示します:

procedure \(\texttt{Dijkstra}\)(\(s\))

\(\texttt{InitSSSP}\)(\(s\))

\(\texttt{Insert}\)(\(s, 0\))

while 優先度付きキューが空でない do

\(u \leftarrow \)\(\texttt{ExtractMin}\)()

for \(u \rightarrow v\) の形をした辺 do

if \(u \rightarrow v\) が緊張している then

\(\texttt{Relax}\)(\(u \rightarrow v\))

if \(v\) が優先度付きキューにある then

\(\texttt{DecreaseKey}\)(\(v, \mathit{dist}(v)\))

else

\(\texttt{Insert}\)(\(v, \mathit{dist}(v)\))

簡単な帰納法によって、アルゴリズムの実行中に \(u \rightarrow v\) が緊張しているのは頂点 \(u\) が優先度付きキューにあるときか、そうでなければ \(u\) を優先度付きキューから \(\textsc{ExtractMin}\) したときであることが示せます。よって Dijkstra のアルゴリズムが Ford の一般的な戦略のインスタンスであり、したがって \(G\) に負閉路が含まれない場合には最短路を正しく計算することが分かります。

負辺無し

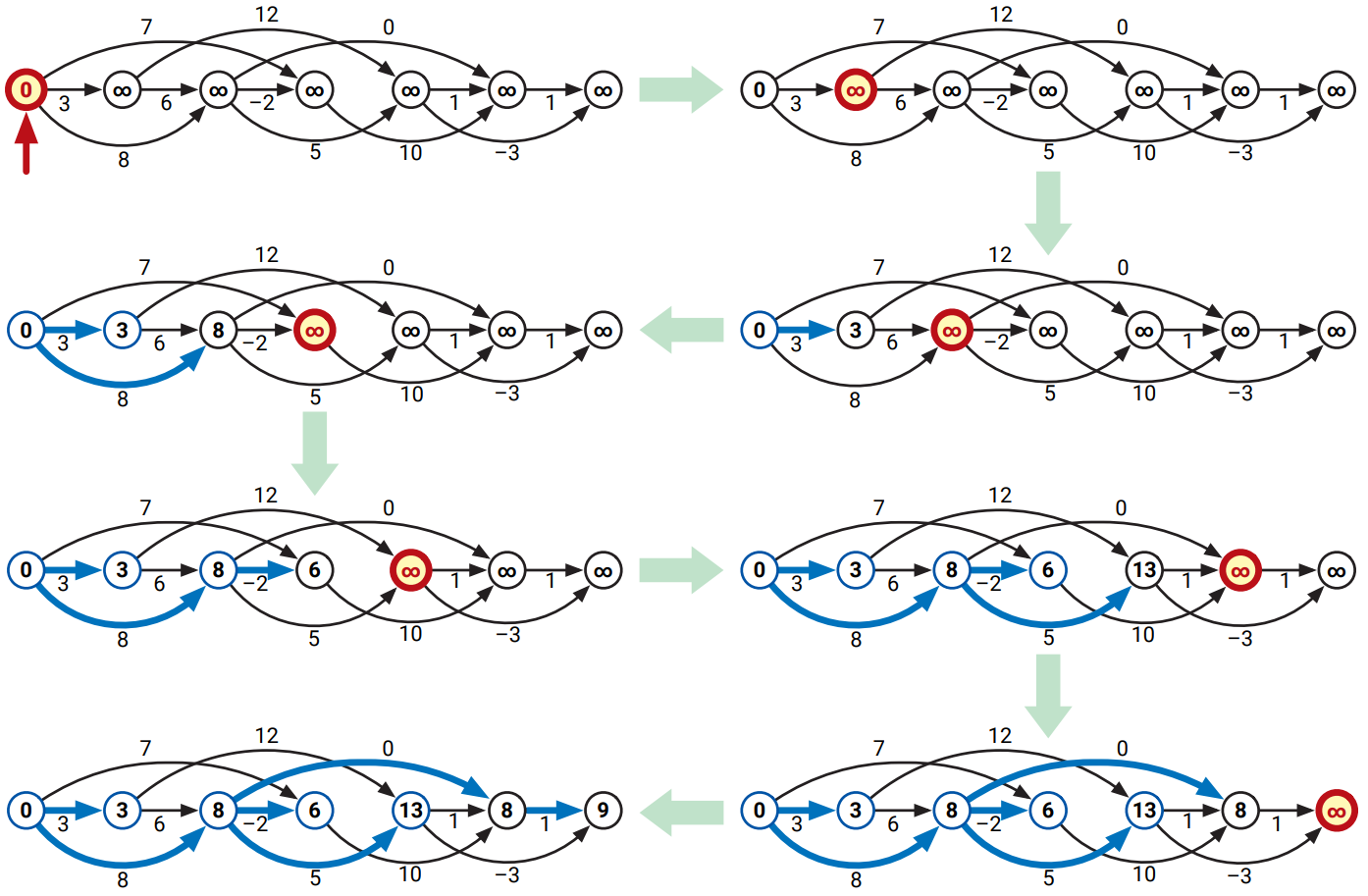
Dijkstra のアルゴリズムはグラフに負辺が含まれないときにとても解析しやすい動作をします。この設定ではアルゴリズムによって作られる波面がソース頂点 \(s\) からの距離が大きくなる順番で広がっていくので、動作は幅優先探索と似ています。実行の様子を次の図に示します:

図 8.12

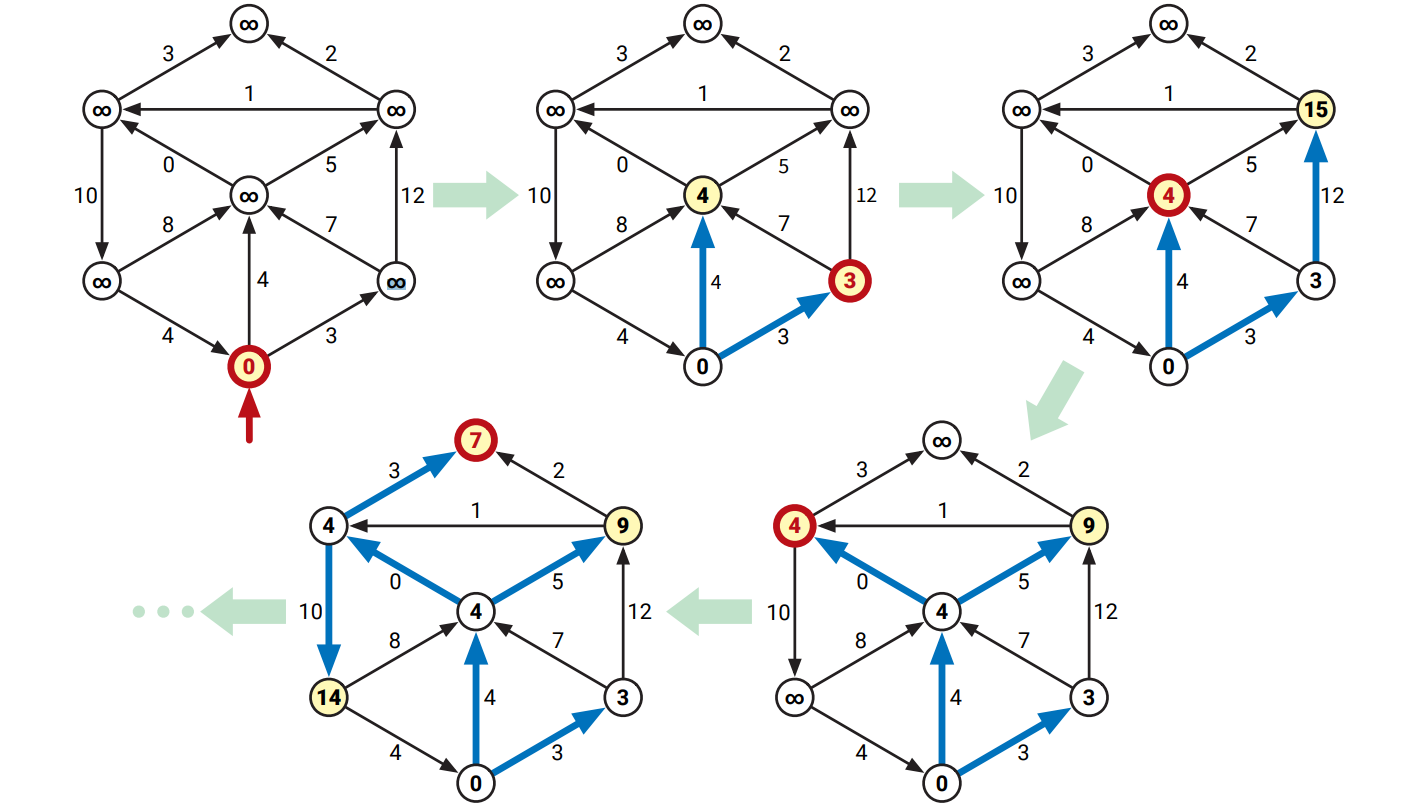
負辺を持たないグラフに対して Dijkstra のアルゴリズムを実行したときの最初の四反復。各反復において、青くて太い辺が前者からの辺を、黄色い頂点が優先度付きキューにある頂点を、太字の赤い頂点が次にスキャンされることを表す。

波面の比喩をたどっていけば、この設定の下での Dijkstra のアルゴリズムの正しさの直接的な証明ができます。任意の整数 \(i\) に対して、\(i\) 番目の \(\textsc{ExtractMin}\) が返す頂点を \(u_{i}\) と表し、この \(\textsc{ExtractMin}\) の直後の \(\mathit{dist}(u_{i})\) の値を \(d_{i}\) で表すことにします。例えば \(u_{1} = s\) および \(d_{1} = 0\) です。同じ頂点が複数回 \(\textsc{ExtractMin}\) される可能性があるので、まだこの時点では \(u_{i}\) が全て異なるとは仮定できません。

命題 8.3 \(G\) に負辺が無いならば、任意の整数 \(i < j\) について \(d_{i} \leq d_{j}\) が成り立つ。

証明 \(G\) に負辺が含まれないとし、\(i\) を適当な添え字とする。\(d_{i+1} \geq d_{i}\) を示せば十分であり、考える場合は二つある。

メインループの \(i\) 番目のループで辺 \(u_{i} \rightarrow u_{i+1}\) が緩和される場合。このとき \(i\) 番目の反復の終了時には \(\mathit{dist}(u_{i+1}) = \mathit{dist}(u_{i}) + w(u_{i} \rightarrow w_{i+1})\) であり、負辺が存在しないことから \(\mathit{dist}(u_{i+1}) \geq \mathit{dist}(u_{i})\) が成り立つ。
メインループの \(i\) 番目のループで辺 \(u_{i} \rightarrow u_{i+1}\) が緩和されないか、辺 \(u_{i} \rightarrow u_{i+1}\) が存在しない場合。このとき \(i\) 番目の反復の開始時点で \(u_{i+1}\) が優先度付きキューにあり、反復の最初の \(\textsc{ExtractMin}\) で \(u_{i}\) が帰っていることから \(\mathit{dist}(u_{i+1}) \geq \mathit{dist}(u_{i})\) である。さらに \(i\) 番目の反復で \(\mathit{dist}(u_{i+1})\) の値は変化しないので、 \(\mathit{dist}(u_{i+1}) \geq \mathit{dist}(u_{i})\) が成り立つ。

どちらの場合においても \(d_{i+1} \geq d_{i}\) であり、簡単な帰納法から示したい命題が示せる。 \(\Box\)

命題 8.4 \(G\) に負辺が無いならば、\(G\) の任意の頂点は最大でも一度だけ優先度付きキューから \(\textsc{ExtractMin}\) される。

証明背理法で示す。\(v\) が二度以上 \(\textsc{ExtractMin}\) されるとする。具体的には、\(v\) が \(i\) 番目の反復で \(\textsc{ExtractMin}\) され、\(j\) 番目の反復で \(\textsc{Insert}\) され、\(k\) 番目の反復でもう一度 \(\textsc{ExtractMin}\) されるとする (\(i < j < k\))。一つ前の命題の記法を使うと、\(v = u_{i} = u_{k}\) である。

距離のラベル \(\mathit{dist}(v)\) は増加せず、\(\mathit{dist}(v)\) は \(j\) 番目の反復で \(\textsc{Insert}\) される前に狭義に減少するので、\(d_{i} > d_{k}\) である。よって一つ前の命題より、\(G\) には少なくとも一つの負辺が含まれることになるが、これは問題の仮定と矛盾する。 \(\Box\)

命題 8.4 から全ての頂点が最大でも一度だけスキャンされ、全ての辺が最大でも一回だけ緩和されることが分かります。しかし幅優先探索と違って、距離のラベル \(\mathit{dist}(v)\) は複数回書き換えられます。最初に \(\mathit{dist}(v)\) が書き換えられるのは \(\mathit{dist}(v) = \infty\) から値が変わるときで、その直後 \(v\) は優先度付きキューに \(\textsc{Insert}\) され、その後は \(\textsc{DecreaseKey}\) によって \(\mathit{dist}(v)\) が変更されます。一度 \(v\) が \(\textsc{ExtractMin}\) されれば、それ以降 \(v\) の距離のラベルは変化しません。

正しさの証明の残りの部分は幅優先探索のものとほとんど同じです。

定理 8.5 \(G\) に負辺が無いならば、\(\textsc{Dijkstra}(s)\) が停止したとき、任意の頂点 \(v\) に対して \(\mathit{dist}(v)\) は \(s\) から \(v\) への最短路の長さと等しい。

証明 \(v\) を任意の頂点とし、任意の路 \(s = v_{0} \rightarrow\) \(v_{1} \rightarrow\) \(\cdots \rightarrow\) \(v_{l} = v\) を考える。任意の添え字 \(j\) に対して、部分路 \(v_{0} \rightarrow\) \(v_{1} \rightarrow\) \(\cdots \rightarrow v_{j}\) の長さを \(L_{j}\) とする。任意の \(j\) について\(\mathit{dist}(v_{j}) \leq L_{j}\) を帰納法で示す。

\(\mathit{dist}(v_{0}) = \mathit{dist}(s) = 0 = L_{0}\) は明らか。
\(j > 0\) を任意の整数とする。帰納法の仮定から \(\mathit{dist}(v_{j-1}) \leq L_{j-1}\) であり、優先度付きキューから \(v_{j-1}\) を \(\textsc{Pull}\) したとき \(\mathit{dist}(v_{i}) \leq \mathit{dist}(v_{j-1}) + w(v_{j-1} \rightarrow v_{j})\) が最初から成り立っているか、そうでなければ \(\mathit{dist}(v_{i}) \leftarrow \mathit{dist}(v_{j-1}) + w(v_{j-1} \rightarrow v_{j})\) という代入が行われる。よって \[ \mathit{dist}(v_{j}) \leq \mathit{dist}(v_{j-1}) + w(v_{j-1} \rightarrow v_{j}) \leq L_{j-1} + w(v_{j-1} \rightarrow v_{j}) = L_{j} \] が成り立つ。

\(\mathit{dist}(v)\) が最大でも \(s\) から \(v\) への任意の路の長さにしかならないことが示せたので、\(\mathit{dist}(v)\) は \(s\) から \(v\) への最短路の長さである。

最後に Dijkstra のアルゴリズムの実行時間を調べます。\(\textsc{Dijkstra}\) は最大で \(E\) 回の \(\textsc{DecreaseKey}\) と \(V\) 回の \(\textsc{Insert}\) と \(V\) 回の \(\textsc{ExtractMin}\) を行います。標準的な二分ヒープを使うとこれらの操作は全て \(O(\log V)\) 時間で行えるので、アルゴリズム全体の実行時間は \(\pmb{O(E\log V)}\) です⁸。

グラフに負辺が無いことが事前にわかっているなら、Dijkstra のアルゴリズムを単純にできます。具体的には、初期化処理において優先度付きキューに全ての頂点を入れておき、メインループでは \(\textsc{DecreaseKey}\) だけを呼びます。ほとんどのアルゴリズムの教科書で紹介されているのはこのバージョンの Dijkstra のアルゴリズムであり、Wikipedia および Dijkstra の原著論文に載っているのもこのバージョンです。また五章で説明した "最良優先探索" もこの形をしていました。

procedure \(\texttt{NonNegativeDijkstra}\)(\(s\))

\(\texttt{InitSSSP}\)(\(s\))

for 頂点 \(v\) do

\(\texttt{Insert}\)(\(\color{red}{v, \mathit{dist}(v)}\))

while 優先度付きキューが空でない do

\(u \leftarrow \)\(\texttt{ExtractMin}\)()

for \(u \rightarrow v\) の形をした辺 do

if \(u \rightarrow v\) が緊張している then

\(\texttt{Relax}\)(\(u \rightarrow v\))

\(\texttt{DecreaseKey}\)(\(\color{red}{v, \mathit{dist}(v)}\))

図 8.13

負辺が無いグラフだけを扱える単純化された Dijkstra のアルゴリズム (\(\textsc{Dijkstra}\) からの変化が赤で示されている)

❤ 負辺あり

グラフに負辺が含まれる場合、\(\textsc{NonNegativeDijkstra}\) は最短路を正しく計算できません。また辺の重みが全て正だったとしても、 \(\textsc{NonNegativeDijkstra}\) は (理論上も、実際のプログラムでも) \(\textsc{Dijkstra}\) より高速なわけではありません。このことから、\(\textsc{NonNegativeDijkstra}\) ではなくて \(\textsc{Dijkstra}\) こそが "Dijkstra のアルゴリズム" と呼ぶにふさわしいアルゴリズムであると私は考えています。Edsger Dijkstra がかつて言ったように、「たまに遅くなる正しいアルゴリズムは、たまに間違う速いアルゴリズムよりも優れている」からです！それに、遅くなると言っても実際はほとんど遅くなりません。

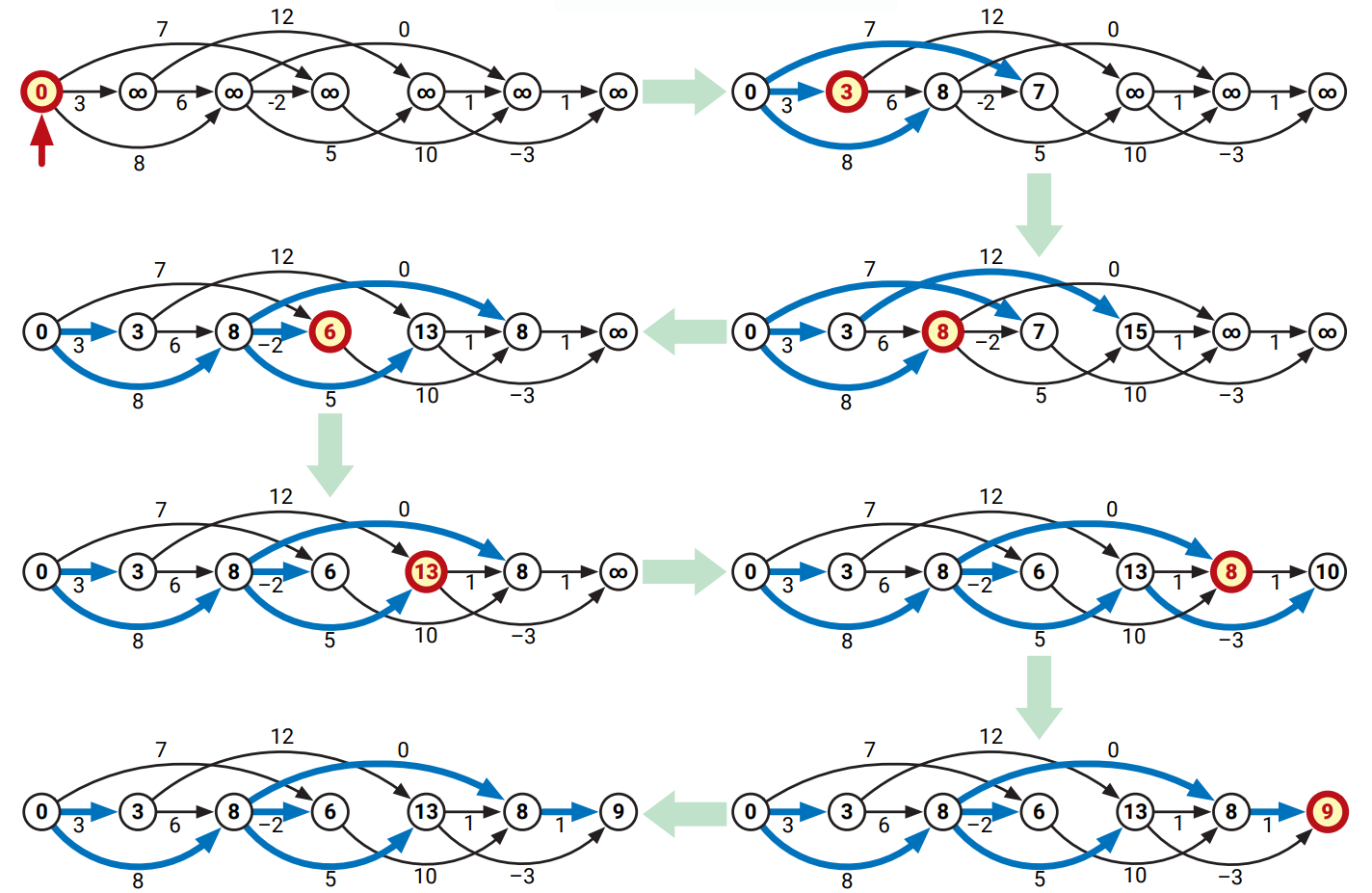
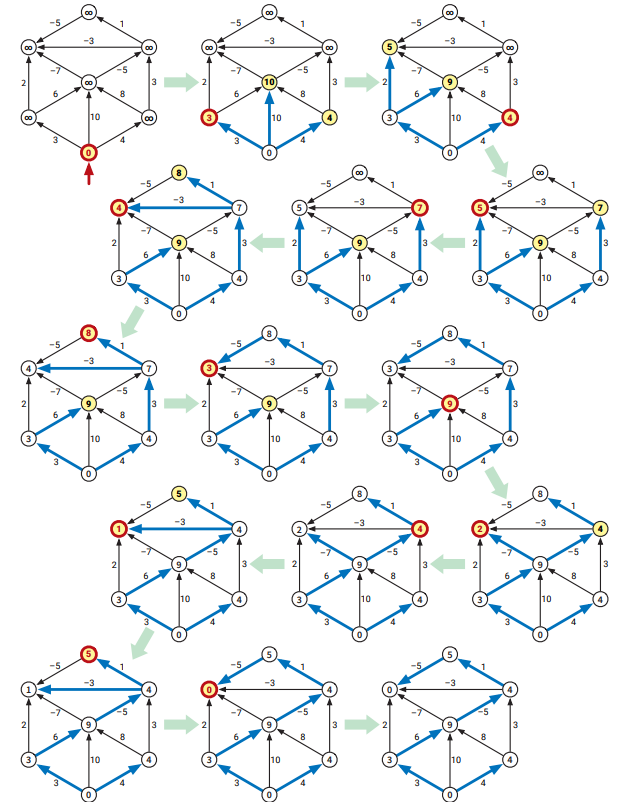
グラフが負辺を持つ場合には、これまで使ってきた "波面を広げる" という比喩は残念なことに使えなくなります。同じ頂点が複数回 \(\textsc{ExtractMin}\) されることがあり、同じ辺が複数回緩和されることもあり、また各頂点の距離のラベルが常に大きくなるとは限りません。次の図に示す例では左上の頂点が六回 \(\textsc{ExtractMin}\) されており、上の辺は全て二回ずつ緩和されています。

図 8.15

負辺を持ったグラフに対する Dijkstra のアルゴリズムの完全な実行例。各反復において、青くて太い辺が前者へのポインタを、黄色い頂点が優先度付きキューにある頂点を、赤い太字の頂点が次にスキャンする頂点を表す。図 8.16 と比較すること。

実は、負閉路が含まれないこと以外の制約が無いグラフに対する \(\textsc{Dijkstra}\) の最悪計算時間は指数的になります。次に示すグラフは \(\textsc{Dijkstra}\) が \(\Theta(2^{V/2})\) 回の緩和を行う (Douglas Shier と Christoph Witzgall によって発見された) グラフのクラスです⁹。\(\Theta(2^{V})\) 回の緩和が行われるさらに複雑なグラフの族もあります (練習問題とします)。しかし現実のグラフに対しては、負辺があったとしても Dijkstra のアルゴリズムはたいてい高速に実行できます。

図 8.14

\(\textsc{Dijkstra}\) の実行時間が指数時間となる、負辺を持った有向グラフ

スベテの辺を緩和する: Bellman-Ford

Ford の一般的な最短路アルゴリズムの一番単純な実装のアイデアは、1954 年に Alfonso Shimbel (アルフォンソ・シンベル) によって提案され、1957 年に Edward Moore (エドワード・ムーア) によってより詳細に示されました。同じアルゴリズムは 1957 年には Max Woodbury (マックス・ウッドベリー) と George Dantzig (ジョージ・ダンツィグ) によって、1958 年には Richard Bellman (リチャード・ベルマン) によって、同じく 1958 年に Geroge Minty (ジョージ・ミンティ) によってそれぞれ独立に発見されています (Woodbury も Dantzig も Minty もアルゴリズムを発表することはありませんでした)。スティグラーの法則に完璧に従って、このアルゴリズムは Bellman-Ford のアルゴリズム¹⁰ として世界中に知られています。こう呼ばれているのは、1956 年に Ford によって発表された辺の緩和を使った定式化について Bellman がはっきりと言及していたためです。ただし "Bellman-Kalaba" という名前¹¹を使う著者もいますし、古い文献には "Bellman-Shimbel" という名前も出てきます。

Shimbel / Moore / Woodbury-Dantzig / Bellman-Ford / Kalaba / Minty / Brosh¹² のアルゴリズムは次の一行に要約できます:

Bellman-Ford: 緊張している辺をスベテ緩和し、再帰する。

procedure \(\texttt{BellmanFord}\)(\(s\))

\(\texttt{InitSSSP}\)(\(s\))

while 緊張している辺が一つでもある do

for \(u \rightarrow v\) の形をした辺 do

if \(u \rightarrow v\) が緊張している then

\(\texttt{Relax}\)(\(u \rightarrow v\))

任意の頂点 \(v\) と非負整数 \(i\) に対して、 \(G\) における辺を \(i\) 個以下しか使わない \(s\) から \(v\) への最短の歩道の長さを \(\pmb{\mathit{dist}_{\leq i}(v)}\) と表すことにします。例えば \(\mathit{dist}_{\leq 0}(s) = 0\) および全ての \(v \neq s\) について \(\mathit{dist}_{\leq 0}(v) = \infty \) です。Bellman-Ford の正しさと効率の証明において鍵となるのは次の命題です。

命題 8.6 \(v\) を任意の頂点、\(i\) を非負整数とする。\(\textsc{BellmanFord}\) のメインループの \(i\) 回目の反復が終了した時点において、\(\mathit{dist}(v) \leq \mathit{dist}_{\leq i} (v)\) が成り立つ。

証明 \(i\) についての帰納法で示す。\(i = 0\) の場合は自明だから、\(i > 0\) とする。\(v\) を適当な頂点とし、頂点を \(i\) 個以下しか含まない \(s\) から \(v\) への最短歩道を \(W\) とする (最短の歩道がいくつかある場合は適当に選ぶ)。定義により \(W\) の長さは \(\mathit{dist}_{\leq i} (v)\) に等しい。考えるべきケースは二つある。

\(W\) に辺が含まれないとき、\(W\) は \(s\) から \(s\) への自明な歩道だから、\(v = s\) かつ \(\mathit{dist}_{\leq i}(s) = 0\) である。\(\textsc{InitSSSP}\) において \(\mathit{dist}(s) \leftarrow 0\) と代入し、\(\mathit{dist}(s)\) はそれ以降増加しないので \(\mathit{dist}(s) \leq 0 = \mathit{dist}_{\leq i}(s)\) が成り立つ。
そうでないとき、\(W\) の最後の辺を \(u \rightarrow v\) とする。帰納法の仮定により、\(i - 1\) 回の反復の後 \(\mathit{dist}(u) \leq \mathit{dist}_{\leq i-1}(u)\) が成り立っている。\(i\) 回目の反復では \(\mathit{dist}(v) \leq \mathit{dist}(u) + w(u \rightarrow v)\) が最初から成り立っているか、そうでなければ \(\mathit{dist}(v) \leftarrow \mathit{dist}(u) + w(u \rightarrow v)\) という代入が行われる。いずれの場合でも、\(\mathit{dist}(v) \leq \mathit{dist}(u) + w(u \rightarrow v)\) が成り立つ。加えて \(\mathit{dist}(v)\) はこの反復で増加しないので、\(\mathit{dist}(v) \leq\) \(\mathit{dist}(u) + w(u \rightarrow v) =\) \(\mathit{dist}_{\leq i} (v)\) が成り立つ。

いずれの場合でも、\(i\) 回目の反復が終わったとき \(\mathit{dist}(v) \leq \mathit{dist}_{\leq i}(v)\) が成り立つ。 \(\Box\)

入力グラフに負閉路が存在しないなら、\(s\) から任意の頂点への最短路は最大でも \(V-1\) 個の辺を持つ単純路です。よって \(\textsc{BellmanFord}\) は最大でも \(V-1\) 回の反復で正しい最小路を計算して停止します。言い方を変えれば、もし \(V-1\) 回の反復を行ってもなお緊張している辺が残っているなら、入力グラフは負閉路を持ちます！このことを使えば、アルゴリズムを次のように書き換えて、負閉路を見つけたときにエラーを出すようにできます。

このアルゴリズムの内側の反復は明らかに \(O(E)\) だけ時間がかかるので、全体の実行時間は \(\pmb{O(VE)}\) です。またこの Bellman-Ford のアルゴリズムの実装は負辺がある場合でも、さらには負閉路がある場合でも効率良く計算を行えます。

procedure \(\texttt{BellmanFord}\)(\(s\))

\(\texttt{InitSSSP}\)(\(s\))

for \(V - 1\) 回繰り返す do

for \(u \rightarrow v\) の形をした辺 do

if \(u \rightarrow v\) が緊張している then

\(\texttt{Relax}\)(\(u \rightarrow v\))

for 辺 \(u \rightarrow v\) do

if \(u \rightarrow v\) が緊張している then

return "入力グラフに負閉路がある！"

しかし辺の重みが非負である場合には、少なくとも最悪計算時間は Dijkstra のアルゴリズムの方が速くなります (ただ実際にプログラムを動かすと、負辺が含まれるグラフであっても Dijkstra のアルゴリズムの方が Bellman-Ford のアルゴリズムよりも速くなることが多いです)。

Moore による改善

Moore も Bellman も、ここに説明した Bellman-Ford アルゴリズムを示したわけではありませんでした。Moore は重み無しグラフに対する幅優先探索 ("Algorithm A") を発表したのと同じ論文で、彼のバージョンの Bellman-Ford アルゴリズム ("Algorithm D") を示しています。Moore のアルゴリズムの最悪計算量は \(O(VE)\) で \(\textsc{BellmanFord}\) と変わりませんが、Moore のアルゴリズムは "明らかに" 緊張していない辺を飛ばすので、現実のデータに対しては \(\textsc{BellmanFord}\) よりも各段に速いことが多いです。このアルゴリズムを次に示します:

procedure \(\texttt{Moore}\)(\(s\))

\(\texttt{InitSSSP}\)(\(s\))

\(\texttt{Push}\)(\(s\))

⟨⟨最初のフェーズを始める⟩⟩

\(\texttt{Push}\)(\(\color{red}{\bigstar}\))

while キューに少なくとも一つの頂点がある do

\(u \leftarrow \)\(\texttt{Pull}\)()

if \(\color{red}{u = \bigstar}\) then

⟨⟨フェーズが終わったので、次のフェーズを始める⟩⟩

\(\texttt{Push}\)(\(\color{red}{\bigstar}\))

else

for \(u \rightarrow v\) の形をした辺 do

if \(u \rightarrow v\) が緊張している then

\(\texttt{Relax}\)(\(u \rightarrow v\))

if \(v\) がキューに無い then

\(\texttt{Push}\)(\(v\))

図 8.16

Moore の最短路アルゴリズム (トークンを使う赤い部分は解析のためだけにある)

Moore は幅優先探索に二つの変更を加えることで最短路アルゴリズムを作っています。まず辺の重みを考えるために内側のループの \(+ \ 1\) を \(+ \ w(u \rightarrow v)\) で置き換え、次にキューに同じ頂点が複数入ることが無いように \(\textsc{Insert}\) の前にキューの中を調べます¹³。

前に幅優先探索 (BFS) に対して行ったのと同じように、解析を簡単にするためのトークンを導入してアルゴリズムの実行を複数のフェーズに分けます。BFS と同じように、トークンがキューに \(\textsc{Push}\) されるときにフェーズが始まり、トークンがキューから \(\textsc{Pull}\) されたときにフェーズが終わります。そしてキューがトークンだけになったらアルゴリズムの終わりです。

図 8.17

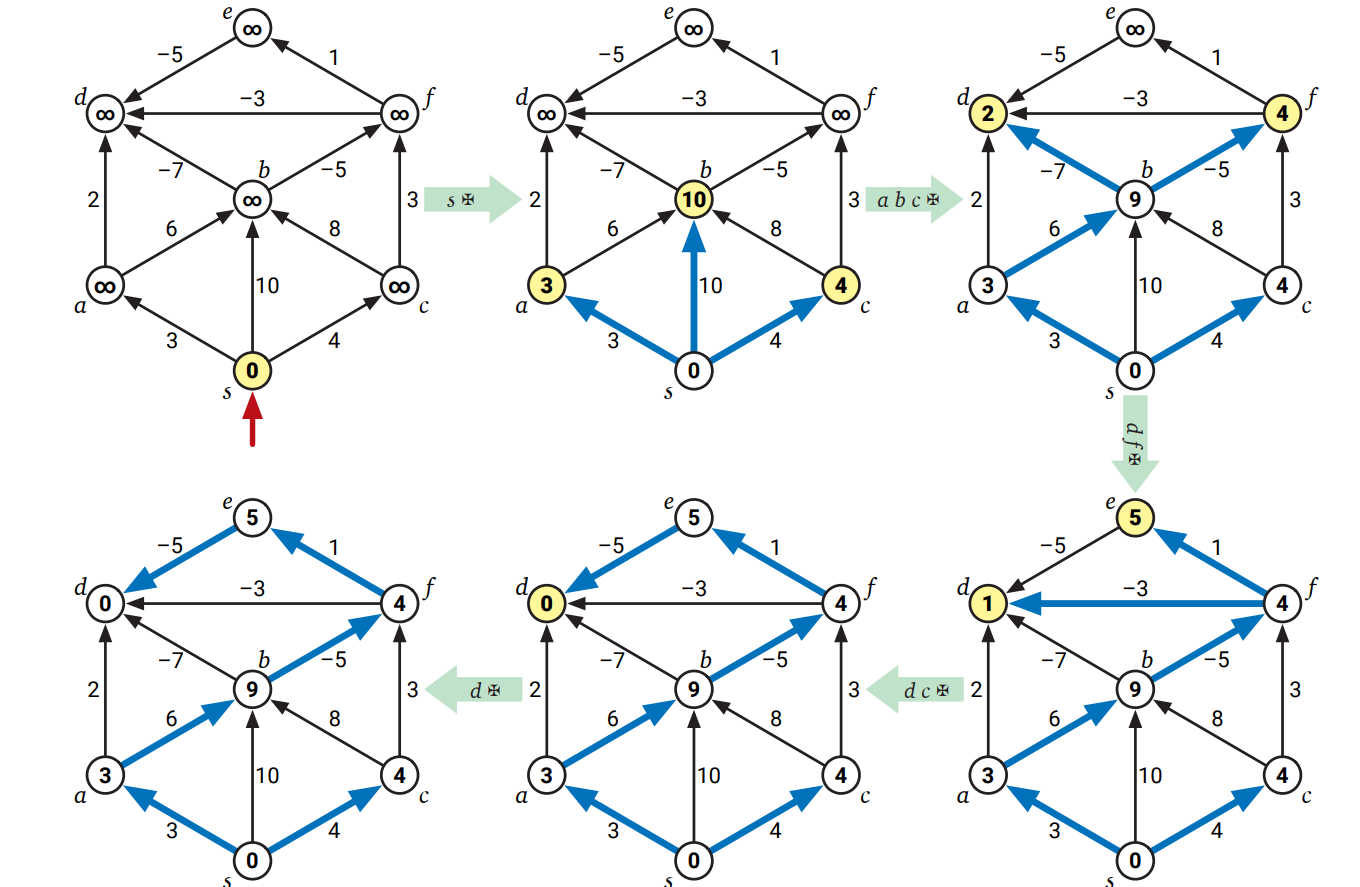
負辺を持つグラフに対する Moore のアルゴリズムの完全な実行例。キューから \(\textsc{Pull}\) される頂点の順番は \(s \bigstar a b c \bigstar d f \bigstar d e \bigstar d e \bigstar \bigstar\) である (\(\bigstar\) がフェーズの終わりのトークンを表す)。各反復において、青くて太い辺が前者へのポインタを、黄色い頂点が優先度付きキューにある頂点を、赤い太字の頂点が次にスキャンする頂点を表す。図 8.6 および図 8.15 と比較すること。

任意の時点でキューには同じ頂点のコピーが多くとも一つしか含まれず、キューにある全ての頂点はフェーズごとに最大一度だけ \(\textsc{Pull}\) されるので、各フェーズで辺 \(u \rightarrow v\) は多くとも一回しか緊張しているかどうかのチェックを受けません。さらにフェーズが始まった時点で緊張している辺は全てそのフェーズで緩和されます (フェーズ中に緊張した辺が同じフェーズ中に緩和されることはあり得ます。またフェーズ中に緩和された辺がそのフェーズ中に緊張することもあり得ます)。

\(\textsc{BellmanFord}\) は全ての辺を総当たりで調べていたので、以上の説明により、\(\textsc{Moore}\) はキューを使って辺を管理するように改善した \(\textsc{BellmanFord}\) と言うことができます。以前と同様の帰納法による証明を使うと、命題 8.6 と同様の命題を示せます:

命題 8.7 任意の頂点 \(v\) と非負整数 \(i\) について、\(\textsc{Moore}\) の \(i\) 番目のフェーズが終わったとき \(\mathit{dist}(v) \leq \mathit{dist}_{\leq i} (v)\) が成り立つ。

よってグラフに負閉路が無いならば、\(\textsc{Moore}\) は最大 \(V-1\) 回のフェーズの後に停止します。各フェーズにおいて各頂点は最大でも一回スキャンされ、各辺は最大でも一回緩和されるので、一度のフェーズの最悪計算時間は \(O(E)\) であり、\(\textsc{Moore}\) アルゴリズム全体の実行時間は \(\pmb{O(VE)}\) です。しかし実際に実装すると、\(\textsc{Moore}\) は \(\textsc{BellmanFord}\) よりもはるかに速く最短路を計算します。\(\textsc{Moore}\) はそれまでのフェーズで \(\mathit{dist}(u)\) が変化した辺 \(u \rightarrow v\) だけをスキャンするからです。

入力グラフに負閉路がある場合、\(\textsc{Moore}\) は停止しません。ですが幸運にも、\(\textsc{BellmanFord}\) と同じように \(\textsc{Moore}\) を負閉路がある場合にはそれを報告するように簡単に変更できます。おそらく一番簡単な方法は、実際にトークンを管理して、トークンをキューから \(\textsc{Pull}\) した回数を数えるというものでしょう。こうすると、入力グラフに負閉路があることは、\(n-1\) 個目のトークンをキューから \(\textsc{Pull}\) した直後にキューが空でないことと同値になります。

動的計画法による定式化

彼の名前の付いたほとんど全てのものと同じように、Richard Bellman は "Bellman-Ford" の最短路アルゴリズムの導出に動的計画法を使いました。以前と同様に最短路の長さの再帰的な定義を最初に考えましょう。もしかすると、有向非巡回グラフに対して使ったのと同じ、次の等式を使いたくなるかもしれません: \[ \mathit{dist}(v) = \begin{cases} 0 & \text{if } v = s \\ \min\limits_{u \rightarrow v} (\mathit{dist}(u) + w(u \rightarrow v)) & \text{それ以外} \end{cases} \] 残念ながら、グラフが DAG でない場合、この再帰方程式は正しくありません！ グラフに閉路 \(u \rightarrow v \rightarrow w \rightarrow u\) が含まれるとすると、\(\mathit{dist}(w)\) を計算するにはまず \(\mathit{dist}(v)\) を計算しなくてはならず、\(\mathit{dist}(v)\) のためには \(\mathit{dist}(u)\) の値が必要ですが、\(\mathit{dist}(u)\) のためには \(\mathit{dist}(w)\) が必要となります。つまり、グラフに閉路が含まれると無限ループになってしまいます！

正しい再帰方程式を得るには、グラフの構造に関するパラメータを関数に渡す必要があります。このパラメータは再帰的な呼び出しのたびにひとつずつ減っていき、0 になったときの関数の値は自明となるようなパラメータです。Bellman は路が含むことができる辺の最大数を追加のパラメータとして選びました¹⁴。

前述の解析と同じように、\(\mathit{dist}_{\leq i}(v)\) で \(s\) から \(v\) への辺が \(i\) 個以下の歩道の中で最短のものの長さを表すことにします。Bellman が気付いたのは、この関数が満たす次の ~~Bellman の等式~~ 再帰方程式です: \[ \mathit{dist}_{\leq i}(v) = \begin{cases} 0 & \text{if } i = 0 \text{ and } v = s \\ \infty & \text{if } i = 0 \text{ and } v \neq s \\ \min \left\lbrace \begin{array}{c} \mathit{dist}_{\leq i - 1}(v) \\ \min\limits_{u \rightarrow v} (\mathit{dist}_{\leq i - 1} (u) + w(u \rightarrow v)) \end{array} \right\rbrace & \text{ それ以外} \end{cases} \]

グラフに負閉路が無いとすると、最短路問題の目標は全ての頂点 \(v\) に対する \(\mathit{dist}_{\leq V - 1}(v)\) の計算です。この再帰方程式を動的計画法を使って計算するアルゴリズムを次に示します。ここで \(\mathit{dist}[i, v]\) が \(\mathit{dist}_{\leq i} (v)\) の値を保持します。最終的に計算される最短路の長さの正しさは再帰方程式の正しさから従います。また実行時間が \(O(VE)\) であるのは明らかです。

procedure \(\texttt{BellmanFordDP}\)(\(s\))

\(\mathit{dist}[0, s] \leftarrow 0\)

for 頂点 \(v \neq s\) do

\(\mathit{dist}[0,v] \leftarrow \infty\)

for \(i \leftarrow 1\) to \(V - 1\) do

for 頂点 \(v\) do

\(\mathit{dist}[i, v] \leftarrow \mathit{dist}[i - 1, v]\)

for \(u \rightarrow v\) の形をした辺 do

if \(\mathit{dist}[i, v] > \mathit{dist}[i-1, u] + w(u \rightarrow v)\) then

\(\mathit{dist}[i,v] \leftarrow \mathit{dist}[i-1, u] + w(u \rightarrow v)\)

以上が Bellman が示した最短路のアルゴリズムの本質的な部分です。この動的計画法のアルゴリズムを少しずつ変更していって先に示した \(\textsc{BellmanFord}\) に書き換える方法をこれから示します。まず、一番内側のループは各辺 \(u \rightarrow v\) を一回ずつ考えていますが、その順番は重要でないので、最後の三行のインデントを一つ無くすことができます。こうすることで辺を調べる順番が変わるかもしれませんが、それでも全ての \(i\) と \(v\) に対して \(\mathit{dist}_{\leq i} (v)\) が正しく計算されます。

procedure \(\texttt{BellmanFordDP2}\)(\(s\))

\(\mathit{dist}[0, s] \leftarrow 0\)

for 頂点 \(v \neq s\) do

\(\mathit{dist}[0,v] \leftarrow \infty\)

for \(i \leftarrow 1\) to \(V - 1\) do

for 頂点 \(v\) do

\(\mathit{dist}[i, v] \leftarrow \mathit{dist}[i - 1, v]\)

for \(u \rightarrow v\) の形をした辺 do

if \(\color{red}{\mathit{dist}[i, v] > \mathit{dist}[i-1, u] + w(u \rightarrow v)}\) then

\(\color{red}{\mathit{dist}[i,v] \leftarrow \mathit{dist}[i-1, u] + w(u \rightarrow v)}\)

次に最後の二行の添え字を \(i-1\) から \(i\) に変えます。これによって全ての \(i, v\)に対して \(\mathit{dist}[i,v] {\color{red}{ = }} \mathit{dist}_{\leq i} (v)\) ではなく \(\mathit{dist}[i,v] {\color{red}{\leq}} \mathit{dist}_{\leq i} (v)\) が成り立つようになるので、\(\mathit{dist}[i,v]\) が最短路の真の長さにより速く近づくようになります。この関係が成り立つのは命題 8.6 と命題 8.7 から分かります。

procedure \(\texttt{BellmanFordDP3}\)(\(s\))

\(\mathit{dist}[0, s] \leftarrow 0\)

for 頂点 \(v \neq s\) do

\(\mathit{dist}[0,v] \leftarrow \infty\)

for \(i \leftarrow 1\) to \(V - 1\) do

for 頂点 \(v\) do

\(\mathit{dist}[i, v] \leftarrow \mathit{dist}[i - 1, v]\)

for \(u \rightarrow v\) の形をした辺 do

⟨⟨\(i-1\) でない！⟩⟩

if \(\mathit{dist}[i, v] > \mathit{dist}[{\color{red}{i}}, u] + w(u \rightarrow v)\) then

\(\mathit{dist}[i,v] \leftarrow \mathit{dist}[{\color{red}{i}}, u] + w(u \rightarrow v)\)

しかし考えてみると、このアルゴリズムはすこし馬鹿なことをしています。というのも、外側のループの反復が \(\mathit{dist}[\ast, \ast]\) の \(i-1\) 行目を \(i\) 行目にコピーすることから始まり、その後 \(i\) 行目の要素しか使わないのです。つまり二次元配列は不必要で、反復のための添え字 \(i\) は余分です！最後の変更として、暫定的な距離を一次元配列だけを使って管理するようにします:

procedure \(\texttt{BellmanFordFinal}\)(\(s\))

\(\mathit{dist}{\color{red}{[s]}} \leftarrow 0\)

for 頂点 \(v \neq s\) do

\(\mathit{dist}{\color{red}{[v]}} \leftarrow \infty\)

for \(i \leftarrow 1\) to \(V - 1\) do

for \(u \rightarrow v\) の形をした辺 do

if \(\mathit{dist}{\color{red}{[v]}} > \mathit{dist}{\color{red}{[u]}} + w(u \rightarrow v)\) then

\(\mathit{dist}{\color{red}{[v]}} \leftarrow \mathit{dist}{\color{red}{[u]}} + w(u \rightarrow v)\)

最終的な動的計画法のアルゴリズムは \(\textsc{BellmanFord}\) の最初の定式化とほとんど同一です！最初の三行が最短路距離を初期化し、最後の二行が緊張した辺を緩和しています。\(\textsc{BellmanFordFinal}\) には前者へのポインタの管理と閉路の検出という機能がありませんが、幸いにもこの機能を追加するのは簡単です。

練習問題

辺に任意の重みが付いた、負閉路が含まれないとは限らない有向グラフを \(G\) とし、\(s\) を \(G\) の適当な頂点とします。
1. 全ての頂点 \(v\) が \(\mathit{dist}(v)\) を保持しているとします (前者へのポインタは保持していません)。このとき全ての \(v\) について \(\mathit{dist}(v)\) が \(s\) から \(v\) への最短路の長さかどうかを判定するアルゴリズムを説明、解析してください。
2. 全ての頂点 \(v \neq s\) が \(G\) の他の頂点へのポインタ \(\mathit{pred}(v)\) を保持しているとします (距離は保持していまません)。このとき前者へのポインタ全体が \(s\) を根とする単一ソース最短路木を定義するかどうかを判定するアルゴリズムを説明、解析してください。
ループ木 (looped tree) とは、木に葉から根に向かう辺を追加してできる重み付きの有向グラフのことを言います。辺の重みは非負とします。

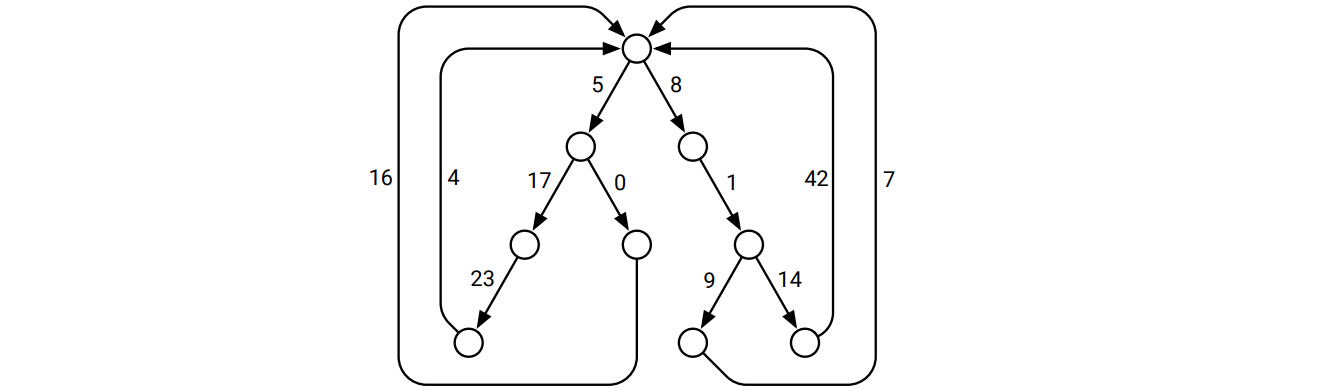ループ木
1. \(n\) 個の頂点を持つループ木に対して、Dijkstra のアルゴリズムを使って二つの頂点 \(u\) と \(v\) の間の最短路を計算するとどれくらいの時間がかかりますか？
2. Dijkstra のアルゴリズムよりも高速なアルゴリズムを説明、解析してください。
辺に重みの付いた有向グラフ \(G\) と二つの頂点 \(s, t\) が与えられたとします。
1. \(G\) がちょうど一つの負辺を持つときに、\(s\) から \(t\) への最短路を計算するアルゴリズムを説明、解析してください。 [ヒント: Dijkstra のアルゴリズムを変更するか、あるいは変更しないでください。]
2. \(G\) がちょうど \(k\) 個の負辺を持つときに、\(s\) から \(t\) への最短路を計算するアルゴリズムを説明、解析してください。アルゴリズムの実行時間は \(k\) にどのように依存しますか？
全ての頂点に正の重みが付いた無向グラフ \(G\) が与えられたとします。
1. \(G\) の全域木で重みが最小のものを見つけるアルゴリズムを説明、解析してください (全域木の重みとは含まれる頂点の重みの和です)。
2. 二つの頂点 \(s, t\) が与えられたときに、\(s\) から \(t\) への路で重みが最小のものを見つけるアルゴリズムを説明、解析してください (路の重みとは含まれる頂点の重みの和です)。
[ヒント: 片方の問題の答えは自明です。]
グラフ \(G\) とその辺 \(e\) に対して、\(G \backslash e\) で \(G\) から \(e\) を削除して得られるグラフを表すことにします。置換路問題 (replacement paths problem) とは、グラフ \(G\) と二つの頂点 \(s, t\) が与えられたときに、全ての辺 \(e\) に対して \(G \backslash e\) における \(s\) から \(t\) への最短路を計算する問題です。問題の答えは最短路の長さを収めた配列 \(E\) であり、\(E\) の添え字が取り除く \(G\) の辺に対応します。
1. \(G\) が有向グラフであり、\(G\) における \(s\) から \(t\) への最短路が \(G\) の全ての頂点を訪れるとします。この特殊ケースに対する置換路問題を \(O(E\log V)\) 時間で解くアルゴリズムを説明してください。
2. ❤ 任意の無向グラフに対する置換問題を \(O(E\log V)\) 時間で解くアルゴリズムを説明してください。
両方の問題において、辺の重みは非負であると仮定してください。 [ヒント: \(G\) における最短路の辺を削除した場合、元の最短路と新しい最短路はどのように重なりますか？]
\(G = (V, E)\) を辺に非負の重みが付いた有向グラフ、\(s, t\) を \(G\) の頂点、\(H\) を \(G\) からいくつかの辺を削除して得られるグラフとします。\(G\) から取り除いた辺を一つだけ \(H\) に戻して \(s\) から \(t\) への最短路の長さを最短にしたいとしたとき、戻すべき辺を \(O(E \log V)\) 時間で選択するアルゴリズムを説明、解析してください。
1. Bellman-Ford のアルゴリズムを改変して、 \(s\) から到達可能な負閉路がある場合にはその負閉路を返し、そのような負閉路が無い場合には最短路木を返すアルゴリズムを作ってください。またそのアルゴリズムの解析も行ってください。改変されたアルゴリズムの実行時間は \(O(VE)\) のままであるべきです。
2. Bellman-Ford のアルゴリズムを改変して、入力グラフに負閉路が含まれている場合でも \(s\) から他の全ての頂点への最短路を正しく計算するアルゴリズムを作ってください。つまり、アルゴリズムは \(s\) から \(v\) への負閉路を含む歩道が存在するなら \(\mathit{dist}(v) = -\infty\) とし、そうでないなら \(s\) から \(v\) への最短路の長さを \(\mathit{dist}(v)\) に代入します。アルゴリズムの解析も行ってください。改変されたアルゴリズムの実行時間は \(O(VE)\) のままであるべきです。
3. ❤ (a) と (b) を Ford の一般的な緩和アルゴリズムに対して解いてください。改変されていない Ford のアルゴリズムが負辺を含まないグラフに対しては \(O(2^{V})\) ステップで停止することを既知として構いません。改変されたアルゴリズムの実行時間も \(O(2^{V})\) であるべきです。
次に示す、さらに意味の曖昧な Ford の一般的な緩和アルゴリズムの変種を考えます:

procedure \(\texttt{FellmannBored}\)(\(s\))

\(\texttt{InitSSSP}\)(\(s\))

while 飽きるまで do

\(e_{i} \leftarrow G\) の適当な辺

if \(e_{i}\) が緊張している then

\(\texttt{Relax}\)(\(e_{i}\))

\(s\) を始点とする適当な歩道 \(W\) の辺を順番にチェックしていった場合、\(W\) の最後の辺につけられる距離のラベルは \(W\) の長さ以下であることを示してください。きちんと言うと: 任意の歩道 \(s = v_{0} \rightarrow v_{1} \rightarrow \cdots \rightarrow v_{l}\) について、辺をこの順番で調べていったときに \(\mathit{dist}(v_{l}) \leq \sum_{i=1}^{l} w(v_{i-1} \rightarrow v_{i})\) であることを示してください。 [ヒント: この命題を証明することは正しく主張することよりも簡単なぐらいです。]
この問題では Ford の一般的な緩和アルゴリズムを使って負閉路を検出する方法について考えます。
1. \(\mathit{pred}(s)\) が \(\textsc{InitSSSP}\) の後に一度でも変更されるならば、入力グラフに \(s\) を通る負閉路が含まれることを示してください。
2. 入力グラフに \(s\) を通る負閉路が含まれていたとしても \(\mathit{pred}(s)\) が \(\textsc{InitSSSP}\) の後に一度も変更されない場合があることを示してください。
3. 前者への辺 \(\mathit{pred}(v) \rightarrow v\) の集合からなるグラフを \(P\) とし、緊張している辺の集合を \(X\) とします。\(P\) と \(X\) はどちらもアルゴリズムの実行が進むにつれて変化します。グラフが閉路を含まないのは \(P \cup X\) が常に DAG である場合に限ることを示してください。
4. これまでに緩和された辺の集合を \(R\) とします。\(R\) はアルゴリズムの実行が進むにつれて変化します。グラフが閉路を含まないのは \(R\) が常に DAG である場合に限ることを示してください。
❤ 辺の重みが負でもあり得る場合、DAG に対する Dijkstra のアルゴリズムが最悪ケースで \(\Theta(2^{V})\) 回の緩和を行うことを示してください。具体的には、任意の正の整数 \(n\) に対して、Dijkstra のアルゴリズムが \(\textsc{Relax}\) を \(\Theta(2^{n})\) 回呼ぶ \(n\) 頂点の重み付きDAG \(G_{n}\) を構築してください。 [ヒント: バイナリカウンタ]
❤ 入力グラフが負閉路を持たないならば、Ford の一般的な緩和アルゴリズムが (したがって Dijkstra のアルゴリズムも) 最大でも \(O(2^{V})\) 回の緩和の後に停止することを示してください。 [ヒント: 問題 9.9.(d)]
有向グラフ \(G\) が与えらたとします。\(G\) はソース \(s\) を持っていて、さらに全ての辺に負の重み ("長さ") が付いているとします。このとき \(s\) から他の全ての頂点への最短経路の長さを計算する効率の良いアルゴリズムを説明、解析してください。つまり、全ての頂点 \(t\) に対して次の仕様を満たすアルゴリズムを説明してください:
- \(t\) に \(s\) から到達できないなら、アルゴリズムは \(\mathit{dist}(t) = \infty\) を出力する。
- \(G\) が \(s\) から到達できる閉路を持ち、その閉路から \(t\) に到達である場合、\(s\) から \(t\) への路 (正しくは歩道) の長さは任意に小さな負の値を取れるので、最短経路の距離が定義できなくなる。この場合のアルゴリズムは \(\mathit{dist}(t) = -\infty\) を出力する。
- 二つのどちらでもない場合、アルゴリズムの出力は \(s\) から \(t\) への最短経路の長さを正しく出力する。
これまで考えてきたのは二つの頂点の間の "唯一の" 最短路 ("the" shortest path) でしたが、一つグラフの中に同じ頂点を結ぶ最短路が複数あることがあります。そのような場合、重み付きグラフに対する問題であっても、重みが最小の路の中で辺の一番少ないものを選ぶのが望ましいことが多いです。このような路を \(s\) から \(t\) への最良路 (best path) と言います。辺に正の重みが付いた有向グラフ \(G\) とソース頂点 \(s\) が与えられたとします。\(G\) における \(s\) から他の頂点への最良路を計算するアルゴリズムを説明、解析してください。

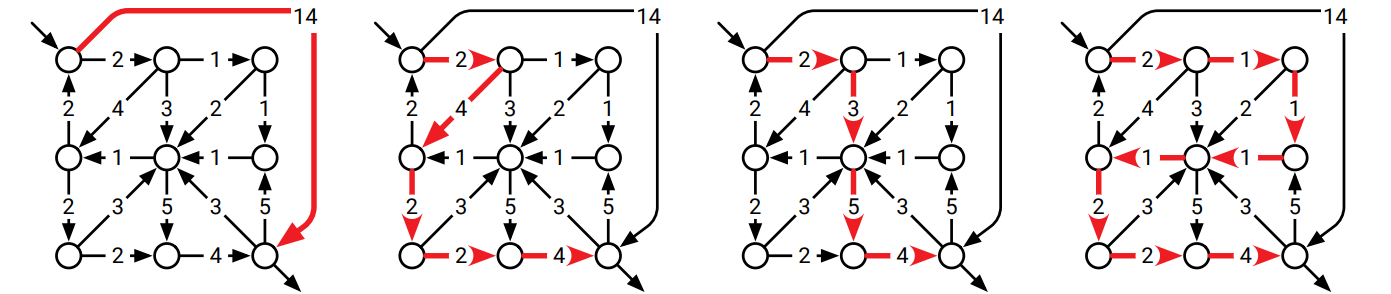図 8.18

長さの等しい四つの最短路 (最短路は他にもある)。一番左の路が「最良」の最短路である。
辺に重みの付いた有向グラフ \(G\) において、頂点 \(s\) から頂点 \(t\) への最短路の数を計算するアルゴリズムを説明、解析してください。辺の重みは正であり、算術演算は \(O(1)\) で行えると仮定して構いません。 [ヒント: \(s\) から他の全ての頂点に対する最短路の長さを計算し、\(s\) から他の頂点への最短路に含まれない辺を全て取り除きます。何が残りますか？]
あなたは小学校時代の親友を Twitbook で見つけました。あなたも相手もすぐにでも会いたいと思っているのですが、二人は遠くは離れた都市に住んでいます。旅行の時間を最小化するために、二人はお互いの住む都市の中間にある都市で会うことにしました。二人はそう決めてすぐに車に乗り込みましたが、さて、正確にどこで会えばよいのでしょうか？

重み付きグラフ \(G=(V,E)\) が与えられ、頂点 \(V\) が都市を、辺 \(E\) が都市の間を結ぶ道路を表します。全ての辺 \(e\) には重み \(w(e)\) が付いており、二つの都市の間を車で移動するのにかかる時間を表します。加えてあなたのスタート地点を表す頂点 \(p\) と相手のスタート地点を表す頂点 \(q\) が与えられます。

あなたと親友が一番早く会うことができる頂点 \(t\) を見つけるアルゴリズムを説明、解析してください。
あなたは Giggle Highway View プロジェクトのサイクリストとして雇われました。このプロジェクトでは米国の国立高速道路の写真をストリートごとに撮影します。試験的な実験として、あなたはオレゴン州ポートランドの "Giggleplex" からニューヨーク州ブルックリン区ウィリアムズバーグの "Gigglesburg" まで Giggle Highway-View 固定ギアカーボンファイバー自転車を走らせることになりました。

あなたは救いようのないカフェイン中毒なのですが、他の Giggle の従業員と同じようにコーヒーオタクでもあります: あなたが飲めるのは、日陰で育てられたオーガニックの豆を直接取引したものを、一種類だけ手で挽いて個別に焙煎して作ったエスプレッソに混じりけの無いミルクと砂糖を入れたものだけです。どうもありがとう。エスプレッソを補給すると、あなたはカフェイン離脱性片頭痛で苦しまずに自転車で \(L\) マイル進むことができます。

親切なことに、Giggle は全米中のコーヒーショップを表した無向グラフをあなたに渡してくれました。このグラフの頂点は日陰で育てられたオーガニックの豆を直接取引したものを、一種類だけ手で挽いて個別に焙煎して作ったエスプレッソを飲めるコーヒーショップを表し、辺がそれらを結ぶ高速道路を表します。各辺 \(e\) は高速道路の長さを表すラベル \(l(e)\) が付いています。二つの Giggle オフィスは頂点 \(s, t\) で表され、当然そこにはエスプレッソスタンドがあります。
1. Giggleplex から Gigglesburg までカフェイン離脱性片頭痛に苦しむことなく行けるかどうかを判定するアルゴリズムを説明、解析してください。
2. 値の張るソフト帽をかぶることで、エスプレッソを補給してから自転車で進むことができる距離 \(L\) を増やせることをあなたは発見しました。Giggleplex から Gigglesburg までカフェイン離脱性片頭痛に苦しむことなく行くために必要となる最小の \(L\) の値を求めるアルゴリズムを説明、解析してください。
3. 自転車で向こうのオフィスまで行くのが不可能であると (最近ライバル企業 Ünter から引き抜かれた) 上司に報告すると、彼女は地図を見せるように言いました。「あぁ、何が問題なのか分かったわ。地図にスターバックスが載ってないじゃない！」恐れおののくあなたに、彼女は全米中のスターバックスの場所を頂点として追加したグラフ \(G^{\prime}\) を渡しました。親切にも新しい頂点はスターバックスグリーン (Pantone® 3425 C) で塗られていました。
  
  Giggleplex から Gigglesburg までカフェイン離脱性片頭痛に苦しむことなく行くときに、訪れなければならないスターバックスの数を最小値を求めるアルゴリズムを説明、解析してください。きちんと言うと、アルゴリズムの出力は \(s\) から \(t\) への長さが \(L\) 以下の辺だけを使う路の中に含まれる緑の頂点の数の最小値です。
辺に非負の重みが付いた有向グラフ \(G = (V, E)\) と二つの頂点 \(s, t\) が与えられたとします。\(G\) に含まれる \(s\) から \(t\) への辺の数が \(3\) で割り切れる歩道のうち最短のもの見つけるアルゴリズムを説明、解析してください。

例えば、辺の重みが全て \(1\) である上のグラフに対するアルゴリズムの答えは、歩道 \(s \rightarrow w \rightarrow y \rightarrow x \rightarrow s \rightarrow w \rightarrow t\) に対応する \(6\) です。
辺に非負の重みが付いた有向グラフ \(G = (V, E)\) が与えられ、全ての辺が赤または青に塗られているとします。\(G\) における頂点 \(s\) から頂点 \(t\) への同じ色の辺が三回以上連続しない最短の歩道の長さを計算するアルゴリズムを説明してください。つまり、歩道が二回連続して赤い辺を通ったら次の辺は青い必要があり、歩道が二回連続して青い辺を通ったら次の辺は赤い必要があるということです。

例えば入力が次のグラフで赤い辺の重みが 1、青い辺の重みが \(2\) だった場合、アルゴリズムの出力は \(s \color{red}{\,\rightarrow}\) \(a \color{red}{\,\rightarrow}\) \(b \color{#2D2F91}{\,\Rightarrow}\) \(d \color{red}{\,\rightarrow}\) \(c \color{#2D2F91}{\,\Rightarrow}\) \(a \color{red}{\,\rightarrow}\) \(b \color{red}{\,\rightarrow}\) \(t\) に対応する \(9\) です。
辺に非負の重みが付いた有向グラフ \(G = (V, E)\) が与えられ、\(G\) の全ての辺が赤、白、青のどれかで塗られているとします。\(G\) の歩道に含まれる辺の色が赤、白、青、赤、白、青、という順番になっているとき、その歩道をフランス国旗歩道と呼びます。きちんと言うと、歩道 \(v_{0} \rightarrow\) \(v_{1} \rightarrow\) \(\cdots \rightarrow\) \(v_{k}\) がフランス国旗歩道なのは、全ての整数 \(i\) について、辺 \(v_{i} \rightarrow v_{i+1}\) の色が \(i \mod 3 = 0\) ならば赤、\(i \mod 3 = 1\) ならば白、\(i \mod 3 = 2\) ならば青な場合です。

開始頂点 \(s\) から \(G\) の他の全ての頂点に対する最短のフランス国旗歩道を計算するアルゴリズムを説明してください。
\(n\) 個の銀河を結ぶ \(m\) 個の銀河間テレポートウェイがあります。各テレポートウェイは二つの銀河を結んでいて、双方向に使うことができます。また各テレポートウェイ \(e\) の運賃は \(c(e)\) ドルであり、\(c(e) > 0\) です。同じテレポートウェイを複数回使っても構いませんが、使うたびに運賃を支払う必要があります。

Judy は銀河 \(s\) から銀河 \(t\) までなるべく安く移動したいと思っています。しかし彼女は小銭を持ち歩きたくないので、運賃の合計を 5 ドルの倍数にしたいとも考えています。
1. 運賃の合計が 5 ドルの倍数でなければならないという制約の下で \(s\) から \(t\) まで移動するときの最小の合計運賃を計算するアルゴリズムを説明、解析してください。
2. Judy が一回だけテレポートを無料にできるクーポンを持っているとして (a) を解いてください。
新しい街に引っ越してきたあなたは、自宅から仕事場までの徒歩の通勤ルートを決めることにしました。毎日運動ができるように、このルートは最初の部分が登り道 (運動用) で残りの部分が下り道 (休憩用) であるか、そうでなければ全てが登り道あるいは全てが下り道である必要があります (仕事場から自宅への帰り道にも同じ道を使うので、この場合でも運動ができます)。一方で仕事場に遅刻しないように、この条件を満たすルートの中で最短のものを選ぶ必要があります。

問題の入力は無向グラフ \(G\)、開始頂点 \(s\)、目標頂点 \(t\) であり、\(G\) の頂点が交差点を、辺がそれらを結ぶ道路を表します。各頂点 \(v\) には交差点の海抜を表す値 \(h(v)\) が、各辺 \(e\) には道路の長さを表す値 \(l(e)\) が付いています。
1. 全ての頂点の高さが異なる場合に、\(s\) から \(t\) への最短の "登って下る" 路を求めるアルゴリズムを説明、解析してください。
2. 頂点の高さが同じことがある場合に、\(s\) から \(t\) への最短の "登って下る" 路を求めるアルゴリズムを説明、解析してください。高さが変化しない辺は "登る" 部分と "下る" 部分のどちらで使っても構いません。
3. \(s\) から \(t\) への条件を満たす路が存在しないとします。\(s\) から \(t\) の路であって "登る" 道と "下る" 道の入れ替わりの回数が最小な路を考えたときに、その中で長さが最小のものを求めるアルゴリズムを説明してください。
Sham-PooBanana 大学を卒業したあなたは、飛行機が大嫌いな人のための旅行会社 Aerophobes-Я-Us に就職しました。あなたの仕事はある都市から別の都市へのフライトのプランを顧客に提示するシステムの作成です。顧客はみな飛行機での移動 (そして空港にいること) を嫌うので、プランに含まれるフライトはできるだけ短い必要があります。あなたは地球上の全てのフライトの発着時間にアクセスできるとします。

ある顧客が都市 \(X\) から都市 \(Y\) まで飛行機で移動したいとします。移動にかかる合計時間、つまり最初のフライトの出発時間から最後のフライトの到着時間までの、別のフライトを待つ時間も含めた時間が最小になるようなフライトの列を求めるアルゴリズムを説明してください。
練習問題 5.20 では鋭角迷路が解けるかどうかを判定するアルゴリズムを考えました。この問題では、与えられた鋭角迷路を通り抜ける最短経路を見つける問題を三つ異なる "長さ" に対して考えます。

鋭角だけが含まれる線で Start と Finish をつなぎましょう。

アルゴリズムには連結無向グラフ \(G\) が与えられ、頂点が平面上の点に、辺が線分に対応します。辺は端点以外の点で交わりません。例えば X の形をした迷路には 5 個の頂点と 4 個の辺が含まれ、上図左の迷路には 18 個の頂点と 21 個の辺が含まれます。アルゴリズムには二つの頂点 \(\textsc{Start}\) と \(\textsc{Finish}\) も与えられます。

\(G\) に含まれる歩道が鋭角歩道としての条件を満たすのは、歩道の連続する任意の二つの辺 \(u \rightarrow v \rightarrow w\) について \(\angle uvw = \pi\) または \(\angle uvw < \pi / 2\) なときです。辺を二つ受け取ってそれらが直線か、鈍角か、鋭角かを \(O(1)\) 時間で判定するサブルーチンを使えると仮定してください。
1. \(\textsc{Start}\) と \(\textsc{Finish}\) への条件を満たす路の中で線分の数が最小になるものを計算するアルゴリズムを説明してください。
2. \(\textsc{Start}\) と \(\textsc{Finish}\) への条件を満たす路の中で方向転換の数が最小になるものを計算するアルゴリズムを説明してください。 [ヒント: この問題は (a) と同じではありません]
3. \(\textsc{Start}\) と \(\textsc{Finish}\) への条件を満たす路の中で辺のユークリッド距離が最小になるものを計算するアルゴリズムを説明してください。任意の線分の長さを \(O(1)\) 時間で計算できるとしてください。
See-Bull Center for Fake News Detection で行われた難しい中間試験を終えて、あなたはバスで家に帰ろうとしています。バスで帰ることになると分かっていたので、あなたは Sham-PooBanana の街の中を走る全てのバスがいつどの停留所に停まるかをまとめた表を持っています。残念ながら See-Bull Center から自宅まで直接行くバスはないので、最低でも一度はバスを乗り換える必要があります。全部で \(b\) 台のバスが走っており、全てのバスは 12:00:01 AM に出発し、\(n\) 個の停留所を回り、11:59:59 PM に最後の停留所に停まります。バスはスケジュールに従って正確に運行され、あなたは正確な時計を持っています。またあなたは疲れ切っているので停留所の間を歩くことはできません。
1. 家になるべく早く着くようなバスの列を計算するアルゴリズムを説明、解析してください。最小化するのは到着時間であって、See-Bull Center から家まで行くのにかかる時間ではありません。
2. 大変です！中間試験はハロウィーンに行われたので、道がゾンビであふれています！残念ながら、Sham-PooBanana の公共交通機関担当の部署には一年のうちたった一夜のためにバスを追加したりゾンビお断りのバス停留所を設置したりするための予算がありません。バスの停留所で過ごす時間を最小化するようなバスの列を計算するアルゴリズムを説明、解析してください。家に着くのが遅くなったり、バスに乗っている時間が長くなったりしても構いません。また最初にバスに乗るまでは See-Bull Center で安全に待つことができるので、最初のバスに乗るまでの時間はカウントしません。
夢のような春休みから帰った次の朝、Alice が目覚めると車が動かなくなっていました。彼女は Sham-PooBanana 大学の講義に公共交通機関を使って出席しなければなりません。PooBanana 地方のバスの完全な運行表を彼女は持っています。運行表の中でバスの運行ルートは有向グラフ \(G\) で表され、頂点が停留所を、辺がそれらの間の運行ルートを表します。各辺 \(u \rightarrow v\) について、運行表には次に示す三つの正の実数が書かれています:
- \(l(u \rightarrow v)\) は停留所 \(u\) から停留所 \(v\) へのバスを使った移動にかかる時間 (分) を表す。
- \(f(u \rightarrow v)\) は停留所 \(u\) から停留所 \(v\) に向かって出発するバスの最初の出発時間 (12:00 AM からの相対時刻) を表す。
- \(\Delta(u \rightarrow v)\) は停留所 \(u\) から停留所 \(v\) に向かって出発する二つの連続するバス同士の出発時間の間隔 (分) を表す。
つまり、\(u\) を \(v\) に向かって最初に出発するバスは時刻 \(f(u \rightarrow v)\) に \(u\) を出発し、時刻 \(f(u \rightarrow v) + l(u \rightarrow v)\) に \(v\) に到着します。同じ区間の二本目のバスは時刻 \(f(u \rightarrow v) + \Delta(u \rightarrow v)\) に \(u\) を出発し、\(f(u \rightarrow v) + \Delta(u \rightarrow v) + l(u \rightarrow v)\) に \(v\) に到着します。三本目のバスは時刻 \(f(u \rightarrow v) + 2 \cdot \Delta(u \rightarrow v)\) に \(u\) を出発し、\(f(u \rightarrow v) + 2 \cdot \Delta(u \rightarrow v) + l(u \rightarrow v)\) に \(v\) に到着します。

Alice が目的地に着くことができる一番早い時刻を求めるアルゴリズムを説明、解析してください。アルゴリズムの入力はグラフ \(G = (V, E)\) と頂点 \(s, t\) 、各辺 \(e \in E\) に対する \(l(e), f(e), \Delta(e)\) の値、そして Alice が家を出る時間 (12:00 AM からの相対時刻) です。

[ヒント: このレアなインスタンスでは、入力グラフを改変するよりもアルゴリズムを改変した方が簡単かもしれません。]
Mulder と Scully はアメリカ中の全ての道路について、その道路を車で走っている人がエイリアンに誘拐される確率を正確に計算しました。そして Mulder 捜査官はバージニア州 Langley からネバダ州の Area 51 まで車で移動することになりました。どうすればエイリアンに誘拐される確率を最小化できるでしょうか？

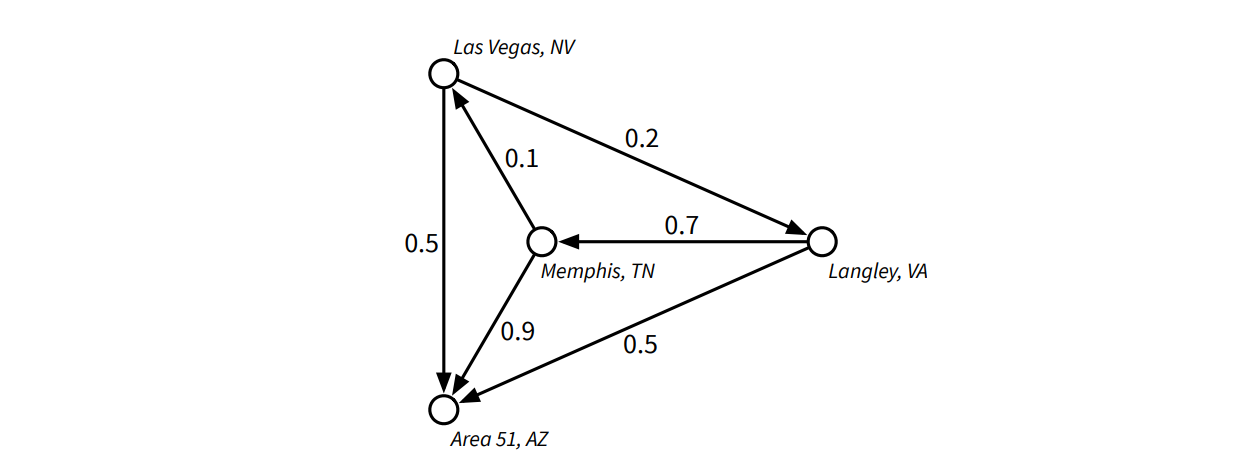
きちんと問題を定義すると、グラフ \(G = (V, E)\) が与えられ、各辺 \(e\) が安全さを表す互いに独立な確率 \(p(e)\) を持っているとします。\(G\) の路の安全性をその辺の安全性の積と定義したときに、与えられた頂点 \(s\) から \(t\) への路の中で最も安全性の高いものを計算するアルゴリズムを説明、解析してください。必要になる算術演算は全て \(O(1)\) 時間で実行できるとしてください。

例えば道路と確率が上図のようになっている場合、Mulder が Langley から Area 51 に直接行った場合は 50 % の確率で誘拐されずにたどり着くことができます。また Memphis を経由していけば、0.7 × 0.9 = 63 % の確率で安全にたどり着けます。しかしもし Memphis と Las Vegas を経由するようにした場合、彼は 1 - 0.7 × 0.1 × 0.5 = 96.5 % の確率で (Elvis のように) 誘拐されてしまいます！
♣ Sunnydale 国立公園で行われた宿泊キャンプ旅行で、あなたは叫び声を聞いて落ち着かない眠りから目を覚ましました。何が起きたのかとテントの周りを探っていると、森の中から怯え切った血まみれの公園の警備員がくしゃくしゃの紙を胸に抱えて走ってきました。彼はあなたのテントに近づくと、「逃げろ......るうちに...」という言葉と共に紙をあなたに渡し、そのまま倒れてしまいました。脈を調べたところ、その警備員は完全に息を引き取っていました。

渡された紙を確認すると、その紙が公園の地図であることが分かりました。地図は無向グラフであり、頂点が公園の目印となるものを、辺がそれらの間の歩道を示しています (歩道は頂点同士をつなぐだけで、重なったりしません)。あなたは自分が今いる頂点を見つけることができました。地図の端にある頂点のいくつかには EXIT の印が付いています。

紙をさらによく調べると、誰か (おそらくは今死亡した哀れな公園警備員) によって頂点と辺に \(0\) から \(1\) の実数が書かれていることに気が付きました。地図の裏に走り書きされたメモによると、辺に書かれた数値は対応する歩道を歩いているときに怪物に襲われる確率であり、頂点に書かれた数値は対応する目印にいるときに怪物に襲われる確率であるようです (怪物は必ず単独で行動するので、同時刻に同じ歩道および目印に二匹以上の怪物がいることはありません)。紙には辺で示した歩道から出るとゆっくりとした悲惨な死が待っているという警告もあります。

あなたは足元の死体に目をやりました。確かに彼の死は悲惨というほかありません。待てよ、今動いたか？歯が伸びていっていないか？あなたはテントの杭を死体の心臓に突き刺して、頭をフル回転させて最短経路で公園から逃げることを決めました。

現在位置から適当な出口までの路の中で怪物との遭遇回数の期待値が最小になるものを求める効率の良いアルゴリズムを説明、解析してください。 [ヒント: 頂点に確率が無かったとしても、この問題は前問と同じではありません！]

West on Church, north on Prospect, east on I-74, south on I-465, east on Airport Expressway, north on I-65, east on I-70, north on Grandview, east on 5th, north on Olentangy River, east on Dodridge, north on High, west on Kelso, south on Neil. Depending on traffic. 今は二人で Urbana に住んでいます。^[return]
正確に言えばここで議論しているのは最短路 (shortest path) ではなくて最短歩道 (shortest walk) です。しかしこの用語の乱用は通例となっています。用語を正確に使って議論すると、\(s\) が \(t\) に到達できるなら、\(s\) から \(t\) への最短単純路が存在します。ただ計算するのは (負閉路がある場合には、ハミルトン路問題からの簡単な帰着によって) NP 困難です。一方で、\(s\) から \(t\) への最短歩道が存在するならば、その歩道は単純路であり、もちろん \(s\) から \(t\) への最短の単純路です。ああややこしい。^[return]
正確に言うと、Danzig は最短路問題が線形計画問題として表現できることを示し、それから彼が考案した単体法を元のグラフの言葉を使って説明しました。彼の説明は Ford の緩和を使った戦略と (事実上) 同じです。^[return]
Moore を動機付けたのは、Claude Shannon (クロード・シャノン) が 1950 年に設計・作成した迷路を解くロボット「テセウス (Theseus)」の弱点でした (テセウスは電気機械式のリレーで実装されたメモ化付きの深さ優先探索を使っていました。これがグラフにおける深さ優先探索の初めての実装であることはほぼ間違いないでしょう)。Moore によると: 「解が二つ以上ある迷路に対してこの機械を動かすのを見せると、ある訪問者が「なぜこの機械は最短路を答えないことがあるのか」と聞いてきた。そこで Shannon と私はこの問題を機械で解く安価な方法を研究した。彼はアナログ計算に適した方法をいくつか見つけ、私はこれらのアルゴリズムを思いついた」⁵^[return]
迷路を通り抜ける最短路を見つけるアナログな方法として提案されたものには、ボールベアリング、液体/プラズマの流れ、化学反応の波、走化性、レジスタネットワーク、LED の付いた電子回路、メモリスタのネットワーク、マイクロ流体力学チップ内のグロー放電、植物の育成、粘菌、アメーバ、アリ、蜂、線虫、そして観光客があります。^[return]
Konrad Zuse は初期のコンピューティングのパイオニアの一人です。 1930 年代後半、彼は (後に Z1 と名付けられる) 自身初のプログラム可能なコンピューターを両親のリビングルームにおいてあった金属の棒とストリップから作成しました。しかしオリジナルの Z1 とその設計図は 1944 年の英国の空襲によって破壊されてしまいます。Zuse の 1945 年の博士論文には Plankalkül (プランカルキュール) と呼ばれる世界初の高レベルプログラミング言語が示されています。Zuse の博士論文に含まれる Plankalkül プログラムの最初の完全な例は幅優先探索を使ってグラフの成分を数える処理の実装であり、疑似コードによる説明と 8 頂点の非連結グラフに対するアルゴリズムの実行例がステップごとに図示されています。ナチス政権が崩壊したために Zuse は博士論文を提出できず、 Plankalkül は 1972 年まで公表されませんでした。Plankalkül の初の実装が Joachim Hohmann (ヨアキム・ホーマン) によって発表されたのはようやく 1975 年のことです。^[return]
歴史的に不正確なのは承知で、私はこの慣習に従います。 "Leyzorek-Gray-Johnson-Ladew-Meaker-Petry-SeitzDantzig-Dijkstra-Minty-Whiting-Hillier のアルゴリズム" と書かれているのを読みたい人はいないでしょうし、実際に出版されなかった論文というのは発見とみなされないからです。^[return]
1950 年代の最短路に関する論文は優先度付きキューに全く言及していません。Dijkstra が提案したのは一番外側の波面にある全ての頂点を各反復で総当たりで調べる方法です。このアルゴリズムの実行時間は \(\pmb{O(V^{2})}\) であり、\(E = \Omega(V^{2})\) の場合には二分ヒープを使った実装よりも高速です！Minty が提案したのは辺 \(u \rightarrow v\) であって \(\mathit{dist}(u)\) が有限かつ \(\mathit{dist}(v)\) が無限のものに対する総当たりであり、この場合の実行時間は \(O(VE)\) です。二分ヒープとして実装された優先度付きキューを使ったほぼ線形の実行時間を最初に示したのは Donald Johnson (ドナルド・ジョンソン) で、1977 年のことです。フィボナッチヒープと呼ばれるさらに複雑な優先度付きキューのデータ構造を使えば実行時間を \(\pmb{O(E+ V \log V)}\) まで改善できます。またさらに洗練された優先度付きキューを使えば、辺の重みが特殊な場合に対する高速なアルゴリズムを作ることができます。^[return]
面白いことに、Shier と Witzgall の例は辺が \(O(V)\) 個しか含まれない DAG です。よって仮にジグザグな路が最短路木であることを知らなかったとしても、最短路は (他の最短路アルゴリズムを使って) \(O(V)\) 時間で計算できてしまいます。^[return]
歴史的に不正確なのは承知で、私はこの慣習に従います。 "Shimbel / Moore / Woodbury-Dantzig / BellmanFord / Kalaba / Minty のアルゴリズム" と書いてあるのを読みたい人はいないでしょうし、"Shimbel's algorithm" について話していると相手が不思議な目でこちらを見てくるのはもうごめんです。^[return]
この名前が指しているのは Richard Bellman と Robert Kalaba (ロバート・カラバ) によって 1956 年に書かれた動的計画法と制御理論に関する専門書のことで、Bellman のアルゴリズムがこの本で説明されています。Bellman と Kalaba は任意の \(k\) に対して \(k\) 番目に短い路を計算する Bellman のアルゴリズムを拡張したアルゴリズムを 1960 年に発表しています。^[return]
Hyperbole and a Half をもう一度全部読んでください。それから新しく猫を引き取って、もう一冊本を買えるようにしてください。^[return]
このチェックをしなくても Moore のアルゴリズムは正しく動きますが、このチェックをしないと \(O(VE)\) の実行時間が保証されなくなります。^[return]
次の章で見ますが、このパラメータが唯一の選択肢というわけではありません。^[return]