フローの合成と分解

証明 \(f\) に含まれるゼロでないフローを持つ辺の数に関する帰納法で示す。直感的に言うと、Ford-Fulkerson のアルゴリズムを逆回しにしたのがこの証明である。

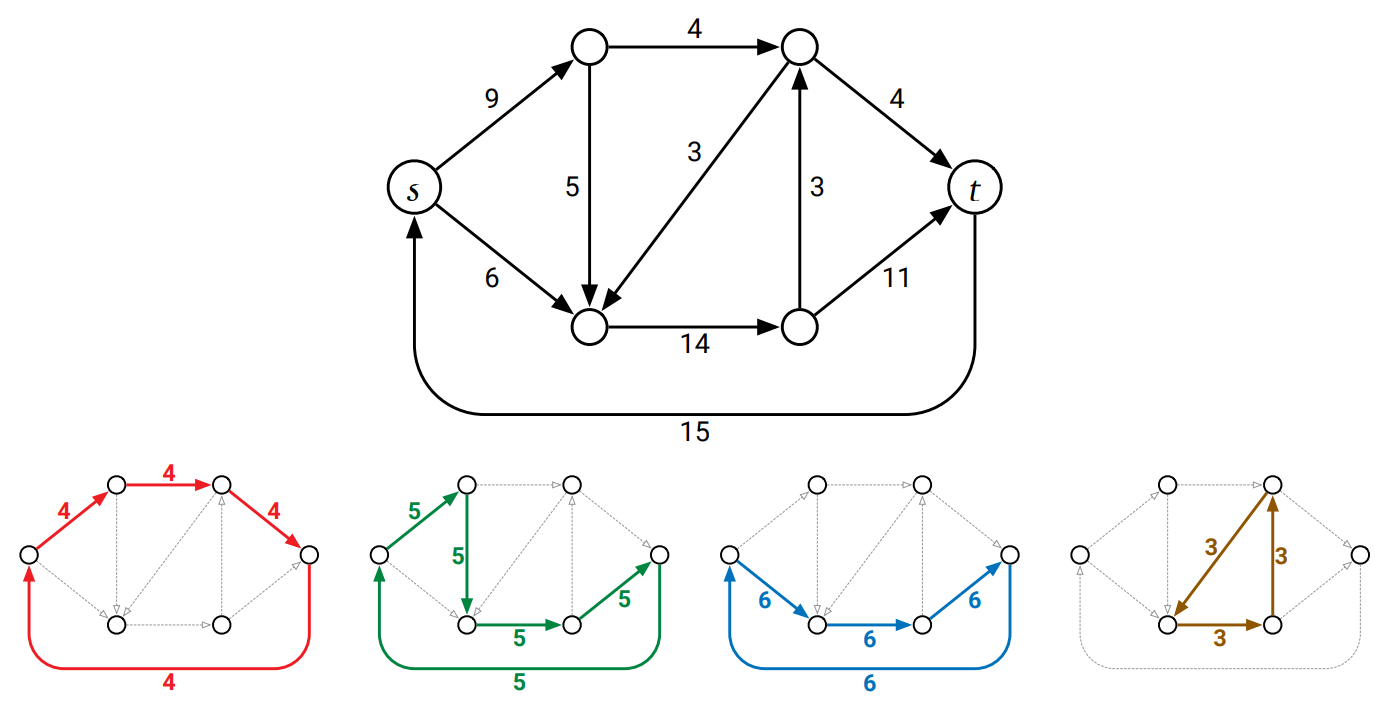
\(f\) において少なくとも一つの辺が正のフローを持っているならば、その辺を通る \((s,t)\)-路あるいは負閉路が存在する。よってその路または閉路を \(f\) から引けるだけ引くことで少なくとも一つの辺を \(f\) から消すことができる。こうするとゼロでないフローを持つ辺の数が減るので、あとは再帰の妖精が残りの分解をしてくれる。

この議論をきちんと行うために、 \(f\) が循環 (circulation) である特殊ケースを考える。フローが循環であるとは、値が \(0\) で \(s,t\) を含む全ての頂点において保存条件が成り立つことを言う。任意のフローネットワークとそれに含まれる循環 \(f\) を固定し、\(f(u \rightarrow v) > 0\) を満たす辺 \(u \rightarrow v\) の数を \(\#f\) とする。\(f\) が最大でも \(\max \lbrace 0, \# f - 1 \rbrace\) 個の閉路の正の線形結合に分解できることを、これから \(\# f\) に関する帰納法で示す。考えるべきケースは三つある:

• \(\# f = 0\) の場合、\(f\) はゼロ個の閉路の線形結合である。

• \(f (u \rightarrow v) > 0\) である辺 \(u \rightarrow v\) 全体が有向閉路を作る場合、\(f\) は一つの閉路の線形結合として表せる。

• そうでない場合、\(f(u \rightarrow v) > 0\) である辺 \(u \rightarrow v\) について、任意の歩道 \(u = v_{0} \rightarrow\) \(v = v_{1} \rightarrow\) \(v_{2} \rightarrow \cdots \) であって全ての添え字 \(i\) について \(f(v_{i-1} \rightarrow v_{i} ) > 0\) であるものを考える。フローの保存条件から全ての頂点に出るフローと入るフローがあるので、この歩道は任意に長くできる。そうした場合二回以上訪れる頂点が存在するので、そのような頂点で一番添え字が若いものを \(v_{j} = v_{k}\) \((j < k)\) とする。このとき \(v_{j} \rightarrow v_{j-1} \rightarrow \cdots \rightarrow v_{k}\) は単純閉路 \(C\) となる。

  \(\displaystyle F := \min_{e \in C} f(e)\) とし、新しい関数 \(f^{\prime}\) を \(f^{\prime} := f - F \cdot C\)、省略せずに書くと \[ f^{\prime}(u \rightarrow v) := \begin{cases} f(u \rightarrow v) - F & \text{if } u \rightarrow v \in C \\ f(u \rightarrow v) & \text{それ以外} \end{cases} \] と定義する。定義を追っていくと \(f^{\prime}\) は値が \(0\) で実現可能な \(G\) の循環であることが分かる。\(F\) の定義よりある \(e \in C\) において \(f(e) = F\) となるので、その \(e\) に対して \(f^{\prime}(e) = 0\) であり、したがって \(\# f^{\prime} \leq \# f - 1\) である。\(f^{\prime}\) は \(f\) より少ない辺しか持たないことから、帰納法の仮定より \(f^{\prime}\) には \(\# f^{\prime} - 1 \leq \# f - 2\) 個以下の閉路を使った分解が存在する。よってこの分解に \(C\) に沿って \(F\) だけフローを流したフローを追加すれば、\(\# f - 1\) 個の路または閉路を使った \(f\) の分解が手に入る。このことを簡潔に書けば \(f = f^{\prime} + F \cdot C\) である。

以上より \(f\) が最大でも \(\max \lbrace 0, \# f - 1 \rbrace\) 個の閉路の正の線形結合に分解できることが示せた。

\(f\) を任意のフローネットワークに対する \(|f| > 0\) を満たす任意の \((s,t)\)-フローとする。ネットワークに \(t \rightarrow s\) という辺を追加し、新しい循環 \(f^{\prime}\) を \(f^{\prime} (t \rightarrow s) = |f|\) およびそれ以外の辺に対しては \(f^{\prime} (u \rightarrow v) = f(u \rightarrow v)\) として定義する。ここで \(\# f^{\prime} = \# f + 1 \geq 2\) である。前述の議論より \(f^{\prime}\) は最大でも \(\#f^{\prime} - 1\) 個の有向閉路の正の線形結合に分解できる。この分解から辺 \(t \rightarrow s\) を取り除いたときに得られるのはフロー \(f\) に対する分解であり、最大でも \(\# f^{\prime} - 1 \leq \# f\) 個の \((s,t)\)-路および閉路しか持たない。具体的には、\(f^{\prime}\) における \(s \rightarrow t\) を含む閉路は \(f\) における \((s,t)\)-路となり、\(f^{\prime}\) における \(s \rightarrow t\) 閉路を含まない閉路は \(f\) においても閉路のままとなる。 \(\Box\)