唯一の全域最小木アルゴリズム

最小全域木を計算するアルゴリズムはたくさんありますが、そのほとんどはこれから説明する一般的な戦略のインスタンスと言うことができます。これはグラフ探索アルゴリズムにおいて、たくさんの異なるアルゴリズムが何か優先探索という一般的なアルゴリズムの変種だったことに似ています。

一般的な最小全域木アルゴリズムは入力グラフ \(G\) の非巡回部分グラフ \(F\) を管理します。\(F\) は中間全域森 (intermediate spanning forest) と呼ばれ、アルゴリズムの各時点において次の不変条件を満たします:

\(F\) は \(G\) の最小全域木の部分グラフである。

一般的な最小全域木アルゴリズムは \(G\) の頂点一つずつからなる森を \(F\) とした状態から始まり、各反復で頂点の間に辺を加えて木をつなげていきます。アルゴリズムが停止したとき \(F\) は一つの全域木となり、不変条件からそれが \(G\) の最小全域木となるという寸法です。もちろん最小全域木に含まれない辺も存在するので、森に加える辺は慎重に選ばなければなりません。

森に辺を加えるとき、グラフの辺は中間全域森 \(F\) によって三つに分類されます:

全ての最小全域木アルゴリズムは二つの単純な観察に基づいています。一つ目の観察は Robert Prim (ロバート・プリム) によって 1957 年に証明されたもので (ただしそれよりも前のアルゴリズムにも暗黙の内に含まれていましたが)、二つ目の観察はほとんど自明です。

命題 7.2 (Prim). \(G\) の最小全域木は全ての安全な辺を含む。

証明 「\(G\) の頂点の任意の部分集合 \(S\) について、\(G\) の最小全域木には端点のちょうど一方が \(S\) に含まれる辺のうち重みが最小のものが含まれる」というより強い命題を示す: 命題 7.1と同じように、貪欲な交換の議論を使ってこの命題を示す。

\(S\) を \(G\) の頂点の任意の部分集合とし、\(e\) を端点のちょうど一方が \(S\) に含まれる \(G\) の辺のうち重みが最小なものとする (辺の重みが全て異なると仮定しているので、\(e\) は曖昧さなく選べる)。\(T\) を \(e\) を含まない任意の \(G\) の全域木とする。これから \(T\) が \(G\) の最小全域木でないことを示す。

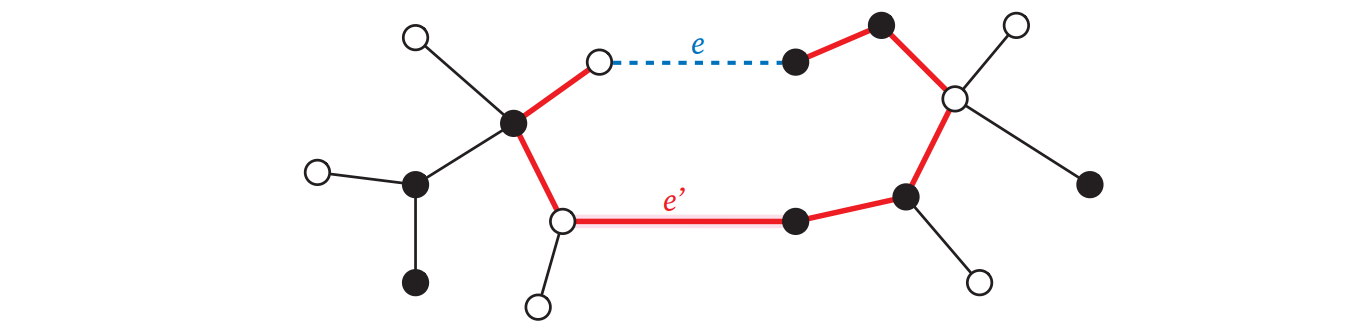
\(T\) は連結だから、\(e\) の端点同士を結ぶ路が存在する。この路は \(S\) に含まれる頂点と \(S\) に含まれない頂点を結んでいることから、この路には端点のちょうど一方が \(S\) に含まれる辺が存在する。そのような辺を適当に選んで \(e^{\prime}\) とする。\(T\) は非巡回だから、\(T\) から \(e^{\prime}\) を取り除くと二つの成分を持つ全域森となり、二つの成分は \(e\) の端点を片方ずつ含む。したがってこの森に \(e\) を加えて得られる \(T^{\prime} = T - e^{\prime} + e\) は \(G\) の全域木である。\(e\) の定義から \(w(e^{\prime}) > w(e)\) なので、\(T^{\prime}\) の重みの和は \(T\) よりも小さい。よって \(T\) は \(G\) の最小全域木ではない。 \(\Box\)

全ての安全な辺は最小全域木に含まれる (黒い頂点が部分集合 \(S\) を表す)
図 7.2
全ての安全な辺は最小全域木に含まれる (黒い頂点が部分集合 \(S\) を表す)

命題 7.3 最小全域木は不要な辺を持たない。

証明 \(F\) に不要な辺を加えると閉路ができてしまう。 \(\Box\)

一般的な最小全域木アルゴリズムを一言で言えば「\(F\) に安全な辺を繰り返し加える」です。\(G\) が連結なことから \(F\) が連結でないときには安全な辺が少なくとも一つ存在するので、どのような順番で辺を加えていったとしても \(F\) は最終的に連結となります。よって命題 7.2 から帰納法によって、最終的に出来上がる \(F\) が \(G\) の最小全域木であることが分かります。\(F\) に辺を加えると不定だった辺のいくつかが安全になったり不要になったりする (辺が不要になった場合、その辺はそれ以降ずっと不要です) ので、具体的なアルゴリズムを得るには、各反復でどの安全な辺を加えるのか、そしてどうやって安全な辺を見つけるのかを説明する必要があります。

広告
このページの文章はテキストゆれないくんを使って校正されました。