動的計画法
Potes enim videre in hac margine, qualiter hoc operati fuimus, scilicet quod iunximus primum numerum cum secundo, videlicet 1 cum 2; et secundum cum tercio; et tercium cum quarto; et quartum cum quinto, et sic deinceps....
[これまでの処理をここに示す。最初の数 \(1\) と二番目の数 \(2\) を足し、二番目と三番目を足し、三番目と四番目を足し、四番目と五番目を足し、以下同様に続く...]
過去を記憶しないものは過去を繰り返すよう運命付けられている。
学習とは何か分かっているか?
学習とは、「今何をしたか分かっているか? 二度とするな」と教えてくれるものだ。
Mātrāvṛtta
人類が再帰処理を使った一番古い例は、2000 年以上前のインドにおける詩の歩格と韻律に関する研究に見ることができます。古典サンスクリット語の詩では、音節 (akṣara) を軽い (laghu) 音節と重い (guru) 音節の二つに区別していました。mātrāvṛtta (マトラブラッタ)、 mātrāchandas (マトラチャンダス) などと呼ばれる歩格の詩では各行が同じ数の拍 (mātrā) を持ち、軽い音節は一拍、重い音節は二拍の長さを持ちます。
mātrā-vṛtta に関するきちんとした研究をさかのぼると、紀元前 600 年から 200 年の間に韻律学者 Piṅgala (ピンガラ) によって書かれた Chandaḥśāstra (チャンダシャーストラ) という文献にたどり着きます。その文献で Piṅgala は、四拍の歩格が \(- \hspace{4pt} -,\ \)\(- \bullet \bullet,\ \)\(\bullet - \bullet,\ \)\(\bullet \bullet -,\ \)\(\bullet \bullet \bullet\ \bullet\) の五つしかないことを記しています (ここで \(-\) は重い音節を、\(\bullet\) は軽い音節を表します1)。
与えられた拍が表現できる歩格の数を数える機械的な手続きについて Piṅgala は簡単なヒントを残しました2が、その問題がはっきりと表明されるのは約 1000 年後のことでした。紀元七世紀、インド人学者 Virahāṇka (ヴィラハーンカ) は Piṅgala の著作に対する注釈を執筆し、その中で \(n\) 拍で表現できる歩格の数が \(n-2\) 拍の歩格の数と \(n-1\) 拍の歩格の数の和であることを発見しました。現代的な表記を用いると、Virahāṇka が発見したのは \(n\) 拍の歩格の数 \(M(n)\) に関する次の再帰方程式です: \[ M(n) = M(n - 2) + M(n - 1) \] ベースケースの \(M(0) = 1\) (空の歩格が一つある) と \(M(1) = 1\) (一つの軽い音節からなる歩格が一つある) はすぐに分かります。
同じ再帰方程式は Virahāṇka から約 500 年後にヨーロッパで再発見されました。発見の場となったのは Leonardo of Pisa による 1202 年 の著作 Liber Abaci であり、これはヨーロッパ人による "algorism" に関する古い著作のうち最も影響力のあるものの一つです。エポニムに関するスティグラーの法則3に全く従って、Virahāṇka の再帰方程式を少し変更した次の式を、現代の私たちは Fibbonacci 数と呼んでいます。 \[ F_{n} = \begin{cases} 0 & \text{if } n = 0 \\ 1 & \text{if } n = 1 \\ F_{n-1} + F_{n-2} & \text{それ以外} \end{cases} \] 任意の \(n\) に対して \(M(n) = F_{n+1}\) が成り立ちます。
バックトラッキングは遅い
Fibbonacci 数の再帰的な定義から、\(F_{n}\) を計算する再帰的なアルゴリズムがすぐに分かります。疑似コードを次に示します:
procedure \(\texttt{RecFibo}\)(\(n\))
if \(n = 0\) then
return \(0\)
else if \(n = 1\) then
return \(1\)
else
return \(\texttt{RecFibo}\)(\(n-1\)) \(+\ \)\(\texttt{RecFibo}\)(\(n-2\))
残念ながら、このナイーブなアルゴリズムはひどく遅いです。このことを確認してみましょう。このアルゴリズムが行う再帰呼び出し以外の処理は、一度の比較と (無いこともある) 一度の加算です。そこで \(T(n)\) を \(\textsc{RecFibo}(n)\) を計算するときに \(\textsc{RecFibo}\) が呼び出される回数とすると、この関数は次の再帰方程式を満たします: \[ \begin{aligned} T(0) & = 1 \\ T(1) & = 1 \\ T(n) & = T(n - 1) + T(n - 2) + 1 \end{aligned} \] この方程式は Fibonacci 数の定義にそっくりです! 最初のいくつかの項を書き出すと、閉じた答え \(\pmb{T(n) = 2 F_{n+1} - 1}\) を予想でき、帰納法 (ヒント、ヒント) によって正しいことが確かめられます。よってこのアルゴリズムを使って \(F_{n}\) を計算するとおよそ \(2 F_{n}\) の時間がかかります。さらにこの本の範囲を超える手法4を使うと黄金比 (golden-ratio) と呼ばれる数 \(\phi = (\sqrt{5} + 1) / 2\) を使って \(F(n) = \Theta(\phi^{n})\) と書けることが分かるので、このアルゴリズムの実行時間は \(n\) に対して指数的です。
アルゴリズムの実行時間が指数的であることは、次のように直接確かめることもできます: \(\textsc{RecFibo}\) の再帰木を、葉が 0 か 1 で頂点が加算を表す二分木として表します。最終的な出力が \(F_{n}\) なので、\(\textsc{RecFibo}(1)\) を表す値が \(1\) の葉はちょうど \(F_{n}\) 個あります。簡単な帰納法による (ヒント、ヒント) 議論によって、\(\textsc{RecFibo}(0)\) がちょうど \(F_{n-1}\) 回呼ばれることが分かります (漸近表記を得るだけなら、\(\textsc{RecFibo}(0)\) が多くとも \(\textsc{RecFibo}(1)\) と同じ回数しか呼ばれないことを確認すれば十分です)。よって再帰木は \(F_{n} + F_{n-1} =\) \(F_{n+1} =\) \(O(F_{n})\) 個の葉を持ち、二分木全体の葉は \(2F_{n+1} - 1 =\) \(O(F_{n})\) 個と分かります。
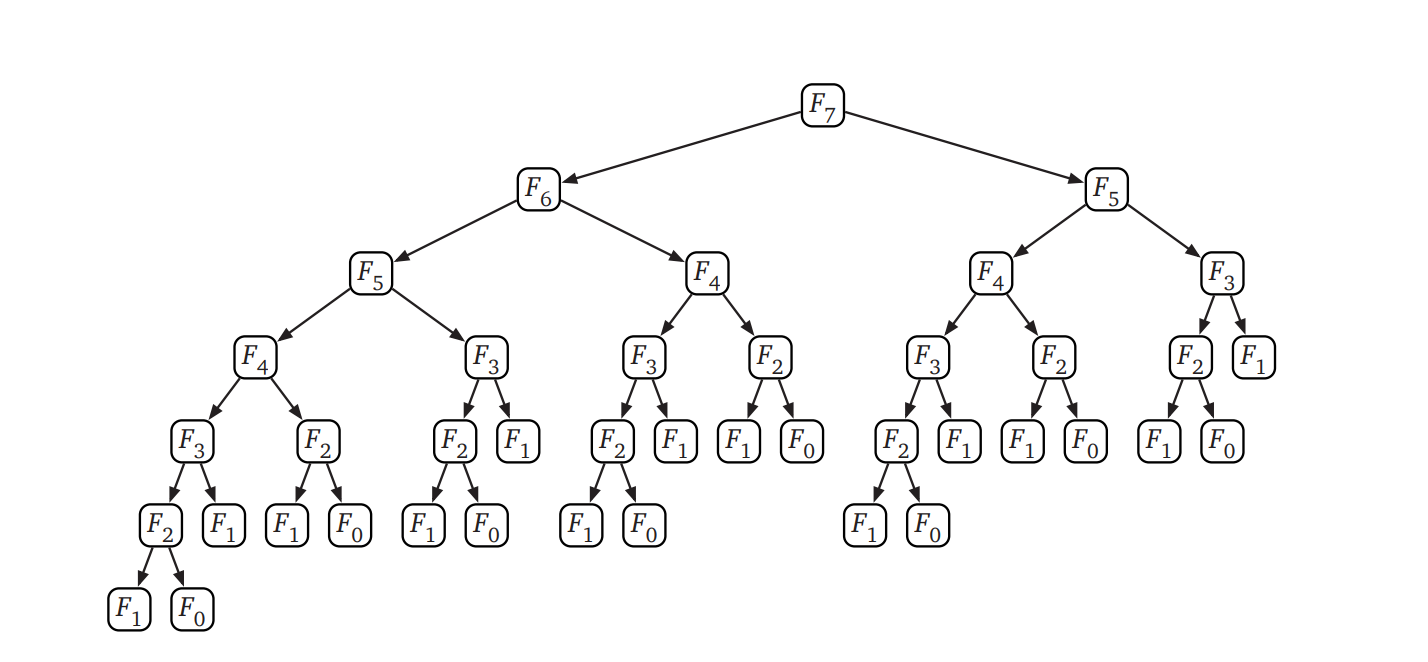
メモ化: 全てを覚える
この再帰的なアルゴリズムが遅い理由は明らかで、同じ Fibonacci 数を何度も何度も計算しているからです。\(\textsc{RecFibo}(n)\) を一度呼ぶと、再帰的な呼び出しによって \(\textsc{RecFibo}(n - 1)\) は一回、\(\textsc{RecFibo}(n - 2)\) は二回、\(\textsc{RecFibo}(n - 3)\) は三回、\(\textsc{RecFibo}(n - 4)\) は五回呼び出されます。一般的に言うと、\(0 \leq k \leq n\) について \(\textsc{RecFibo}(n - k)\) は \(F_{k-1}\) 回呼び出され、全ての呼び出しは Fibonacci 数を最初から計算します。
再帰呼び出しの結果を書き留めて後で同じ値が必要になった時にそれを参照するようにすれば、それだけでこの再帰的なアルゴリズムの実行速度を大きく向上させることができます。この最適化テクニックはメモ化 (memoization、r は付きません) と呼ばれます。メモ化は 1967 年に Donald Michie (ドナルド・ミッキー) よって提案されたとされることが多いですが、本質的に同じテクニックは 1959 年に Arthur Samuel (アーサー・サミュエル) によって提案されています5。
procedure \(\texttt{MemFibo}\)(\(n\))
if \(n = 0\) then
return \(0\)
else if \(n = 1\) then
return \(1\)
else
if \(F[n]\) が定義されていない then
\(F[n] \leftarrow\)\(\texttt{MemFibo}\)(\(n-1\)) \(+\)\(\texttt{MemFibo}\)(\(n-2\))
return \(F[n]\)
メモ化によって実行時間が小さくなるというのは明らかですが、正確にどれくらい小さくなるのでしょうか? \(\textsc{MemFibo}\) の再帰呼び出しをたどって考えると、\(F[i]\) が埋まるのは \(F[i-1]\) が埋まったときだけなことが分かります。よって帰納法から配列 \(F[]\) は \(F[2], F[3], \ldots , F[n]\) と一番下から埋まることが示せます。Fibbonacci 数 \(F_{i}\) に関する再帰方程式の評価には再帰呼び出しにかかるコストを無視すれば定数時間しかかからず、問題の設定上 \(F_{i}\) は全ての添え字 \(i\) について計算される必要があるので、\(\textsc{MemFibo}(n)\) が実行する加算の回数は \(O(n)\) 回です。つまり、ナイーブな再帰的アルゴリズムと比べて指数的な高速化です!
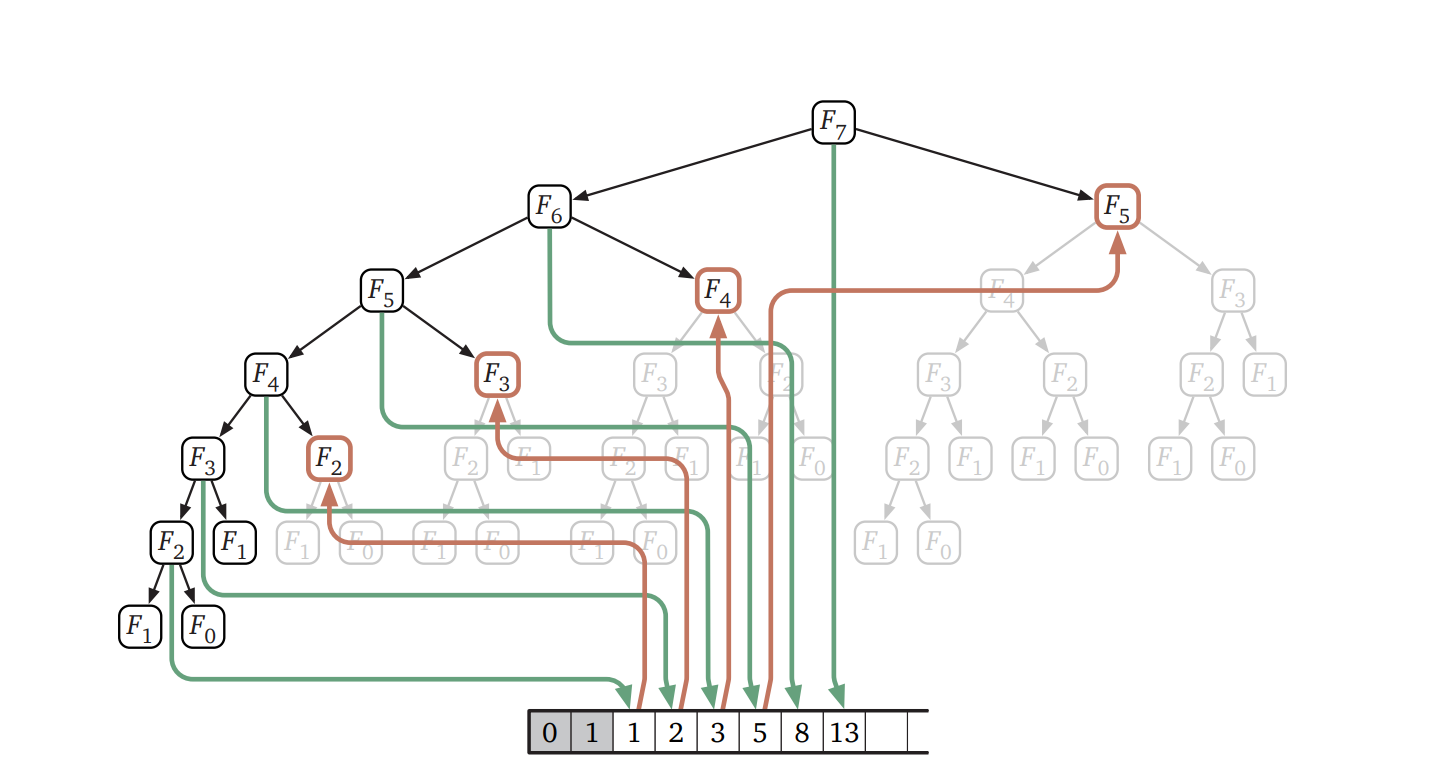
動的計画法: あらかじめ決められた順番で埋める
配列 \(F[]\) がどのように埋まるかが一度確認できてしまえば、メモ化を使う再帰的なアルゴリズムを変形して、for ループを使ってあらかじめ決められた順番で配列を埋めていくアルゴリズムを作ることができます。こうすれば、複雑な再帰呼び出しのせいで配列が埋まっていく順番が分かりにくくなっているアルゴリズム \(\textsc{MemFibo}\) を使わずにすみます。
procedure \(\texttt{IterFibo}\)(\(n\))
\(F[0] \leftarrow 0\)
\(F[1] \leftarrow 1\)
for \(i \leftarrow 2\) to \(n\) do
\(F[i] \leftarrow F[i - 1] + F[i - 2]\)
return \(F[n]\)
実行時間は瞬時に分かります: \(\textsc{IterFibo}\) は \(\pmb{O(n)}\) 回の加算を行い、\(O(n)\) 個の整数を保存します。
これがこの本で出てくる最初の動的計画法 (dynamic programming) アルゴリズムです。動的計画法というパラダイムは 1950 年代の中頃に Richard Bellman (リチャード・ベルマン) によって定式化され、広まりました。彼はそのころランド研究所に勤めていましたが、彼がこのテクニックを最初に使った人物というわけでは決してありません。例えばちょうどいま紹介した Fibonacci 数をループを使って計算するアルゴリズムは Virahāṇka とその後のサンスクリット語の韻律学者に十二世紀には知られていましたし、Fibonacci も十三世紀初頭にはこのことに気付いていました6!
Bellman はこの古くから知られていた事実に対して「動的計画法」という名前を注意深く選ぶことで、数学の研究に見えるもの全てに反対していた軍部の上司にこのアルゴリズムの数学的な要素を隠すことに成功しました7。
ここで "program" という単語はコードを書くという意味ではなく、「計画を立てる (plan)」とか「スケジュールを立てる (schedule)」に近い古い意味で使われています。計画やスケジュールを立てるときに表を埋めることが多いためにこの単語が選ばれたのでしょう。例えばスポーツや映画館の program は重要なイベント (と広告) のスケジュールを立て、テレビ番組の program は利用可能な時間の枠を番組 (と広告) で埋め、学位 program は講義 (と広告) のスケジュールを立てます。空軍が Bellman たちに予算をつけて研究させたのは、訓練と兵站のスケジュール、つまり彼らが言うところの "program" を構築する方法でした。
"dynamic" という単語が使われたのは、最適化する処理が複数のステージと時間的な広がりを持っているためというのが理由の一つです。そしておそらくは、"dynamic" という単語が、第二次世界大戦後のアメリカが持っていた「未来には何でもできるようになる」という時代精神 (Futuristic Can-Do Zeitgeist™) に共鳴するバズワードであったためでもあります8。
Bellman の布教活動のおかげもあって、動的計画法は現代の経済学、ロボット工学、制御理論などの分野における多段階計画問題に対する標準的なツールとなりました。
全て覚え無くてもよい
動的計画法を使う問題の中には、計算の中間結果の全てを最後まで記憶しておく必要がないものも多くあります。例えば \(\textsc{IterFibo}\) では、配列の直近二つの要素だけを覚えておくようにすることで、空間消費量を大きく削減できます:
procedure \(\texttt{IterFibo2}\)(\(n\))
\(\mathit{prev} \leftarrow 1\)
\(\mathit{curr} \leftarrow 0\)
for \(i \leftarrow 0\) to \(n\) do
\(\mathit{next} \leftarrow \mathit{curr} + \mathit{prev}\)
\(\mathit{prev} \leftarrow \mathit{curr}\)
\(\mathit{curr} \leftarrow \mathit{next}\)
return \(\mathit{curr}\)
(このアルゴリズムは \(F_{-1} = 1\) というベースケースを使っています。これは通常の定義と異なりますが、\(\textsc{IterFibo}(0)\) が \(0\) を返すので以前の定義と矛盾しません。また空間消費量の抑制は実際のプログラムでとても重要になりますが、この本では空間の問題について深く議論しません)
❤ 余談: さらに高速な Fibonacci 数
先ほど示したアルゴリズムは単純で魅力的でしたが、Fibonacci 数を計算する最速のアルゴリズムではありません。Fibbonacci 数を定義する再帰方程式を次のように行列の式として表すと、これまでより速いアルゴリズムが作れます: \[ \begin{bmatrix} 0 & 1 \\ 1 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} y \\ x + y \end{bmatrix} \] この式を言い換えると、二次元ベクトルに行列 \(\begin{bmatrix} 0 & 1 \\ 1 & 1 \end{bmatrix}\) を掛けることが \(\textsc{IterFibo2}\) の for ループを一回進めるのとちょうど同じ効果を持っているということです。よって行列を \(n\) 回掛ければ for ループを \(n\) 回反復できます: \[ \begin{bmatrix} 0 & 1 \\ 1 & 1 \end{bmatrix}^n \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} F_{n-1} \\ F_{n} \end{bmatrix} \] つまり \(n\) 個目の Fibonacci 数を計算する問題は \(\begin{bmatrix} 0 & 1 \\ 1 & 1 \end{bmatrix}\) の \(n\) 乗を計算する問題となります。二乗を反復して用いれば9、\(n\) 乗の計算には \(O(\log n)\) 回の "乗算" しか必要になりません。今の問題では "乗算" が \(2 \times 2\) の行列乗算であり、この行列乗算は定数回数の整数乗算と整数加算からなるので、\(F_{n}\) は \(\pmb{O(\log n)}\) 回の整数演算で計算できます。
行列を使わなくても、\(F_{n} =\) \(F_{m}F_{n - m - 1} + F_{m+1}F_{n-m}\) という任意の整数 \(m, n\) に対して成り立つ等式 (証明は帰納法) を利用すれば同じ性能を達成できます。この式からは次に示す隣り合う Fibonacci 数に関する相互再帰的な等式が得られます。この等式は Édouard Lucas (エドゥアール・リュカ) によって 1898 年に初めて示されました: \[ \begin{aligned} F_{2n-1} & = F_{n-1}^{2} + F_{n}^{2} \\ F_{2n} & = F_{n}(F_{n-1} + F_{n+1}) = F_{n}(2F_{n-1} + F_{n}) \end{aligned} \] (行列の二乗を使ったアルゴリズムからこの相互再帰的な方程式を得ることもできます) この式から次のアルゴリズムがすぐに得られます:
⟨⟨\(F_{n-1}, F_{n}\) の組を計算する⟩⟩
procedure \(\texttt{FastRecFibo}\)(\(n\))
if \(n = 1\) then
return \(0, 1\)
else
\(m \leftarrow \lfloor n/2 \rfloor\)
\(\mathit{hprv},\ \mathit{hcur} \leftarrow\)\(\texttt{FastRecFibo}\)(\(m\)) \(\quad \phantom{,}\) ⟨⟨\(F_{m-1},\ F_{m}\)⟩⟩
\(\mathit{prev} \leftarrow \mathit{hprv}^{2} + \mathit{hcur}^{2}\) \(\quad \hphantom{,,,,,,,,,,}\) ⟨⟨\(F_{2m-1}\)⟩⟩
\(\mathit{curr} \leftarrow \mathit{hcur} \cdot (2 \cdot \mathit{hprv} + \mathit{hcur})\) \(\quad \phantom{..}\) ⟨⟨\(F_{2m}\)⟩⟩
\(\mathit{next} \leftarrow \mathit{prev} + \mathit{curr}\) \(\quad \, \hphantom{,,,,,,,,,,,,}\) ⟨⟨\(F_{2m+1}\)⟩⟩
if \(n\) が偶数 then
return \(\mathit{prev},\ \mathit{curr}\)
else
return \(\mathit{curr},\ \mathit{next}\)
通常の再帰木の方法を使うと、このアルゴリズムが整数演算を \(O(\log n)\) 回行うことが分かります。
ループを使ったアルゴリズムは最初の再帰的なアルゴリズムを指数的に高速化したものでしたが、それをさらに指数的に高速化できました。そうですよね?
うわ! たいして速くない!
正確に言うと、実はそうではありません。Fibonacci 数は指数的に大きくなり、\(n\) 番目の Fibonacci 数は 10 進表記で \(n \log \phi \approx n / 5\) 桁、二進表記で \(n \log_{2} \phi \approx 2n/3\) 桁の数となります。このため \(F_{n}\) を対数時間で計算するのは不可能です ――答えを書くだけで \(\Omega(n)\) 時間かかるのですから!
このパラドックスを解く鍵は、任意精度の算術を定数時間で行うことはできないという事実にあります。 \(M(n)\) で \(n\) 桁の数を掛けるのにかかる時間を表すことにすると、\(\textsc{FastRecFibo}\) の実行時間は再帰方程式 \(T(n) = T(\lfloor n/2 \rfloor) + M(n)\) を満たします。再帰木を書くと \(\pmb{T(n) = O(M(n))}\) が分かります。整数乗算の (2019 年時点で) 最速の実行時間は \(O(n \log n)\) なので、この値が Fibonacci 数を計算する (2019 年時点で) 最速の実行時間となります。
それではこのアルゴリズムは for ループを使った "線形" のアルゴリズムよりも遅いのでしょうか? 答えは No です。整数の足し算も常に定数時間で行えるわけではないからです。二つの \(n\) 桁の整数の加算は \(O(n)\) 時間かかるので、for ループを使ったアルゴリズム \(\textsc{IterFibo}\) と \(\textsc{IterFibo2}\) の実行時間は \(\pmb{O(n^{2})}\) です (このことを示せますか?)。 そのため、 \(\textsc{FastRecFibo}\) は for ループを使ったアルゴリズムよりも格段に高速です。ただし指数的に高速ではありません。
最初にあげた再帰的なアルゴリズムでは、任意精度の整数演算による追加のコストは大量の再帰呼び出しに隠れます。つまり正しい再帰方程式は \(T(n) =\) \(T(n - 1) + T(n - 2) + O(n)\) ですが、答えは \(T(n) = O(\phi^{n})\) のままです。
分かち書き (Interpunctio Verborum) 再訪
次に考える動的計画法の例は、前章で触れた文字列分割の問題です。この問題の入力は文字列が (何らかの意味で) 単語かどうかを判定するサブルーチン \(\textsc{IsWord}\) と検査する文字列 \(A[1..n]\) であり、出力は \(A\) を単語列に分割できるかどうかでした。
この問題を解いたときに使ったのは接尾部分 \(A[i..n]\) が分割できる場合に限って \(\textsc{True}\) を返す関数 \(\mathit{Splittable}(i)\) であり、\(\mathit{Splittable}(1)\) を計算することで問題を解きました。この関数は次の再帰方程式を満たします: \[ \mathit{Splittable}(i) = \begin{cases} \textsc{True} & \text{if } i > n \\ \bigvee\limits_{j = i}^{n}(\mathit{IsWord} (i, j) \land \mathit{Splittable}(j + 1)) & \text{それ以外} \end{cases} \] ここで \(\mathit{IsWord}(i, j)\) は \(\mathit{IsWord}(A[i..j])\) を省略して書いたものです。この再帰方程式はバックトラッキングを使った再帰的なアルゴリズムに直接書き換えることができ、その場合 \(\mathit{IsWord}\) は最悪ケースで \(O(2^{n})\) 回呼ばれます。
しかし考えてみると、\(A[1..n]\) という決められた長さの配列に対して関数 \(\mathit{Splittable}(i)\) を呼ぶ異なる方法は \(i = 1..n+1\) の \(n+1\) 個しかなく、\(\mathit{IsWord}\) を呼ぶ異なる方法の個数は \(1 \leq i \leq j \leq n\) を満たす添え字の組 \((i, j)\) の個数なので \(O(n^{2})\) しかありません。どうして多項式個しかない物の値を求めるのに指数的な時間をかけているのでしょうか?
小問題への再帰的な呼び出しは \(1\) から \(n+1\) の整数で特定できるので、\(\mathit{Splittable}\) 関数の値は配列 \(\mathit{SplitTable}[1..n+1]\) に格納できます。小問題 \(\mathit{Splittable}(i)\) は \(j > i\) を満たす \(\mathit{Splittable}(j)\) にのみ依存するので、メモ化された再帰的なアルゴリズムは配列を最後から降順に埋めます。これと同じ順番で配列を埋めるようにすれば、次に示す動的計画法を使ったアルゴリズムとなります:
procedure \(\texttt{FastSplittable}\)(\(A[1..n]\))
\(\mathit{SplitTable}[n+1] \leftarrow \textsc{True}\)
for \(i \leftarrow n\) downto \(1\) do
\(\mathit{SplitTable}[i] \leftarrow \textsc{False}\)
for \(j \leftarrow i\) to \(n\) do
if \( \textsc{IsWord}(i, j)\) かつ \(\mathit{SplitTable}[j+1]\) then
\(\mathit{SplitTable}[i] \leftarrow \textsc{True}\)
return \(\mathit{SplitTable}[1]\)
このアルゴリズムは \(\mathit{IsWord}\) を \(O(n^{2})\) 回しか呼び出さないので、以前のバックトラッキングを使ったアルゴリズムから指数的に高速化されています。
パターン: 賢い再帰
簡潔に言ってしまえば、動的計画法とは無駄のない再帰です。
たしかに動的計画法を使ったアルゴリズムは、途中で解く小問題の答えを配列や表などのデータ構造に保存します。しかしアルゴリズムを学ぶ生徒 (そして教師と教科書) は、この表を強調しすぎるという間違いを犯しています。表なら誰でも知っていて簡単に理解できるからそうするのでしょうが、こうするとはるかに重要な (そしてはるかに難しい) 問題である、正しい再帰方程式を見つける部分が軽視されてしまいます。正しい再帰方程式をメモ化している限り表が絶対に必須というわけではありませんが、もし再帰方程式が間違っていたら、アルゴリズムは絶対に正しく動きません。
動的計画法は表を埋めることではない!
賢く再帰を行うことだ!
動的計画法を使ったアルゴリズムを開発するときは、次に示す二つの独立したステップを踏むとよいでしょう:
-
問題を再帰的に定式化する: 全体の問題に対する再帰的な定式化あるいはアルゴリズムを、より小さい小問題を使って書く。ここが難しい部分である。細かく書くと、二つの部分に分かれる:
-
仕様: 再帰的に解きたい問題を ――どうやって問題を解くかではなく、問題が何であるかを―― 正確で分かりやすい英語で表現する。この仕様が無くては、答えを判定することはどうやっても不可能である。
-
答え: 全体の問題に対する再帰的な定式化とアルゴリズムを、全く同じ問題に対するより小さいインスタンスを使って明確に示す。
-
-
再帰方程式を解く手続きをゼロから組み立てる: 再帰方程式のベースケースから始まって最終的な答えを計算するアルゴリズムを書く。途中で生じる小問題は正しい順番で解く。この段階は次の小さな、比較的機械的なステップに分けられる。
-
小問題を特定する: 最初の入力を受け取ってから、アルゴリズムはどんな再帰呼び出しを行うか? 例えば \(\textsc{RecFibo}\) が再帰的に呼ばれるとき、引数は常に \(0\) から \(n\) までの整数だった。
-
メモ化のためのデータ構造を選択する: (a) で特定した全ての小問題の答えを格納するためのデータ構造を見つける。通常は多次元の配列だが、そうでない場合もある。
-
依存を特定する: ベースケースを除けば、全ての小問題は他の小問題の答えに依存している ――具体的にどれか? データ構造の絵を描き、一般的な要素が依存している要素へ矢印を描く。そしてその絵を定式化する。
-
正しい評価順序を見つける: 全ての小問題を一列に並び替えて、任意の小問題について、それが依存している問題が前に来るようにする。ベースケースを最初に考え、次にベースケースだけに依存する問題、といった風に順番に最後の問題まで考えていくのが良い。一つ前のステップで特定した依存関係が小問題の間の半順序を定義すると考えれば、このステップで求めるのはその順序の線形拡大である。
-
消費空間および実行時間を解析する: メモ化されたアルゴリズムの消費空間量は、異なる小問題の数によって決まる。全体の実行時間を求めるには、より深い再帰呼び出しが全てメモ化されていると仮定した上での、全ての小問題の実行時間の和を求める。このステップは (a) の直後に行うことができる。
-
アルゴリズムを書く: 小問題をどの順番でどう解くかが分かったので、書く!データ構造が配列ならば、再帰方程式を何回かネストされた for ループで包み、再帰呼び出しを配列のルックアップに変えれば済むことが多い。
-
もちろん、全てのステップには正しさの証明が必要です。再帰方程式が間違っていたり、答えを間違った順序で組み立てていたりすると、アルゴリズムは正しく動きません!
警告: 貪欲は愚か
本当に運が良ければ、再帰方程式や表などを何も考えない貪欲な (greedy)アルゴリズムで問題が解けてしまうことがあります。貪欲なアルゴリズムはバックトラッキングを使ったアルゴリズムと同じように決断を積み重ねることで解を作りますが、再帰的な小問題を解くことなく愚直に一度だけ決断を行います。このアプローチはとても自然に見えるかもしれませんが、上手く行くことはまずありません。貪欲なアルゴリズムによって解ける最適化問題はとても稀です。にもかかわらず、多くの学生はバックトラッキングや動的計画法を使って解くべき問題の多くに対して貪欲な戦略を最初にひらめきます。
例えば分かち書きの問題に対する貪欲なアルゴリズムとして、入力の文字列の接頭部分の単語で最短 (あるいは最長) のものを選び、それを最初の単語と決めつけ、入力の接尾部分に対して再帰的に同じことを行う、という処理が考えられます。あるいは最長増加部分列の問題に対する貪欲なアルゴリズムとして、入力配列から一番小さな要素を出力配列の先頭として選び、それよりも後ろの部分から最長増加部分列を再帰的に選ぶ、という処理が考えられます。こういったやり方が馬鹿げたハックに思えたなら、ご名答です。これらは正しい解法からかけ離れています。
というわけで、あなたは次の文章をタトゥーにして、腕の内側、対数とビッグオー表記の公式の隣にしっかりと刻んでおくべきです:
貪欲なアルゴリズムは絶対にダメだ!
線形計画法を使え!
え、絶対に?
そうだ、絶対だ!
え、絶対に?
...まず間違いなく絶対だ10。
貪欲な解法が非常に誘惑的であるにもかかわらず正しいことがほとんど無いために、私はアルゴリズムの講義における次のポリシーを提唱しています。アルゴリズムの正しさの証明を普通は求めないような講義であっても (というより、そのような講義であればなおのこと)、このポリシーをお勧めします11。
宿題や試験において貪欲なアルゴリズムを解答した場合、たとえアルゴリズムが正くても、正しさのきちんとした証明が無いならば点数を一切与えない。
さらに言えば、生徒が貪欲なアルゴリズムを提出しがちな問題は、動的計画法を使って解くのがベストなことがほとんどです。そこで私はアルゴリズムの講義を取った生徒に対して、次のアドバイスを必ずするようにしています:
貪欲 (greeDY) という単語を書いたとき、あるいは考えたときにさえ、あなたは無意識のうちに動的計画法 (DYnamic programming) を考えている。
解こうと思えば貪欲なアルゴリズムで解くことができる問題であっても、まずはバックトラッキングや動的計画法を使ったアルゴリズムを作った方が速く作れて生産的なことが普通です。「まず動くようにせよ。それから速くせよ」です。貪欲なアルゴリズムが特定の問題の対しては正しいことを示すテクニックについては次の章で見ます。
最長増加部分列
前の章で考えた問題の中に、与えられた数値の配列 \(A[1..n]\) に含まれる一番長い増加部分列の長さを求めるという問題があり、この問題に対するバックトラッキングを使ったアルゴリズムを二つ説明しました。どちらも最悪ケースの実行時間が \(O(2^{n})\) でしたが、両方とも動的計画法を使うことで著しい高速化が可能です。
一つ目の再帰方程式: これは次?
一つ目のバックトラッキングを使ったアルゴリズムが評価するのは、全ての要素が \(A[i]\) よりも大きい \(A[j..n]\) の増加部分列で一番長いものの長さを返す関数 \(\mathit{LISBigger}(i, j)\) です。この関数に対しては次の再帰方程式が成り立っていました: \[ \mathit{LISBigger}(i, j) = \begin{cases} 0 & \text{if } j > n \\ \mathit{LISBigger}(i, j + 1) & \text{if } A[i] \geq A[j] \\ \max \left\lbrace \begin{array}{c} \mathit{LISBigger} (i, j + 1) \\ 1 + \mathit{LISBigger}(j, j + 1) \end{array} \right\rbrace & \text{それ以外} \end{cases} \] 元の問題を解くには、門番 \(A[0] = -\infty\) を入力配列に追加した上で \(\mathit{LISBigger}(0, 1)\) を計算します。
再帰的に登場する小問題は二つの添え字 \((i, j)\) で特定できます。したがって考えるべき異なる小問題は \(O(n^{2})\) 個だけであり、この小問題の結果は二次元配列 \(\mathit{LISBigger}[0..n, 1..n]\) に格納できます12。さらに、再帰呼び出しを無視した場合の小問題は \(O(1)\) 時間で解けるので、最終的に出来上がる動的計画法を使うアルゴリズムの実行時間は \(O(n^{2})\) になると予想できます。
この再帰的なアルゴリズムをメモ化を使うように書き換えたとして、そのアルゴリズムが配列を埋める順番は今までの例ほど明らかではありません。再帰方程式を見て分かるのは、\(\mathit{LISBigger}[i, j]\) が埋まるのが次の列の \(\mathit{LISBigger}[i, j + 1]\) と \(\mathit{LISBigger}[j, j + 1]\) が埋まった後だということです。次の図の左側にこれを示します。
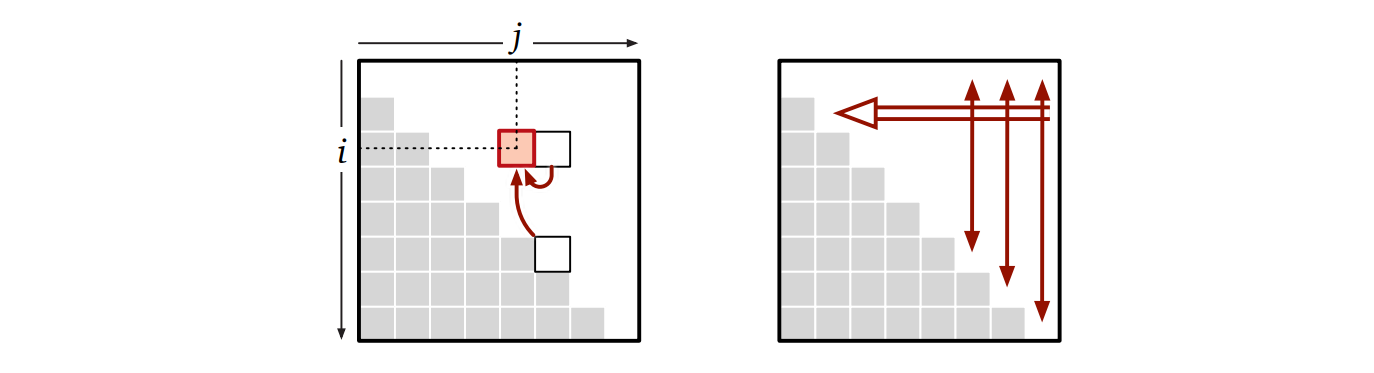
幸いにも、この部分的な情報さえあれば破綻しない評価順序を得ることができます。つまり、一列ごとに右から左へ埋めていけば、あるマスの値を埋めるときにはその値が依存している値が全て求まっているということが言えます。この順序は再帰的なアルゴリズムが表を埋めるの順序と同じではないかもしれませんが、正しく動くので、使えます。上図の右側にこの評価順序を図示します。二重の矢印が外側のループを、一重の矢印が内側のループを表します。一重の矢印が両方向を向いているのは、列の中の値を埋める順番が重要でないためです。
そして、これで終わりです! 以上の説明から得られる動的計画法を使ったアルゴリズムの疑似コードを次に示します:
procedure \(\texttt{FastLIS}\)(\(A[1..n]\))
\(A[0] \leftarrow - \infty\) \(\quad\) ⟨⟨門番を追加⟩⟩
for \(i \leftarrow 0\) to \(n\) do
⟨⟨ベースケース⟩⟩
\(\mathit{LISBigger}[i, n+1] \leftarrow 0\)
for \(j \leftarrow n\) downto \(1\) do
for \(i \leftarrow 0\) downto \(j - 1\) ⟨⟨...あるいは他の順序⟩⟩ do
\(\mathit{keep} \leftarrow 1 + \mathit{LISBigger}[j, j+1]\)
\(\mathit{skip} \leftarrow \mathit{LISBigger}[i, j+1]\)
if \(A[i] \geq A[j]\) then
\( \mathit{LISBigger}[i, j] \leftarrow \mathit{skip}\)
else
\( \mathit{LISBigger}[i,j] \leftarrow \max \lbrace \mathit{keep},\ \mathit{skip} \rbrace\)
return \(\mathit{LISBigger}[0,1]\)
このアルゴリズムが予想通り \(O(n^{2})\) 時間で実行できることはすぐに分かります。もし必要なら、使用する表の列を \(\mathit{LISBigger}[\cdot, j]\) と \(\mathit{LISBigger}[\cdot, j+1]\) という一番新しい二列だけにして、空間消費量を \(O(n^{2})\) から \(O(n)\) に落とすことができます13。
二つ目の再帰方程式: 次は何?
最長増加部分列問題を解く二つ目のバックトラッキングアルゴリズムが評価するのは、\(A[i]\) から始まる \(A[i..n]\) の増加部分列のうち一番長いものの長さを返す関数 \(\mathit{LISFirst(i)}\) です。この関数に対しては次の再帰方程式が成り立っていました: \[ \mathit{LISFirst}(i) = 1 + \max \lbrace \mathit{LISFirst}(j)\ |\ j > i \text{ かつ } A[j] > A[i] \rbrace \] ここでベースケース \(\mathit{LISFirst}(n) = 1\) が簡単に満たされるように \(\max \varnothing = 0\) と定義されます。元の問題を解くには、門番 \(A[0] = -\infty\) を入力配列に追加した上で \(\mathit{LISFirst}(0) - 1\) を計算します。
この場合では再帰的な小問題は一つの添え字 \(i\) を使って特定できるので、再帰方程式の計算結果は一次元配列 \(\mathit{LISFirst}[1..n]\) に格納できます。この配列の要素 \(\mathit{LISFirst}[i]\) は \(j > i\) を満たす \(\mathit{LISFirst}[j]\) に依存しているので、配列を降順に埋めていくことになります。 \(\mathit{LISFirst}[i]\) を計算するには \(j > i\) を満たす全ての添え字 \(j\) に対する \(\mathit{LISFirst}[j]\) が必要になりますが、\(j\) を考える順番はどんなものでも構いません。最終的に出来上がる動的計画法を使ったアルゴリズムの実行時間は \(O(n^{2})\) で、消費空間は \(O(n)\) です:
procedure \(\texttt{FastLIS2}\)(\(A[1..n]\))
⟨⟨門番を加える⟩⟩
\(A[0] = -\infty\)
for \(i \leftarrow n\) downto \(0\) do
\(\mathit{LISFirst}[i] \leftarrow 1\)
for \(j \leftarrow i + 1\) to \(n\) ⟨⟨この順番でなくても良い⟩⟩ do
if \(A[j] > A[i]\) かつ \(1 + \mathit{LISFirst}[j] > \mathit{LISFirst}[i]\) then
\( \mathit{LISFirst}[i] \leftarrow 1 + \mathit{LISFirst}[j]\)
⟨⟨門番は数えない⟩⟩
return \( \mathit{LISFirst}[0] - 1\)
編集距離
二つの文字列の間の編集距離 (edit distance)とは、一方の文字列をもう片方と同じ文字列に変形するために必要となる、文字の挿入、削除、置換の最小回数です。例えば \(\color{maroon}{\texttt{FOOD}}\) は次のように \(\color{maroon}{\texttt{MONEY}}\) に変形できるので、\(\color{maroon}{\texttt{FOOD}}\) と \(\color{maroon}{\texttt{MONEY}}\) の間の編集距離が最大でも \(4\) であることが分かります: \[ {\color{maroon}\texttt{FOOD}} \rightarrow {\color{maroon}\texttt{MOOD}} \rightarrow {\color{maroon}\texttt{MOND}} \rightarrow {\color{maroon}\texttt{MONED}} \rightarrow {\color{maroon}\texttt{MONEY}} \]
この距離関数は暗号理論を研究していた Vladimir Levenshtein (ウラジミール・レーベンシュタイン) によって 1965 年に、音声認識を研究していた Taras Vintsyuk (タラス・ヴィンチュク) によって 1968 年に、そして生物学的配列を研究していた Stanisław Ulam (スタニスワフ・ウラム) によって 1972 年に、それぞれ独立に提案されました。そのため編集距離は Levenshtein 距離あるいは Ulam 距離と呼ばれることがあります (なぜか "Vintsyuk 距離" と呼ばれることはありません)。
二つの文字列を上下に並べて書くと編集距離を可視化できます。このとき上の単語に含まれる空白は文字の挿入を、下の単語に含まれる空白は文字の削除を、上下の文字が異なる列は文字の置換を表します。このように表すと、必要となる編集の回数は同じ文字が並んでいない列の数となります: \[ \begin{aligned} \color{maroon}{\texttt{FOO D}} \\ \color{maroon}{\texttt{MONEY}} \end{aligned} \]
\(\color{maroon}{\texttt{FOOD}}\) を \(\color{maroon}{\texttt{MONEY}}\) に 3 ステップで変形させるのが不可能なのはほとんど明らかなので、\(\color{maroon}{\texttt{FOOD}}\) と \(\color{maroon}{\texttt{MONEY}}\) の間の編集距離は \(4\) となります。しかし残念ながら、一般の場合について編集の列が最短であるかどうかを判定するのはこれほど簡単ではありません。例えば次の表記からは二つの文字列 \(\color{maroon}{\texttt{ALGORITHM}}\) と \(\color{maroon}{\texttt{ALTRUISTIC}}\) の間の編集距離が最大で \(6\) なことが分かりますが、これが最小でしょうか? \[ \begin{aligned} \color{maroon}{\texttt{AL TRUISTIC}} \\ \color{maroon}{\texttt{ALGOR I THM}} \end{aligned} \]
再帰的な構造
編集距離を計算する動的計画法を使ったアルゴリズムを作るには、まず問題を再帰的に定式化する必要があります。編集距離を可視化するために文字列を上下に並べて書く今説明した表記には、「最適な小構造 (optimal substructure)」という重要な特徴があります。つまり、二つの文字列に対する最適な表記が手に入った場合、最後の列を取り除くと、残りの列が二つの接頭語に対する最小の編集回数を表すということです。この証明は簡単な帰納法です: もし二つの接頭語の間の編集距離がもっと小さかった場合、その編集の列を表す表記に取り除いた列を戻すことで、元の二つの文字列に対する編集距離よりも短い編集の列を作れますが、これは編集距離が最短の編集の列の長さであることに矛盾します。よって最後の列で何が起こるべきかが分かれば、あとは再帰の妖精が残りの最適な編集列を求めてくれます。
言い換えると、求めようとしている編集の列は右から左に並んだ編集操作によって表されます (右から左という順序に特別な意味はありません)。そして編集距離問題を解くとは、一列ごとに次の編集操作が何かを決断していくことに対応します。決断の列の途中では、二つの文字列の接尾部分が上下に並びます:

編集のコストは同じ文字が並んでいない列の数でしかないので、これからの決断にこれまでの決断が影響することはありません。これからの決断を決めるのは、まだ編集されていない接頭部分だけです。

よって \(A[1..m]\) と \(B[1..n]\) という文字列に対する編集距離問題を、次のように定式化できます: 「任意の添え字 \(i, j\) について、接頭辞 \(A[1..i]\) と \(B[1..j]\) の間の編集距離を \(\pmb{\mathit{Edit}(i, j)}\) とする。\(\mathit{Edit}(m, n)\) を求めよ」
再帰方程式
\(i, j\) を整数とします。\(A[1..i]\) と \(B[1..j]\) の最後の列に対する最適な編集を求めたい状況では、ちょうど三つの選択肢があります。
-
挿入: 最後の列の下段が空となる。このとき編集距離は \(\mathit{Edit}(i, j - 1) + 1\) である。 \(+1\) がこの挿入を表し、\(\mathit{Edit}(i, j - 1)\) が残りの部分の最適な編集回数を表す。

-
削除: 最後の列の上段が空となる。このとき編集距離は \(\mathit{Edit}(i - 1, j) + 1\) である。 \(+1\) がこの削除を表し、\(\mathit{Edit}(i - 1, j)\) が残りの部分の最適な編集回数を表す。

-
置換: どちらの段にも文字が入る。二つの文字が異なるなら編集距離は \(\mathit{Edit}(i - 1, j - 1) + 1\) である。二つの文字が同じならばこの置換は何もしないので、編集距離は \(\mathit{Edit}(i - 1, j - 1)\) である。

この解析は \(i = 0\) または \(j = 0\) のときに上手く行かなくなりますが、この場合は直接処理した方が簡単です:
-
空文字列を \(j\) 文字の文字列に変形するには \(j\) 回の挿入が必要なので、\(\mathit{Edit}(0, j) = j\)
-
\(i\) 文字の文字列を空文字列に変形するには \(i\) 回の削除が必要なので、\(\mathit{Edit}(i, 0) = i\)
検算として、二つのベースケースが両方とも空文字列同士の編集距離を正しく \(0\) と計算することを確認しておきましょう!
以上の解析から、\(\mathit{Edit}\) 関数が次の再帰方程式を満たすと言えます: \[ \mathit{Edit}(i, j) = \begin{cases} i & \text{if } j = 0 \\ j & \text{if } i = 0 \\ \min \left\lbrace \begin{array}{c} \mathit{Edit}(i, j - 1) + 1 \\ \mathit{Edit}(i - 1, j) + 1 \\ \mathit{Edit}(i - 1, j - 1) + [A[i] \neq B[j]] \end{array} \right\rbrace & \text{それ以外} \end{cases} \]
動的計画法
再帰方程式ができたので、これから動的計画法を使ったアルゴリズムを作ります。おなじみの機械的なステップを踏みます。
-
小問題: 再帰的に解く小問題は二つの添え字 \(0 \leq i \leq m\) と \(0 \leq j \leq n\) で特定できる。
-
メモ化のためのデータ構造: よって \(\mathit{Edit}(i, j)\) が取りうる全ての値は二次元配列 \(\mathit{Edit}[0..m, 0..n]\) に格納できる。
-
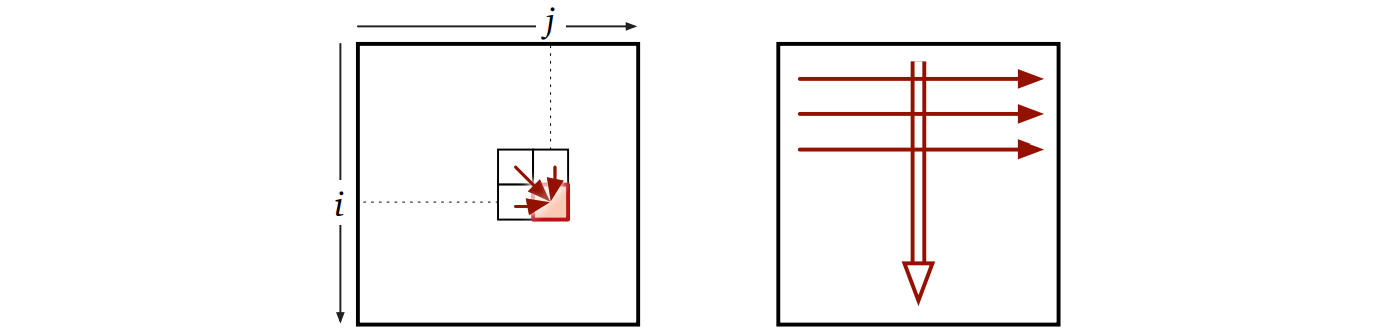
依存関係: \(\mathit{Edit}[i ,j]\) は隣り合った三つの要素 \(\mathit{Edit}[i - 1, j],\) \(\mathit{Edit}[i, j - 1],\) \(\mathit{Edit}[i - 1, j - 1]\) にのみ依存する。
-
評価順序: 配列を普通の列優先 (行は上から下、列は左から右) の順序で埋めていけば、各要素が依存する全ての値がその要素を計算するときまでに埋まる (条件を満たす評価順序はこれだけではないが、正しく動くので、これを使う)。
-
時間と空間: メモ化のためのデータ構造は空間を \(O(mn)\) だけ使う。 \(\mathit{Edit}[i, j]\) の計算はそれまでのメモが埋まっていれば \(O(1)\) でできるので、アルゴリズム全体の実行時間は \(\pmb{O(mn)}\) となる。
完成したアルゴリズムを次に示します:
procedure \(\texttt{EditDistance}\)(\(A[1..m], B[1..n]\))
for \(j \leftarrow 0\) to \(n\) do
\(\mathit{Edit}[0, j] \leftarrow j\)
for \(i \leftarrow 1\) to \(m\) do
\(\mathit{Edit}[i,0] \leftarrow i\)
for \(j \leftarrow 1\) to \(n\) do
\(\mathit{ins} \leftarrow \mathit{Edit}[i, j-1] + 1\)
\(\mathit{del} \leftarrow \mathit{Edit}[i-1, j] + 1\)
if \(A[i] = B[j]\) then
\(\mathit{rep} \leftarrow \mathit{Edit}[i-1, j-1]\)
else
\(\mathit{rep} \leftarrow \mathit{Edit}[i-1,j-1] + 1\)
\(\mathit{Edit}[i, j] \leftarrow \min \lbrace \mathit{ins},\ \mathit{del},\ \mathit{rep} \rbrace\)
return \(\mathit{Edit}[m, n]\)
このアルゴリズムは Robert Wagner (ロバート・ワグナー) と Michael Fischer (マイケル・フィッシャー) によって 1974 年に提案され、彼らのものとされることが最も多いです。しかしここでもエポニムに関するスティグラーの法則は働いていて、これと同じあるいはもっと一般的なアルゴリズムが 1968 年には Taras Vintsyuk によって、1970 年には N. G. Zagoruyko (G・G・ザゴルイコ) によって、 1972 年には David Sankoff (デイビット・サンコフ) によって、1974 年には Peter Sellers (ピーター・セラーズ) によってそれぞれ独立に発見され、他にも独立に発見したと思われる人物が何人かいます14。興味深いことに、ここにあげた研究者は誰一人として Levenshtein と Ulam に触れていません!
\(\color{maroon}{\texttt{ALGORITHM}}\) と \(\color{maroon}{\texttt{ALTRUISTIC}}\) に対してこのアルゴリズムを実行したときに出来上がるメモの表を次に示します。太字で書かれている部分は、注目している二つの文字が同じであることを表します。\(\color{maroon}{\texttt{ALGORITHM}}\) と \(\color{maroon}{\texttt{ALTRUISTIC}}\) の編集距離は本当に \(6\) でした!
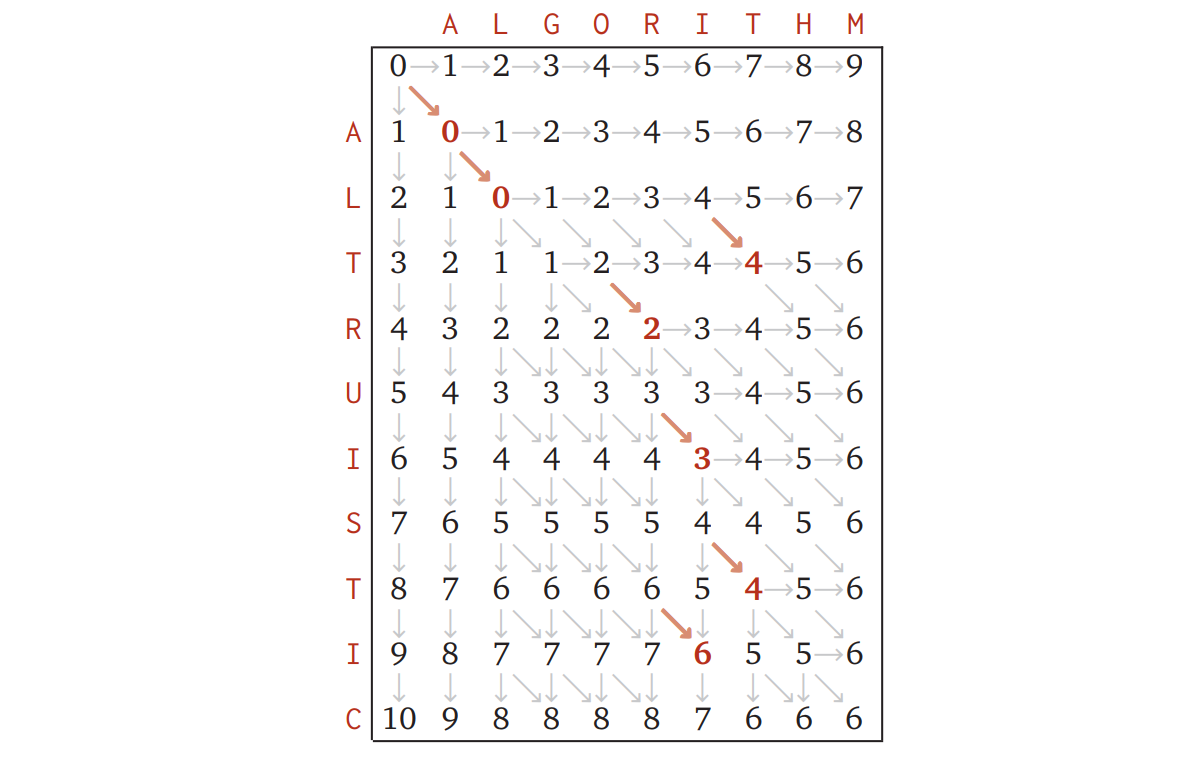
表の矢印を見れば各要素の一つ前の要素がどれかが分かるようになっており、矢印の向きは編集操作 (水平=削除, 垂直=挿入, 斜め=置換) を表します。赤くて太い斜めの矢印は二つの文字が同じであることで起こる "無料の" 置換であり、左上から右下への任意のパスが二つの文字列の間の最適な編集操作の列を表します。この例では左上から右下へのパスは三つあり、それぞれ以下の表記に対応します: \[ \begin{gathered} \color{maroon}{\texttt{ALTRUISTIC }} \\ \color{maroon}{\texttt{ALGORI THM }} \end{gathered} \] \[ \begin{gathered} \color{maroon}{\texttt{AL TRUISTIC}} \\ \color{maroon}{\texttt{ALGOR I THM}} \end{gathered} \] \[ \begin{gathered} \color{maroon}{\texttt{ALT RUISTIC}} \\ \color{maroon}{\texttt{ALGOR I THM}} \end{gathered} \]
\(\textsc{EditDistance}\) アルゴリズムはこの矢印の方向を計算したり表に保存したりしませんが、表の値が求まっていれば一つの矢印は \(O(1)\) 時間で計算できます。したがって表が全て埋まっていれば、最短の編集列は \(O(m+n)\) 時間を追加することで計算できます。
部分和問題
前章で触れた部分和問題とは、正の整数の配列 \(X[1..n]\) と整数 \(T\) を受け取って \(X\) の部分集合で和が \(T\) となるものがあるかどうかを答える問題です。前章ではこの問題に対する再帰的なアルゴリズムを次の真偽値関数 \(SS(i,t)\) を使って定式化しました。この式では入力 \(X[1..n]\) と \(T\) が固定されています: \[ SS(i, t) = \textsc{True} \Leftrightarrow X[i..n] \text{ の部分集合で和が }t \text{ になるものが存在する} \] 計算すべきは \(SS(1,T)\) です。この関数は次の再帰方程式を満たしました: \[ SS(i, t) = \begin{cases} \textsc{True} & \text{if } t = 0 \\ \textsc{False} & \text{if } t < 0 \text{ or } i > n \\ SS(i + 1, t) \lor SS(i + 1, t - X[i]) & \text{それ以外} \end{cases} \]
おなじみのボイラープレートを使えば、この再帰方程式を動的計画法のアルゴリズムに変形できます。
-
小問題: 再帰的な小問題は添え字 \(0 \leq i \leq n+1\) と整数 \(t \leq T\) で特定できる。ここで \(t < 0\) のときの答えは自明だから、メモを取らないようにする15。あるいは再帰方程式を書き換えて、\(t\) が負にならないようにすることもできる。 \[ SS(i, t) = \begin{cases} \textsc{True} & \text{if } t = 0 \\ \textsc{False} & \text{if } t < 0 \text{ or } i > n \\ SS(i + 1, t) & \text{if } t < X[i] \\ SS(i + 1, t) \lor SS(i + 1, t - X[i]) & \text{それ以外} \end{cases} \]
-
メモ化のためのデータ構造: 二次元配列 \(S[1..n+1, 0..T]\) に再帰方程式の値を格納できる。ここで \(S[i, t]\) が \(SS(i ,t)\) を表す。
-
評価順序: \(S[i,t]\) は最大で二つの要素に依存し、どちらも \(SS[i+1, \cdot]\) という形をしている。したがって、外側のループで行を下から上に、内側のループで列を適当な順番で考えていけば、詰まることなく配列を埋めることができる。
-
空間と時間: メモ化のためのデータ構造は空間を \(O(nT)\) だけ使う。\(S[i+1, t]\) と \(S[t+1, t - X[i]]\) が既知のとき \(S[i,t]\) は定数時間で計算できるので、アルゴリズム全体の実行時間は \(\pmb{O(nT)}\) となる。
完成したアルゴリズムを示します:
procedure \(\texttt{FastSubsetSum}\)(\(X[1..n], T\))
\(S[n+1, 0] \leftarrow \textsc{True}\)
for \(t \leftarrow 1\) to \(T\) do
\(S[n+1, t] \leftarrow \textsc{False}\)
for \(i \leftarrow n\) downto \(1\) do
\(S[i,0] = \textsc{True}\)
for \(t \leftarrow 1\) to \(X[i] - 1\) do
⟨⟨\(t < 0\) を除外する⟩⟩
\(S[i,t] \leftarrow S[i+1, t]\)
for \(t \leftarrow X[i]\) to \(T\) do
\(S[i, t] \leftarrow S[i+1,t] \lor S[i+1, t-X[i]]\)
return \(S[1,T]\)
バックトラッキングを使った再帰的なアルゴリズムの実行時間は \(O(2^{n})\) だったので、最悪計算時間が \(O(nT)\) というのは \(T\) が小さい場合には非常に大きな高速化です16。しかしもし目標の値 \(T\) が \(2^{n}\) よりもはるかに大きい場合、この for ループを使ったアルゴリズムは再帰的なアルゴリズムが考えない小問題を考えることになり、ナイーブな再帰的アルゴリズムよりも遅くなります。動的計画法は常に実行時間を改善するわけではありません17!
最適二分探索木
前章で最後に考えたのは最適二分探索木の問題でした。入力は探索のためのソートされた鍵 \(A[1..n]\) と頻度 \(f[1..n]\) であり、\(f[i]\) が \(A[i]\) に対する探索の回数を表します。出力は入力の鍵に対する二分探索木であって全ての探索の合計時間を最小にするものです。
頻度を表す配列 \(f\) を固定し、\(A[i..k]\) の最適探索時間を \(\mathit{OptCost}(i,k)\) とすると、次の再帰方程式が成り立つことを前章で見ました: \[ \mathit{OptCost}(i, k) = \begin{cases} 0 & \text{if } i > k \\ \displaystyle \sum_{j=i}^{k}f[j] + \min\limits_{i \leq r \leq k} \left \lbrace \begin{array}{l} \mathit{OptCost}(i, r-1) \\ \ + \mathit{OptCost}(r+1, k) \end{array} \right \rbrace & \text{それ以外} \end{cases} \] これから何をするのか想像がつくと思いますが、まずは和をどうにかします。
添え字の組 \(i,k\) (\(i \leq k\)) に対して、 鍵 \(A[i..k]\) に対応する頻度の合計を \(F(i, k)\) で表すことにします: \[ F(i, k) := \sum_{j=i}^{k}f[j] \] この関数は次の単純な再帰方程式を満たします: \[ F(i, k) := \begin{cases} f[i] & \text{if } i = k \\ F(i, k - 1) + f[k] & \text{それ以外} \end{cases} \] \(F(i, k)\) がとりうる全ての値は \(O(n^{2})\) 時間で計算できます。計算には、もちろん、動的計画法を使います。何度も使ってきた機械的なステップを踏めば、次のアルゴリズムとなります:
procedure \(\texttt{InitF}\)(\(f[1..n]\))
for \(i \leftarrow 1\) to \(n\) do
\(F[i,i-1] \leftarrow 0\)
for \(k \leftarrow i\) to \(n\) do
\(F[i,k] \leftarrow F[i, k - 1] + f[k]\)
このアルゴリズムは初期化処理として利用します。\(F\) を初期化しておけば、再帰方程式を次のように単純化できます: \[ \mathit{OptCost}(i, k) = \begin{cases} 0 & \text{if } i > k \\ \displaystyle F[i, k] + \min\limits_{i \leq r \leq k} \left \lbrace \begin{array}{l} \mathit{OptCost}(i, r-1) \\ \ + \mathit{OptCost}(r+1, k) \end{array} \right \rbrace & \text{それ以外} \end{cases} \] さあ、準備は整いました。
-
小問題: 再帰的な小問題は二つの整数 \(i, k\) (\(1 \leq i \leq n + 1\), \(0 \leq k \leq n\)) で特定できる。
-
メモ化: \(\mathit{OptCost}\) が取り得る値は二次元配列 \(\mathit{OptCost}[1..n+1, 0..n]\) に格納できる (実際に使われるのは \(j \geq i - 1\) を満たす \(\mathit{OptCost}[i,j]\) だけだが、気にしない)。
-
依存関係: \(\mathit{OptCost}[i, k]\) は全ての \(i\leq j \leq k\) について \(\mathit{OptCost}[i, j-1]\) と \(\mathit{OptCost}[j+1, k]\) に依存している。言い換えれば、表の任意の要素は下と左にある全ての要素に依存している:
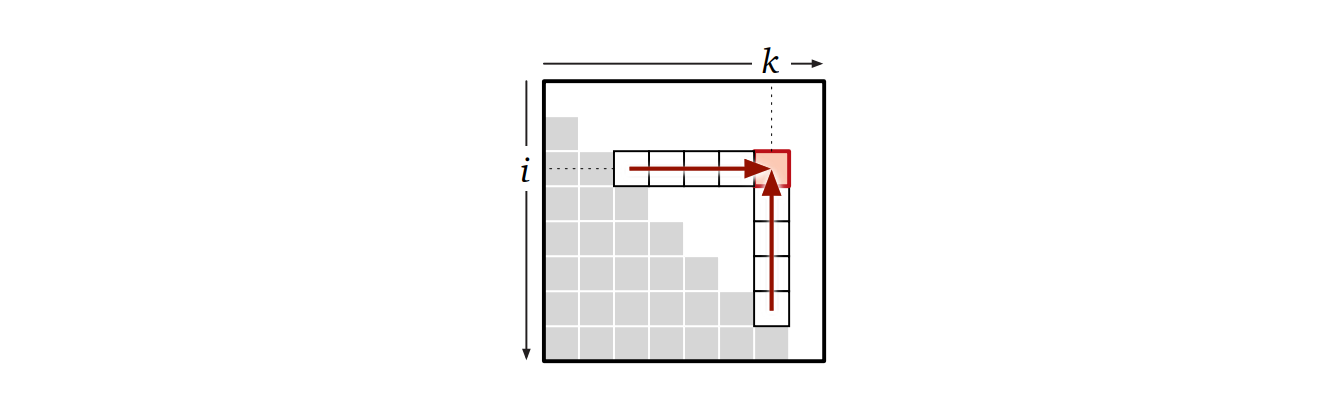
依存する全ての値が計算されていると仮定すれば、\(\mathit{OptCost}[i,k]\) は次のサブルーチンで計算できる:
procedure \(\texttt{ComputeOptCost}\)(\(i,k\))
\(\mathit{OptCost}[i,k] \leftarrow \infty\)
for \(r \leftarrow i\) to \(k\) do
\(\mathit{tmp} \leftarrow \mathit{OptCost}[i, r-1] + \mathit{OptCost}[r+1,k]\)
if \(\mathit{OptCost}[i,k] > \mathit{tmp}\) then
\(\mathit{OptCost}[i,k] \leftarrow \mathit{tmp}\)
\(\mathit{OptCost}[i,k] \leftarrow \mathit{OptCost}[i,k] + F[i,k]\)
-
評価順序: 配列を埋めるのに使える順序は少なくとも三つはある。多くの生徒が最初に思いつくのは、ベースケース \(\mathit{OptCost}[i, i-1]\) から初めて対角線ごとに \(\mathit{OptCost}[1,n]\) に向かって埋めていくというものである:
procedure \(\texttt{OptimalBST}\)(\(f[1..n]\))
\(\texttt{InitF}\)(\(f(1..n)\))
for \(i \leftarrow 1\) to \(n+1\) do
\(\mathit{OptCost}[i,i-1] \leftarrow 0\)
for \(d \leftarrow 0\) to \(n-1\) do
for \(i \leftarrow 1\) to \(n - d\) ⟨⟨他の順序でもよい⟩⟩ do
\(\texttt{ComputeOptCost}\)(\(i, i+d\))
return \(\mathit{OptCost}[i,n]\)
行優先で行を左からに右、列を下から上という順序、あるいは列優先で列を下から上、行を左から下という順序でも配列を埋めることができる:
procedure \(\texttt{OptimalBST2}\)(\(f[1..n]\))
\(\texttt{InitF}\)(\(f(1..n)\))
for \(i \leftarrow n+1\) downto \(1\) do
\(\mathit{OptCost}[i,i-1] \leftarrow 0\)
for \(j \leftarrow i\) to \(n\) do
\(\texttt{ComputeOptCost}\)(\(i, j\))
return \(\mathit{OptCost}[i,n]\)
procedure \(\texttt{OptimalBST3}\)(\(f[1..n]\))
\(\texttt{InitF}\)(\(f(1..n)\))
for \(j \leftarrow 0\) to \(n+1\) do
\(\mathit{OptCost}[i,i-1] \leftarrow 0\)
for \(i \leftarrow j\) downto \(1\) do
\(\texttt{ComputeOptCost}\)(\(i, j\))
return \(\mathit{OptCost}[i,n]\)
三つの評価順序を図示すると以下のようになる。二重の矢印が外側のループを表し、一重の矢印が内側のループを表す。両方向の矢印はそのループの評価順序がどんなものでも構わないことを示す。
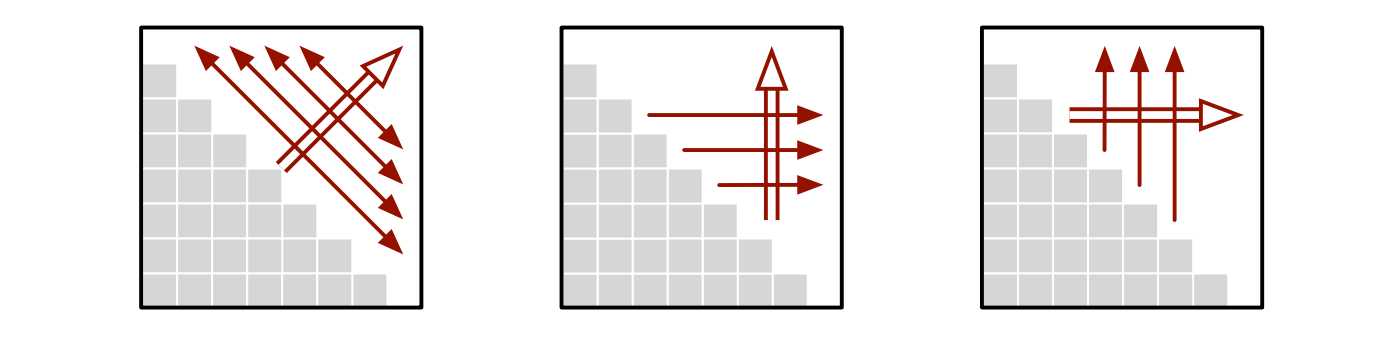
-
時間と空間 メモ化のためのデータ構造は空間を \(O(n^{2})\) だけ使う。どの評価順序を選んだとしても \(\mathit{OptCost}[i,k]\) の計算には \(O(n)\) 時間が必要なので、アルゴリズム全体の実行時間は \(\pmb{O(n^{3})}\) となる。
これまでの動的計画法を使ったアルゴリズムと同じように、消費空間と実行時間の上限は元の再帰方程式から見積ることもできます: \[ \mathit{OptCost}(i, k) = \begin{cases} 0 & \text{if } i > k \\ \displaystyle F[i, k] + \min\limits_{i \leq r \leq k} \left \lbrace \begin{array}{l} \mathit{OptCost}(i, r-1) \\ \ + \mathit{OptCost}(r+1, k) \end{array} \right \rbrace & \text{それ以外} \end{cases} \] \(\mathit{OptCost}\) 関数は二つの引数を取り、そのどちらもおおよそ \(n\) 個の異なる値を取るので、サイズが \(O(n^{2})\) のデータ構造が必要になると予想できます。また再帰方程式の本質的な部分には三つの変数 (\(i,k,r\)) があり、それぞれがおおよそ \(n\) 個の異なる値を取るので、全ての値を計算するには \(O(n^{3})\) の時間がかかると予想できます。
木の上の動的計画法
今まで見てきた動的計画法の例はどれも、再帰的な小問題の答えを格納するのに多次元配列を使っていました。しかし次の例が示すように、配列が常に一番良いデータ構造であるとは限りません。
グラフの独立集合 (independent set) とは、頂点の部分集合であってどの頂点の間にも辺がないものを言います。任意のグラフの最大独立集合を見つけるのは極端に難しい問題であり、実際これは十二章で扱う NP 困難な問題の中でも有名なものです。しかしグラフがある特別なクラスに属している場合には、最大独立集合を高速に求めることができます。例えばグラフが \(n\) 個の頂点からなる木ならば、最大独立集合は次に説明する方法を使って \(O(n)\) 時間で求められます。
木 \(T\) が与えられたとします。このとき、一般性を失うことなく \(T\) が根付きの木である、つまり根と呼ばれる頂点があり、全ての辺が暗黙のうちに根から遠ざかる方向に方向付けされていると仮定できます (もし \(T\) が根無し木 ――連結非巡回無向グラフ―― ならば、任意の頂点を根とみなすことができます)。頂点 \(w\) から根への唯一の道に頂点 \(v\) が含まれるとき、\(w\) は \(v\) の子孫 (descendant) であると言います。同様に \(v\) の子孫 (descendants) とは \(v\) および \(v\) の子の子孫を合わせたものです。また \(T\) の頂点 \(v\) を根とする部分木とは、\(v\) の子孫とそれらを結ぶ辺からなる木です。
\(T\) の任意の頂点 \(v\) に対して、\(v\) を根とする部分木の最大独立集合を \(\mathit{MIS}(v)\) と書くことにします。 \(v\) を根とする部分木の独立集合で \(v\) を含まないものは、\(v\) の子を根とする部分木の独立集合の和集合です。また \(v\) を根とする部分木の独立集合で \(v\) を含むものには \(v\) の子が含まれず、\(v\) の孫を根とする部分木の独立集合の和集合に \(v\) を加えたものとなります。以上の観察から、\(\mathit{MIS}\) は次の再帰方程式に従います。ここで \(w \downarrow v\) という標準的でない記法は「\(w\) は \(v\) の子である」を意味します。 \[ \mathit{MIS}(v) = \max \left\lbrace \sum_{w \downarrow v} \mathit{MIS}(w), 1 + \sum_{w \downarrow v} \sum_{x \downarrow w} \mathit{MIS}(x) \right\rbrace \]
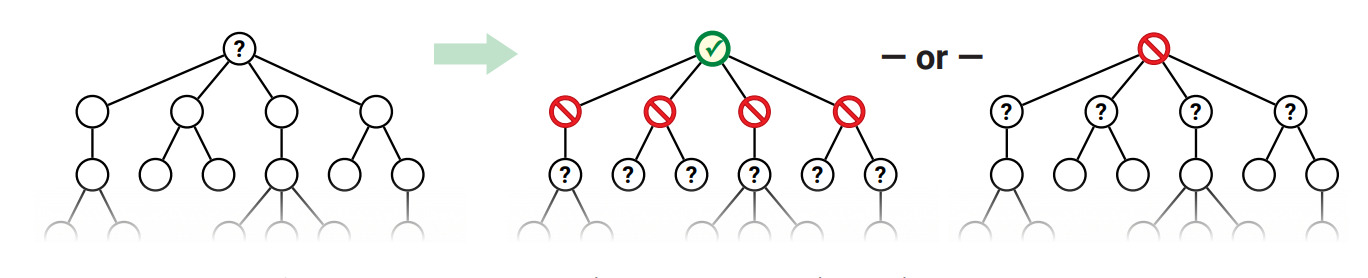
与えられた木 \(T\) の根 \(r\) について \(\mathit{MIS}(r)\) を計算することが目標となります。
この種類の再帰方程式をメモ化するときにはどのようなデータ構造を使うべきでしょうか? 自然な選択肢は木 \(\pmb{T}\) そのものです! つまり \(T\) の各頂点 \(v\) に対して、新しいフィールド \(v.\mathit{MIS}\) に \(\mathit{MIS}(v)\) を格納していくということです (理論上は木ではなく配列を使うこともできますが、頂点とそれに対応する配列の要素の間を行ったり来たりする必要があります。そんなことをする必要はないでしょう)。
小問題はどのような順番で考えればよいでしょうか? 任意の頂点 \(v\) が依存する小問題は \(v\) の子と孫の小問題なので、全ての頂点がその親よりも前にくるのであればどんな順番でも使うことができます。ここではよく知られた帰りがけ順の走査を使います。
このアルゴリズムの実行時間はどれくらいでしょうか? 頂点 \(v\) に対する小問題の再帰的でない部分の実行時間は \(v\) の子と孫の数に比例し、この数は頂点によって大きく変動するので評価が困難です。しかし、逆方向に考えると上手く行きます: 全ての頂点はその親と祖父母の小問題に対して実行時間を定数時間だけ上乗せします! 各頂点の親と祖父母は多くても一つずつなので、アルゴリズム全体は \(\pmb{O(n)}\) 時間で実行されます。
完成したアルゴリズムを次に示します。このアルゴリズムは再帰的ですが、それは木に対する帰りがけ順の走査を実装するのに再帰を使っているからであって、動的計画法を使っていないからではありません。
procedure \(\texttt{TreeMIS}\)(\(v\))
\(\mathit{skipv} \leftarrow 0\)
for \(v\) の子 \(w\) do
\(\mathit{skipv} \leftarrow \mathit{skipv} + {}\)\(\texttt{TreeMIS}\)(\(w\))
\(\mathit{keepv} \leftarrow 1\)
for \(v\) の孫 \(x\) do
\(\mathit{keepv} \leftarrow \mathit{keepv} + x.\mathit{MIS}\)
\(v.\mathit{MIS} \leftarrow \max\lbrace \mathit{keepv},\ \mathit{skipv} \rbrace\)
return \(v.\mathit{MIS}\)
\(T\) の頂点 \(v\) に対する二つの関数を次のように定義すると、さらに単純な線形時間アルゴリズムが得られます。
- \(\mathit{\mathit{MISyes}}(v)\) を、\(v\) を根とする部分木の \(v\) を含む独立集合の最大サイズとする。
- \(\mathit{\mathit{MISno}}(v)\) を、\(v\) を根とする部分木の \(v\) を含まない独立集合の最大サイズとする。
ここで計算すべきは \(T\) の根 \(r\) に対する \(\max\lbrace \mathit{\mathit{MISyes}}(r), \mathit{\mathit{MISno}}(r) \rbrace\) の値です。二つの関数は次の相互再帰方程式を満たします: \[ \begin{aligned} \mathit{\mathit{MISyes}}(v) & = 1 + \sum_{w \downarrow v} \mathit{\mathit{MISno}}(w) \\ \mathit{\mathit{MISno}}(v) & = \sum_{w \downarrow v} \max\lbrace \mathit{\mathit{MISyes}}(w), \mathit{\mathit{MISno}}(w) \rbrace \end{aligned} \] ここでも、関数の値を \(T\) と同じ形の木に格納します。関数が二つあるので、各頂点に作成される新しいフィールドは二つです。木に対する帰りがけ順の走査を使えば、全ての頂点に対する二つの関数の値を \(\pmb{O(n)}\) 時間で計算できます。次に示すアルゴリズムは \(v\) における二つの関数の値を記録するだけではなく、その二つのうちで大きい方を返します。
procedure \(\texttt{TreeMIS2}\)(\(v\))
\(\mathit{v.\mathit{MISno}} \leftarrow 0\)
\(\mathit{v.\mathit{MISyes}} \leftarrow 1\)
for \(v\) の子 \(w\) do
\(\mathit{v.\mathit{MISno}} \leftarrow \mathit{v.\mathit{MISno}} + {}\)\(\texttt{TreeMIS2}\)(\(w\))
\(\mathit{v.\mathit{MISyes}} \leftarrow \mathit{v.\mathit{MISyes}} + \mathit{w.\mathit{MISno}}\)
return \(\max \lbrace \mathit{v.\mathit{MISyes}},\ \mathit{v.\mathit{MISno}} \rbrace\)
ループの二行目の \(\mathit{w.\mathit{MISno}}\) は一つ前の行の \(MIS(w)\) の呼び出しの中で記録された値です。
練習問題
ここにあげられた練習問題を解くときには ――さらに言えば動的計画法を使うアルゴリズムを新しく作るときにはどんなときでも――、 以前に示したステップを踏むことを強く勧めます。特に、準備が完了するまでは表や for ループについて考え始めないでください。ここで言う準備とは、実際に解くことになる再帰的な小問題の英語で書かれた明解な仕様と、それを使った元の問題に対する完全な解のことです18。 まず動くようにせよ。それから速くせよ。
列/配列
-
あなたの前世は南極大陸植民地 Nadiria 州で働くレジ係で、一日の大半を客にお釣りを渡す仕事に費やしていました19。南極では紙がとても貴重で高価なので、レジ係がお釣りを渡すときにはなるべく少ない紙幣を使わなければならないと法律で定められていました。植民地の創立者の一人が数秘術的な嗜好を持っていたおかげで、夢ドル (dream dollar) と呼ばれる Nadira で流通する紙幣は $1, $4, $7, $13, $28, $52, $91, $365 という金額です。
-
♠ この問題に対する貪欲なアルゴリズムは、残りのお釣りの金額を超えない最大の紙幣を返していくというものです。例えば、 $122 に対して貪欲なアルゴリズムを適用すると、$91, $28, $1 とお釣りを渡すことになります。この貪欲なアルゴリズムを使うと理想的な枚数よりも多くの夢ドル紙幣を渡してしまう例を示してください。 [ヒント: 手で解くよりもプログラムを書いた方が早いかもしれません。]
-
整数 \(k\) が与えられたときに、\(k\) 夢ドルのお釣りを返すのに必要となる最小の紙幣の枚数を返す再帰的なアルゴリズムを説明してください (アルゴリズムの実行速度は気にしないでください: まずは正しくしてください)。
-
整数 \(k\) が与えられたときに、\(k\) 夢ドルのお釣りを返すのに必要となる最小の紙幣の枚数を返す動的計画法のアルゴリズムを説明してください (ここでは、アルゴリズムが高速であることが求められます)。
-
-
次にあげる文字列分割問題の変種を解く効率の良いアルゴリズムを説明してください。文字列を受けとってそれが "単語" である場合に限って \(\textsc{True}\) を返すサブルーチン \(\textsc{IsWord}\) が使えると仮定し、アルゴリズムの解析では \(\textsc{IsWord}\) の呼び出し回数の上限を求めてください。
-
文字列 \(A[1..n]\) が与えられたときに、\(A\) を単語の並びに分割する方法の数を求める。例えば、\(\color{maroon}{\texttt{ARTISTOIL}}\) という文字列は \(\color{maroon}{\texttt{ARTIST} \cdot \texttt{OIL}}\) と \(\color{maroon}{\texttt{ART} \cdot \texttt{IS} \cdot \texttt{TOIL}}\) に分割できるので、アルゴリズムはこの文字列に対して \(2\) を返す。
-
二つの文字列 \(A[1..n]\) と \(B[1..n]\) が与えられたときに、同じ添え字を使って \(A\) と \(B\) を単語の列に分割できるかどうかを判定する。例えば \(\color{maroon} \texttt{BOTH} \)\( \color{maroon} \texttt{EART} \)\( \color{maroon} \texttt{HAND} \)\( \color{maroon} \texttt{SATU} \)\( \color{maroon} \texttt{RNSPIN}\) と \(\color{maroon} \texttt{PINS} \)\( \color{maroon} \texttt{TART} \)\( \color{maroon} \texttt{RAPS} \)\( \color{maroon} \texttt{ANDR} \)\( \color{maroon} \texttt{AGSLAP} \) は次のように同じ添え字を使って単語の列に分割できるので、アルゴリズムは \(\textsc{True}\) を返す。 \[ \begin{gathered} \color{maroon}{\texttt{BOT} \cdot \texttt{HEART} \cdot \texttt{HAND} \cdot \texttt{SAT} \cdot \texttt{URNS} \cdot \texttt{PIN}} \\ \color{maroon}{\texttt{PIN} \cdot \texttt{START} \cdot \texttt{RAPS} \cdot \texttt{AND} \cdot \texttt{RAGS} \cdot \texttt{LAP}} \end{gathered} \]
-
二つの文字列 \(A[1..n]\) と \(B[1..n]\) が与えられたときに、同じ添え字を使って \(A\) と \(B\) 両方を単語の列に分割する方法の数を計算する。
-
-
配列 \(A[1..n]\) が与えられたとします。 \(A\) の要素は正、負、またはゼロの数であり、整数であるとは限りません。
-
連続する部分列 \(A[i..j]\) の和の最大値を求めるアルゴリズムを説明、解析してください。
-
連続する部分列 \(A[i..j]\) の積の最大値を求めるアルゴリズムを説明、解析してください。
例えば入力として配列 \([-6, 12, -7, 9, 14, -7, 5]\) が与えられたとき、一つ目の問題に対するアルゴリズムは 19 を返し、二つ目の問題に対するアルゴリズムは 504 を返します。

また、入力として一つの要素からなる配列 \([-374]\) が与えられたとき、一つ目の問題に対する答えのアルゴリズムは \(0\) を返し、二つ目の問題に対する答えのアルゴリズムは \(1\) を返します (空配列も部分列です!)。解析においては比較、加算、乗算演算の実行時間が \(O(1)\) であると仮定して構いません。
[ヒント: (a) は少なくとも 1980 年代中頃から使われている標準的な情報科学の面接試験の問題です。ウェブには回答がたくさん載っていますし、この問題に対する Wikipedia のページだってあります!しかし 2016 年時点では、ウェブで見つかる (b) に対する答えの大部分が、実行時間が最良のものより遅かったり、そもそも正しい答えを計算していなかったりします。]
-
-
この問題では前問の最大部分列問題の変種を考えます。全ての問題で入力は任意の実数の配列 \(A[1..n]\) であり、いくつかの問題では \(X \geq 0\) も入力に含まれます。
-
回り込み: \(A\) が環状 (circular) 配列だとします。この設定では "連続する部分列" が \(A[i..j]\) および \(A[i..n] \cdot A[1..j]\) を意味します。 \(A\) の連続する部分列の和の最大値を求めるアルゴリズムを説明、解析してください。
-
長い部分列だけ: 長さが \(X\) 以上の連続する部分列 \(A[i..j]\) の和の最大値を求めるアルゴリズムを説明、解析してください。
-
短い部分列だけ: 長さが \(X\) 以下の連続する部分列 \(A[i..j]\) の和の最大値を求めるアルゴリズムを説明、解析してください。
-
ザ・プライス・イズ・ライト: 和が \(X\) 以下の連続する部分列 \(A[i..j]\) の和の最大値を求めるアルゴリズムを説明、解析してください。
-
\(A\) の要素が非負であると仮定したときに、前問のアルゴリズムを高速化してください。
-
-
この問題では様々な種類の最適な部分列を見つける効率の良いアルゴリズムを作ってもらいます。部分列とは列からいくつかの要素を削除し、残った要素の順序を保ったまま並べたときに得られる列のことです。部分列の要素は元の列で連続している必要はありません。例えば \(\color{maroon}{\texttt{C}}\), \(\color{maroon}{\texttt{DAMN}}\), \(\color{maroon}{\texttt{YAIOAI}}\), \(\color{maroon}{\texttt{DYNAMICPROGRAMMING}}\) はみな \(\color{maroon}{\texttt{DYNAMICPROGRAMMING}}\) の部分列です。
[ヒント: 貪欲なアルゴリズムを使って \(O(n)\) 時間で解ける問題は一つだけです。]
-
\(A[1..m]\) と \(B[1..n]\) を任意の配列とします。 \(A\) と \(B\) の共通部分列 (common subsequence) とは、\(A\) の部分列でもあり \(B\) の部分列でもあるような配列を言います。 \(A\) と \(B\) の最長共通部分列の長さを計算する効率の良いアルゴリズムを説明してください。
-
\(A[1..m]\) と \(B[1..n]\) を任意の配列とします。 \(A\) と \(B\) の共通超配列 (common supersequence) とは、\(A\) と \(B\) の両方を部分列として含む配列のことを言います。 \(A\) と \(B\) の最短共通超配列の長さを計算する効率の良いアルゴリズムを説明してください。
-
配列 \(X[1..n]\) がバイトニック (bitonic) であるとは、ある添え字 \(i\ (1 < i < n)\) が存在して、接頭部分 \(X[1..i]\) が増加列で接尾部分 \(X[i..n]\) が減少列となること言います。与えられた整数の配列 \(A\) の最長バイトニック部分列の長さを計算する効率の良いアルゴリズムを説明してください。
-
配列 \(X[1..n]\) が振動している (oscillating) とは、全ての偶数 \(i\) について \(X[i] < X[i + 1]\) であり、全ての奇数 \(i\) について \(X[i] > X[i+1]\) であることを言います。与えられた整数の配列 \(A\) の最長振動部分列の長さを計算する効率の良いアルゴリズムを説明してください。
-
与えられた整数の配列 \(A\) の最短振動超配列の長さを計算する効率の良いアルゴリズムを説明してください。
-
配列 \(X[1..n]\) が凸 (convex) であるとは、全ての \(i\) について \(2 \cdot X[i] <\) \(X[i - 1] + X[i + 1]\) が成り立つことを言います。与えられた整数の配列 \(A\) の最長凸部分列の長さを計算する効率の良いアルゴリズムを説明してください。
-
\(X[1..n]\) が弱増加 (weakly increasing) であるとは、全ての要素が前二つの要素の平均よりも大きい、つまり全ての\(i>2\) について \(2 \cdot X[i] > X[i-1] + X[i-2]\) であることを言います。与えられた整数の配列 \(A\) の最長弱増加部分列の長さを計算する効率の良いアルゴリズムを説明してください。
-
\(X[1..n]\) が二重増加 (double increasing) であるとは、全ての \(i > 2\) に対して \(X[i] > X[i-2]\) が成り立つことを言います (言い換えれば、二重増加な配列とは二つの増加列を互い違いに並べたものです)。与えられた整数の配列 \(A\) の最長二重増加部分列の長さを計算する効率の良いアルゴリズムを説明してください。
-
\(X[1..n]\) が増加 (increasing) 列であるとは、全ての \(i\) について \(X[i] < X[i+1]\) であることを言いました。二つの整数配列が与えられたときに、最長共通増加部分列を計算する効率の良いアルゴリズムを説明してください。例えば \(\langle 3,\) \(1, \) \(4, \) \(1, \) \(5, \) \(9, \) \(2, \) \(6, \) \(5, \) \(3, \) \(5, \) \(8, \) \(9, \) \(7, \) \(9, \) \(3 \rangle\) と \(\langle 1, \) \(4, \) \(1, \) \(4, \) \(2, \) \(1, \) \(3, \) \(5, \) \(6, \) \(2, \) \(3, \) \(7, \) \(3, \) \(0, \) \(9, \) \(5 \rangle\) の最長共通増加部分列は \(\langle 1, \) \(4, \) \(5, \) \(6, \) \(7, \) \(9 \rangle\) です。
-
-
二つの文字列 \(X, Y\) のシャッフル (shuffle) とは、それぞれの文字を順番を保ったまま一つの文字列に合成したものを言います。例えば \(\color{maroon}{\texttt{BANANAANANAS}}\) は \(\color{#0071BB}{\texttt{BANANA}}\) と \(\color{maroon}{\texttt{ANANAS}}\) のシャッフルであり、考えられる組み合わせ方は何種類かあります: \[ \color{#0071BB}{\texttt{BANANA}}\color{maroon}{\texttt{ANANAS}} \quad \color{#0071BB}{\texttt{BAN}}\color{maroon}{\texttt{ANA}} \color{#0071BB}{\texttt{ANA}}\color{maroon}{\texttt{NAS}} \quad \color{#0071BB}{\texttt{B}}\color{maroon}{\texttt{AN}} \color{#0071BB}{\texttt{AN}}\color{maroon}{\texttt{A}} \color{#0071BB}{\texttt{A}}\color{maroon}{\texttt{NA}} \color{#0071BB}{\texttt{NA}}\color{maroon}{\texttt{S}} \] 同様に、\(\color{maroon}{\texttt{PRODGYRNAMAMMIINCG}}\) と \(\color{maroon}{\texttt{DYPRONGARMAMMICING}}\) はどちらも \(\color{#0071BB}{\texttt{DYNAMIC}}\) と \(\color{maroon}{\texttt{PROGRAMMING}}\) のシャッフルです: \[ \color{maroon}{\texttt{PRO}} \color{#0071BB}{\texttt{D}} \color{maroon}{\texttt{G}} \color{#0071BB}{\texttt{Y}} \color{maroon}{\texttt{R}} \color{#0071BB}{\texttt{NAM}} \color{maroon}{\texttt{AMMI}} \color{#0071BB}{\texttt{I}} \color{maroon}{\texttt{N}} \color{#0071BB}{\texttt{C}} \color{maroon}{\texttt{G}} \quad \color{#0071BB}{\texttt{DY}} \color{maroon}{\texttt{PRO}} \color{#0071BB}{\texttt{N}} \color{maroon}{\texttt{G}} \color{#0071BB}{\texttt{A}} \color{maroon}{\texttt{R}} \color{#0071BB}{\texttt{M}} \color{maroon}{\texttt{AMM}} \color{#0071BB}{\texttt{IC}} \color{maroon}{\texttt{ING}} \]
-
三つの文字列 \(A[1..m], B[1..n], C[1..m+n]\) が与えられたときに、\(C\) が \(A\) と \(B\) のシャッフルであるかどうかを判定するアルゴリズムを説明、解析してください。
-
\(X\) と \(Y\) の滑らか (smooth) なシャッフルとは、両方の文字列について文字が三つ以上連続して使われることがないシャッフルのことを言います。例えば:
- \(\color{maroon}{\texttt{PR}} \color{#0071BB}{\texttt{D}} \color{maroon}{\texttt{O}} \color{#0071BB}{\texttt{Y}} \color{maroon}{\texttt{G}} \color{#0071BB}{\texttt{NA}} \color{maroon}{\texttt{RA}} \color{#0071BB}{\texttt{M}} \color{maroon}{\texttt{MM}} \color{#0071BB}{\texttt{I}} \color{maroon}{\texttt{I}} \color{#0071BB}{\texttt{C}} \color{maroon}{\texttt{NG}}\) は \(\color{#0071BB}{\texttt{DYNAMIC}}\) と \(\color{maroon}{\texttt{PROGRAMMING}}\) の滑らかなシャッフルです。
- \(\color{#0071BB}{\texttt{DY}} \color{maroon}{\texttt{PR}} \color{#0071BB}{\texttt{N}} \color{maroon}{\texttt{OGR}} \color{#0071BB}{\texttt{A}} \color{maroon}{\texttt{A}} \color{#0071BB}{\texttt{M}} \color{maroon}{\texttt{MM}} \color{#0071BB}{\texttt{IC}} \color{maroon}{\texttt{ING}}\) は \(\color{#0071BB}{\texttt{DYNAMIC}}\) と \(\color{maroon}{\texttt{PROGRAMMING}}\) の滑らかなシャッフルではありません (三文字以上が連続した文字列 \(\color{maroon}{\texttt{OGR}}\) と \(\color{maroon}{\texttt{ING}}\) があるからです)。
- \(\color{#0071BB}{\texttt{XX}} \color{maroon}{\texttt{X}} \color{#0071BB}{\texttt{X}} \color{maroon}{\texttt{X}} \color{#0071BB}{\texttt{X}} \color{maroon}{\texttt{XX}} \color{#0071BB}{\texttt{XX}} \color{maroon}{\texttt{XX}} \color{#0071BB}{\texttt{XX}} \color{maroon}{\texttt{X}} \color{#0071BB}{\texttt{X}} \color{maroon}{\texttt{X}} \color{#0071BB}{\texttt{XX}}\) は \(\color{#0071BB}{\texttt{XXXXXXXXXXX}}\) と \(\color{maroon}{\texttt{XXXXXXXX}}\) の滑らかなシャッフルです。
- \(\color{#0071BB}{\texttt{XXXX}}\) と \(\color{maroon}{\texttt{XXXXXXXXXXXX}}\) の滑らかなシャッフルは存在しません。
三つの文字列 \(X[1..m], Y[1..n], Z[1..m+n]\) が与えられたときに、\(Z\) が \(X\) と \(Y\) の滑らかなシャッフルであるかどうかを判定するアルゴリズムを説明、解析してください。
-
-
この問題では入力を \(X[1..k], Y[i..n]\) (\(k \leq n\)) とします。
-
\(X\) が \(Y\) の部分列であるかを判定するアルゴリズムを説明、解析してください。例えば文字列 \(\color{maroon}{\texttt{PPAP}}\) は文字列 \(\color{#0071BB}{\texttt{P}} \color{maroon}{\texttt{EN}} \color{#0071BB}{\texttt{P}} \color{maroon}{\texttt{INE}} \color{#0071BB}{\texttt{A}} \color{maroon}{\texttt{PPLEAPPLE}} \color{#0071BB}{\texttt{P}} \color{maroon}{\texttt{EN}}\) の部分列です。
-
\(Y\) から要素を取り除いて \(X\) を \(Y\) の部分列でなくなるようにするとき、取り除かなくてはならない最小の要素数を求めるアルゴリズムを説明、解析してください。同じことですが、\(X\) の超配列でない \(Y\) の部分列のうち最長のものを求めるアルゴリズムを考えても良いです。例えば \(\color{maroon}{\texttt{PENPINE}} \color{#0071BB}{\texttt{A}} \color{maroon}{\texttt{PPLE}} \color{#0071BB}{\texttt{A}} \color{maroon}{\texttt{PPLEPEN}}\) から \(\color{#0071BB}{\texttt{AA}}\)を取り除いた文字列は \(\color{maroon}{\texttt{PPAP}}\) を部分列として持ちません。
-
❤ \(Y\) の互いに重ならない二つの部分列の両方に \(X\) が含まれることがあるかを判定するアルゴリズムを説明、解析してください。例えば \(\color{maroon}{\texttt{PPAP}}\) は \(\color{#0071BB}{\texttt{P}} \color{maroon}{\texttt{EN}} \color{#0071BB}{\texttt{P}} \color{maroon}{\texttt{INE}} \color{#0071BB}{\texttt{A}} \color{green}{\texttt{PP}} \color{maroon}{\texttt{LE}} \color{green}{\texttt{A}} \color{#0071BB}{\texttt{P}} \color{maroon}{\texttt{PLE}} \color{green}{\texttt{P}} \color{maroon}{\texttt{EN}}\) の二つの互いに重ならない部分列に含まれます。
-
追加の入力として実数の配列 \(C[1..n]\) が与えられ、\(C[i]\) が \(Y[i]\) のコストを表すとします。 \(Y\) の部分列 \(X\) のうちコストが最小のものを計算するアルゴリズムを説明、解析してください。つまり、全ての \(j\) に対して \(I[j] < I[j+1]\) かつ \(X[j] = Y[I[j]]\) となるような \(I[1..k]\) のうち、コスト \(\sum_{j=1}^{k}C[I[j]]\) が最小になるものを求めるアルゴリズムです。
-
\(Y\) の部分列に \(X\) がいくつあるか計算するアルゴリズムを説明、解析してください。カウントする部分列どうしは重なっていても構いません。解析をするときには任意の桁の二つの整数の足し算が \(O(1)\) 時間でできると仮定して構いません。例えば \(\color{maroon}{\texttt{PPAP}}\) は \(\color{maroon}{\texttt{PENPINEAPPLEAPPLEPEN}}\) の中にちょうど 23 個あります。また \(X\) と \(Y\) の文字が全て同じ場合、答えは \(\binom{n}{k}\) です。
-
\(l\) 桁の数の加算演算が \(O(l)\) 時間かかるとして、(e) のアルゴリズムの実行時間を求めてください。
-
-
入力された文字列 \(T[1..n]\) の連続する部分文字列で、逆順にしたものもまた \(T\) の連続する部分文字列であるもののうち最長なものの長さを求める効率の良いアルゴリズムを説明、解析してください。正順と逆順の文字列は重なってはいけません。例えば:
-
入力が \(\color{maroon}{\texttt{ALGORITHM}}\) の場合、答えは \(0\) です。
-
入力が \(\color{maroon}{\underline{\texttt{R}} \texttt{ECU} \underline{\texttt{R}} \texttt{SION}}\) の場合、条件を満たす部分文字列 \(\color{maroon}{\texttt{R}}\) があるので、 答えは \(1\) です。
-
入力が \(\color{maroon}{\texttt{R} \underline{\texttt{EDI}} \texttt{V} \underline{\texttt{IDE}}}\) の場合、条件を満たす部分文字列 \(\color{maroon}{\texttt{EDI}}\) があるので、答えは \(3\) です。答えとなる部分文字列とその逆順は重なってはいけないことに注意してください。
-
入力が \(\color{maroon}\texttt{D} \underline{\texttt{YNAM}}\)\(\color{maroon} \texttt{ICPROGRAMMING}\)\(\color{maroon}\underline{\texttt{MANY}} \texttt{TIMES}\) の場合、条件を満たす部分文字列 \(\color{maroon}{\texttt{YNAM}}\) があるので、答えは \(4\) です。文字列 \(\color{maroon}{\texttt{YNAMIR}}\) は連続していないので条件を満たしません。
-
-
回文 (palindrome) とは左から読んでも右から読んでも同じになる文字列のことを言います。例えば \(\color{maroon}{\texttt{I}}\), \(\color{maroon}{\texttt{DEED}}\), \(\color{maroon}\texttt{RACECAR}\), \(\color{maroon}\texttt{AMANAPL}\)\(\color{maroon}\texttt{ANACATACA}\)\(\color{maroon}\texttt{NALPANAMA}\) は全て回文です。
-
与えられた文字列の最長回文部分列の長さを求める効率の良いアルゴリズムを説明、解析してください。例えば文字列 \(\texttt{{\color{#0071BB}M}{\color{maroon}A}{\color{#0071BB}H}{\color{maroon}D}}\)\(\texttt{{\color{#0071BB}Y}{\color{maroon}NA}{\color{#0071BB}M}{\color{maroon}ICP}}\)\(\texttt{{\color{#0071BB}RO}{\color{maroon}G}{\color{#0071BB}R}}\)\(\texttt{{\color{maroon}AMZLET}{\color{#0071BB}M}}\)\(\texttt{{\color{maroon}ESHOW}{\color{#0071BB}Y}{\color{maroon}OUT}}\)\(\texttt{{\color{#0071BB}H}{\color{maroon}E}{\color{#0071BB}M}}\) の最長回文部分列は \({\color{#0071BB}\texttt{MHYMRORMYHM}}\) なので、アルゴリズムの答は \(11\) です。
-
与えられた文字列の最短回文超配列の長さを求める効率の良いアルゴリズムを説明、解析してください。例えば \(\color{#0071BB}{\texttt{TEWNTYONE}}\) の最短回文超配列は \(\texttt{{\color{#0071BB}TWENT}{\color{maroon}O}{\color{#0071BB}YO}{\color{maroon}T}{\color{#0071BB}NE}{\color{maroon}WT}}\) なので、アルゴリズムの答は \(13\) です。
-
任意の文字列は回文の列に分解できます。例えば文字列 \(\color{maroon}{\texttt{BUBB}}\)\(\color{maroon}{\texttt{ASEES}}\)\(\color{maroon}{\texttt{ABANANA}}\) ("Bubba sees a banana") は次のように分解できます (分解の仕方はこの他に \(65\) 通りあります): \[ \begin{gathered} \color{maroon}{\texttt{BUB}} \cdot \color{maroon}{\texttt{BASEESAB}} \cdot \color{maroon}{\texttt{ANANA}} \\ \color{maroon}{\texttt{B}} \cdot \color{maroon}{\texttt{U}} \cdot \color{maroon}{\texttt{BB}} \cdot \color{maroon}{\texttt{ASEESA}} \cdot \color{maroon}{\texttt{B}} \cdot \color{maroon}{\texttt{ANANA}} \\ \color{maroon}{\texttt{BUB}} \cdot \color{maroon}{\texttt{B}} \cdot \color{maroon}{\texttt{A}} \cdot \color{maroon}{\texttt{SEES}} \cdot \color{maroon}{\texttt{ABA}} \cdot \color{maroon}{\texttt{N}} \cdot \color{maroon}{\texttt{ANA}} \\ \color{maroon}{\texttt{B}} \cdot \color{maroon}{\texttt{U}} \cdot \color{maroon}{\texttt{BB}} \cdot \color{maroon}{\texttt{A}} \cdot \color{maroon}{\texttt{S}} \cdot \color{maroon}{\texttt{EE}} \cdot \color{maroon}{\texttt{S}} \cdot \color{maroon}{\texttt{A}} \cdot \color{maroon}{\texttt{B}} \cdot \color{maroon}{\texttt{A}} \cdot \color{maroon}{\texttt{NAN}} \cdot \color{maroon}{\texttt{A}} \\ \color{maroon}{\texttt{B}} \cdot \color{maroon}{\texttt{U}} \cdot \color{maroon}{\texttt{B}} \cdot \color{maroon}{\texttt{B}} \cdot \color{maroon}{\texttt{A}} \cdot \color{maroon}{\texttt{S}} \cdot \color{maroon}{\texttt{E}} \cdot \color{maroon}{\texttt{E}} \cdot \color{maroon}{\texttt{S}} \cdot \color{maroon}{\texttt{A}} \cdot \color{maroon}{\texttt{B}} \cdot \color{maroon}{\texttt{A}} \cdot \color{maroon}{\texttt{N}} \cdot \color{maroon}{\texttt{A}} \cdot \color{maroon}{\texttt{N}} \cdot \color{maroon}{\texttt{A}} \end{gathered} \] 与えられた文字列を回文に分解するときに、最低でも必要となる回文の数を計算する効率の良いアルゴリズムを説明、解析してください。例えば \(\color{maroon}{\texttt{BUBBASEESABANANA}}\) に対するアルゴリズムの答えは \(3\) です。
-
与えられた文字列をなるべく長い回文を使って分解するときに、使うことになる最短の回文の長さの最大値を求める効率の良いアルゴリズムを説明、解析してください。例えば:
-
入力 \(\color{maroon}{\texttt{PALINDROME}}\) に対する出力は \(1\) です。
-
入力 \(\color{maroon}{\texttt{BUBBASEESABANANA}}\) に対する出力は、\(\color{maroon}{\texttt{BUB}} \cdot \color{maroon}{\texttt{BASEESAB}} \cdot \color{maroon}{\texttt{ANANA}}\) に対応する \(3\) です。
-
同じ文字が \(n\) 個並んだ文字列に対する出力は \(n\) です。
-
-
与えられた文字列を回文に分解する方法が何通りあるかを計算する効率の良いアルゴリズムを説明、解析してください。例えば:
-
入力 \(\color{maroon}{\texttt{PALINDROME}}\) に対する出力は \(1\) です。
-
入力 \(\color{maroon}{\texttt{BUBBASEESABANANA}}\) に対する出力は \(70\) です。
-
同じ文字が \(n\) 個並んだ文字列に対する出力は \(2^{n-1}\) です。
-
-
❤ ある文字列に対するメタ回文 (metapalindrome) とは、その文字列の回文への分解であって、分解した回文の長さからなる列も回文になっているものを言います。例えば \[ \color{maroon}{\texttt{BOB}} \cdot \color{maroon}{\texttt{S}} \cdot \color{maroon}{\texttt{MAM}} \cdot \color{maroon}{\texttt{ASEESA}} \cdot \color{maroon}{\texttt{UKU}} \cdot \color{maroon}{\texttt{L}} \cdot \color{maroon}{\texttt{ELE}} \] はメタ回文です。なぜなら \(\color{maroon}{\texttt{BOBSMAMASEESAUKULELE}}\) の回文への分解であり、回文の長さからなる列 \((3,1,3,6,3,1,3)\) が回文だからです。与えられた文字列に対する最短のメタ回文の長さを求める効率の良いアルゴリズムを説明、解析してください。例えば入力 \(\color{maroon}{\texttt{BOBSMAMASEESAUKULELE}}\) に対するアルゴリズムの出力は \(7\) です。
-
-
正の整数の配列 \(A[1..n]\) が与えられたとします。 \(A\) の前後増加部分列 (increasing back-and-forth subsequence) とは、添え字の配列 \(I[1..l]\) であって次の条件を満たすものを言います:
- 任意の \(j\) について \(1 \leq I[j] \leq n\)
- 任意の \(j\) について \(A[I[j]] < A[I[j+1]]\)
- \(I[j]\) が偶数ならば \(I[j+1] > I[j]\)
- \(I[j]\) が奇数ならば \(I[j+1] < I[j]\)
もう少し崩して言うと、次のようになります: 正の整数が入った \(n\) 個の箱が一列に並んでいるとします。一つの箱を選び、それが奇数番目の箱なら今の箱より左にある箱のなかで今よりも大きい数の入ったものに移動し、偶数番目の箱なら今の箱より右にある箱のなかで今よりも大きい数の入ったものに移動します。この移動を繰り返したときの添え字の列が前後増加部分列です。
与えられた \(n\) 要素の配列の最長前後増加部分列の長さを求める効率の良いアルゴリズムを説明、解析してください。例えば

という配列が入力されたとき、アルゴリズムは次の前後増加部分列に対応する \(9\) を答えます:

-
一段落の英語の文章を紙上に (どうしてもと言うなら、コンピューターのスクリーン上に) 組版したいとします。段落には \(n\) 個の単語が含まれ、\(i\) 番目の単語の長さは \(l[i]\) だとします。この単語列を長さがちょうど \(L\) の行に分割することが目標です。
段落がどのように行に分割されるかに応じて、単語間の空白の幅を調整しなければなりません。なぜなら段落は両端揃えである、つまり各行の右端の余白と段落の最初を除いた各行の左端の余白が揃っている必要があるからです。また同じ行にある単語の間には一単位以上の空白が必要です。
段落のレイアウトのあふれ (slop) を次のように定義します: 最後の行を除く各行について、その行に含まれる "追加の" 空白の数、つまり実際に含まれる空白の数からその行にある単語の間の数を引いたもの、の三乗を求め、その和を段落のレイアウトのあふれとします。式で書くと、\(i\) 番目の単語から \(j\) 番目の単語が含まれる行のあふれは \((L - j + i - \sum_{k=i}^{j} l[k])^{3}\) と定義されます。あふれが最小となるように段落を印刷する動的計画法のアルゴリズムを説明してください。
-
あなたは 8 才の甥 Elmo と単純なゲームを遊ぶことになりました。このゲームはカードを一列に並べた状態から始まり、あなたと Elmo は順番に左端または右端からカードを取っていきます。カードがなくなった時点でゲームは終了で、持っているカードのポイントの和が大きい方が勝ちです。
Elmo はアルゴリズムの講義を取ったことがないので、常に選択できる二枚のカードのうち大きな方を選択するという、単純な貪欲戦術を使います。この問題の目標は可能な場合には必ず Elmo に勝利する戦略を見つけることです (子供をこんな風に負かすのは大人げないかもしれませんが、 Elmo は手を抜いた大人に勝たせてもらうのが大嫌いです) 。
-
あなたは貪欲な戦略を使うべきでないことを示してください。つまり、貪欲な戦略に従わなかった場合にのみ勝てるゲームがあることを示してください。
-
与えられたカードの初期状態について、Elmo を相手に勝負をしたときに集められる最高得点を計算するアルゴリズムを説明、解析してください。
-
♣ Elmo が 4 才のときに使っていた戦略はもっと単純で、両端のカードのどちらかを一様ランダムに選ぶというものでした。つまり、彼のターンが回ってきたときに二つのカードが残っているならば、左端のカードを \(\frac{1}{2}\) の確率で、右端のカードを \(\frac{1}{2}\) の確率で選ぶということです。与えられたカードの初期状態について、4 才の Elmo を相手に勝負したときに集められる得点の期待値の最大値を計算するアルゴリズムを説明してください。
-
5 年後、 13 才になった Elmo は格段に強い完璧なプレイヤーになりました。与えられたカードの初期状態について、完璧な相手と勝負したときに集められる最高得点を計算するアルゴリズムを説明、解析してください。
-
-
あなたの flippin' sweet なダンスのスキルを見せつけるときが迫ってきました!明日大きなダンス大会があり、あなたはその大会のために人生をかけて準備をしてきました (アラスカで伯父とクズリ狩りをしていた時間は除く)。あなたは \(n\) 人の審査員それぞれがコンテストでかける \(n\) 曲を時系列順に並べたリストを前もって手に入れることに成功しました。 Yesssssssssss!
あなたは全ての曲と審査員と自分のダンスの上手さについてとてもよく理解しているので、 任意の \(k\) について \(k\) 番目の曲を踊った場合の点数が \(\mathit{Score}[k]\) であることを知っています。また \(\mathit{Score}[k]\) 点を獲得するために \(k\) 番目の曲を踊った場合、疲れてしまうので次の \(\mathit{Wait}[k]\) 曲では踊ることができません (\(k+1\) 番目の曲から \(k+\mathit{Wait}[k]\) 番目までの曲で踊れないということです)。合計点数が一番大きいダンサーがコンテストで優勝するので、あなたは合計点数はなるべく高くしたいと思っています。
取得できる最高得点を計算する効率の良いアルゴリズムを説明、解析してください。あなたの sweet なアルゴリズムに対する入力は配列の組 \(\mathit{Score}[1..n]\), \(\mathit{Wait}[1..n]\) です。
-
新作のスワップパズルゲーム Candy Swap Saga XIII には \(1\) から \(n\) までの数字がついた \(n\) 匹のかわいい動物が出てきます。この動物達は circus peanuts, Heath bars, Cioccolateria Gardini chocolate truffles という三つのアメのうちどれか一つを持っています。あなたは最初 circus peanut を持っている状態でゲームが始まります。
あなたは動物を \(1\) から \(n\) まで順番に訪ね、動物とアメを交換することでポイントを獲得していきます:
-
自分の持っているアメと同じ種類のアメと交換したとき、ポイントを獲得する。
-
自分の持っているアメと違う種類のアメと交換したとき、ポイントを失う (ポイントは負になりうる)。
-
交換をしなかった場合、ポイントは変わらない。
あなたは \(n\) 匹の動物を順番通りに訪れなくてはならず、一度訪れた動物を再び訪れることはできません。
獲得可能な最高得点を計算する効率の良いアルゴリズムを説明、解析してください。アルゴリズムに対する入力は \(C[1..n]\) であり、\(C[i]\) が \(i\) 番目の動物が持っているアメの種類を表します。
-
-
新設される Maksymilian R. Levchin 情報科学大学に学部長として着任することになっている Lenny Rutenbar は、 Orchard Donws そりゲレンデの南コースに20小さな雪のジャンプ台をいくつか作らせ、電子計算工学科の学科長 Bill Kudeki にそり対決を申し入れました。Bill と Lenny はコースをそりで滑り降り、滞空距離を競います。勝者は Siebel Center と新設の ECE 棟を学部/学科のものにできますが、敗者は学部/学科全体を Loomis Lab の隣にある Boneyard 排水渠に移動させなければなりません。
Lenny および Bill がジャンプ台に差し掛かったときに地上にいるなら、ジャンプ台を使ってジャンプをするか通り過ぎるかを選択できます。当然ジャンプ台は滞空時には使えないので、ジャンプをした場合には以降のジャンプ台をいくつか見逃す可能性があります。
-
配列の組 \(\mathit{Ramp}[1..n]\) と \(\mathit{Length}[1..n]\) が与えられ、\(\mathit{Ramp}[i]\) が頂上から \(i\) 番目のジャンプ台までの距離を表し、\(\mathit{Length}[i]\) が \(i\) 番目のジャンプ台でジャンプしたそりが滞空する距離を表すとします。Lenny または Bill の最大滞空距離を計算するアルゴリズムを説明、解析してください。
-
Lenny と Bill の小さな賭け事について耳にした大学の弁護士はこの対決について異議を唱えました。とどまることを知らない保険料率と訴訟から大学を守るために、弁護士は二人がジャンプできる回数に上限を設けました。前問の \(\mathit{Ramp}[1..n]\) と \(\mathit{Length}[1..n]\) に加えて \(k\) が与えられ、ジャンプが最大 \(k\) 回しか許されていない場合に、Lenny または Bill の最大滞空距離を計算するアルゴリズムを説明、解析してください。
-
❤ ジャンプの回数に上限を設けても対決が取りやめにならなかったのを見て、弁護士はさらなる制限を加えました: どのジャンプ台も一度しか使われてはいけないというのです!法律の干渉にうんざりした Lenny と Bill は賭けを諦め、その代わり協力して観客が楽しめる滑りをすることを決めました。前問の設定に加えて二人が同じジャンプ台を使えないとしたときに、二人の滞空距離の和の最大値を求めるアルゴリズムを説明、解析してください。
-
-
農家の Boggis, Bunce, Bean は Mr. Fox のために障害物コースをこしらえました。コースは一列に並んだブースでできており、各ブースには明るい赤で番号が書いてあります。きちんと言うと、Mr. Fox には実数の配列 \(A[1..n]\) が与えられ、\(A[i]\) が \(i\) 個目のブースに書かれた番号を表します。 三人の農家と Mr. Fox は次のルールに従います:
-
Mr. Fox はブースに入るたびに "Ring!" と "Ding!" のどちらかを必ず言う。
-
\(i\) 番目のブースで "Ring!" と言った場合、\(A[i]\) 個のチキンを得る ( \(A[i] < 0\) のときは \(-\ A[i]\) 個のチキンを失う)。
-
\(i\) 番目のブースで "Ding!" と言った場合、\(A[i]\) 個のチキンを失う ( \(A[i] < 0\) のときは \(-\ A[i]\) 個のチキンを得る)。
-
Mr. Fox は四つのブース連続で同じ単語を言うことはできない。例えば 6, 7, 8 番目のブースで "Ring!" と言ったなら、9 番目のブースでは "Ding!" と言わなければならない。
-
獲得したチキンの清算は全てのブースを訪れ、審判が "Hot box!" と言った後に行われる。Mr. Fox は障害物コースをチキンをもって回る必要はない。
-
Mr. Fox がルールを破った場合、あるいは障害物コースを完走した時点で農家にチキンの貸しがある場合、農家は Mr. Fox を銃で撃つ。
与えられる配列 \(A[1..n]\) で表される障害物コースを走ったときに Mr. Fox が獲得できるチキンの数の最大値を計算するアルゴリズムを説明、解析してください。 [ヒント: 燃えた松ぼっくりに注意!]
-
-
ダンスダンスレボリューション (Dance Dance Revolution) は日本のゲーム会社コナミによって 1998 年に制作されたダンスゲームです。プレイヤーは上下左右の矢印が足元に書かれた舞台に立ち、ゲーム画面下から上に流れる矢印 (\(\leftarrow, \uparrow, \downarrow, \rightarrow\)) が画面の一番上に来た時にタイミングよくステップを踏むというゲームです (矢印は画面の一番上に来たときにちょうど曲の拍に合うように流れてきます)。
このゲームの変種 "Vogue Vogue Revolution" の目標は、動きを最小限にしつつ完璧にプレイすることです。矢印が画面の一番上に来たときに足が元々その矢印の上にあるなら、体を動かさずに済むことに対して \(1\) スタイルポイントが与えられます。もし踏まなければならない矢印に両方の足が無い場合は、ちょうど一つの足をその矢印の場所に移動させます。間違った矢印に足を動かした場合、正しい矢印を踏めなかった場合、足が正しい位置にあるのに足を動かした場合にはスタイルポイントを全て失ってゲームオーバーとなります。
どうすればスタイルポイントを最大化できるでしょうか? この問題ではスタート時点で左足は \(\leftarrow\) に、右足は \(\rightarrow\) にあり、 プレイヤーは流れてくる矢印を完全に記憶しているとします。例えば \(\uparrow \uparrow \downarrow \downarrow \leftarrow \rightarrow \leftarrow \rightarrow\) に対しては、次のようなステップで \(5\) スタイルポイントを獲得できます。

-
任意の \(n\) 個の矢印の列に対して、 少なくとも \(n/4 - 1\) スタイルポイントを獲得できることを示してください。
-
VVR の譜面に対して獲得可能な最大のスタイルポイントを計算する効率の良いアルゴリズムを説明してください。入力は矢印の向きの配列 \(\mathit{Arrow}[1..n]\) です。
-
-
次の一人遊びのスクラブルを考えます。ゲームはアルファベットと数字が書かれたタイルの有限列をテーブルの上に置いた状態で始まり、ゲームの開始とともにプレイヤーはタイル列から最初の七つのタイルを手札に加えます。各ターンで、プレイヤーは手札のタイルの一部もしくは全部を使って英単語を作り、そのタイルに書かれている数字だけ点数を獲得します (手札から英単語を作れないならそこでゲーム終了です)。英単語を作った後は次の条件のいずれかが成り立つまでタイルをタイル列から手札に加えます (a) 手札が七枚になる (b) タイル列が空になる (ダブル/トリプルワードやビンゴ、ブランク、パスはありません)。目標はなるべく多くの得点を獲得することです。
例えば、次の 20 個のタイルからなるタイル列を考えます: \[ | {\color{maroon}{\texttt{I}}_{2}} | {\color{maroon}{\texttt{N}}_{2}} | {\color{maroon}{\texttt{X}}_{8}} | {\color{maroon}{\texttt{A}}_{1}} | {\color{maroon}{\texttt{N}}_{2}} | {\color{maroon}{\texttt{A}}_{1}} | {\color{maroon}{\texttt{D}}_{3}} | {\color{maroon}{\texttt{U}}_{5}} | {\color{maroon}{\texttt{D}}_{3}} | {\color{maroon}{\texttt{I}}_{2}} | {\color{maroon}{\texttt{D}}_{3}} | {\color{maroon}{\texttt{K}}_{8}} | {\color{maroon}{\texttt{U}}_{5}} | {\color{maroon}{\texttt{B}}_{4}} | {\color{maroon}{\texttt{L}}_{2}} | {\color{maroon}{\texttt{A}}_{1}} | {\color{maroon}{\texttt{K}}_{8}} | {\color{maroon}{\texttt{H}}_{5}} | {\color{maroon}{\texttt{A}}_{1}} | {\color{maroon}{\texttt{N}}_{2}} | \] このタイル列からゲームを開始した場合、次のようにすると 68 点を獲得できます。
- 手札が \(|{\color{maroon}{\texttt{I}}_{2}} | {\color{maroon}{\texttt{N}}_{2}} | {\color{maroon}{\texttt{X}}_{8}} | {\color{maroon}{\texttt{A}}_{1}} | {\color{maroon}{\texttt{N}}_{2}} | {\color{maroon}{\texttt{A}}_{1}} | \color{maroon}{\texttt{D}}_{3} |\) と初期化される。
- \(|{\color{maroon}{\texttt{N}}_{2}} | {\color{maroon}{\texttt{A}}_{1}} | {\color{maroon}{\texttt{I}}_{2}} | {\color{maroon}{\texttt{A}}_{1}} | {\color{maroon}{\texttt{D}}_{3}} |\) を出して 9 点を得る。手札には \(|{\color{maroon}{\texttt{N}}_{2}} | {\color{maroon}{\texttt{X}}_{8}} |\) が残る。
- 次の 5 枚のタイル \(|{\color{maroon}{\texttt{U}}_{5}} | {\color{maroon}{\texttt{D}}_{3}} | {\color{maroon}{\texttt{I}}_{2}} | {\color{maroon}{\texttt{D}}_{3}} | {\color{maroon}{\texttt{K}}_{8}} |\) を手札に加える。
- \(|{\color{maroon}{\texttt{U}}_{5}} | {\color{maroon}{\texttt{N}}_{2}} | {\color{maroon}{\texttt{D}}_{3}} | {\color{maroon}{\texttt{I}}_{2}} | {\color{maroon}{\texttt{D}}_{3}} |\) を出して 15 点を得る。手札には \(|{\color{maroon}{\texttt{K}}_{8}} | {\color{maroon}{\texttt{X}}_{8}} |\) が残る。
- 次の 5 枚のタイル \(|{\color{maroon}{\texttt{U}}_{5}} | {\color{maroon}{\texttt{B}}_{4}} | {\color{maroon}{\texttt{L}}_{2}} | {\color{maroon}{\texttt{A}}_{1}} | {\color{maroon}{\texttt{K}}_{8}} |\) を手札に加える。
- \(|{\color{maroon}{\texttt{B}}_{4}} | {\color{maroon}{\texttt{U}}_{5}} | {\color{maroon}{\texttt{L}}_{2}} | {\color{maroon}{\texttt{K}}_{8}} |\) を出して 19 点を得る。手札には \(|{\color{maroon}{\texttt{K}}_{8}} | {\color{maroon}{\texttt{X}}_{8}} | {\color{maroon}{\texttt{A}}_{1}} |\) が残る。
- 次の三枚のタイル \(|{\color{maroon}{\texttt{H}}_{5}} | {\color{maroon}{\texttt{A}}_{1}} | {\color{maroon}{\texttt{N}}_{2}} |\) を手札に加える。
- \(|{\color{maroon}{\texttt{A}}_{1}} | {\color{maroon}{\texttt{N}}_{2}} | {\color{maroon}{\texttt{K}}_{8}} | {\color{maroon}{\texttt{H}}_{5}} |\) を出して 16 点を得る。
- \(|{\color{maroon}{\texttt{A}}_{1}} | {\color{maroon}{\texttt{X}}_{8}} |\) を出して 9 点を得る。手札が空になったのでゲーム終了。
このゲームについて、次の問題に答えてください。
-
タイル列が \(\mathit{Letter}[1..n]\) と \(\mathit{Value}[\texttt{A}..\texttt{Z}]\) で定義されるとします。ここで \(\mathit{Letter}[1..n]\) には \(\texttt{A}\) から \(\texttt{Z}\) までの文字が格納され、\(\mathit{Value}[l]\) は文字 \(l\) の点数を表します (この問題では同じ文字は全て同じ点数を持つとします)。与えられたタイル列における最高得点を計算する効率の良いアルゴリズムを説明、解析してください。
-
同じ文字でも異なる点数を持つことを許すことにします。このとき入力は \(\mathit{Letter}[1..n]\) と \(\mathit{Value}[1..n]\) であり、\(\mathit{Value}[i]\) が \(i\) 番目のタイルの点数を表します。与えられたタイル列における最高得点を計算する効率の良いアルゴリズムを説明、解析してください。
両方の問題において、アルゴリズムの出力は可能な最高得点を表す数字です。また手札にある七枚のタイルから作れる全ての英単語とその点数を \(O(1)\) 時間で計算できるとして構いません (実際できるので)。
-
平面上の \(n\) 個の線分の集合 \(L\) を考えます。全ての線分は \(y=0\) 上の点と \(y=1\) 上の点を結んでいて、\(2n\) 個の端点は重ならないとします。
-
どの線分も交わらない \(L\) の部分集合で最大のものを計算するアルゴリズムを説明、解析してください。
-
全ての線分の組が交わるような \(L\) の部分集合で最大のものを計算するアルゴリズムを説明、解析してください。
今度は平面上の \(n\) 個の線分の集合 \(L\) で、全ての線分の端点が単位円 \(x^{2} + y^{2} = 1\) 上にあり、\(2n\) 個の端点が重ならないものを考えます。
-
どの線分も交わらない \(L\) の部分集合で最大のものを計算するアルゴリズムを説明、解析してください。
-
全ての線分の組が交わるような \(L\) の部分集合で最大のものを計算するアルゴリズムを説明、解析してください。
-
-
\(P\) を単位円周上に均等に分布した \(n\) 個の点、\(S\) を両端点が \(P\) に含まれる \(m\) 個の線分の集合とします。 \(S\) に含まれる \(m\) 個の線分の両端点は重ならないとは限りません。また \(n\) は \(2m\) より極端に小さい可能性があります。
-
含まれるどの線分の組も共通元を持たない \(S\) の部分集合のうち最大のものを計算するアルゴリズムを説明、解析してください。線分の組が共通元を持たない (disjoint である) とは、共通の点が端点を含めて無いことを言います。
-
含まれるどの線分の組も内部に共通元を持たない \(S\) の部分集合のうち最大のものを計算するアルゴリズムを説明、解析してください。線分の組が内部に共通元を持たない (interior-disjoint である) とは、共通の点が全く無いか、あっても端点一つだけであることを言います。
-
含まれるどの線分の組も交わる \(S\) の部分集合のうち最大のものを計算するアルゴリズムを説明、解析してください。交点が端点であっても構いません。
-
含まれるどの線分の組も交差する \(S\) の部分集合のうち最大のものを計算するアルゴリズムを説明、解析してください。線分の組が交差 (cross) するとは、交わってかつ交点が端点でないことを言います。
満点のためには、四つのアルゴリズムは全て \(O(mn)\) 時間で実行されることが求められます。
-
-
あなたは高速道路を走るバスを運転しています。バスは興奮しきったやんちゃな生徒でいっぱいであり、みな喉を乾かしています。バスにはソーダのドリンクバーが付いていて、バスに乗っている生徒は一分ごとに 1 オンスのソーダを飲みます。あなたの目標は生徒が飲むソーダの量を最小にしながら生徒を早く送り届けることです。
どのバス停で何人の生徒が降りるかをあなたは把握しています。バスは高速道路の (おそらくは端ではない) どこかから出発し、一定の速度毎時 37.4 マイルで進みます。バスは高速道路だけを使って移動しますが、あるバス停についた後に元来た方向に出発することは許されています (バスを止めて、生徒を下ろして、方向を変えて出発することは瞬時に行えます)。
ソーダの消費量を最小にするように生徒の降ろす効率の良いアルゴリズムを説明してください。入力はバスのルート (バス停の名前とバス停の間の距離) と各バス停で降りる生徒の人数、バスの初期位置 (バス停のうちどれか) からなります。
-
文字列 \(A, B\) の要約 (summary) を、次の形をした部分文字列を結合したものと定義します:
-
\(\color{maroon}{\blacktriangle\texttt{SNA}}\) は最初の文字列 \(A\) にだけ含まれる \(\color{maroon}{\texttt{SNA}}\) という部分文字列を表す。
-
\(\blacklozenge\texttt{FOO}\) は \(A, B\) 両方に含まれる部分文字列 \(\texttt{FOO}\) を表す。
-
\(\color{#0071BB}{\blacktriangledown\texttt{BAR}}\) は二番目の文字列 \(B\) にだけ含まれる \(\color{#0071BB}{\texttt{BAR}}\) という部分文字列を表す。
要約が有効 (valid) であるとは、要約をこのルールに沿って (分割記号を無視しながら) 結合したときに \(A, B\) が復元できることを言います。通常の文字は \(1\) の長さを持ち、分割文字 \({\color{maroon}\blacktriangle}, \blacklozenge, {\color{#0071BB}\blacktriangledown}\) は非負の長さ \(\Delta\) を持つとします。要約の長さは文字と分割記号の長さの和です。例として、\(\color{maroon}{\texttt{KITTEN}}\) と \(\color{#0071BB}{\texttt{KNITTING}}\) の有効な要約とその長さを示します:
-
\(\blacklozenge\texttt{K}{\color{#0071BB}{\blacktriangledown\texttt{N}}}\blacklozenge\texttt{ITT}{\color{maroon}\blacktriangle\texttt{E}}{\color{#0071BB}{\blacktriangledown\texttt{I}}}\blacklozenge\texttt{N}{\color{#0071BB}\blacktriangledown\texttt{G}}\) の長さは \(9 + 7 \Delta\) です。
-
\(\blacklozenge\texttt{K}{\color{#0071BB}\blacktriangledown\texttt{N}}\blacklozenge\texttt{ITT}{\color{maroon}\blacktriangle\texttt{EN}}{\color{#0071BB}\blacktriangledown\texttt{ING}}\) の長さは \(10 + 5 \Delta\) です。
-
\(\blacklozenge\texttt{K}{\color{maroon}\blacktriangle\texttt{ITTEN}}{\color{#0071BB}\blacktriangledown\texttt{NITTING}}\) の長さは \(13 + 3 \Delta\) です。
-
\({\color{maroon}\blacktriangle\texttt{KITTEN}}{\color{#0071BB}\blacktriangledown\texttt{KNITTING}}\) の長さは \(14 + 2 \Delta\) です。
与えられた二つの文字列 \(A[1..m]\) と \(B[1..n]\) の最短の要約の長さを求めるアルゴリズムを説明、解析してください。入力には \(\Delta\) の長さも含まれます。例えば:
-
\(\color{maroon}{\texttt{KITTEN}}\) と \(\color{#0071BB}{\texttt{KNITTING}}\) と \(\Delta = 0\) が入力のとき、答えは \(9\) です。
-
\(\color{maroon}{\texttt{KITTEN}}\) と \(\color{#0071BB}{\texttt{KNITTING}}\) と \(\Delta = 1\) が入力のとき、答えは \(15\) です。
-
\(\color{maroon}{\texttt{KITTEN}}\) と \(\color{#0071BB}{\texttt{KNITTING}}\) と \(\Delta = 2\) が入力のとき、答えは \(18\) です。
-
-
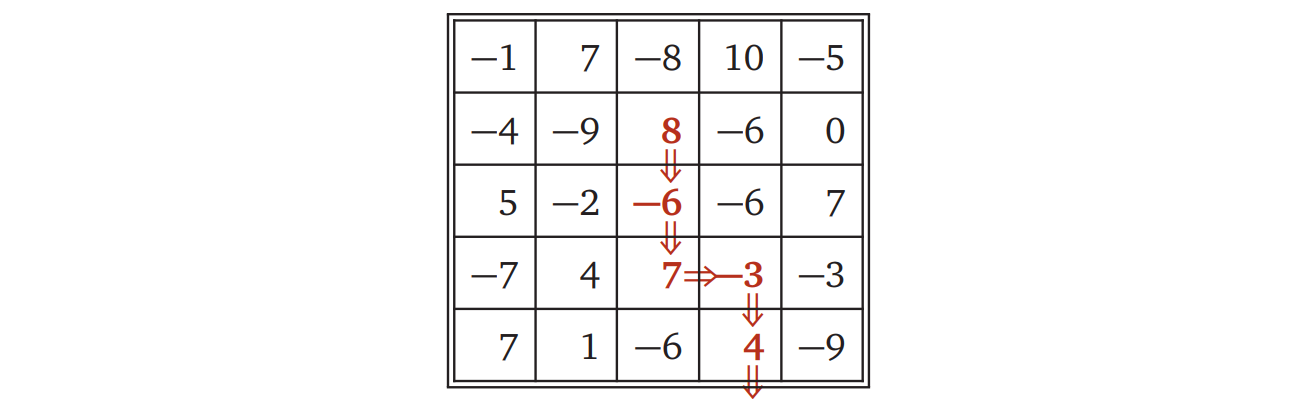
Vankin's Mile は \(n \times n\) の格子状の盤を使って遊ぶ一人用ゲームです。プレイヤーは好きなところに駒を置いてからゲームを始め、ターンごとに駒を右または下に動かし、駒が盤の端についたらゲーム終了です。盤のマスには実数が書かれていて、プレイヤーのスコアはゲームが終わるまでに通ったマスに書かれている数字の和です。ゲームの目標はなるべく多くのポイントを集めることです。
例えば次の盤が与えられたとき、二行目の \(8\) からゲームを始めて下、下、右、下、下と進むことで \(8 - 6 + 7 - 3\)\({} + 4 = 10\) 点を獲得できます (この点数はこの盤に対する最高得点ではありません)。
-
盤を表す \(n \times n\) の二次元配列が与えられたときに、Vankin's Mile で獲得できる最高得点を計算する効率の良いアルゴリズムを説明、解析してください。
-
このゲームのヨーロッパ版は Vankin's Kilometer というヨーロッパらしい名前をしています。このゲームはルールが少し違っていて、プレイヤーは右、下だけでなく左にも移動できます。ただし無限ループを避けるために一度通ったマスは以降通れないものとします。盤を表す \(n \times n\) の二次元配列が与えられたときに、Vankin's Kilometer で獲得できる最高得点を計算する効率の良いアルゴリズムを説明、解析してください21。
-
-
要素が \(0\) と \(1\) からなる \(n \times n\) のビットマップ \(M[1..n, 1..n]\) が与えられたとします。\(M[i..i^{\prime}, j..j^{\prime}]\) という形をした部分が全て同じ要素を持っているとき、それを \(M\) の一様区画 (solid block) と言います。一様区画の行の数と列の数が等しいとき、正方 (square) であると言います。
-
\(M\) に含まれる最大の正方一様区画の大きさを \(O(n^{2})\) 時間で求めるアルゴリズムを説明してください。
-
\(M\) に含まれる最大の一様区画の大きさを \(O(n^{3})\) 時間で求めるアルゴリズムを説明してください。
-
\(M\) に含まれる最大の一様区画の大きさを \(O(n^{2} \log n)\) 時間で求めるアルゴリズムを説明してください。 [ヒント: 分割統治]
-
❤ \(M\) に含まれる最大の一様区画の大きさを \(O(n^{2})\) 時間で求めるアルゴリズムを説明してください。
-
-
\(M[1..n, 1..n]\) の形をした実数配列が与えられたときに、長方形の部分列 \(M[i..i^{\prime}, j..j^{\prime}]\) で要素の和が最大のものを求めるアルゴリズムを説明してください。満点のためには実行時間が \(O(n^{3})\) であることが求められます。 [ヒント: 練習問題 3.2]
-
与えられたビットマップに二回以上出現する最大の長方形パターンを見つけるアルゴリズムを説明、解析してください。つまり二次元配列 \(M[1..n, 1..n]\) が与えられたときに、\(M\) に繰り返し現れる最大の長方形パターンの面積を計算してください。例えば次の図の左に示すビットマップが入力されたとき、条件を満たす最大の長方形パターンは 15 \(\times\) 13 のワン公なので、アルゴリズムの出力は 195 です (この例では二つのパターンは重なっていませんが、重なっていても構いません)。

-
満点のためには、\(O(n^{5})\) 時間で実行されるアルゴリズムを説明してください。
-
❤ ボーナス点のためには、\(O(n^{4})\) 時間で実行されるアルゴリズムを説明してください。
-
♣ ❤ さらなるボーナス点のためには、\(O(n^{3} \text{ polylog } n)\) 時間で実行されるアルゴリズムを説明してください。
-
-
\(P\) を平面上の凸 (convex) な点集合とします。直感的に言うと、\(P\) に含まれる点の周りに輪ゴムを張ると全ての点が輪ゴムと接します。きちんと言うと、 任意の \(p \in P\) について \(p\) と他の全ての点を分ける直線が存在します。この点集合に対して、 一番左にある点 \(P[1]\) から始めて "輪ゴム" を反時計回りにたどることで \(P[1], P[2], \ldots, P[n]\) と名前を付けます。
この問題で解くのは巡回セールスマン問題の特別の場合です。つまりセールスマンは通常通り \(P\) の全ての点を訪れますが、\(p \in P\) から \(q \in P\) に移動するに移動するときのコストはユークリッド距離 \(|pq|\) とします。
-
\(P\) の最短の環状な周遊 (tour)を求める単純なアルゴリズムを説明してください。
-
周遊が単純 (simple) であるとは自分自身と交差しないことを言います。今考えている \(P\) の最短の周遊は単純でなければならないことを証明してください。
-
左端の点 \(P[1]\) から始まって右端の点 \(P[r]\) で終わる最短の周遊を計算する効率の良いアルゴリズムを説明、解析してください。
-
終点に制限のない \(P\) の最短の周遊を計算する効率の良いアルゴリズムを説明、解析してください。
-
-
❤ 巡回セールスマン問題を \(O(2^{n} \text{poly}(n))\) 時間で解くアルゴリズムを説明、解析してください。アルゴリズムには辺に重みの付いた \(n\) 頂点の無向グラフ \(G\) が与えられ、アルゴリズムが返すのは全ての頂点をちょうど一回ずつ通る一番軽い巡回路の重さ、あるいはそのような巡回路が存在しない場合には \(\infty\) です。 [ヒント: バックトラッキングを使った自明な再帰的アルゴリズムの実行時間は \(O(n!)\) です。]
-
\(W=\lbrace w_{1}, w_{2}, \ldots, w_{n} \rbrace\) を固定されたアルファベット \(\Sigma\) に対する文字列の有限集合とします。 \(W\) の編集中心 (edit center) とは文字列 \(C \in \Sigma^{\ast}\) であって \(W\) に属する文字列との編集距離の最大値が最小になるものを言います。編集半径 (edit radius) とは編集中心と \(W\) に属する文字列との編集距離の最大値のことです。文字列の集合は複数の編集中心を持つことがありますが、編集半径は一つしか持ちません。 \[ \begin{aligned} \mathit{EditRadius}(W) & := \min\limits_{C \in \Sigma^{\ast}} \max\limits_{w \in W} \mathit{Edit}(w, C) \\ \mathit{EditCenter}(W) & := \underset{C \in \Sigma^{\ast}}{\textrm{\footnotesize argmin}} \max\limits_{w \in W} \mathit{Edit}(w, C) \end{aligned} \]
-
与えられた三つの文字列の編集中心を計算するアルゴリズムを説明、解析してください。
-
♣ ❤ 任意の文字列集合の編集半径を最悪でも真の値から \(2\) 倍の範囲で近似する効率の良いアルゴリズムを説明、解析してください (文字列の数が固定されていない場合、編集距離の真の値を求めるのは NP 困難です)。
-
-
❤ \(0\) から \(9\) の一桁の整数からなる配列 \(D[1..n]\) について、\(D\) のデジタル部分列 (digital subsequence) とは \(D\) の互いに重ならない部分文字列を元の配列と同じ順番に並べたものを、通常の数字の列として読んだときの列です。例えば 3, 4, 5, 6, 8, 9, 32, 38, 46, 64, 83 は、円周率の最初の部分の数列としたときのデジタル部分配列です: \[ |3|, 1, |4|, 1, |5|, 9, 2, |6|, 5, 3, 5, |8|, |9|, 7, 9, |3, 2|, |3, 8|, |4, 6|, 2, |6, 4|, 3, 3, |8, 3| \]
デジタル部分配列の長さを含まれる数字の数として定義します (含まれる数字の桁数の和ではありません)。この例では長さは 12 です。通常の配列と同じように、全ての数が一つ前の数よりも大きい場合デジタル部分配列を増加 (increasing) であると言うことにします。
\(D\) の最長増加デジタル部分配列を計算する効率の良いアルゴリズムを説明、解析してください。 [ヒント: 計算量に関する仮定に注意! \(k\) 桁の数の比較演算の実行時間はいくつですか?]
満点のためには、アルゴリズムの実行時間が \(O(n^{4})\) であることが求められます。これよりも速いアルゴリズムにはボーナス点が付きます。私が知っている範囲で最速のアルゴリズムの実行時間は \(O(n^{3 / 2} \log n)\) です。この実行時間を達成するにはアルゴリズムの設計と解析にいくつかのトリックが必要ですが、全てこの講義の範囲に収まっています 22。
-
❤ 古典的な Hanoi の塔問題を次のように改変したものを考えます。通常の問題と同じように \(n\) 枚の異なる大きさの円盤と \(0, 1, 2\) と番号のついた \(3\) つの杭があり、最初 \(n\) 枚の円盤は全て杭 \(0\) に置かれ、大きいものが一番下で、上に行くほど小さくなるようになっています。目標は全ての円盤を杭 \(2\) に移動させることです。行うことができる操作はある杭の一番上に載っている円盤一つを別の杭に移動させることだけであり、この操作には従わなければならないルールがあります。まず、円盤をそれよりも小さな円盤の上に置くことはできません。次に、これが標準の問題との唯一の違いなのですが、杭 \(0\) から杭 \(2\) に円盤を直接移動させることはできません。
このルールの下で、\(n\) 枚の円盤全てを杭 \(0\) から杭 \(2\) に移動させるための最小の操作数を求めるアルゴリズムを説明、解析してください。満点を得るためには、最悪ケースでも \(O(\log n)\) 回の算術演算を使うことが求められます。解析のときには、\(k\) 桁の数の加算と乗算命令の実行時間が \(O(k)\) であるとしてください。 [ヒント: 行列!]
\({}\)
列/配列の分割
-
基本算術式 (basic arithmetic expression) は \(\lbrace 1, +, \times \rbrace\) と括弧から構成されます。ほぼ全ての整数について、その数を表す基本算術式は複数あります。 例えば次の基本算術式は全て 14 を表します: \[ \begin{gathered} 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 \\ ((1 + 1) × (1 + 1 + 1 + 1 + 1)) + ((1 + 1) × (1 + 1)) \\ (1 + 1) × (1 + 1 + 1 + 1 + 1 + 1 + 1) \\ (1 + 1) × (((1 + 1 + 1) × (1 + 1)) + 1) \end{gathered} \]
\(n\) が与えられたときに、\(n\) を基本算術式で表すために必要になる \(1\) の数の最小値を求めるアルゴリズムを説明、解析してください。括弧の数は関係なく、1 の数だけを考えます。先ほどの \(n = 14\) の例では、最後の基本算術式に対応する \(8\) が答えです。アルゴリズムの実行時間は次数の小さい多項式で抑えられるはずです。
-
\(+\) と \(-\) で区切られた整数列を与えられたとします。例えば次のような列です: \[ \begin{gathered} 1 + 3 - 2 - 5 + 1 - 6 + 7 \end{gathered} \] これを式とみなした上で括弧を付けると、式が表す値が変化します: \[ \begin{gathered} 1 + 3 - 2 - 5 + 1 - 6 + 7 = -1 \\ (1 + 3 - (2 - 5)) + (1 - 6) + 7 = 9 \\ (1 + (3 - 2)) - (5 + 1) - (6 + 7) = -17 \end{gathered} \]
\(+\) と \(-\) で区切られた整数列を受け取って、それを式とみなしたときに括弧を付けることで表すことができる値の最大値を求めるアルゴリズムを説明、解析してください。括弧は加算と減算をまとめるために使うことだけが許されています。 \(1 + 3(-2)(-5) + 1 - 6 + 7 = 33\) のように括弧を続けて書いて乗算を表すことはできません。
-
\(+\) と \(\times\) で区切られた整数列を与えられたとします。例えば次のような列です: \[ 1 + 3 \times 2 \times 0 + 1 \times 6 + 7 \] これを式とみなした上で括弧を付けると、式が表す値が変化します: \[ \begin{gathered} (1 + (3 \times 2)) \times 0 + (1 \times 6) + 7 = 13 \\ ((1 + (3 \times 2 \times 0) + 1) \times 6) + 7 = 19 \\ (1 + 3) \times 2 \times (0 + 1) \times (6 + 7) = 104 \end{gathered} \]
-
入力の整数が全て正だと仮定したときに、括弧を付けることで表すことができる値の最大値を求めるアルゴリズムを説明、解析してください。 [ヒント: この問題は簡単です。]
-
入力の整数が全て非負だと仮定したときに、括弧を付けることで表すことができる値の最大値を求めるアルゴリズムを説明、解析してください。
-
入力の整数に制約がない場合に、括弧を付けることで表すことができる値の最大値を求めるアルゴリズムを説明、解析してください。
算術演算は \(O(1)\) で実行できるとしてください。
-
-
あなたは Shampoo-Banana 大学を卒業し、ウォールストリートの Long Live Boole 銀行の就職面接を受けることに決めました。銀行のマネージャー Eloob Egroeg は新入りの従業員に対して制限時間が 24 時間の "解答か死か" 形式の問題を出して、この問題が解けなければその時点で首を切ると言います!
あなたが銀行に初めて入ると、従業員のオフィスは一列に並んでいて、それぞれのドアには "\(T\)" あるいは "\(F\)" と大きく印が付いていました。さらに隣り合うオフィスの間には \(\land, \lor, \oplus\) の記号のどれか一つが書かれたボードがあります。この難解な記号について Eloob に尋ねたところ、\(T, F\) はブール値 \(\textsc{True}\) と \(\textsc{False}\) を表し、ボードに書いてある記号はブール演算の \(\textsc{And}, \textsc{Or}, \textsc{Xor}\) を表すと教えてくれました。また文字と記号は特定の従業員の組み合わせが一緒に上手く働けるかどうかを表しているとのことです。新しいプロジェクトを始めるとき、 Eloob は記号列の間に括弧を入れて曖昧性の無いブール式にすることで従業員をグループに分け、括弧を入れたブール式が \(T\) に評価されるならばそのプロジェクトは成功するそうです。
例えば銀行に三人の従業員がいて、オフィスのドアとオフィスの間のボードに書かれている記号が \(T \land F \oplus T\) だとすると、括弧をつけて全体を \(T\) にする方法は \((T \land (F \oplus T))\) の一つです。しかし記号列が \(F \land T \oplus F\) だった場合、どう括弧を入れてもプロジェクトは失敗します。
そして Eloob が出した "解答か死か" の面接問題はこれです: 与えられた記号列に括弧を入れることで全体の式が \(T\) に評価されるようにできるかどうかを判定するアルゴリズムを説明してください。アルゴリズムの入力は配列 \(S[0..2n]\) であり、\(i\) が偶数のとき \(S[i] \in \lbrace T, F \rbrace\) 、\(i\) が奇数のとき \(S[i] \in \lbrace \land, \lor, \oplus \rbrace\) です。
-
南極カタツムリ同好会 Upper Glacierville 支部 (Antarctican Snail Lovers of Upper Glacierville) は毎年の会合で "円卓の友レース" を開催しています。 \(1\) から \(n\) までの番号がつけられた育ちの良いカタツムリが円卓の端に置かれた状態からスタートし、合図と共にねばねばした跡を残しながら卓上を動き回ります。カタツムリたちは自分と他のカタツムリの残した跡を横切らないように訓練されており、卓から落ちることもありません。二匹のカタツムリが出会うとそのカタツムリのペアは繁殖の準備ができたとみなされ、卓から取り除かれて子供を作るためのロマンチックな部屋に放り込まれます。このレースでは制限時間がなかったとしても相手を見つけられないカタツムリが出る場合があることに注意してください。
![レースの終了の一例を図示したもの。カタツムリ 6 と 8 は相手を見つけられない。主催者は \(M[3,4] + M[2,5] + M[1,7]\) を払う。](/algorithms/AlgorithmFigure_3-6.png) 図 3.6レースの終了の一例を図示したもの。カタツムリ 6 と 8 は相手を見つけられない。主催者は \(M[3,4] + M[2,5] + M[1,7]\) を払う。
図 3.6レースの終了の一例を図示したもの。カタツムリ 6 と 8 は相手を見つけられない。主催者は \(M[3,4] + M[2,5] + M[1,7]\) を払う。円卓の友レース中に成立した全てのカタツムリのカップルに対して、Antarctican SLUG のレース主催者は祝い金を支払います。二次元配列 \(M[1..n, 1..n]\) が円卓の後ろの壁に貼られており、カタツムリ \(i\) と \(j\) が出会ったときには \(M[i,j] = M[j,i]\) が双方のカタツムリの飼い主に支払われます。
入力として \(M\) が与えられたときに、主催者が払う必要が生じうる最高金額を計算するアルゴリズムを説明、解析してください。
-
あなたは採石場から大理石の大きな板を採掘しました。簡単のため、大理石の板は横 \(n\) インチ、縦 \(m\) インチの長方形だとします。キッチンカウンター、彫刻、墓石などで使うために、この大理石から様々な形の小さな長方形を切り出したいとします。
あなたは任意の大きさの長方形の大理石を水平あるいは垂直にカットできる大理石カッターを持っています。また横 \(x\) インチ、縦 \(y\) インチの大理石の板の値段を表す配列 \(P[x, y]\) があり、いつでも参照できます。この値段は客の需要によって決まっていますが、キッチンカウンターで使う大理石を買いに来るお客というのは少し変わっているので、彼らについて常識的な仮定を置かないでください。つまり、大きい板が小さい板よりも極端に低い値段で売れることもあります。
横 \(x\) インチ、縦 \(y\) インチの板の値段を表す配列と板のサイズ \(m, n\) を入力として受け取って、売り上げを最大化する \(m \times n\) インチの板の分割方法を計算するアルゴリズムを説明してください。
-
この問題では特定の制約を満たす最適二分探索木を構築する効率の良いアルゴリズムを設計してもらいます。入力はソート済みの鍵配列 \(A[1..n]\) と頻度数配列 \(f[1..n]\) であり、\(f[i]\) が \(A[i]\) に対する探索の回数を表します。問題は基本的に以前に示したものと同じですが、ここでは追加の制約があります。
-
AVL 木 (AVL tree) は自動的にバランスが保たれる二分探索木のうち最初に発見されたものであり、1962 年に Georgy Adelson-Velsky (ゲオルギー・アデルソン・ヴェルスキー) と Evgenii Landis (エフゲニー・ランディス) によって提案されました。AVL 木では任意の頂点 \(v\) について、\(v\) の左右の部分木の高さは最大でも \(1\) しか違いません。
鍵と頻度を表す配列を受け取って最適な AVL 木を返すアルゴリズムを説明、解析してください。
-
対称二分 B 木 (symmetric binary B-tree) も自動的にバランスが保たれる二分木であり、1972 年にRudolf Bayer (ルドルフ・ベイヤー) によって提案されました。1978 年に Robert Sedgewick (ロバート・セッジウィック) と Leonidas Guibas (レオニダス・ギバス) によって単純な形に変形され、現在では赤黒木 (red-black tree)という名前で知られています。
赤黒木は次の制約を持つ二分探索木です:
- 全ての頂点は赤または黒である。
- 赤い頂点の親は黒い。
- 根から葉への任意の道は同じ数の黒い頂点を含む。
鍵と頻度を表す配列を受け取って最適な赤黒木を返すアルゴリズムを説明、解析してください。
-
AA 木 (AA tree) は 1993 年に Arne Andersson (アルネ・アンデルソン) によって提案され、2000 年に Mark Allen Weiss (マーク・アレン・ウェイス) によって単純化され (そして名前を付けられ) ました。2006 年には Robert Sedgewick によって鏡写しの (バランスを保つためのアルゴリズムが異なる) データ構造が提案されていますが、このデータ構造は "AA 木" ではなく "左に傾いた赤黒木" と呼ばれました。
AA 木は次の追加の制約を持つ赤黒木です:
- 左の子は赤くない23。
鍵と頻度を表す配列を受け取って最適な AA 木を返すアルゴリズムを説明、解析してください。
-
-
\(0\) と \(1\) からなる \(n \times n\) のビットマップ \(M[1..n, 1..n]\) が与えられたとします。\(M[i..i^{\prime}, j..j^{\prime}]\) という形をした部分が全て同じ要素を持っているとき、それを \(M\) の一様区画 (solid block) と言います。\(M\) をなるべく少ない数の互いに重ならない一様区画に分割したいとします。
この問題に対する単純な再帰的戦略の一つに、ギロチン分割と呼ばれるものがあります。ギロチン分割は \(M\) が一様区画であれば何もせず、そうでなければ水平または垂直に \(M\) を分割して両方の部分を再帰的に一様区画に分割するというものです。
任意のギロチン分割は二分木で表せます。この二分木の頂点は分割の場所と方向を保持し、葉は対応する一様区画の要素 \(0\) または \(1\) を保持します。ギロチン分割のサイズとは対応する二分木の葉の数 (つまり、最終的に残る一様区画の数) であり、ギロチン分割の深さとは対応する二分木の深さです。
-
\(M\) のギロチン分割でサイズが最小なものを計算するアルゴリズムを説明、解析してください。
-
ギロチン分割を使った分割をしても常に一様区画の数が最小になるわけではないことを示してください。
-
\(M\) のギロチン分割で深さが最小なものを計算するアルゴリズムを説明、解析してください。
-
\(M\) のギロチン分割を表す二分木と添え字 \(i, j\) から \(M[i,j]\) を計算するアルゴリズムを説明、解析してください。
-
ギロチン分割におけるピクセル \(M[i,j]\) の深さを、ギロチン分割を表す二分木におけるそのピクセルが含まれる葉の深さとして定義します。 \(M\) のギロチン分割でピクセルの深さの和が最小なものを計算するアルゴリズムを説明、解析してください。
-
\(M\) のギロチン分割で黒いピクセルの深さの和が最小なものを計算するアルゴリズムを説明、解析してください。
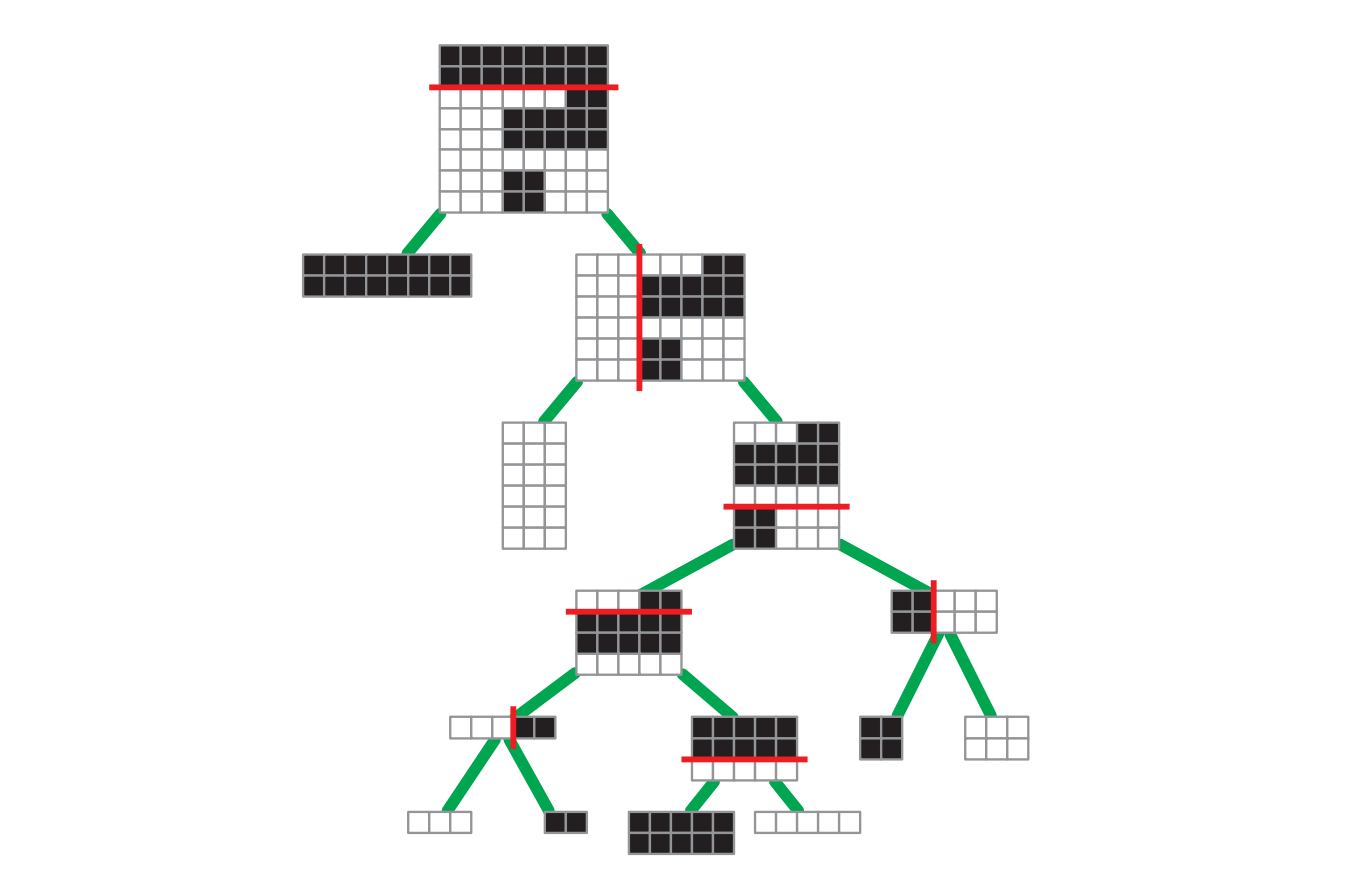 図 3.7サイズ \(8\)、深さ \(5\) のギロチン分割
図 3.7サイズ \(8\)、深さ \(5\) のギロチン分割 -
-
♠ おめでとうございます!あなたは巨大オンライン書店 DeNile ("Not just a river in Egypt!") に雇われ、倉庫ロボットを最適化する仕事をすることになりました。DeNile が販売する全ての本には ISBN (Internatinal Standard Book Number) というユニークな数字が付いています。DeNile の倉庫には箱が一列に並んでおり、それぞれの箱には一種類の本が何冊か入っています。この箱は ISBN によってソートされており、ISBN は箱の表面に機械が読める形式で書かれています。書店が注文を受けると、箱の列に沿って移動できるロボットが本を取りに行きます。
DeNile にはどの箱にどの ISBN が入っているかのリストを持っていません (問題が簡単になりすぎます!)。その代わり、ロボットは本を取りに行くたびに二分探索を行います。探索にはロボットの物理的な動作が関わるために、探索の各ステップが \(O(1)\) 時間で終わるという仮定は成り立たなくなります。つまり:
-
ロボットは常に 0 番目の箱から探索を始める (配送用の箱がここにある)。
-
\(i\) 番目の箱から \(j\) 番目の箱に移動するには \(\alpha |i - j|\) 秒かかる ( \(\alpha\) は定数)。
-
箱の ISBN を読み取るためには箱の真正面にいなければならない。ISBN の読み取りには \(\beta\) 秒かかる ( \(\beta\) は定数 )。
-
ロボットの方向を変えるには \(\gamma\) 秒かかる ( \(\gamma\) は定数 )。
-
ロボットが目的の箱を見つけたら、箱から本を取り出して 0 番目の箱の場所に戻る。
ロボットによる箱の探索を最短にする二分探索木を計算するアルゴリズムを説明、解析してください。アルゴリズムの入力は整数配列 \(f[1..n]\) であり、\(f[i]\) が \(i\) 番目の箱にある本を取りに行く回数を表します。 \(\alpha, \beta, \gamma\) も入力として与えられます。
-
-
♠ 探索木のキャッシュパフォーマンスを向上させるためによく使われる方法の一つに、鍵と部分木を通常よりも多く頂点に格納するというものがあります。B-木 (B-tree) とは、葉でない頂点が最大 \(B\) 個の鍵と最大 \(B+1\) 個のより小さい B-木 (子) へのポインタを格納している根付き木です。具体的に言うと、B-木の頂点 \(v\) は三つのフィールドを持ちます:
- 正の整数 \(\mathit{v.d} \leq B\)
- ソート済みの配列 \(\mathit{v.key}[1..v.d]\)
- 子へのポインタの配列 \(\mathit{v.child}[0..v.d]\)
この制約は頂点の子の数が鍵の数よりちょうど一つ多くなることを表しています24。
ポインタ \(\mathit{v.child}[i]\) は \(\textsc{Null}\) または他の B-木の根へのポインタです。 \(\mathit{v.child}[i]\) が木の根を指す場合、その木は \(\mathit{v.key}[i]\) より大きく \(\mathit{v.key}[i+1]\) よりも小さい鍵を保持します。また左端の部分木 \(\mathit{v.child}[0]\) は \(\mathit{v.key}[1]\) よりも小さい鍵を、右端の部分木 \(\mathit{v.child}[v.d]\) は \(\mathit{v.key}[v.d]\) よりも大きい鍵をそれぞれ保持します。
直感的には、次のような図を思い浮かべることができるはずです:
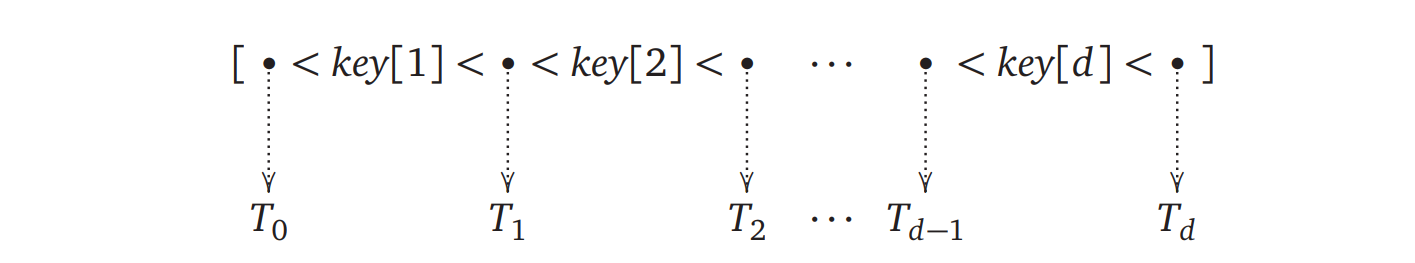
図中の \(T_{i}\) は \(\mathit{child}[i]\) によって指される部分木です。
B-木の鍵 \(x\) に対する探索コストとは根から \(x\) を含む頂点への道の長さです。また 1-木は二分探索木です。
整数 \(B > 0\) を固定します (実際のコードでは \(B = 8\) が推奨されます)。ソート済みの鍵配列 \(A[1..n]\) と頻度を表す配列 \(F[1..n]\) が与えられ、\(F[i]\) が \(A[i]\) の探索される回数を表すとします。この問題の目標は合計探索時間が最小となる B-木を構築する効率の良いアルゴリズムを説明、解析することです。
-
特殊ケース \(B=2\) に対する多項式時間アルゴリズムを説明してください。
-
任意の \(B\) に対して、実行時間が整数定数 \(c\) を使って \(O(n^{B+c})\) と表されるアルゴリズムを説明してください。
-
❤ 任意の \(B\) に対して、実行時間が整数定数 \(c\) を使って \(O(n^{c})\) と表される (\(\pmb{B}\) に依存しない) アルゴリズムを説明してください。
-
丸括弧 \(\color{green}{()}\) と鍵括弧 \(\color{#B52F1B}{[]}\) からなる文字列 \(w\) のバランスが取れている (balanced) とは、次の条件のうちどれかを満たすことを言います:
- \(w\) は空文字列である。
- バランスの取れた文字列 \(x\) を使って \(w = {\color{green}{(}} x {\color{green}{)}}\) と表せる。
- バランスの取れた文字列 \(x\) を使って \(w = {\color{#B52F1B}{[}} x {\color{#B52F1B}{]}}\) と表せる。
- バランスの取れた文字列 \(x,y\) を使って \(w = xy\) と表せる。
例えば \[ w = {\color{green}{(}} {\color{#B52F1B}{[}} {\color{green}{(}} {\color{green}{)}} {\color{#B52F1B}{]}} {\color{#B52F1B}{[}} {\color{#B52F1B}{]}} {\color{green}{(}} {\color{green}{)}} {\color{green}{)}} {\color{#B52F1B}{[}} {\color{green}{(}} {\color{green}{)}} {\color{green}{(}} {\color{green}{)}} {\color{#B52F1B}{]}} {\color{green}{(}} {\color{green}{)}} \] はバランスの取れた文字列です。なぜなら次のように \(x,y\) を定義すると \(w = xy\) であり、 \(x\) と \(y\) がバランスの取れた文字列だからです: \[ x = {\color{green}{(}} {\color{#B52F1B}{[}} {\color{green}{(}} {\color{green}{)}} {\color{#B52F1B}{]}} {\color{#B52F1B}{[}} {\color{#B52F1B}{]}} {\color{green}{(}} {\color{green}{)}} {\color{green}{)}}, \quad y = {\color{#B52F1B}{[}} {\color{green}{(}} {\color{green}{)}} {\color{green}{(}} {\color{green}{)}} {\color{#B52F1B}{]}} {\color{green}{(}} {\color{green}{)}} \]
-
入力として丸括弧と鍵括弧からなる文字列が与えられます。この文字列のバランスがとれているかどうかを判定するアルゴリズムを説明、解析してください。
-
入力として丸括弧と鍵括弧からなる文字列が与えられます。この文字列のバランスがとれている部分列で最長のものの長さを計算するアルゴリズムを説明、解析してください。
-
入力として丸括弧と鍵括弧からなる文字列が与えられます。この文字列のバランスがとれている超配列で最短のものの長さを計算するアルゴリズムを説明、解析してください。
-
入力として丸括弧と鍵括弧からなる文字列が与えられます。丸括弧と鍵括弧のバランスがとれている文字列とこの文字列との間の編集距離の最小値を計算するアルゴリズムを説明、解析してください。
-
❤ 入力として丸括弧と鍵括弧からなる二つの文字列が与えられます。二つの文字列のバランスの取れた最長共通部分列を計算するアルゴリズムを説明、解析してください。
-
❤ 入力として丸括弧と鍵括弧からなる文字列が与えられます。この文字列のバランスが取れていてかつ回文である部分列で最長のものを計算するアルゴリズムを説明、解析してください。
-
❤ 入力として丸括弧と鍵括弧からなる二つ文字列が与えられます。二つの文字列のバランスが取れていてかつ回文である共通部分列で最長のもの (!!!) を計算するアルゴリズムを説明、解析してください。
いずれの問題でも、入力は \(w[1..n]\) \((w[i] \in \lbrace {\color{green}{(}}, {\color{green}{)}}, {\color{#B52F1B}[}, {\color{#B52F1B}]} \rbrace)\) です。
-
おめでとうございます!あなたは DARPA, Google, McDonald が出資する 5000 万ドルのプロジェクトを勝ち取りました。このプロジェクトでは、プログラマーの脳を読む世界初のコンパイラ DWIM を作成します!研究提案書と数えきれないプレスリリースで、あなたは DWIM が任意のコード片に含まれるエラーを自動的に修正し、そのときのコードの改変は最小限であると宣伝してきました。そして残念なことに、このブツを実際に作る時間がついにやってきました。
あなたはウォーミングアップとして、次の小さな問題に取り組むことにしました。二つの文字列の間の編集距離とは、一文字の挿入、削除、置換を使って片方の文字列をもう片方の文字列に変形するときに必要になる操作の回数の最小値であることを思い出してください。また \(w\) が算術式であるとは、次の条件を満たすことを言います:
- \(w\) が一つ以上の数字の桁からなる文字列である。
- 算術式 \(x\) を使って \(w = (x)\) と表せる。
- 算術式 \(x, y\) と二項演算子 \(\diamond\) を使って \(w = x \diamond y\) と表せる。
アルファベット \(\lbrace \#, \diamond, (, ) \rbrace\) (\(\#\) は一桁の数、\(\diamond\) は二項演算子 ) からなる文字列が与えられたときに、その文字列から算術式への編集距離の最小値を求めるアルゴリズムを説明、解析してください。
-
リボ核酸 (RNA) 分子はヌクレオチド (基) が数百万個つながった長い鎖であり、基にはアデニン (\(A\))、シトシン (\(C\))、グアニン (\(G\))、ウラシル (\(U\)) の四種類があります。RNA 分子の配列は文字列 \(b[1..n]\) で表され、各 \(b[i] \in \lbrace A, C, G, U \rbrace\) が基に対応します。鎖上で隣り合う分子同士の化学結合に加えて、ある条件を満たす基の間には水素結合が作られます。水素結合で結合した基の組とRNA 配列の全体を指して RNA 分子の二次構造と言います。
二つの基の組 \((i, j)\) と \((i^{\prime}, j^{\prime})\) (\(i < j\) かつ \(i^\prime < j^{\prime}\)) が重なるとは、\(i < i^{\prime} < j < j^{\prime}\) または \(i^{\prime} < i < j^{\prime} < j\) が成り立つことを言います。現実の二次構造はほとんどの組は重なっていません。重なる基の組は二次構造でいわゆる pseudoknots を形成しますが、これは予測が困難です。
与えられた RNA 配列に対する最良の二次構造を予測したいとします。二次構造のモデルとして、次の大胆に単純化したモデルを使います:
- 基は多くとも一つの他の基と結合する。
- A-U と C-G の組だけが結合できる。
- \((i, i+1)\) と \((i, i + 2)\) という形の基は結合できない。
- 結合する基の組同士は重なってはいけない。
最後の (全く現実的でない) 制限があるので、RNA の二次構造を太った木 (fat tree) に近いものを使って可視化できます:
 図 3.8. RNA の二次構造の例。赤線で示された 21 個の結合ペアを持つ。ギャップは破線で囲まれている。この構造のスコアは \(2^{2} + 2^{2} + 8^{2} + 1^{2} + 7^{2} + 4^{2} + 7^{2} = 187\) である。
図 3.8. RNA の二次構造の例。赤線で示された 21 個の結合ペアを持つ。ギャップは破線で囲まれている。この構造のスコアは \(2^{2} + 2^{2} + 8^{2} + 1^{2} + 7^{2} + 4^{2} + 7^{2} = 187\) である。-
与えられた RNA 配列が構成できる結合組の数の最大値を求めるアルゴリズムを説明、解析してください。
-
二次構造におけるギャップ (gap) とは組になっていない極大の部分文字列のことを言います。大きなギャップは科学的に不安定なので、小さなギャップを持つ構造が多く出現します。この傾向を取り入れるために、二次構造のスコアをギャップの長さの二乗和として定義します。例としては上図を見てください (このスコア関数は全く人工的なものです。現実の RNA 構造予測にはこれよりずっと複雑なスコア関数が必要になります)。
RNA 配列が与えられたときに、二次構造の最小スコアを計算するアルゴリズムを説明、解析してください。
-
♣ 正規表現の演算は \(\cdot\) (連結)、\(+\) (和集合)、\({}^{\ast}\) (Kleene 閉包) の三つとします。
-
文字列 \(w\) と正規表現 \(R\) が与えられたときに、\(w \in L(R)\) かどうかを判定する効率の良いアルゴリズムを説明、解析してください。
-
一般化された正規表現 (generalized regular expression) とは普通の正規表現に二項演算子 \(\cap\) (共通部分) と単項演算子 \(\lnot\) (補集合) を加えたものです。一般化された正規表現に対応する NFA が構築できることと Kleene の定理から、一般化された正規表現 \(E\) が表す言語 \(L(E)\) が正規であることが言えます。
文字列 \(w\) と一般化された正規表現 \(E\) が与えられたときに、\(w \in L(E)\) かどうかを判定する効率の良いアルゴリズムを説明、解析してください。
\({}\)
木と部分木
-
-
あなたは Abugida の子会社 Giggle, Inc で行われる初めてのホリデーパーティ (強制参加) の幹事となりました。Giggle の従業員の間には社長を根とした木で表される厳格な上下関係があり、人事部にある全能のオラクルは全ての従業員の "面白さ" を知っています。
パーティが社交的になるように、ある従業員がパーティに出席できるのはその直属の上司がパーティに参加するときだけと決まっています。ただし、社長は面白さの評価が負にもかかわらずパーティに必ず参加します (結局、この会社は彼女のものですから)。面白さの評価の和を最大化する出席者のリストを作成するアルゴリズムを示してください。
-
昨年のホリデーパーティの参加者があまりにも少なかったことから、Giggle の社長は今年はパーティの代わりに全ての従業員にプレゼントを渡すことを決めました。具体的には、従業員は次の三つのうち一つを受け取れます: (1) 世界の好きなところで過ごせる六週間の無料休暇 (2) Jumping Jack Flash's Flapjack Stack Shack の朝食パンケーキ食べ放題券ペア (3) 犬の糞が詰まった燃え盛る紙袋。
直属の上司と同じプレゼントを受け取ることはできないことが社則で決まっています。また直属の上司よりも上等なプレゼントを受け取った従業員は、嫉妬した上司によって首を切られてしまうでしょう。
Giggle の公式パーティを統べる者として、どの従業員がどのプレゼントを受け取るかを決めるのはあなたの仕事です。解雇される従業員の数が最小となるようにプレゼントを配るアルゴリズムを説明してください。ええ、社長に燃え盛る犬の糞を送り付けることもできます。
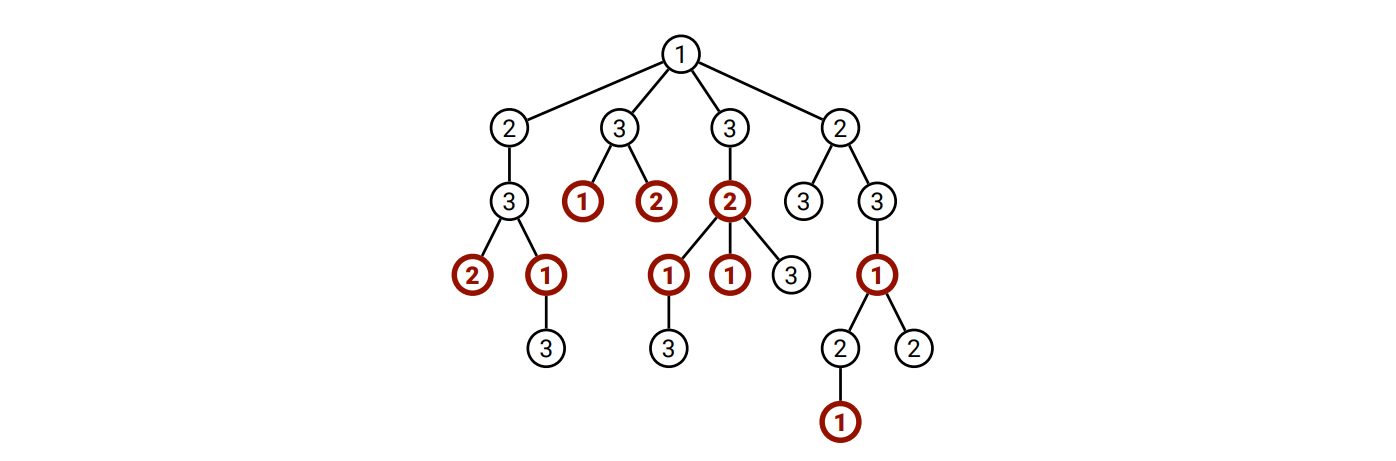 図 3.9コストが \(9\) の割り当て。赤い頂点が親よりも小さい値を割り当てられた頂点を表す。これはこの木に対する最適な割り当てではない。
図 3.9コストが \(9\) の割り当て。赤い頂点が親よりも小さい値を割り当てられた頂点を表す。これはこの木に対する最適な割り当てではない。きちんと問題を定義すると、会社の上下関係を表す根付き木 \(T\) が与えられたときに、各頂点に \(1, 2, 3\) のどれかを割り当てます。割り当てのコストを親よりも小さな値が割り当てられる頂点の数としたときに、コストが最小となる \(T\) への割り当てを求めるアルゴリズムを説明、解析してください。
-
燃え盛る犬の糞の大失敗を見たあなたは大急ぎで他の職を探し、Giggle を離れてそのライバル会社 Twitbook に移りました。不幸なことに、Twitbook の新しい社長は Giggle のホリデーパーティーと同じことをやってみようとちょうど決断したところで、あなたの過去の経験を見た社長はあなたを公式パーティーの幹事に抜擢しました。社長の命によると、社長を含むちょうど \(k\) 人の従業員を招待し、全員の参加を強制しなければならないとのことです。面白いことになってきました。
Giggle と同じように、 Twitbook の従業員の間は社長を根とした木で表される厳格な上下関係があります。また人事部にある全能のオラクルは全ての従業員の "気まずさ" を知っています。この値は従業員が直属の上司と上手く行っているかどうかを表します。例えば気まずさが負ならば、その従業員と直属の上司は上手く行っているということです。あなたの目標は従業員の中から \(k\) 人を選んで、気まずさの和が最小になるようにすることです。例えば招待した従業員の中にある従業員とその直属の上司の組が一つも無いなら、気まずさの和は \(0\) です。アルゴリズムの入力は木 \(T\), 整数 \(k\), 各頂点の気まずさです。
-
従業員の上下関係が二分木である、つまり全ての従業員に部下が最大でも二人しかいない場合に、\(k\) 人の従業員の部分集合で気まずさが最小となるものを計算するアルゴリズムを説明、解析してください。
-
❤ 従業員の上下関係に制約が無い場合に、\(k\) 人の従業員の部分集合で気まずさが最小となるものを計算するアルゴリズムを説明、解析してください。
-
-
根付き木の全ての頂点にメッセージを送りたいとします。最初にメッセージを知っているのは根の頂点だけで、各ラウンドでメッセージを知っている頂点は最大で一つの子にメッセージを送ることができます。例を次に示します:
 図 3.105 ラウンドでメッセージが木の全ての頂点に行き渡る様子
図 3.105 ラウンドでメッセージが木の全ての頂点に行き渡る様子-
メッセージを二分木に含まれる全ての頂点に届けるために必要な最小のラウンド数を計算するアルゴリズムを作ってください。
-
♦ メッセージを任意の根付き木に含まれる全ての頂点に届けるために必要な最小のラウンド数を計算するアルゴリズムを作ってください。 [ヒント: このアルゴリズムは貪欲アルゴリズムではありませんが、正しさの証明には次の章で説明するテクニックが役に立ちます。]
-
-
ある日、ジムの壁を登るのに飽きた Alex は、クライマーの友達を大勢誘って屋外の壁を登りに行きました。彼らが訪れたクライミングエリアはとても横にとても長い岩で、あまり高くはありませんでした。岩には手足を掛ける場所 (ホールド) がたくさんありましたが、それを見た Alex は友達と話し合って "許されている" 動きを設定しました。ホールドの間を移動するときには、このルールに従わなければなりません。
ホールドと許されている動きは \(n\) 頂点の根付き木 \(T\) で表され、頂点がホールドに、辺が許されているホールド間の動きを表します。岩を上る道は上に行くほど小さくなり、最終的にホールド一つになります。このホールドが \(T\) の根に対応します25。
Alex とその友達 (みな優秀なクライマーです) は、なるべく多い人数で岩を同時に上るというゲームをすることになりました。ただしクライマーはちょうど \(k\) 回だけ岩を上に向かって登らないといけません。つまり、クライマーは \(T\) の中で根に向かって長さ \(k\) の道を描きます。加えて、一つのホールドを使えるのは一人のクライマーだけです。つまりクライマーの軌跡が交差してはいけません。
このゲームをプレイできる最大人数を計算する効率の良いアルゴリズムを説明、解析してください。きちんと言うと、根付き木 \(T\) と整数 \(k\) が与えられたときに、\(T\) の根に向かう長さ \(k\) の互いに重ならない \(T\) の路からなる集合の最大の大きさを計算してください。 \(T\) が二分木だと仮定しないでください。次の例では \(k=3\) であり、アルゴリズムの出力は整数 \(8\) です。
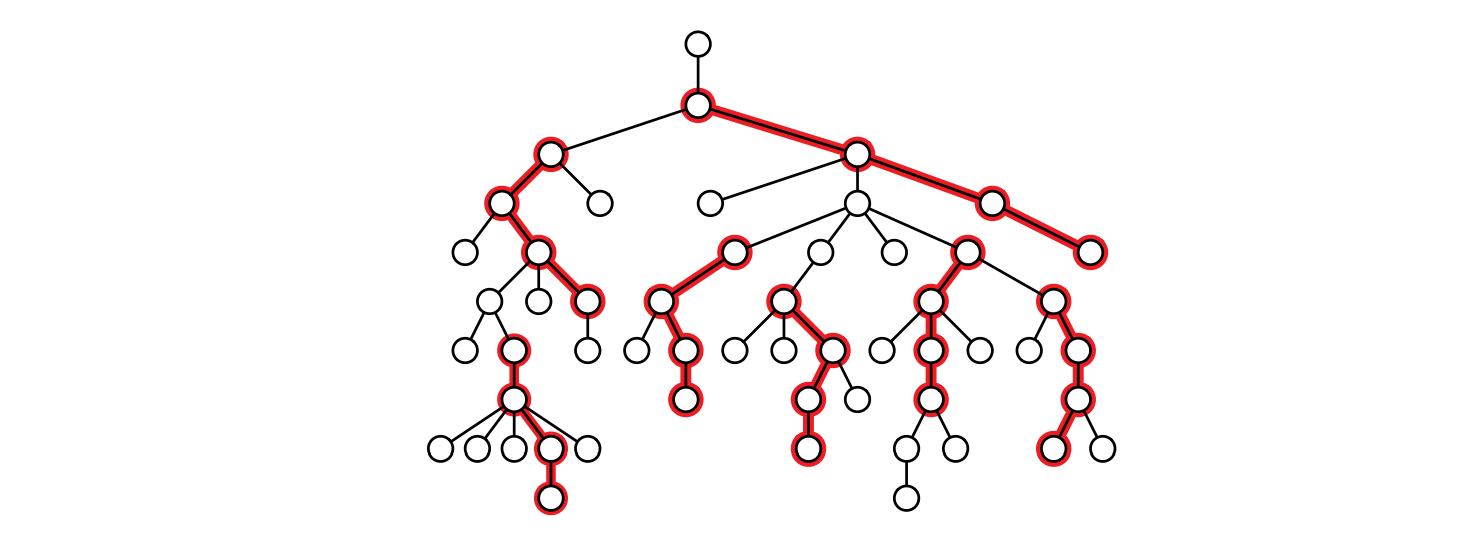 図 3.11長さが \(k=3\) である重ならない 7 つの道 (この集合は条件を満たす最大の集合ではない)
図 3.11長さが \(k=3\) である重ならない 7 つの道 (この集合は条件を満たす最大の集合ではない) -
\(T\) を \(n\) 頂点の根付き二分木、\(k \leq n\) を正の整数とします。 \(T\) の頂点のうち \(k\) 個に印をつけて、全ての頂点のなるべく近い祖先に印をつけた頂点があるようにしたいとします。きちんと言うと、\(T\) の頂点の部分集合 \(K\) に対するクラスタリングコストを次のように定義し、これを最小化します: \[ \mathit{cost}(K) = \max\limits_{v} \mathit{cost}(v, K) \] ここで \(\max\) は木に含まれる全ての頂点に関する最大値を表し、\(\mathit{cost}(v, K)\) は \(v\) から \(K\) に含まれる一番近い \(v\) の先祖までの距離です: \[ \mathit{cost}(v, K) = \begin{cases} 0 & \text{if } v \in K \\ \infty & \text{if } v \text{ が } T \text{ の根でかつ } v \notin K \\ 1 + \mathit{cost}(\mathit{parent}(v)) & \text{それ以外} \end{cases} \] この定義から、\(K\) が \(T\) の根を含まないならば \(\mathit{cost}(K) = \infty\) であることが分かります。
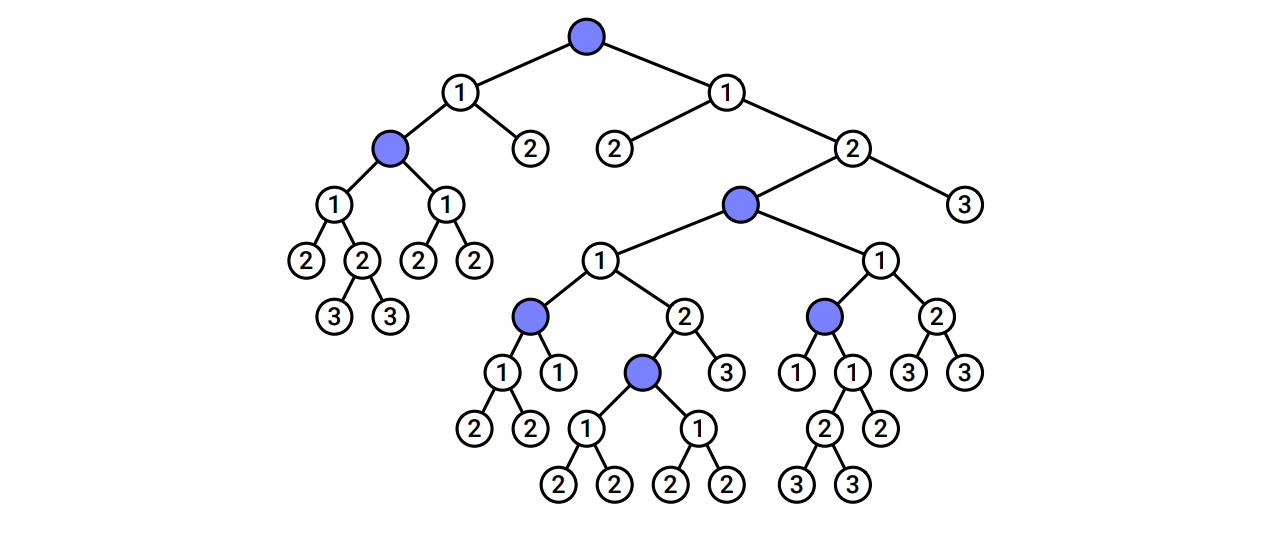 図 3.12二分木の頂点の部分集合 (大きさは \(5\) で、クラスタリングコストは \(3\))
図 3.12二分木の頂点の部分集合 (大きさは \(5\) で、クラスタリングコストは \(3\))-
❤ 木 \(T\) と整数 \(k\) が与えられたときに、\(k\) 頂点からなる \(T\) の頂点の部分集合の中でクラスタリングコストが最小のものを計算する動的計画法のアルゴリズムを説明してください。満点のためには、アルゴリズムの実行時間が \(O(n^{2}k^{2})\) であることが求められます。
-
木 \(T\) と整数 \(r\) が与えられたときに、クラスタリングコストが \(r\) 以下である \(T\) の頂点の部分集合で最小のものを計算する動的計画法のアルゴリズムを説明してください。満点のためには、アルゴリズムの実行時間が \(O(nr)\) であることが求められます。
-
(b) に対する答えを使うと (a) の問題に対する \(O(n^{2} \log n)\) 時間の答えを得られることを示してください。
-
-
この問題では与えられた二つの木に対する共通根付き部分木を求める問題を考えます。根付き木とは根と呼ばれる頂点を持つ連結非巡回グラフであることを思い出してください。根付き部分木とは、ある頂点とその全ての子孫からなる根付き木のことです。 "共通" の意味はどのような根付き木の組を同型 (isomorphic) とみなすかによって異なります。
-
二分木では各頂点が左の部分木と右の部分木を持っており、空の部分木も許されています。二つの二分木が同型とは、どちらも空であるか、そうでなければ左の部分木同士と右の部分木同士がどちらも同型であることを言います。二つの二分木が与えられたときに最大共通部分二分木を計算するアルゴリズムを説明してください。
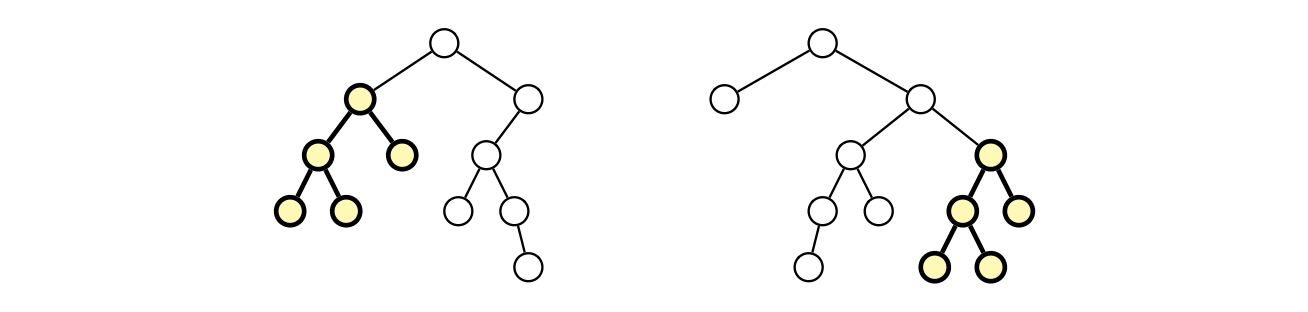 図 3.13二つの二分木 (最大共通部分二分木が強調してある)
図 3.13二つの二分木 (最大共通部分二分木が強調してある) -
順序付き根付き木 (ordered rooted tree) では各頂点が子の列を持っており、それぞれの子は順序付き根付き部分木の根です。二つの順序付き根付き木が同型とは、どちらも空であるか、そうでなければ全ての添え字 \(i\) について \(i\) 番目の部分木同士が同型であることを言います。二つの順序付き根付き木が与えられたときに最大共通順序付き根付き部分木を計算するアルゴリズムを説明してください。
-
♦ ❤ 順序無し根付き木 (unordered rooted tree) では各頂点が子の集合を持っており、それぞれの子は順序無し根付き木の根です。二つの順序無し根付き木が同型とは、どちらも空であるか、そうでなければ全ての添え字 \(i\) について \(i\) 番目の部分木同士が同型であるように二つの木の根の子を順序付けられることを言います。二つの順序無し根付き木が与えられたときに最大共通順序無し根付き部分木を計算するアルゴリズムを説明してください。
-
-
この問題では根無し木 ――連結非巡回無向グラフ―― の最適部分木を効率良く計算するアルゴリズムを考えます。根無し木の部分木とは任意の連結部分グラフのことです。
-
根無し木 \(T\) と辺の重みを与えられたとします。重みは正でもゼロでも負でもあり得るとしたとき、\(T\) 内の道であって最大の重みを持つものを求めるアルゴリズムを説明してください。
-
根無し木 \(T\) と頂点の重みを与えられたとします。重みは正でもゼロでも負でもあり得るとしたとき、\(T\) の部分木であって最大の重みを持つものを求めるアルゴリズムを説明してください。 [この問題は 2016 年の Google の面接試験で出題されました。]
-
\(T_{1}, T_{2}\) を任意の順序付き根無し木とします。つまり、各頂点に隣接する頂点の集合は well-defined な環状の順序を持っているということです。 \(T_{1}\) と \(T_{2}\) の最大共通順序付き部分木を求めるアルゴリズムを説明してください。
-
♦ ❤ \(T_{1}, T_{2}\) を任意の順序無し根無し木とします。 \(T_{1}\) と \(T_{2}\) の最大共通順序無し根無し部分木を求めるアルゴリズムを説明してください。
-
-
根付き木の根付きマイナー (rooted minor) とは部分列の自然な拡張です。根付き木 \(T\) の根付きマイナーとは一つ以上の辺を縮約 (contraction) してできる任意の木のことを言います。頂点 \(v\) とその親 \(u\) を結ぶ辺 \(u \to v\) を縮約すると、\(v\) の子が \(u\) の子となり、\(v\) は削除されます。また \(T\) の根は \(T\) の全ての根付きマイナーの根です。
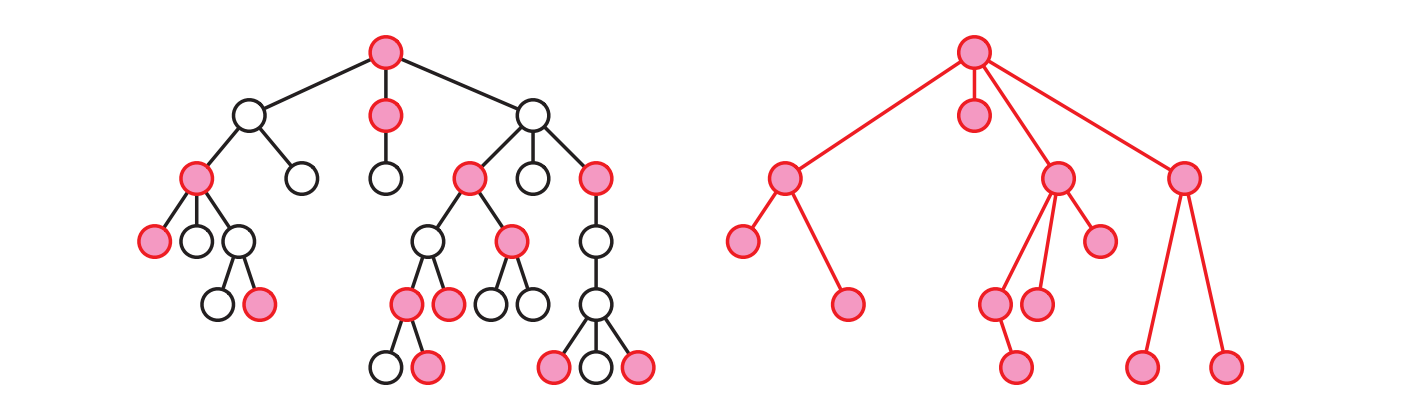 図 3.14根付き木とその根付きマイナーの一つ
図 3.14根付き木とその根付きマイナーの一つ-
\(T\) を頂点にラベルの付いた根付き木とします。 \(T\) の全ての頂点 \(x\) について、\(x\) の子が全て同じラベルを持っているとき、\(T\) は退屈である (boring) と言います (違う頂点の子は違うラベルを持っていて構いません)。与えられたラベル付き根付き木 \(T\) の退屈な根付きマイナーのうち最大のものを計算するアルゴリズムを説明してください。
-
\(T\) を頂点に数字のラベルが付いている根付き木とします。 \(T\) のヒープ順序付き (heap-ordered) 根付きマイナーのうち最大のものを計算するアルゴリズムを説明してください。つまり \(T\) の根付きマイナーを \(M\) とすると、アルゴリズムが返すのは、各頂点のラベルが子のラベルよりも小さいという条件を満たす \(M\) の中で最大のものです。
-
\(T\) を頂点に数字のラベルが付いている二分木とします。 \(T\) の二分探索順序付き (binary-search-ordered) 根付きマイナーのうち最大のものを計算するアルゴリズムを説明してください。つまり \(T\) の根付きマイナーを \(M\) とすると、アルゴリズムが返すのは、各頂点が最大で二つの子を持ち、\(M\) の通り掛け順の走査が (\(T\) の通り掛け順の走査の部分) 増加列となるような \(M\) のうち最大のものです。
-
根付き木が順序付いている (ordered) とは、各頂点の子が well-defined な左から右への順番を持っていることを言います。頂点が数字でラベル付けされた任意の順序付き木 \(T\) に対して、その最大二分探索順序付き根付きマイナーを求めるアルゴリズムを説明してください。アルゴリズムが答える根付きマイナー \(M\) の頂点における左から右への順序は \(T\) のものと一致している必要があります。
-
❤ 二つのラベル付けされた順序付き根付き木に対して、最大共通順序付き根付きマイナーを求めるアルゴリズムを説明してください。
-
♦ ❤ 二つのラベル付けされた順序無し根付き木に対して、最大共通順序無し根付きマイナーを求めるアルゴリズムを説明してください。 [ヒント: 動的計画法と最大フローを組み合わせてください。]
-
-
モールス信号では "ツー" が "トン" の三倍の長さを持ち、"ツー" と "トン" 両方の後に空拍が続きます。そのため "トン" が laghu akṣara に、"ツー" が guru akṣara に対応すると言えます。実際、モールス信号には四つの mātrā からなる文字がちょうど五つ (M, D, R, U, H) あります。[return]
-
Chandaḥśāstra には与えられた音節の数を持つ歩格を全て列挙する機械的な方法が二つ載っています。大まかに言うと数を二進法で表すことに対応し、一つは (ギリシャ人のように) 左から右に、もう一つは (エジプト人のように) 右から左に数を書いていきます。同じ部分にはこの他にも二乗を繰り返すことで \(2^{n}\) (\(n\) 音節に含まれる歩格の数) を計算する再帰的なアルゴリズム、そして二項係数 (\(k\) 個の軽い音節を含む、全体で \(n\) 音節の歩格の数) を計算する再帰的なアルゴリズムが含まれています (議論はありますが、おそらくは含まれています)。[return]
-
「実際の発見者の名前がつけられる科学的発見は存在しない」というのがスティグラー (Stigler) の法則です。この法則に名前が付けられた 1980 年の論文で、統計学者 Stephen Stigler (スティーブン・スティグラー) はこの法則を最初に発見したのは社会学者 Robert K. Merton (ロバート・K・マートン) であると冗談めかして書いています。しかし似たような発言はそれよりも前にされています: 1970 年代には Vladimir Arnol'd (ウラジーミル・アーノルド) によって (「発見が正しい人物に結びつけられることはほとんどない」)、1968 年には Carl Boyer (カール・ボイヤー) によって (「歴史の女神クレイオーは人名と定理を結び付けるときには気まぐれなことが多い」)、1917 年には Alfred North Whitehead (アルフレッド・ノース・ホワイトヘッド) によって (「重要なものはみな発見していない誰かによって言及されている」)、そして 1966 年にはなんと Stephen の父 George Stingler (ジョージ・スティグラー) によって (「定理に正しい人物の名前がつくことがもし万一あったら、特筆に値する」)。この本にはスティグラーの法則の例がたくさん出てきます。[return]
-
バックトラッキングで生じる再帰方程式を解く方法については http://algorithms.wtf/ を見てください。[return]
-
Michie は全てのプログラミング言語がサポートすべき抽象としてメモ関数 (memo function) を提案しました。メモ関数とは (通常の意味での) 関数 (rule) と辞書 (rote) という二つの要素からなり、ある入力に対する出力を初めて計算する場合には、出力を辞書にメモ (memorise、r が付く) してから値を返します。Michie はこのアイデアを、Samuel がチェッカーのゲーム木の再帰的な探索を高速化するために使った「暗記による学習 (rote learning)」 というテクニックから得ており、自身が行った一般的な提案を指して「プログラマーは好きな関数を "Samuelize" できるようになる」と説明しています (私が調べた限りでは、Michie 自身は "memoisation" という単語を一度も使っていません)。メモ化というテクニックは Samuel よりさらに前、1950 年に Claude Shannon (クロード・シャノン) が設計、構築した迷路を解く機械「テセウス (Theseus)」で使われています。[return]
-
動的計画法という一般的なテクニックは 1930 年代から 1940 年代にかけて独立に何度か発見されています。例えば Pierre Massé (ピエール・マス) はヴィシー政権のフランスにおいて、水力発電所の操業の最適化に動的計画法を使いました。John von Neumann (ジョン・フォン・ノイマン) と Oskar Morgenstern (オスカー・モルゲンシュテルン) は任意の二人対戦の完全情報ゲーム (例えばチェッカー) の勝者を判定するのに動的計画法を使いました。Alan Turing (アラン・チューリング) とその仲間たちはブレッチレー・パークで暗号を解読するときに同様の方法を使いました。Massé, von Neumann, Morgenstern が研究を最初に発表したのは 1944 年のことで、Bellman が "動的計画法" という言葉を思いつく 6 年前です。また Turing の "Banburismus" は 1980 年代中頃まで機密扱いでした。[return]
-
Charles Erwin Wilson (チャールズ・アーウィン・ウィルソン) は 1953 年、長い間務めたゼネラルモーターズの社長としての職を離れて国防長官となりました。 "エンジンの Charlie" と知られた彼は国防総省を事業法人のようにすることを明確な目標とした改革を就任初年から開始し、予算を大幅に縮小しました。Bellman は Wilson について、1984 年の自伝でこう書いています:
ワシントンには Wilson というとても興味深い紳士がいた。国防長官だった彼は、"研究" という単語に病理学的な恐怖と憎悪を抱いていた。私は "病理学的な" という言葉を軽々しく使っているつもりはない。彼の前で "研究" という単語を使おうものなら、彼の態度は一変して、顔は真っ赤になって、言葉遣いは乱暴になったものだ。彼が "数学" という単語についてどう感じていたか、簡単に想像が付くだろう。私がランド研究所で数学を研究していることを、どうにかして Wilson と空軍に隠さなければならないと私は感じていた。研究のタイトルは、そこで使う用語は、どうすればよいだろうか?
ただし Bellman が最初に "動的計画法" という言葉を使ったのは 1952 年の Wilson が就任する数か月前なので、この話は少し装飾されています。[return]
-
...あるいは Charles Atlas による有名なエクササイズ番組に対して 1928 年に Charles Roman がつけた象徴的な名前 "Dynamic Tension" にかけただけかもしれません。[return]
-
Chandaḥśāstra で Piṅgala が 2 のべきに対して使ったのと同じやり方です。[return]
-
They hardly ever ever work! Then give three cheers, and one cheer more, for the rigorous Captain of the Pinafore! Then give three cheers, and one cheer more, for the Captain of the Pinafore![return]
-
自分の講義でこのポリシーを導入したところ、生徒が正しくない貪欲なアルゴリズムを提出する回数が激減し、成績が劇的に向上しました。[return]
-
\(i < j\) が必ず成り立つので、本当はこの配列の半分しか必要になりません。定数時間の高速化についてはこの本で扱いませんが、仮に高速化を行うにしても、このタイミングで配列のサイズを削ることを考えるのは時期尚早です。「まず動くようにせよ。それから速くせよ」[return]
-
言ったでしょう、定数部分は気にするなって![return]
-
このアルゴリズムが Saul Needleman (ソール・ニードルマン) と Christian Wunsch (クリスチャン・ウンシュ) によって発見されたとされることがありますが、これは間違っています。また "Needleman-Wunsch のアルゴリズム" が、二つの文字列の最長共通部分列 (挿入と削除だけが許された時の編集距離) を計算する通常の動的計画法のアルゴリズムであると説明されることがありますが、これも間違っています。Needleman-Wunsch のアルゴリズムとは、重み付けされた、空白を許す最長共通部分列を \(O(m^{2}n^{2})\) 時間で計算するものであり、再帰方程式も異なります。 Sankoff は自身の \(O(mn)\) 時間のアルゴリズムが Needleman-Wunsch のアルゴリズムを改善したものであると明示的に説明していました。[return]
-
ええ、速すぎる最適化に関する自分のルールを破っています。[return]
-
部分和問題は NP 困難ですが、この実行時間の上限をもって P = NP と結論することはできません。 \(T\) を入力サイズの多項式関数で抑えることができないためです。[return]
-
1967 年、Donald Michie はメモ関数を提案した研究の覚書 (!) でこう書いています: 「必要ない関数の値を記録するのは空間の無駄使いであり、同じ値をもう一度計算するのは時間の無駄使いである」 しかし実際には、必要のない関数の値を記録することは時間の無駄でもあります![return]
-
私のアルゴリズムの講義では、動的計画法の解答にそれが解いている再帰的な小問題に対する英語で書かれた仕様が含まれていない場合、それ以外の答案が完璧であったとしても自動的に点数がゼロになります。このポリシーを導入したところ、生徒が間違った (あるいは支離滅裂な) 動的計画法のアルゴリズムを提出する回数が激減し、成績が劇的に向上しました。[return]
-
Nadiria の歴史と文化および夢ドル紙幣の画像は http://moneyart.biz/dd/ から参照できます。[return]
-
北コースを使えばスピードがもっと出ますが、対決に使うには短すぎます。[return]
-
Vaikin's killometer にさらに上方向の移動を加えた場合、このゲーム (Vankin's Fathom?) は NP 困難となります。[return]
-
もっと洗練されたテクニックを使えば実行時間を \(O(n^{3 / 2} \log \log n)\) にできると私は信じていますが、まだ詳細を詰め切っていません。[return]
-
Sedgewick の提案したデータ構造は右の子が赤くてはいけないという制約を持っていましたが、まぁ、どうでもいいです。奇妙なことに、Andersson と Sedgewick は両人とも角度を測るときに時計周りに測るかそれとも反時計回りに測るか、冥王星が惑星がどうか、"lower rank" が意味するのが良いことなのかそれとも悪いことなのか、アヒルサイズの馬 100 匹と馬サイズのアヒル 1 匹だったらどちらと戦いたいかについては沈黙したままです。[return]
-
最悪探索時間 \(O(\log_{B} n)\) を保証するには、これらの他に二つの制約が必要となります: (1) 全ての葉が同じ深さを持つ (2) 根を除く全ての頂点が \(B / 2\) 個以上の鍵を持つ。しかしこの問題で考えているのは最悪探索時間ではなく合計探索時間なので、追加の制約は課しません。[return]
-
Q: どうしてあなたたち情報科学の教授は木の根が上にあると思っているのですか? A:外に出たことがないから![return]