クリークと頂点被覆 (最大独立集合からの帰着)

クリーク (clique) とはグラフに含まれる完全グラフ、つまり任意の頂点の組の間に辺がある部分グラフのことであり、\(\textsc{MaxClique}\) 問題とはグラフに含まれる最大のクリークの大きさを求める問題です。頂点被覆 (vertex cover) とはグラフの全ての辺に触れるような頂点の集合であり、\(\textsc{MinVertexCover}\) 問題とはグラフに含まれる最小の頂点被覆の大きさを求める問題です。

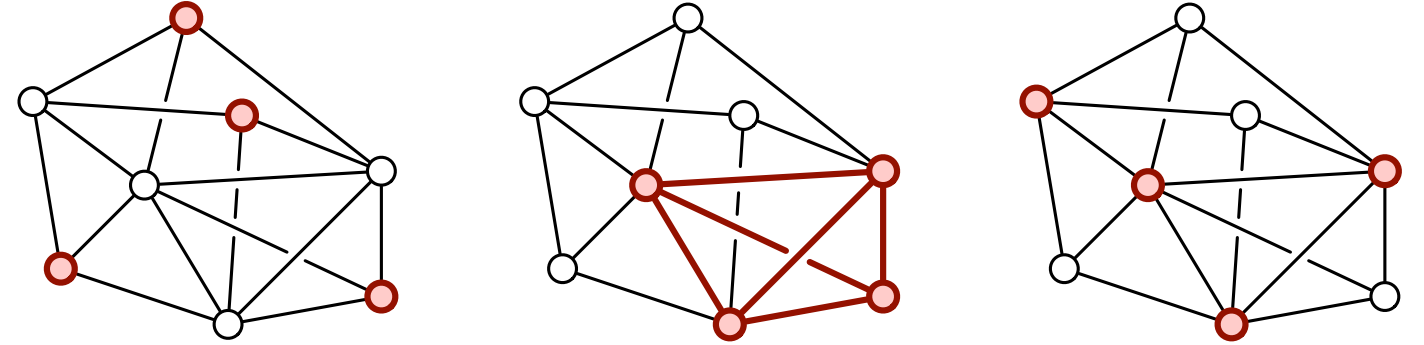
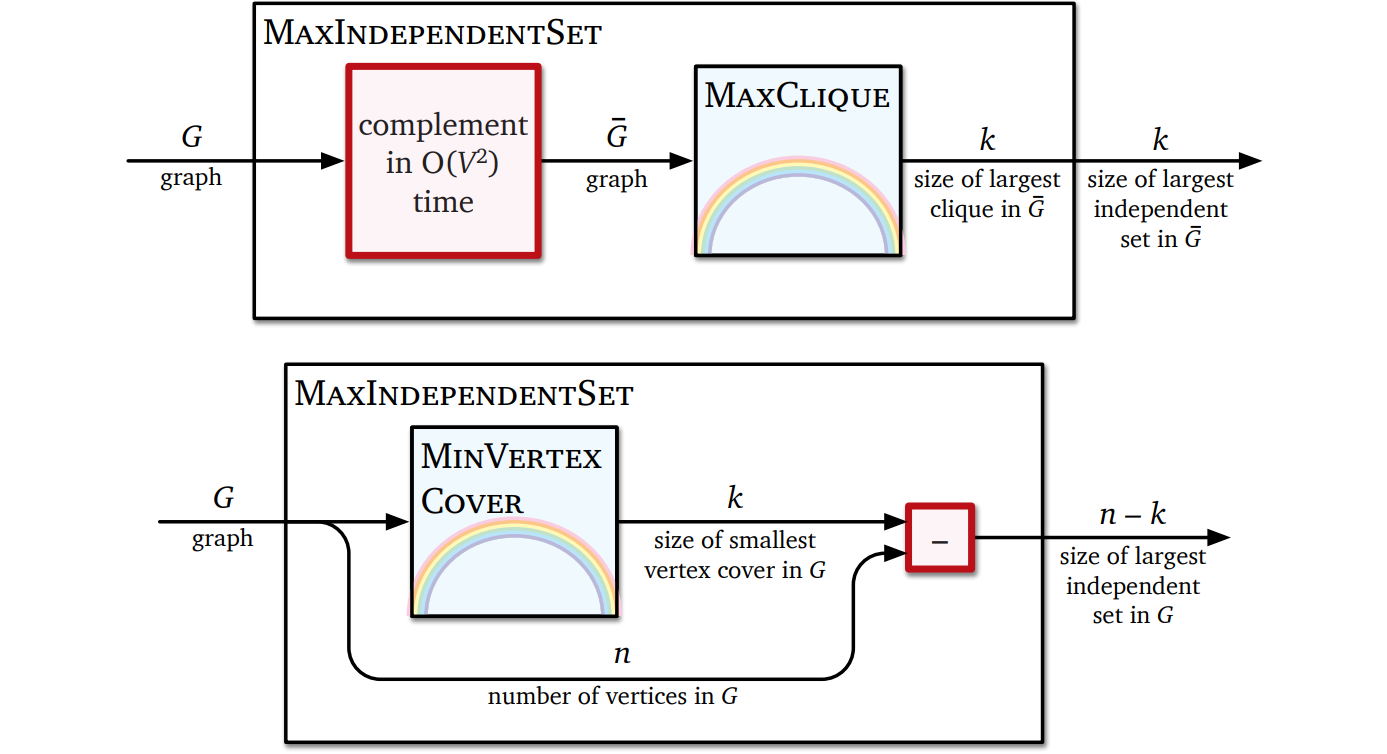
\(\textsc{MaxClique}\) が NP 困難であることは \(\textsc{MaxIndSet}\) からの簡単な帰着によって示せます。任意のグラフ \(G\) の辺の有無を反転させたものを辺補グラフ (edge-complement graph) \(\overline{G}\) と言います ―― \(\overline{G}\) の頂点は \(G\) と同じで、\(uv \in \overline{G}\) \(\iff\) \(uv \notin G\) です。\(G\) における最大独立集合は辺補グラフ \(\overline{G}\) における (同じサイズの) 最大クリークとなるので、帰着は簡単に作れます。

\(\textsc{MinVertexCover}\) が NP 困難であることの証明はさらに簡単です: グラフ \(G=(V,E)\) の独立集合を \(I\) とすると、その補集合 \(V \backslash I\) は同じグラフ \(G\) の頂点被覆となります。よってグラフの最大独立集合は同じグラフの最小頂点被覆の補集合です！ \(n\) 頂点のグラフの最小頂点被覆の大きさが \(k\) ならば、最大独立集合の大きさは \(n-k\) となります。