掛け算

アルゴリズムが正式な学術研究の対象となってまだ数十年しか経っていませんが、人類は文明が始まった頃からアルゴリズムを使ってきました。計算手順の詳細な説明は人類が言語を書き留めた最も古い例の一つです。それは Fibonacci や al-Khwārizmī よりもずっと前のことで、彼らが広めた位取り記数法よりもさらに前のことです。

格子掛け算

少なくとも多くのアメリカ人の学生にとって、大きな整数を掛け算する方法として一番なじみ深いのは格子掛け算 (lattice multiplication) です。このアルゴリズムは Fibonacci の著作 Liber Abaci によって広まりました。

Fibonacci はこのアルゴリズムを al-Khwārizmī などのアラビアの文献から得ており、al-Khwārizmī などのアラビアの数学者が学んだのは七世紀に Brahmagupta (ブラフマグプタ) によって書かれた Brāhmasphuṭasiddhānta (ブラフマースプタシッダーンタ) をはじめとするインドの文献です。さらにインド人の数学者が中国の文献から学んでいたという可能性もあります。

格子アルゴリズムを説明した現存する最古の資料は、三世紀から五世紀の間に中国で書かれた『孫子算経』、および起源 500 年ごろに Eutocius of Ascalon (アシュロンのユートキアス) によって書かれた Archimedes (アルキメデス) の『円の計測』に対する注釈です。しかしそれよりもずっと以前から使われていたことを示す資料があります。Eutocius は格子アルゴリズムの考案者として紀元前 300 年ごろの人物 Apollonius of Perga (ペルガのアポロニウス) とその著作 \(\Omega \kappa \upsilon \tau \acute{o} \kappa \iota o \nu\)¹ (オキトキオン) に言及しています (この文献は現存しません)。またシュメール人は紀元前 2600 年ごろには既に乗算表を粘土板に記録しており、格子アルゴリズムが使われていた可能性があります²。

格子アルゴリズムは入力の数が桁ごとに数字を並べた文字列で表されることを仮定します。ここでは 10 進法を使いますが、格子アルゴリズムは簡単に任意の底に一般化できます。表記を簡単にするために、入力が \(X[0..m-1]\) と \(Y[0..n-1]\) という配列の組であり³、それぞれ \[ x = \sum_{i=0}^{m-1} X[i] \cdot 10^{i}, \quad y = \sum_{j=0}^{n-1} Y[j] \cdot 10^{j} \] という数を表すとします。そして出力も同じように \(Z[0..m+n-1]\) であり、 \[ z = x \cdot y = \sum_{k=0}^{m+n-1} Z[k] \cdot 10^{k} \] という積を表すとします。

格子アルゴリズムは足し算と一桁の掛け算を基本演算として使います。足し算は一段の for ループで計算し、一桁の掛け算にはルックアップテーブルを使うことが多いです。ルックアップテーブルを使うとはつまり、掛け算の値を事前に粘土板に刻んだり、木簡や竹簡あるいは紙に書いたり、読み込み専用のメモリに書き込んだり、計算者 (computator) が記憶したりするということです。

格子掛け算のアルゴリズムは次の式で要約できます: \[ x \cdot y = \sum_{i=0}^{m-1} \sum_{j=0}^{n-1}(X[i] \cdot Y[j] \cdot 10^{i+j}) \] 異なる格子アルゴリズムは部分積 \(X[i] \cdot Y[j] \cdot 10^{i+j}\) を異なる順番で計算したり、和の計算に異なる方法を使ったりします。例えば Liber Abaci で Fibbonacci が説明したのは \(mn\) 個の部分積を小さい順に計算する方法であり、次の疑似コードで表されます:

Fibonacci のアルゴリズムを人間が実行するときには、部分積を (「タブロー」とか「格子」とか呼ばれる) 二次元の表に記録し、対角線に沿って繰り上りを考えながら足して最終的な答えを計算するという方法がよく使われます。この様子を図 0.1の右側に示します。この図の左側に示すのは、一方の数 (掛けられる数) をもう一方の数 (掛ける数) の各桁で掛け、その結果を縦に並べて書いてからまとめて足すという方法です。これは現代のアメリカの小学校で教えられている方法であり、Eutocius によっても説明されています。ただし図 0.2に示すように、Eutocius の時代には数を左から右に書きました。

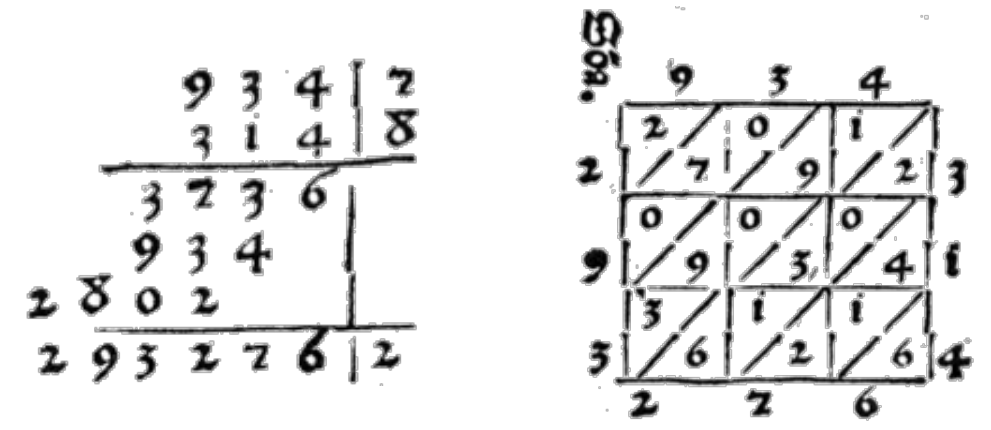
これら二つのアルゴリズムは両方とも (いくつかの別種と共に) 1458 年の作者不詳の教本 L'Arte dell'Abbaco で説明され、並んで図も載っています。この本は Treviso Arithmetic としても知られており、西洋で最初の印刷された数学書です。

こういった格子アルゴリズムの変種 ――Sunzi, al-Khwārizmī, Fibonacci, L'Arte dell'Abbaco および他のたくさんの資料で見られる似たようなアルゴリズム―― は全て、任意の \(m\) 桁の数と \(n\) 桁の数の積を \(O(mn)\) 時間で計算し、実行時間は一桁の掛け算の数によって支配されます。

Duplation と Mediation

格子アルゴリズムは直接的な記録が残っている最古の乗算アルゴリズムではありません。これよりもさらに古く、そして明らかにより単純なアルゴリズムが存在します。それは "ロシア農民の掛け算" または "エチオピア農民の掛け算"、あるいは単純に農民の掛け算 (peasant multiplication) と呼ばれるアルゴリズムであり、このアルゴリズムは位取り記数法を必要としません。

エジプト人書記官 Ahmes (アーメス) がこのアルゴリズムの一種をリンド数学パピルスと呼ばれる文書に書き写したのは紀元前 1650 年前後のことです。その中で彼は、このアルゴリズムが当時約 350 年前から知られていたと記しています⁶。東欧の小学校では二十世紀の終わりごろまでこのアルゴリズムが実際に教えられていました。また整数乗算がハードウェアで実装されていない初期のデジタルコンピューターで乗算の計算に使われていたのもこのアルゴリズムです。

農民の掛け算アルゴリズムは任意の数の掛け算という難しいタスクを 4 つの簡単な操作の列に置き換えます。つまり (1) パリティ (奇数か偶数か) の検査、(2) 足し算、(3) duplation (数を2倍する)、(4) mediation (数を2で割って、小数部分を切り捨てる) です。疑似コードを次に示します:

このアルゴリズムの正しさは、非負整数 \(x\) と \(y\) に関する次の再帰的な等式と帰納法から従います: \[ x \times y = \begin{cases} 0 & \text{if } x = 0 \\ \lfloor x / 2 \rfloor \times (y + y) & \text{if } x \text{ が偶数} \\ \lfloor x / 2 \rfloor \times (y + y) + y & \text{if } x \text{ が奇数} \\ \end{cases} \] この再帰方程式が農民の掛け算アルゴリズムそのものであるとも言えるでしょう。疑似コードのループに惑わされないでください: このアルゴリズムは本質的に再帰的です！

上述の通り、\(\textsc{PeasantMultiply}\) はパリティ検査と足し算と mediation 演算を \(O(\log x)\) 回行います。ここで \(x > y\) のときに \(x\) と \(y\) を取り換えることで、この回数を \(O(\log \min\lbrace x, y \rbrace)\) にできます。さらに底が大きすぎない位取り記数法 (二進法、十進法、バビロニアの六十進法、エジプトの十二進法、ローマ数字、中国の算木) を使って数を表していると仮定すれば、それぞれの基本演算は最大 \(O(\log (xy)) =\) \(O(\log \max\lbrace x, y \rbrace)\) 回の一桁の演算を必要とします。よってアルゴリズム全体の実行時間は \(O(\log \min \lbrace x, y \rbrace \cdot \log \max\lbrace x, y \rbrace) =\) \(O(\log x \cdot \log y)\) となります。

これを言い換えると、農民の掛け算アルゴリズムを使って \(m\) 桁の数と \(n\) 桁の数の積を計算するのにかかる時間は、定数を無視すれば \(O(mn)\) であり、格子アルゴリズムと同じであるということです。農民の掛け算アルゴリズムの実行には紙上での処理が (定数倍の範囲で！) より多く必要になりますが、必要となる基本演算 (パリティ検査、足し算、duplation、mediation) は人間にとって明らかにより簡単です。また二進法表記を使った場合には、二つのアルゴリズムは全く同じ操作となります。

コンパスと定規

古典ギリシャの幾何学者は数 (正確には大きさ) を対応する長さを持つ線分と同一視していました。彼らが線分を作成するときに使ったのは、測量技師や建築家などの職人によって既に数世紀に渡って使われていた単純な工作機械 ――コンパスと定規―― です。当時の学者は複雑な幾何学図形の作図をコンパスと定規だけを使った以下の基本処理に分解しました。この処理は一つ以上の固定された参照点から始まります。

• 既知の異なる二点の間に (唯一の) 直線を引く。
• 既知の点を中心とし、別の既知の点を通る (唯一の) 円を描く。
• 二つの直線の交点を (存在すれば) 得る。
• 円と直線の交点を (存在すれば) 得る。
• 二つの円の交点を (存在すれば) 得る。

ギリシャで幾何学を学ぶ学生が実際に作図を行うときには、ほとんどの場合アバカス (\(\ddot{\alpha} \beta \alpha \xi\)) というちりや砂に覆われたテーブルが使われました⁷。エジプトの測量技師もロープを使って直線と円を書くことでギリシャ人と同様の作図をギリシャ人より数世紀前に行っていました⁸。しかし Euclid を含むギリシャ人幾何学者が違っていたのが、コンパスと定規による作図を正確な数学的抽象概念とみなした点です ――点は理想的な点であり、直線は理想的な直線であり、円は理想的な円である、というように。

約 2500 年前に Euclid が『原論』で説明したアルゴリズムを次に示します。このアルゴリズムは二つの大きさを掛けるか割るかします: 入力は既知の点 \(A, B, C, D\) であり、出力として \(|AZ| = |AC||AD|/|AB|\) となる点 \(Z\) を作図します。 \(|AB|\) を単位長とすれば、このアルゴリズムで \(|AC|\) と \(|AD|\) の積を計算できます。

Euclid が \(\textsc{RightAngle}\) という新しい基本処理をサブルーチン (と現代のプログラマーが呼ぶであろうもの) として最初に定義している点に注目してください。このアルゴリズムの正しさは三角形 \(ACE\) と \(AZF\) が相似なことから従います。なおアルゴリズムのメイン処理の 2, 3 行目は円と直線の交点を求めているにもかかわらず二つの交点のどちらを選択するのかを示しておらず曖昧ですが、交点 \(E\) と \(F\) としてどちらを選んでもこのアルゴリズムは正しく動きます。

⟨⟨\(P\) を通り \(l\) に垂直な直線を作図する⟩⟩

procedure \(\texttt{RightAngle}\)(\(l, P\))

点 \(A \in l\) を選ぶ

\(A, B \leftarrow\)\(\texttt{Intersect}\)(\(\texttt{Circle}\)(\(P, A\)),\(\,\)\(l\))

\(C, D \leftarrow\)\(\texttt{Intersect}\)(\(\texttt{Circle}\)(\(A, B\)),\(\,\)\(\texttt{Circle}\)(\(B, A\)))

return \(\texttt{Line}\)(\(C, D\))

\(\ \)

⟨⟨\(|AZ| = |AC||AD|/|AB|\) を満たす点 \(Z\) を作図する⟩⟩

procedure \(\texttt{MultiplyOrDivide}\)(\(A, B, C, D\))

\(\alpha \leftarrow \)\(\texttt{RightAngle}\)(\(\texttt{Line}\)(\(A, C\)), \(A\))

\(E \leftarrow\)\(\texttt{Intersect}\)(\(\texttt{Circle}\)(\(A, B\)), \(\alpha\))

\(F \leftarrow\)\(\texttt{Intersect}\)(\(\texttt{Circle}\)(\(A, D\)), \(\alpha\))

\(\beta \leftarrow \)\(\texttt{RightAngle}\)(\(\texttt{Line}\)(\(E, C\)), \(F\))

\(\gamma \leftarrow \)\(\texttt{RightAngle}\)(\(\beta, F\))

return \(\texttt{Intersect}\)(\(\gamma, {}\)\(\texttt{Line}\)(\(A,C\)))

図 0.4

コンパスと定規を使った掛け算

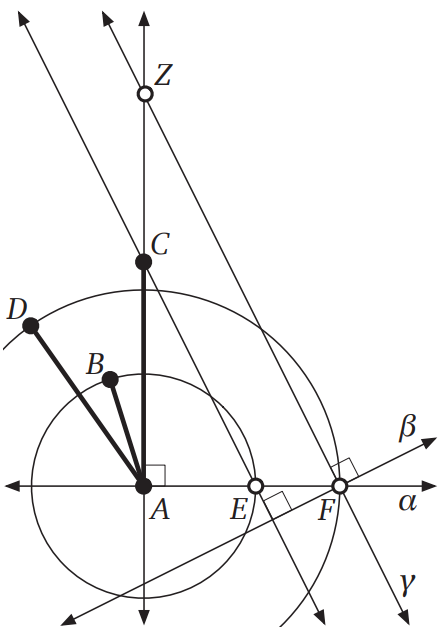
Euclid のアルゴリズムは、二つの大きさ (長さ) の掛け算をコンパスと定規を使った一連の基本処理に帰着させます。この処理をデジタルコンピューターで正確に行うのは困難ですが、Euclid のアルゴリズムはデジタルコンピューターで実行するように設計されたわけではありません。そうではなく、このアルゴリズムはプラトンの理想的なコンパスと定規を使って基本処理を完璧な正確さで実行する、理想的な幾何学のために設計されています。理想的な幾何学者は定義により基本処理を定数時間で実行するので、この計算モデルにおける \(\textsc{MultiplyOrDivide}\) の実行時間は \(O(1)\) です！

1. タイトルを直訳すると『安産のための薬』！ Pappus of Alexandria (アレキサンドリアのパップス) という人物が Eutocius よりも約 200 年前に同じ本 \(\Omega \kappa \upsilon \tau \acute{o} \kappa \iota o \nu\) の抜粋をいくつか複写したという記録が残っています。しかしその抜粋が格子アルゴリズムの説明を含んでいるかは分かっておらず、この抜粋も失われていています。^[return]

2. シュメール人が巨大な数の計算を 60 進の位取り記数法で正確に行っていたことについては十分な証拠があります。しかし彼らが実際に使った計算方法についての現存する記録を私は見たことがありません。また通常の乗算表と逆数表に加えて 1 から 59 までの整数の二乗を刻んだ表が見つかっており、このことをもってバビロニア人が \(xy = ((x + y)^2 - x^2 - y^2) / 2\) のような等式を使って乗算を計算していたとする数学史家もいます。しかしこのテクニックが使えるのは \(x < 60\) のときだけであり、バビロニア人が \(x > 60\) についてどのように \(x^2\) を計算していたのかは分かりません。^[return]

3. これによって歴史的な対立を焚き付けてしまうかもしれません: ギリシャ人とエジプト人、リリパット人とブレフスキュ人、Mac と PC、ゼロが自然数に含まれると考える人と間違っている人。^[return]

4. ソース: Biblioteca nazionale Braidense (Milano) (パブリックドメイン)。^[return]

5. ソース: https://archive.org/details/archimedisopera05eutogoog/page/n377 (パブリックドメイン)。^[return]

6. リンド数学パピルスに記されているアルゴリズムは mediation とパリティを使いませんが、比較は使います。このアルゴリズムは事前に二つの表を作成しておくことで、数を 2 で割らなくても済むようにしています。表の一つは \(x\) より小さい 2 のべきを並べたもので、もう一つの表はその 2 のべきに \(y\) を掛けたものです。貪欲な引き算によって \(x\) を分解したときに現れる 2 のべきが一つ目の表から選ばれ、それに対応する二つ目の表の要素を足し上げることで積が計算されます。^[return]

7. 1 から 9 までの数字は Fibonacci の Liber Abaci より少なくとも二世紀前から「ゴバール数字 (gobar numerals)」という名前でヨーロッパに知られていました。この名前はちりを意味するアラビア語 ghubār から取られており、意味をたどっていくと砂で覆われたテーブルを使って計算を行うインド人の習慣にたどり着きます。またギリシャ語の \(\ddot{\alpha} \beta \alpha \xi\) の語源はラテン語の abacus であり、これも元々は砂で覆われたテーブルを指します。^[return]

8. 幾何学を表す英単語 "geometry" が何を意味するか覚えていますか？ Democritus (デモクリトス) は後にエジプト人測量技師のことをいくらか嘲笑的に arpedonaptai (\(\acute{\alpha} \rho \pi \varepsilon \delta o \nu \acute{\alpha} \pi \tau \alpha \iota\)) と呼びました。これは "ロープを絞める人" を意味します。^[return]