最大独立集合 (3SAT からの帰着)

これから考えるいくつかの問題において、入力は単純重み無し無向グラフ、出力は何らかの構造的な特徴を持つ部分グラフのうち最大または最小のものです。

\(G\) を任意のグラフとします。\(G\) の独立集合 (independent set) とは、\(G\) の頂点の集合でどの頂点の組の間にも辺が無いものを言います。最大独立集合問題、略して \(\textsc{MaxIndSet}\) は与えられたグラフに含まれる最大の独立集合の大きさを求める問題です。これから \(\textsc{MaxIndSet}\) が NP 困難であることを \(\textsc{3SAT}\) からの帰着を使って示します:

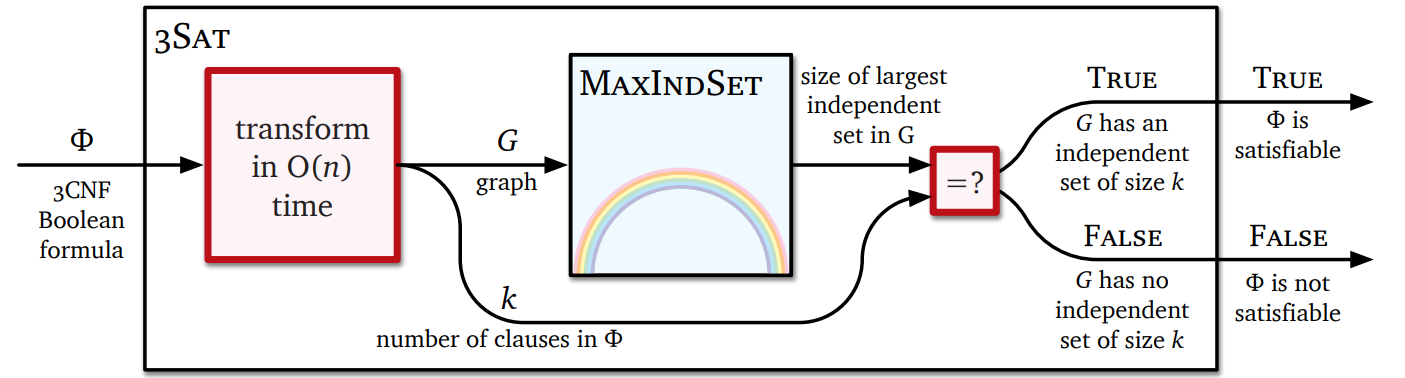
任意の 3CNF 式 \(\Phi\) が与えられたとき、次のようにしてグラフ \(G\) を構築します。\(\Phi\) に含まれる節の数を \(k\) とすると \(G\) には \(3k\) 個の頂点があり、それぞれが \(\Phi\) のリテラルに対応します。\(G\) の任意の二つの頂点の間に辺があるのは (1) 二つの頂点が同じ節にある、もしくは (2) 二つの頂点がある変数とその否定である、場合のみです。例えば \((a ∨ b ∨ c)\ ∧\) \((b ∨ \overline{c} ∨ \overline{d})\ ∧\) \( (\overline{a} ∨ c ∨ d)\ ∧\) \((a ∨ \overline{b} ∨ \overline{d})\) という式は次のグラフに変形されます:

図 12.6

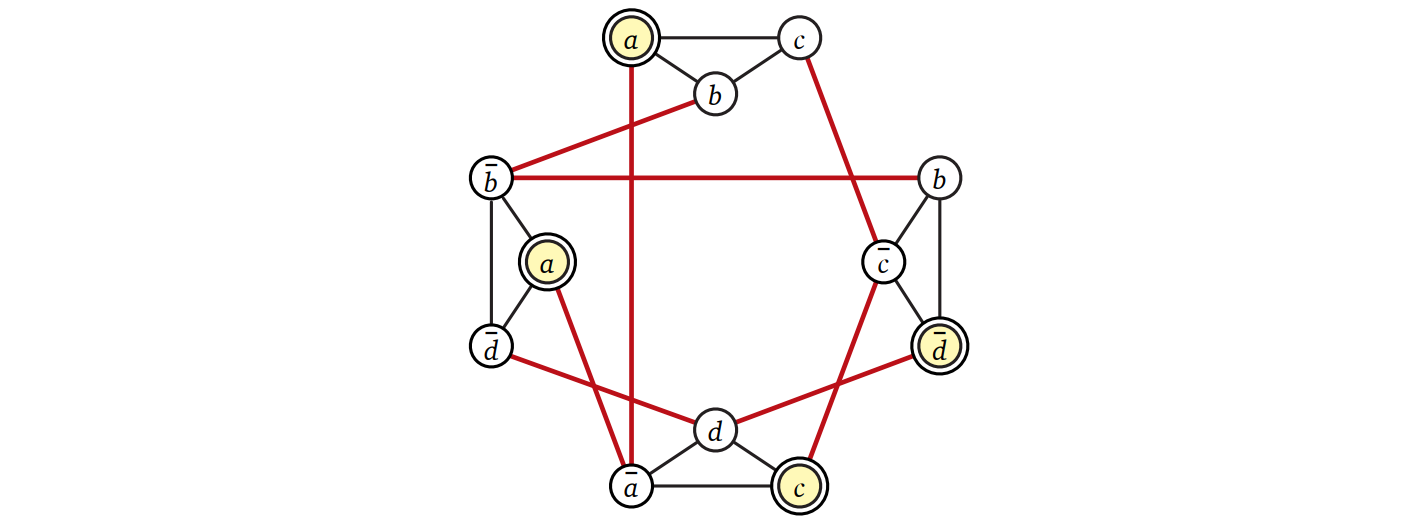
4 つの節を持つ充足可能な 3CNF 式から作られるグラフ (独立集合の大きさは 4)

\(\Phi\) の節に含まれる三つのリテラルに対応する \(G\) の頂点は全て辺で結ばれて三角形を作るので、\(G\) の独立集合はグラフの各三角形につき最大でも一つしか頂点を含みません。よって \(G\) の最大独立集合の大きさは最大でも \(k\) です。これから「\(G\) に大きさ \(k\) の独立集合が存在する」と「元の式 \(\Phi\) が充足可能である」が同値であることを示します。 "同値である" ことの証明の常として、証明は二つの部分からなります。

\((\Rightarrow)\) \(\Phi\) が充足可能だと仮定する。\(\Phi\) を充足させる適当な真偽値割り当てを取ると、\(\Phi\) の全ての節には少なくとも一つの \(\textsc{True}\) のリテラルが含まれる。よってそのようなリテラルを集めることで、大きさが \(k\) の \(G\) の頂点の部分集合であって頂点全てが異なる三角形に含まれるものが作ることができる。この集合を \(S\) とすると、\(S\) の各頂点は異なる三角形に含まれることから、\(S\) の任意の頂点の組の間には三角形の辺がない。また \(S\) に含まれる頂点は全て \(\textsc{True}\) のリテラルに対応するから、\(S\) の任意の頂点の組の間にはあるリテラルとその否定を結ぶ辺もない。したがって \(S\) は大きさ \(k\) の \(G\) の独立集合である。
\((\Leftarrow)\) \(G\) が大きさ \(k\) の独立集合 \(S\) を持つとする。\(G\) の三角形は辺で結ばれていることから、\(S\) の各頂点は異なる三角形に含まれていなければならない。あるリテラルとその否定の間には辺が存在することから、\(S\) に含まれるリテラル全てに \(\textsc{True}\) を割り当てるような真偽値割り当てを考えることができる。ただし \(x\) と \(\overline{x}\) がどちらも \(S\) に含まれないようなリテラルがあった場合には、適当な値を割り振ることにする。こうして出来上がる真偽値割り当てでは \(\Phi\) の全ての節に少なくとも一つの \(\textsc{True}\) リテラルが含まれるので、\(\Phi\) は充足可能だと分かる。

3CNF 式 \(\Phi\) のグラフ \(G\) への変換は、総当たりを使ったとしても多項式時間で行えます。よって \(\textsc{3SAT}\) の入力 \(\Phi\) をグラフ \(G\) に変換した上で \(G\) に含まれる最大独立集合の大きさと \(\Phi\) に含まれる節の数を比べるという方法を使えば、\(\textsc{MaxIndSet}\) を多項式時間で解けるときに \(\textsc{3SAT}\) を多項式時間で解くことができます。もしそうならば P=NP なので、何かがおかしいです！よって \(\textsc{MaxIndSet}\) は NP 困難だと結論できます。