Jarník の (Prim の) アルゴリズム
次に古い最小全域木アルゴリズムはチェコ人数学者 Vojtěch Jarník (ヴォイチェフ・ヤルニク) によって 1925 年に、Borůvka に送った手紙の中で初めて示されました。Jarník は翌年にこの発見を公表しています。同じアルゴリズムは Joseph Kruskal (ジョゼフ・クラスカル) によって 1956 年に、(おそらくは) Robert Prim (ロバート・プリム) によって 1957 年に、Harry Lobermand (ハリー・ロバーマンド) と Arnold Weinberger (アーノルド・ワインバーガー) によって 1957 年に、そして Edsger Dijkstra (エドガー・ダイクストラ) によって 1958 年にそれぞれ独立に再発見されました。Prim, Lobermand, Weinberger, Dijkstra は後に Kruskal の論文のことを知り、引用もしていますが、Kruskal は同じ論文で他に二つの最小全域木アルゴリズムを提案していたので、このアルゴリズムは "Prim のアルゴリズム" あるいは "Prim/Dijkstra のアルゴリズム" と呼ばれることが多いです (1958 年当時 Dijkstra には自分の名前が (事実に反する形で) 付けられた別のアルゴリズムが既にあったのですが)。
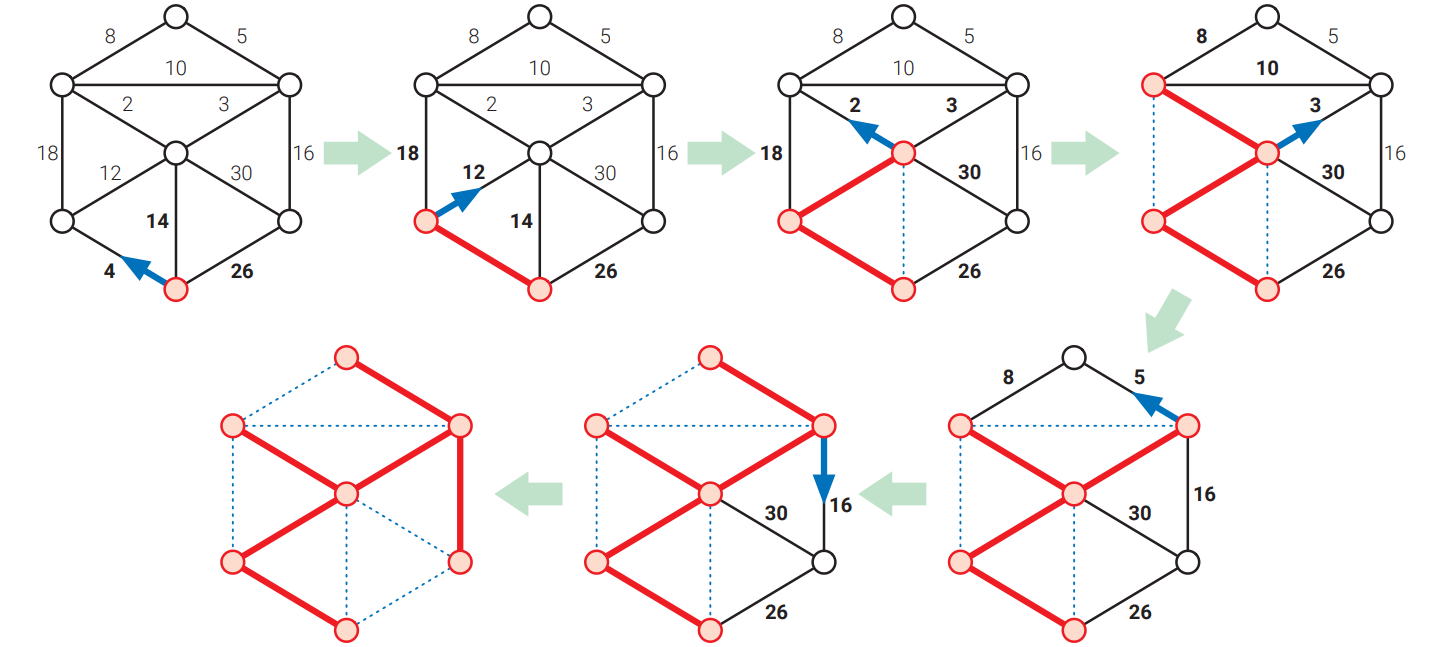
Jarník のアルゴリズムでは中間全域森 \(F\) の自明でない成分は一つしか存在せず、他の成分は全て孤立した頂点です。この自明でない成分 \(T\) は最初適当な頂点であり、次に示すステップを \(T\) が全域木になるまで反復します:
Jarník: \(T\) の安全な辺を \(T\) に足す。
Jarník のアルゴリズムの実装では \(T\) に隣接する辺を保持する優先度付きキューを管理します。アルゴリズムの各反復で最小の重みを持つ辺を優先度付きキューからポップし、まずその辺の両端点が \(T\) に入っているかを調べ、もしそうでなければその辺を \(T\) に加え、その頂点に隣接する辺を優先度付きキューにプッシュします。言い換えると、Jarník のアルゴリズムは 五章で説明した "最良優先探索" の一種です! 優先度付きキューを通常の二分ヒープを使って実装すれば、Jarník のアルゴリズムの実行時間は \(O(E \log E) = \pmb{O(E \log V)}\) となります。
❤ Jarník のアルゴリズムの改善
フィボナッチヒープ (fibonacci heap) というより複雑な優先度付きキューのデータ構造を使うと、Jarník のアルゴリズムを改善できます。フィボナッチヒープは Michael Fredman (マイケル・フレッドマン) と Robert Tarjan (ロバート・タージャン) によって 1984 年に提案されました。二分ヒープと同様に、フィボナッチヒープは \(\textsc{Insert}\), \(\textsc{ExtractMin}\), \(\textsc{DecreaseKey}\) の操作をサポートします。しかしこれら全ての操作に \(O(\log n)\) 時間がかかる二分ヒープと違って、フィボナッチヒープは \(\textsc{Insert}\) と \(\textsc{DecreaseKey}\) 操作をならし \(O(1)\) 時間で行えます。ただし \(\textsc{ExtractMin}\) のならし実行時間は \(O(\log n)\) のままです1。
この高速なデータ構造を利用するには、\(G\) の辺ではなく頂点を優先度付きキューに保存する必要があります。ここで頂点 \(v\) の優先度は \(v\) と \(T\) の頂点を結ぶ辺の重みであり、そのような辺が無ければ \(\infty\) です。アルゴリズムの最初で全ての頂点を優先度付きキューに入れておき、\(T\) に新しい辺が加わるたびにその辺に隣接する辺の優先度を小さい値に更新します。
説明を簡単にするために、アルゴリズムを二つに分けます。\(\textsc{JarníkInit}\) が優先度付きキューを初期化し、\(\textsc{JarníkLoop}\) がメインの処理を行います。入力はグラフの頂点と辺、そして開始頂点 \(s\) です。アルゴリズムの実行中、各頂点 \(v\) に対して二つの値が割り当てられます。一つは \(v\) の優先度 \(\mathit{priority}(v)\) で、もう一つは \(w(\mathit{edge}(v)) = \mathit{priority}(v)\) が成り立つような \(v\) に隣接する辺 \(\mathit{edge}(v)\) です。
procedure \(\texttt{Jarník}\)(\(V, E, s\))
\(\texttt{JarníkInit}\)(\(V, E, s\))
\(\texttt{JarníkLoop}\)(\(V, E, s\))
procedure \(\texttt{JarníkInit}\)(\(V, E, s\))
for \(v \in V \backslash \lbrace s \rbrace\) do
if \(vs \in E\) then
\(\mathit{edge}(v) \leftarrow vs\)
\(\mathit{priority}(v) \leftarrow w(vs)\)
else
\(\mathit{edge}(v) \leftarrow \textsc{Null}\)
\(\mathit{priority}(v) \leftarrow \infty\)
\(\texttt{Insert}\)(\(v\))
procedure \(\texttt{JarníkLoop}\)(\(V, E, s\))
\(T \leftarrow (\lbrace s \rbrace, \varnothing)\)
for \(i \leftarrow 1\) to \(|V| - 1\) do
\(v \leftarrow\)\(\texttt{ExtractMin}\)()
\(v\) と \(\mathit{edge}(v)\) を \(T\) に加える
for \(v\) に隣接する頂点 \(u\) do
if \(u \notin T \text{ かつ } \mathit{priority}(u) > w(uv)\) then
\(\mathit{edge}(u) \leftarrow uv\)
\(\texttt{DecreaseKey}\)(\(u, w(uv)\))
\(\textsc{Insert}\) と \(\textsc{ExtractMin}\) は \(s\) 以外の頂点に対して一回ずつ、合計で \(O(V)\) 回呼ばれ、\(\textsc{DecreaseKey}\) は全ての辺に対して最大二回、合計で \(O(E)\) 回呼ばれます。よってフィボナッチヒープを使って改善したアルゴリズムの実行時間は \(\pmb{O(E + V \log V)}\) です。これは \(E = O(V)\) の場合を除いて Borůvka のアルゴリズムよりも高速です。
しかし実際のデータに対してこのアルゴリズムを動かした場合、フィボナッチヒープを使った実装が二分ヒープを使ったナイーブな実装よりも早くなるためには、グラフが極端に巨大かつ密である必要があります。フィボナッチヒープのアルゴリズムはかなり複雑なので、漸近表記に隠されている定数部分が大きいためです ――常軌を逸したほど巨大であるとは言いませんが、二分ヒープの操作の実行時間を表す \(O(\log n)\) という表記に隠れている定数部分よりは明らかに大きいです。
-
ならし時間 (amortized time) とはデータ構造の操作において稀に起きる実行時間の変動を無視するための集計上のトリックです。フィボナッチヒープは \(I\) 個の \(\textsc{Insert}\), \(D\) 個の \(\textsc{DecreaseKey}\), \(X\) 個の \(\textsc{ExtractMin}\) を任意に入れ替えた操作列を最悪ケースでも \(O(I+D+X\log n)\) 時間で行えます。ただし、一つ一つの操作の最悪ケースにおける実行時間はこれを平均したものよりも長くなることがあります。 ならし時間の解析で使っているのは操作列の実行時間に対する統計的な平均であり、入力データやアルゴリズムのランダム性は仮定されていません。[return]