ペナントレースにおける敗退

毎年何百万人という野球ファンが熱心に試合を観戦し、贔屓チームがプレーオフそしてワールドシリーズに進むことを期待します。しかし非情なことに、シーズンが終わる数日前あるいは数週間前の時点で、ほとんどのチームはペナントレースから "数学的に" 敗退します。通常はあるチームが敗退したかどうかを判断するのは簡単です ――現在地区トップのチームに追いつけるほど試合数が無ければ敗退です―― が、状況がもっと複雑になることもあります。次に示すのは 1996 年 8月 30 日のアメリカンリーグ東地区で実際に起こった順位です: \[ \begin{array}{ccc|ccccc} \hline \text{チーム} & \text{勝-敗} & \text{残り試合数} & \text{NYY} & \text{BAL} & \text{BOS} & \text{TOR} & \text{DET} \\ \hline \text{New York Yankees} & 75-59 & 28 & & 3 & 8 & 7 & 3 \\ \text{Boltimore Orioles} & 71-63 & 28 & 3 & & 2 & 7 & 4 \\ \text{Boston Red Sox} & 69-66 & 27 & 8 & 2 & & 0 & 0 \\ \text{Toronto Blue Jays} & 63-72 & 27 & 7 & 7 & 0 & & 0 \\ \text{Detroit Tigers} & 49-86 & 27 & 3 & 4 & 0 & 0 & \\ \hline \end{array} \] 明らかに Detroit は後れを取っていますが、それでも粘り強いファンは希望を捨てていませんでした。もし Detroit が残りの 27 試合に全て勝利すれば合計で 76 勝となって現在のどのチームよりも勝利数が多くなるからです。その上で他のチームが全ての試合に敗北すれば...。

しかし他のチームもお互いに試合をしなければならないので、これは不可能です。理由を完全に説明すると次のようになります¹:

残りの試合全ての勝利することで、Detroit はシーズンを 76 勝 86 敗という成績でシーズンを終えることができる。しかし Yankees が 2 試合でも勝利すれば 77 勝 85 敗となって Detroit を上回る成績となる。よって Tigers が一度も負けずに、Yankees が一度も勝てずにシーズンが終わると仮定する。

このシナリオにおける問題は、New York が Boston との試合を 8 試合残しているという点にある。Red Sox がそれらの試合に全て勝利した場合、77 勝以上が確定して Tigers よりも良い成績となってしまう。よって Detroit が一位となる可能性を消さないためには、New York が Boston との 8 試合のうちちょうど \(1\) 試合だけ勝利し、他の試合に敗北する必要がある。一方で Sox は New York 以外との全ての試合において敗北しなければならない。以上の条件が成り立てば、Detroit と New York と Red Sox が同着一位となる ...。

このシナリオにおいて Orioles と Blue Jays で何が起こるかを見よう。Baltimore は Boston と 2 試合、New York と 3 試合が残っているので、上記のようにことが進んだ場合には Baltimore は最低でも 76 勝でシーズンを終えることになる。よって Detroit が Baltimore に抜かされないためには、Baltimore は New York と Boston 以外の全ての試合に敗北しなければならない。つまり、Baltimore は Totonto との残り 7 試合全てに敗北しなければならない。一方で Blue Jays は Yankees との試合も 7 試合残っており、既に見た通り Detroit が一位となるためにはこの試合は全て Blue Jays が勝利する必要がある。しかしそうなると Blue Jays は現在の状況から 14 試合に勝利することになり、最終成績が 77 勝となって Detroit を抜いて一位となってしまう。したがって、これから何が起ころうとこのシーズンにおいて Detroit がアメリカンリーグ東地区で一位になることは不可能である。

もっと簡単にこれを示す方法があるはずです！

この問題を抽象的に定式化するとこうなります: 入力は二つの配列 \(W[1..n]\) と \(G[1..n,1..n]\) であり、\(W[i]\) がチーム \(i\) の現在の勝利数を表し、\(G[i,j]\) がチーム \(i\) とチーム \(j\) の残り試合数を表します。出力はチーム \(n\) が最多の勝利数でシーズンを終えることができるかどうかです (同着一位でも良いとします)²。

1960 年代の中頃、Benjamin Schwartz (ベンジャミン・シュワルツ) はこの問題が最大フローを使ってモデル化できることを示しました。それから約 20 年後、Dan Gusfield (ダン・ガスフィールド)、Charles Martel (チャールズ・マーテル)、David Fernández-Baca (デイビッド・フランシス・バカ) は Schwartz のフローによる定式化を組選択問題に単純化しました。つまり、チーム \(n\) が一位となるための各ゲームにおける勝者を選択するということです。\(R[i] = \sum_{j} G[i,j]\) をチーム \(i\) の残り試合数とし、これ以降はチーム \(n\) が残りの \(R[n]\) 試合に全て勝利すると仮定します。この仮定の下でチーム \(n\) が一位になれるのは、他の全てのチーム \(i\) について、残り \(R[i]\) 試合における勝利数が \(W[n] + R[n] - W[i]\) 以下であるときだけです。

各試合で勝利するチームを選択することから、頂点が試合とチームを表す二部グラフを構築します。試合を表す \(\binom{n}{2}\) 個の頂点 \(g_{i, j}\) \((1 \leq i < j < n)\) とチームを表す頂点 \(t_{i}\) \((1 \leq i < n)\) を考え、全ての添え字の組 \((i,j)\) について、容量が無限大の \(g_{i,j} \rightarrow t_{j}\) と \(g_{i,j} \rightarrow t_{i}\) という辺を追加します。さらにソース頂点 \(s\) と各組 \((i,j)\) に対する容量 \(G[i,j]\) の辺 \(s \rightarrow g_{i,j}\) を追加し、シンク頂点 \(t\) と各チーム \(i\) に対する容量 \(W[n] + R[n] - W[i]\) の辺 \(t_{i} \rightarrow t\) も加えます。

1996年のアメリカンリーグ東地区に対するグラフを次に示します。チーム \(n\) は Detroit Tigers で、ラベルの付いていない辺は無限大の容量を持ちます。

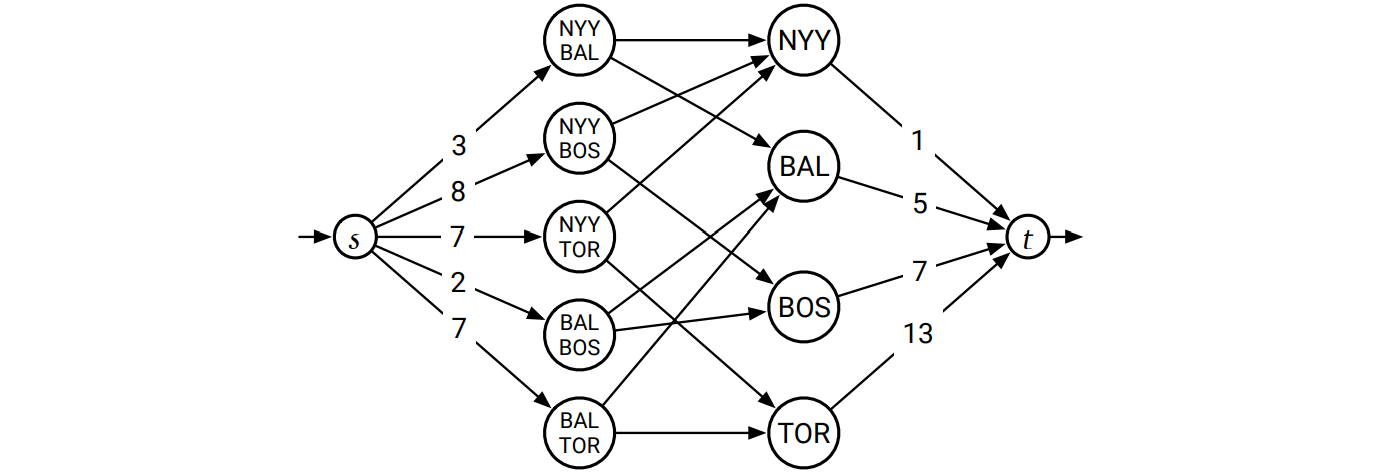
定理チーム \(n\) が一位でシーズンを終えられることは、\(s\) から出る全ての辺を飽和させる実現可能なフローが存在することと同値。

証明チーム \(n\) が一位でシーズンを終えられるとする。このとき他の全てのチーム \(i < n\) の残り試合における勝利数は最大でも \(W[n] + R[n] - W[i]\) である。チーム \(n\) が一位となるシナリオにおいて、\(i\) と \(j\) が戦って \(k \in \lbrace i, j \rbrace\) が勝つような試合ごとに有向路 \(s \rightarrow g_{i,j} \rightarrow t_{k} \rightarrow t\) に沿って一単位のフローを流していく。\(i\) と \(j\) の間の試合は \(G[i,j]\) 回行われるので、こうして出来上がるフローは \(s\) から出る全ての辺を飽和させる。また各チーム \(i\) の勝利数は最大でも \(W[n] + R[n] - W[i]\) だから、こうして出来上がるフローは実現可能である。

逆に \(s\) から出る全ての辺を飽和させる実現可能なフロー \(f\) が存在するとする。このとき全ての \((i,j)\) の組について、チーム \(i\) がチーム \(j\) との試合に \(f(g_{i,j} \rightarrow t_{i})\) 回勝つとする。このとき \(i\) と \(j\) の間の試合は \(f(g_{i,j} \rightarrow t_{i}) + f(g_{i,j} \rightarrow t_{j})\) \(= f(s \rightarrow g_{i,j}) = G[i,j]\) 回行われるので、全ての試合が終わっている。また \(i\) が試合に勝つのは \(\sum_{j} f(g_{i,j} \rightarrow t_{i}) = \) \(f(t_{i} \rightarrow t) \leq \) \(W[n] + R[n] - W[i]\) 回なので、シーズン累計の勝利数は \(W[n] + R[n]\) 回以下である。したがってチーム \(n\) が残りの試合全てに勝つならば \(n\) は一位でシーズンを終えられる。 \(\Box\)

好きなチームが勝つかどうかを判定する方法をまとめると、まずフローネットワークを構築し、最大フローを計算し、その最大フローが \(s\) から出る辺を全て飽和させるかどうかを見ればよいということになります。例えば上記のグラフでは \(s\) から出る辺の容量の和は (Detroit が関わらない残り試合数と等しい) 27 ですが、\(t\) へ向かう辺の容量の和は 26 しかありません。つまり最大フローの値は 26 以下にしかなれず、Detroit は数学的に敗退していると結論できます³。

フローネットワークは \(O(n^{2})\) 個の頂点と \(O(n^{2})\) 個の辺を持ち、\(O(n^{2})\) 時間で構築できます。よって Orlin のアルゴリズムを使えば最大フローを \(O(VE) = \pmb{O(n^{4})}\) 時間で計算可能です。

このアルゴリズムはペナントレースの敗退問題に対する最速のアルゴリズムではありません。2001 年、Kevin Wayne (ケビン・ウェイン) は数学的に敗退する全てのチームをわずか \(\pmb{O(n^{3})}\) 時間で見つけるアルゴリズムを発見しました。突き詰めればこのアルゴリズムも最大フローの計算を一度だけ使っています。

この例とその説明は、Eli V. Olinick のウェブサイト https://s2.smu.edu/~olinick/riot/detroit.html からです。このページは Olinick が Ilan Adler, Alan Erera, Dorit Hochbaum と共に行った共同研究に基づいています。^[return]
試合が引き分けになることはなく、試合が中止になることもないとします。メジャーリーグではプレーオフ進出がかかった試合およびその他のほとんどの試合で引き分けはありませんが、レギュラーシーズンでは (戦争、自然災害、ハチの群れなどが原因で) 試合が中止になることがあります。^[return]
この例ではラッキーでした。\(t\) へ向かう辺の容量の和が \(s\) から出る辺の容量の和よりも大きいにもかかわらずチーム \(n\) が敗退しているという状況はあり得ます。^[return]