データ構造

実際のプログラムでグラフを扱うときは、たいていは隣接リストと隣接行列という二つのよく知られたデータ構造のどちらかを使ってグラフを表現することになります。高いレベルで抽象的に言うと、どちらのデータ構造も頂点を添え字とした配列です。各頂点に \(1\) から \(V\) のユニークな整数を割り当てて、この整数と頂点を同一視します。

隣接リスト

グラフの格納に使われる最も一般的なデータ構造は隣接リスト (adjacency list) です。隣接リストはリストの配列であり、配列の各要素が一つの頂点に隣接する全ての頂点 (有向グラフの場合は出隣接点1) を保持します。無向グラフでは、全ての辺 \(uv\) は隣接リストに二度格納されます: 一度は \(u\) の隣接リストに、もう一度は \(v\) の隣接リストに格納されるからです。これに対して無向グラフでは、辺 \(u \rightarrow v\) はその尾 \(u\) の隣接リストに一度だけ格納されます。無向グラフと有向グラフの両方において、隣接リストに必要になる空間量は \(O(V+E)\) です。

隣接リストを表現する方法はいくつかありますが、通常の実装は一重連結リストを使います。こうした場合、\(v\) の隣接リストをたどることで、頂点 \(v\) に隣接する頂点を \(O(1 + \deg (v))\) 時間で列挙できます。同様に \(u \rightarrow v\) が辺かどうかは、\(u\) の隣接リストをたどることで \(O(1 + \deg (u))\) 時間で判定できます。無向グラフでは、この時間を \(O(1 + \min \lbrace \deg (u), \deg (v) \rbrace)\) にできます: \(u\) と \(v\) の隣接リストを同時にたどれば、目的の辺またはどちらかの終端までたどるだけで済むからです。

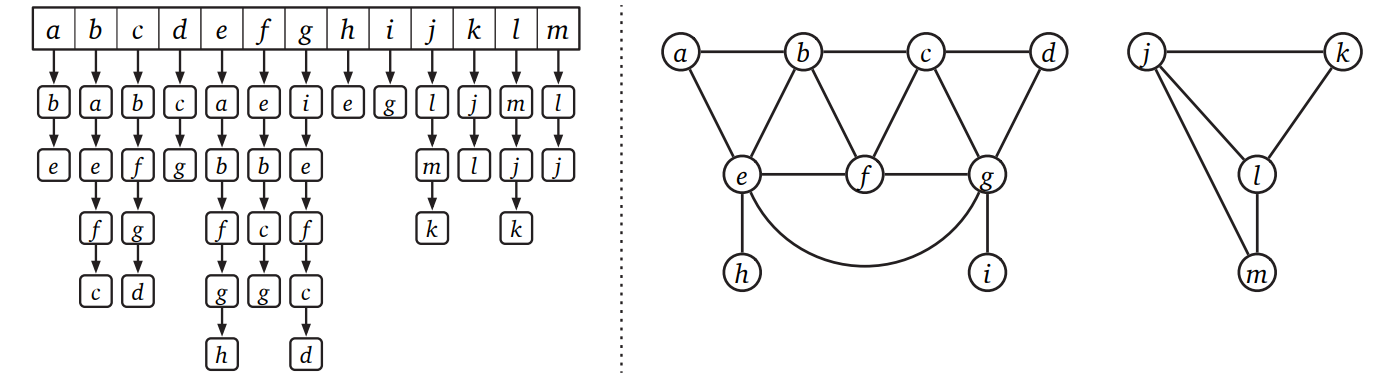
例のグラフに対する隣接リスト
図 5.9
例のグラフに対する隣接リスト

もちろん、隣接リストの実装に使うことができるデータ構造が連結リストだけであるというわけではありません。探索、列挙、挿入、削除をサポートするデータ構造であれば何でも使うことができます。例えばバランスの取れた二分探索木を使って \(u\) の隣接頂点を格納すれば、 \(uv\) が辺かどうかを判定するのにかかる時間を \(O(1 + \log(\deg(u)))\) に削減できます。あるいは適切に構築されたハッシュテーブルを使って、探索を \(O(1)\) 時間にすることだってできます2。

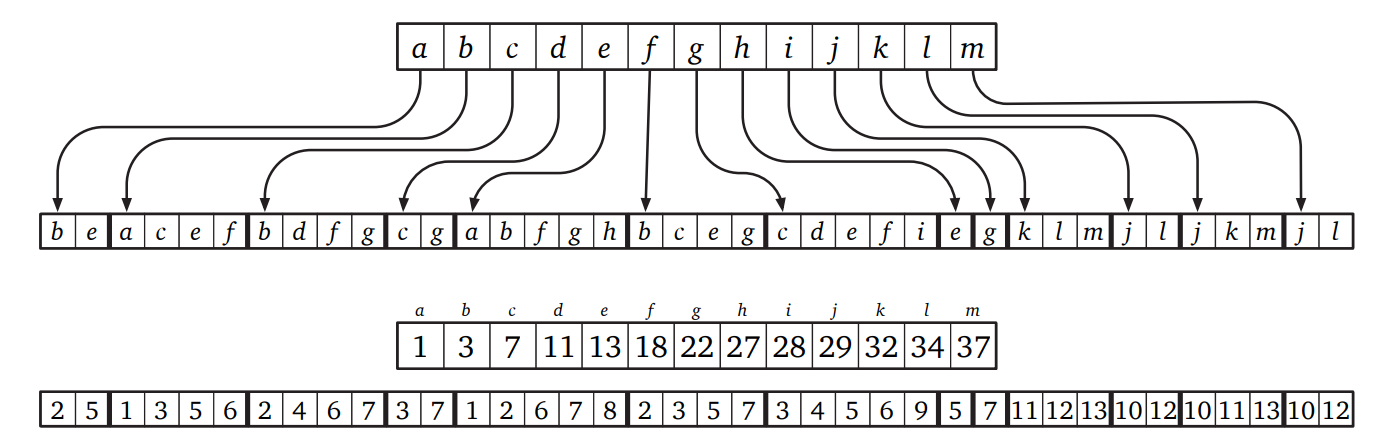
もう一つのよく使われる隣接リストの実装は隣接配列 (adjacency array) です。一つの配列 (図中下) には全ての辺が格納され、ある頂点を始点とする辺の集合が連続する部分列で表されます。そしてもう一つの配列 (図中上) には各頂点に対応する一つ目の配列の部分列が始まる場所が格納されます。加えて下の図に示すように各頂点に対応する部分配列をソートした状態に保っておくと、 \(u\) と \(v\) が隣接しているかどうかを \(O(\log \deg (u))\) 時間で判定できます。

例のグラフに対する抽象的な隣接配列と、配列の組を使った実際の実装
図 5.10
例のグラフに対する抽象的な隣接配列と、配列の組を使った実際の実装

隣接行列

グラフを表現するもう一つのよく知られたデータ構造は隣接行列 (adjacency matrix) です。1894年に George Burunel (ジョージ・ブルーネル) によって最初に提案されました。グラフ \(G\) の隣接行列とは要素が \(0\) と \(1\) からなる \(V \times V\) の行列で、通常は二次元配列 \(A[1..V, 1..V]\) によって表されます。隣接行列の各要素は辺に対応し、その辺が \(G\) に存在するかどうかを表します:

例のグラフに対する隣接行列

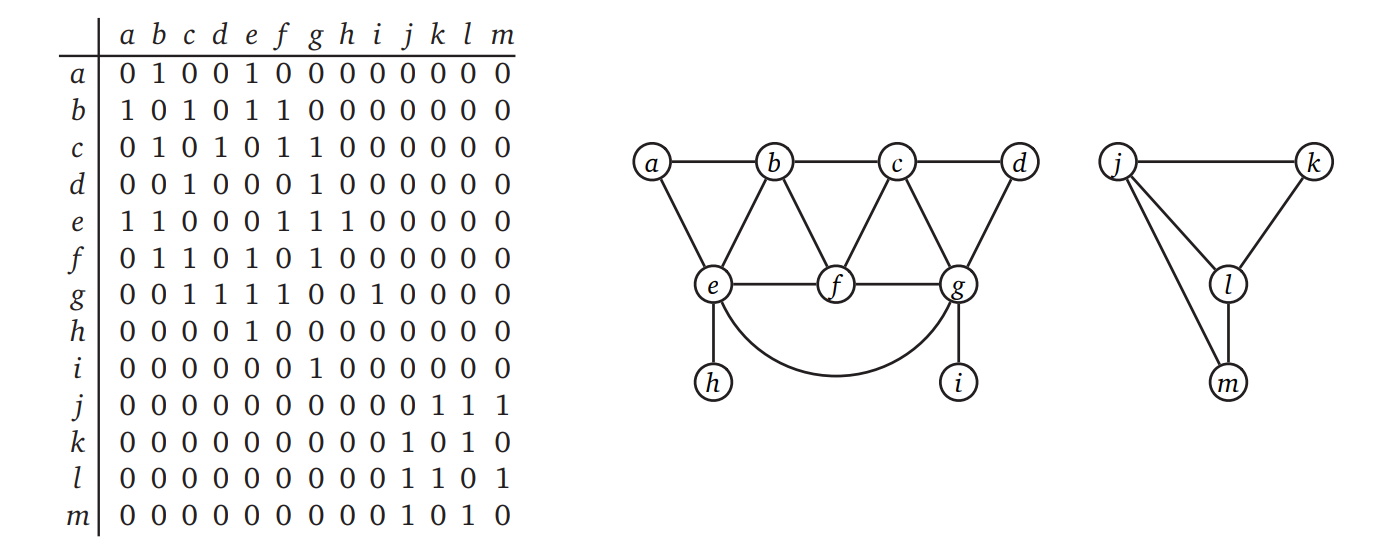
無向グラフでは \(uv\) と \(vu\) は同じ辺に対する違う名前にすぎないので、任意の \(u, v\) に対して \(A[u,v] = A[v,u]\) であり、隣接行列は必ず対称です。また無向グラフの対角要素 \(A[u,u]\) は全て \(0\) です。これに対して有向グラフに対する隣接行列は対称でないこともあり、対角要素も \(0\) だとは限りません。

隣接行列が与えられたとき、二つの頂点が辺で結ばれているかの判定は \(\Theta(1)\) 時間で行えます。行列の対応する要素を調べるだけで済むからです。またある頂点に隣接する頂点の列挙は、対応する行 (または列) を走査することで \(\Theta(V)\) 時間で行えます。この実行時間は最悪ケースでは最適ですが、頂点に隣接する頂点が少ししか無いときにも列全体を走査する必要があります。同様に、隣接行列はグラフに含まれる辺の数に関わらず \(\Theta(V^{2})\) の空間を必要とします。このため隣接行列は密なグラフを表すときの空間効率に優れています。

比較

基本的なグラフデータ構造のパフォーマンスを次の表にまとめます。星印 \({}^{\ast}\) は動的ハッシュテーブルを使った場合の期待償却計算時間 (expected amortized time3)を示します。 \[ \footnotesize \begin{array}{c|ccc} & \text{標準的な隣接リスト} & \text{高速な隣接リスト} & \text{隣接行列} \\ & \text{(連結リスト)} & \text{(ハッシュテーブル)} & \\ \hline \text{空間} & \Theta(V + E) & \Theta(V + E) & \Theta(V^{2}) \\ \hdashline uv \in E \text{ の判定} & O(1 + \min \lbrace \deg(u),\ \deg(v) \rbrace) = O(V) & O(1) & O(1) \\ u \rightarrow v \in E \text{ の判定} & O(1 + \deg(u)) = O(V) & O(1) & O(1) \\ v \text{ の隣接頂点の列挙} & \Theta(1 + \deg(v)) = O(V) & \Theta(1 + \deg(v)) = O(V) & O(V) \\ \text{全ての辺の列挙} & \Theta(V + E) & \Theta(V+E) & \Theta(V^{2}) \\ \text{辺 } uv \text{ の追加} & O(1) & O(1)^{\ast} & O(1) \\ \text{辺 } uv \text{ の削除} & O(\deg(u) + \deg(v)) = O(V) & O(1)^{\ast} & O(1) \end{array} \]

時間効率にも空間効率にも劣る隣接行列を使おうとする人がいるのか、というのはこの比較を見たときに生じるもっともな疑問です。隣接行列を使う一番の理由は、十分に密なグラフに対しては隣接行列を使った方がより単純でかつ実際の効率も良いからです。隣接行列にはポインタを使った間接参照やハッシュ関数によるオーバーヘッドが無く、連続したメモリ領域を処理できます。

同様に、二分探索木やハッシュテーブルではなくて連結リストを使って隣接リスト構造を実装する人がいるのか、というのももっともな疑問です。実際にプログラムを書く人の最初の答えはまず間違いなく「みんなそうしてるから」 ――Donald Knuth のコードで問題なかったのなら、自分のコードで使っても問題ないに違いない！―― ですが、もう少しきちんとした議論もできます。一つ目の理由は、ほとんどのアプリケーションでは連結リストを使った普通の隣接リストで十分なことです。大多数の標準的なグラフアルゴリズムにおいては、特定の辺が存在するかどうかを判定したり、辺の追加/削除したりすることが全く (あるいはほとんど) ありません。そのためそういった操作を高速化するためのデータ構造は不必要です。

しかし私の意見では、二つの標準的なデータ構造を使う最も説得力ある理由は「多くのグラフが隣接行列または標準的な隣接リストを暗黙のうちに定義するから」です。例えば:

最後の二つの例では任意の頂点から出る辺をその頂点の次数に比例する時間で列挙できますが、二つの頂点の間に辺があるかを定数時間で求めることは必ずしも可能とは限りません (「このレコードからあのレコードの間へ向かうポインタはあるか？」あるいは「この構成からあの構成に一手で行けるか？」)。さらに、レコードのポインタの整理やゲーム構成の定義の変更によってデータ構造の効率を改善することは通常できません。このような理由により、隣り合う頂点を連結リストに収めた標準的な連結リストがこの種のデータ構造を表現するのに適しています。

この本ではこの先、明示的にそうでないと書く場合を除いて、グラフアルゴリズムの実行時間の解析は入力グラフが標準的な (連結リストを使った) 隣接リストで表されていることを仮定して行います。同様に、明示的に書く場合を除いて、練習問題でアルゴリズムを説明、解析するときには入力グラフが標準的な隣接リストで表されていると仮定してください。

  1. 細かいことに目が行く学生は、隣接リストが本当はリストでないことに気が付くかもしれません。この命名は薫製ニシンの虚偽の例といえます: 情報科学では、数学と同じように、赤いニシン (red herring) が赤い必要はありませんし、魚である必要もありません。[return]

  2. これを実際に行うには想像よりもはるかに微妙な技法が必要になります。よく知られたハッシュ技法のほとんどは高速なクエリ時間を保証しておらず、良いとされるハッシュ法でも \(O(1)\) 時間の期待値を持つにすぎないものが多くあるからです。ハッシュに関する議論は http://algorithms.wtf/ を参照してください。[return]

  3. "expected amortized" の意味が分からなくても気にしないでください。[return]

広告
このページの文章はテキストゆれないくんを使って校正されました。