最長増加部分列

前の章で考えた問題の中に、与えられた数値の配列 \(A[1..n]\) に含まれる一番長い増加部分列の長さを求めるという問題があり、この問題に対するバックトラッキングを使ったアルゴリズムを二つ説明しました。どちらも最悪ケースの実行時間が \(O(2^{n})\) でしたが、両方とも動的計画法を使うことで著しい高速化が可能です。

一つ目の再帰方程式: これは次？

一つ目のバックトラッキングを使ったアルゴリズムが評価するのは、全ての要素が \(A[i]\) よりも大きい \(A[j..n]\) の増加部分列で一番長いものの長さを返す関数 \(\mathit{LISBigger}(i, j)\) です。この関数に対しては次の再帰方程式が成り立っていました: \[ \mathit{LISBigger}(i, j) = \begin{cases} 0 & \text{if } j > n \\ \mathit{LISBigger}(i, j + 1) & \text{if } A[i] \geq A[j] \\ \max \left\lbrace \begin{array}{c} \mathit{LISBigger} (i, j + 1) \\ 1 + \mathit{LISBigger}(j, j + 1) \end{array} \right\rbrace & \text{それ以外} \end{cases} \] 元の問題を解くには、門番 \(A[0] = -\infty\) を入力配列に追加した上で \(\mathit{LISBigger}(0, 1)\) を計算します。

再帰的に登場する小問題は二つの添え字 \((i, j)\) で特定できます。したがって考えるべき異なる小問題は \(O(n^{2})\) 個だけであり、この小問題の結果は二次元配列 \(\mathit{LISBigger}[0..n, 1..n]\) に格納できます¹。さらに、再帰呼び出しを無視した場合の小問題は \(O(1)\) 時間で解けるので、最終的に出来上がる動的計画法を使うアルゴリズムの実行時間は \(O(n^{2})\) になると予想できます。

この再帰的なアルゴリズムをメモ化を使うように書き換えたとして、そのアルゴリズムが配列を埋める順番は今までの例ほど明らかではありません。再帰方程式を見て分かるのは、\(\mathit{LISBigger}[i, j]\) が埋まるのが次の列の \(\mathit{LISBigger}[i, j + 1]\) と \(\mathit{LISBigger}[j, j + 1]\) が埋まった後だということです。次の図の左側にこれを示します。

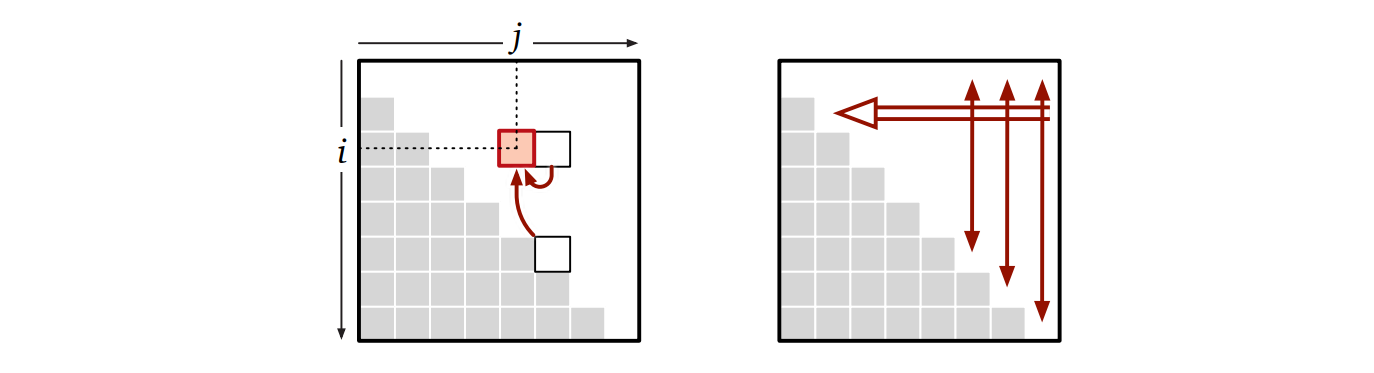
幸いにも、この部分的な情報さえあれば破綻しない評価順序を得ることができます。つまり、一列ごとに右から左へ埋めていけば、あるマスの値を埋めるときにはその値が依存している値が全て求まっているということが言えます。この順序は再帰的なアルゴリズムが表を埋めるの順序と同じではないかもしれませんが、正しく動くので、使えます。上図の右側にこの評価順序を図示します。二重の矢印が外側のループを、一重の矢印が内側のループを表します。一重の矢印が両方向を向いているのは、列の中の値を埋める順番が重要でないためです。

そして、これで終わりです！ 以上の説明から得られる動的計画法を使ったアルゴリズムの疑似コードを次に示します:

このアルゴリズムが予想通り \(O(n^{2})\) 時間で実行できることはすぐに分かります。もし必要なら、使用する表の列を \(\mathit{LISBigger}[\cdot, j]\) と \(\mathit{LISBigger}[\cdot, j+1]\) という一番新しい二列だけにして、空間消費量を \(O(n^{2})\) から \(O(n)\) に落とすことができます²。

二つ目の再帰方程式: 次は何？

最長増加部分列問題を解く二つ目のバックトラッキングアルゴリズムが評価するのは、\(A[i]\) から始まる \(A[i..n]\) の増加部分列のうち一番長いものの長さを返す関数 \(\mathit{LISFirst(i)}\) です。この関数に対しては次の再帰方程式が成り立っていました: \[ \mathit{LISFirst}(i) = 1 + \max \lbrace \mathit{LISFirst}(j)\ |\ j > i \text{ かつ } A[j] > A[i] \rbrace \] ここでベースケース \(\mathit{LISFirst}(n) = 1\) が簡単に満たされるように \(\max \varnothing = 0\) と定義されます。元の問題を解くには、門番 \(A[0] = -\infty\) を入力配列に追加した上で \(\mathit{LISFirst}(0) - 1\) を計算します。

この場合では再帰的な小問題は一つの添え字 \(i\) を使って特定できるので、再帰方程式の計算結果は一次元配列 \(\mathit{LISFirst}[1..n]\) に格納できます。この配列の要素 \(\mathit{LISFirst}[i]\) は \(j > i\) を満たす \(\mathit{LISFirst}[j]\) に依存しているので、配列を降順に埋めていくことになります。 \(\mathit{LISFirst}[i]\) を計算するには \(j > i\) を満たす全ての添え字 \(j\) に対する \(\mathit{LISFirst}[j]\) が必要になりますが、\(j\) を考える順番はどんなものでも構いません。最終的に出来上がる動的計画法を使ったアルゴリズムの実行時間は \(O(n^{2})\) で、消費空間は \(O(n)\) です:

1. \(i < j\) が必ず成り立つので、本当はこの配列の半分しか必要になりません。定数時間の高速化についてはこの本で扱いませんが、仮に高速化を行うにしても、このタイミングで配列のサイズを削ることを考えるのは時期尚早です。「まず動くようにせよ。それから速くせよ」^[return]

2. 言ったでしょう、定数部分は気にするなって！^[return]