N クイーン
バックトラッキングを使うアルゴリズムとして分かりやすいのが、有名な \(\pmb n\) クイーン問題を解くアルゴリズムです。通常の 8 x 8 のチェス盤に対するこの問題はドイツ人チェス愛好家 Max Bezzel (マックス・ベッツェル) によって ("Schachfreund" という偽名で) 1848 年に発表され、1869 年には一般的な \(n \times n\) の盤に対する問題が François-Joseph Eustache Lionnet (フランソワ=ジョゼフ・ウスターシュ・ライオネット) によって提案されました。
\(n\) クイーン問題とは、\(n \times n\) のチェス盤に \(n\) 個のクイーンをお互いを攻撃できないように置くという問題です。チェスを知らない読者のために言っておくと、クイーンがお互いを攻撃できないとは、どのクイーンも同じ列、行、対角線上に無いことを意味します。
![配列 [4, 7, 3, 8, 2, 5, 1, 6] によって表される、8 クイーン問題への解の一つ (Gauss が最初に示したもの)](/algorithms/AlgorithmFigure_2-1.png)
著名な数学者 Carl Friedrich Gauss (カール・フリードリヒ・ガウス) は 1850 年に友人 Heinrich Schumacher (ハインリッヒ・シューマッハ) へ書いた手紙の中で、Franz Nauck (フランツ・ナウク) によって発見された 8 クイーン問題が 92 個の答えを持つという事実は、数時間試行錯誤を繰り返せば簡単に確認できると記しています (Schwer ist es übrigens nicht, durch ein methodisches Tatonnieren sich diese Gewissheit zu verschaffen, wenn man eine oder ein paar Stunden daran wenden will.)。彼の用いた Tatonniren という言葉は、周りが見えない暗闇の中で周りの様子を手探りで確かめるという意味のフランス語 tâtonner から来ています。
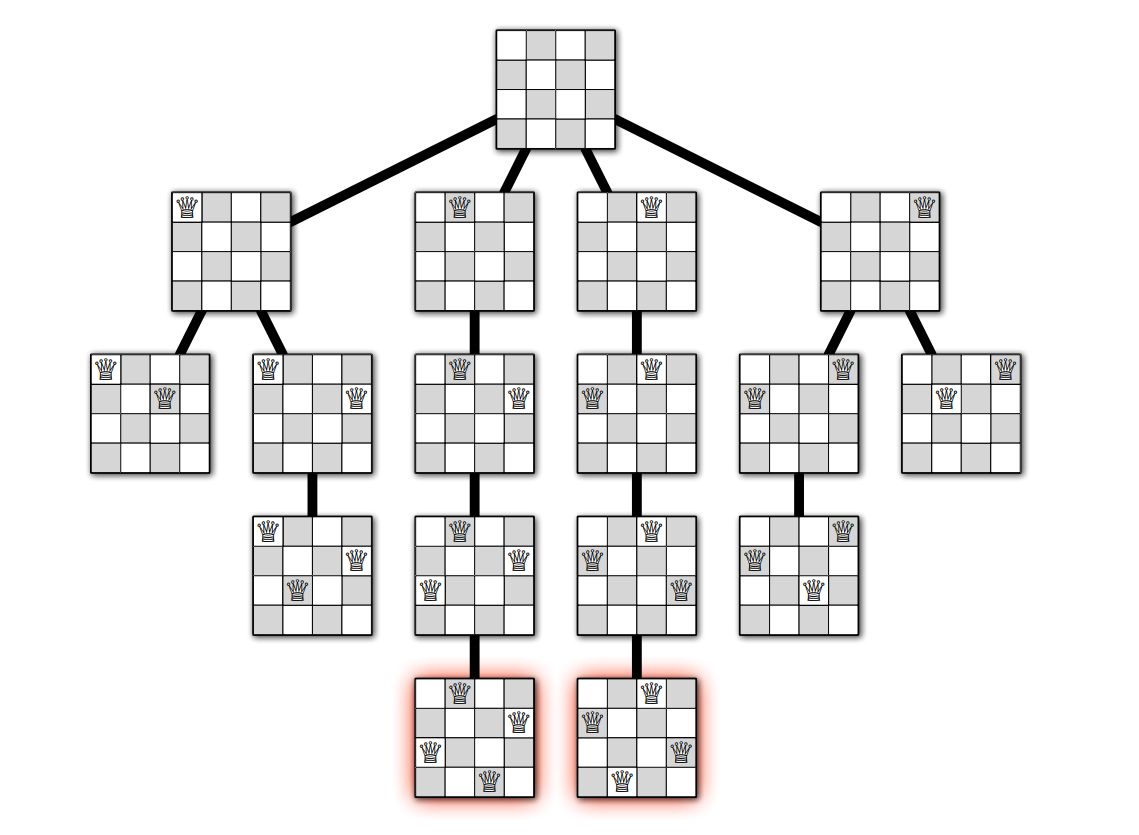
Gauss がこの手紙で説明した解法を紹介します。同じ解法はフランス人娯楽数学者 Édouard Lucas (エドゥアール・リュカ) も 1882 年に発表しており、Lucas はこの解法を Emmanuel Laquière (エマニュエル・ラキエ) から得たとしています。\(n\) クイーン問題の条件を満たすクイーンの配置を配列 \(Q[1..n]\) で表すことにします。ここで \(Q[i]\) は \(i\) 列におけるクイーンの場所を表します。こうすれば、クイーンを一番上の列から列ごとにひとつずつ盤に置いていくという再帰的な戦略で解を求めることができます。具体的には、\(r\) 番目のクイーンを置くときに盤の \(r\) 列目にある \(n\) 個のマスを単純な for ループで調べ、もしあるマスがそれまでに置いたクイーンによって攻撃されるなら、そのマスは無視します。そうでなければ、そのマスにクイーンを暫定的に配置し、他のクイーンを以降の列に配置できるかどうかを再帰的に調べます。
アルゴリズム全体を次に示します。このアルゴリズムは途中まで完了したクイーンの配置を受け取り、その配置と矛盾しない \(n\) クイーン問題の解を全て枚挙します。 入力 \(r\) は次にクイーンを置く列の添え字であり、\(Q[1..r-1]\) は最初の \(r - 1\) 個のクイーンの配置です。\(\textsc{PlaceQueens}(Q[1..n], 1)\) を呼べば追加の制約がない \(n\) クイーン問題の解を全ての枚挙できます。外側の for ループが \(r\) 列におけるクイーンの配置を走査し、内側の for ループが \(r\) 列へのその配置がこれまでに配置された \(r - 1\) 個のクイーンから攻撃されるかどうかを調べます。
procedure \(\texttt{PlaceQueens}\)(\(Q[1..n], r\))
if \(r = n + 1\) then
print \(Q\)
else
for \(j \leftarrow 1\) to \(n\) do
\(\mathit{legal} \leftarrow \textsc{True}\)
for \( i \leftarrow 1\) to \(r - 1\) do
if \((Q[i] = j)\) or \((Q[i] = j + r - 1)\) or \((Q[i] = j - r + i)\) then
\(\mathit{legal} \leftarrow \textsc{False}\)
if \( \mathit{legal} \) then
\(Q[r] \leftarrow j\)
\(\texttt{PlaceQueens}\)(\(Q[1..n], r + 1\))
\(\textsc{PlaceQueens}\) の実行は再帰木 (recursion tree) を使って可視化できます。再帰木の頂点は再帰的に呼ばれる小問題に対応し、このアルゴリズムでは制約を満たす部分解を表します。再帰木の根は何も配置されていない盤 (\(r = 0\)) を、辺は再帰呼び出しを、葉はクイーンをそれ以上配置できない部分解を表します。クイーンが配置できない理由は全ての列にクイーンが配置されているためか、そうでなければ空の列の全てのマスがそれまでに配置されたクイーンから攻撃されるためです。バックトラッキングを使った完全な解の探索はこの木に対する深さ優先探索と同じ動きをします。