バックトラッキング

この章ではバックトラッキング (backtracking) と呼ばれるもう一つの重要な再帰的戦略を説明します。バックトラッキングを使うアルゴリズムは計算問題に対する答えを少しずつ構築します。答えとして次に追加する要素の選択肢が複数ある場合には、全ての選択肢を再帰的に評価し、一番良いものを選択します。

N クイーン

バックトラッキングを使うアルゴリズムとして分かりやすいのが、有名な \(\pmb n\) クイーン問題を解くアルゴリズムです。通常の 8 x 8 のチェス盤に対するこの問題はドイツ人チェス愛好家 Max Bezzel (マックス・ベッツェル) によって ("Schachfreund" という偽名で) 1848 年に発表され、1869 年には一般的な \(n \times n\) の盤に対する問題が François-Joseph Eustache Lionnet (フランソワ=ジョゼフ・ウスターシュ・ライオネット) によって提案されました。

\(n\) クイーン問題とは、\(n \times n\) のチェス盤に \(n\) 個のクイーンをお互いを攻撃できないように置くという問題です。チェスを知らない読者のために言っておくと、クイーンがお互いを攻撃できないとは、どのクイーンも同じ列、行、対角線上に無いことを意味します。

著名な数学者 Carl Friedrich Gauss (カール・フリードリヒ・ガウス) は 1850 年に友人 Heinrich Schumacher (ハインリッヒ・シューマッハ) へ書いた手紙の中で、Franz Nauck (フランツ・ナウク) によって発見された 8 クイーン問題が 92 個の答えを持つという事実は、数時間試行錯誤を繰り返せば簡単に確認できると記しています (Schwer ist es übrigens nicht, durch ein methodisches Tatonnieren sich diese Gewissheit zu verschaffen, wenn man eine oder ein paar Stunden daran wenden will.)。彼の用いた Tatonniren という言葉は、周りが見えない暗闇の中で周りの様子を手探りで確かめるという意味のフランス語 tâtonner から来ています。

Gauss がこの手紙で説明した解法を紹介します。同じ解法はフランス人娯楽数学者 Édouard Lucas (エドゥアール・リュカ) も 1882 年に発表しており、Lucas はこの解法を Emmanuel Laquière (エマニュエル・ラキエ) から得たとしています。\(n\) クイーン問題の条件を満たすクイーンの配置を配列 \(Q[1..n]\) で表すことにします。ここで \(Q[i]\) は \(i\) 列におけるクイーンの場所を表します。こうすれば、クイーンを一番上の列から列ごとにひとつずつ盤に置いていくという再帰的な戦略で解を求めることができます。具体的には、\(r\) 番目のクイーンを置くときに盤の \(r\) 列目にある \(n\) 個のマスを単純な for ループで調べ、もしあるマスがそれまでに置いたクイーンによって攻撃されるなら、そのマスは無視します。そうでなければ、そのマスにクイーンを暫定的に配置し、他のクイーンを以降の列に配置できるかどうかを再帰的に調べます。

アルゴリズム全体を次に示します。このアルゴリズムは途中まで完了したクイーンの配置を受け取り、その配置と矛盾しない \(n\) クイーン問題の解を全て枚挙します。 入力 \(r\) は次にクイーンを置く列の添え字であり、\(Q[1..r-1]\) は最初の \(r - 1\) 個のクイーンの配置です。\(\textsc{PlaceQueens}(Q[1..n], 1)\) を呼べば追加の制約がない \(n\) クイーン問題の解を全ての枚挙できます。外側の for ループが \(r\) 列におけるクイーンの配置を走査し、内側の for ループが \(r\) 列へのその配置がこれまでに配置された \(r - 1\) 個のクイーンから攻撃されるかどうかを調べます。

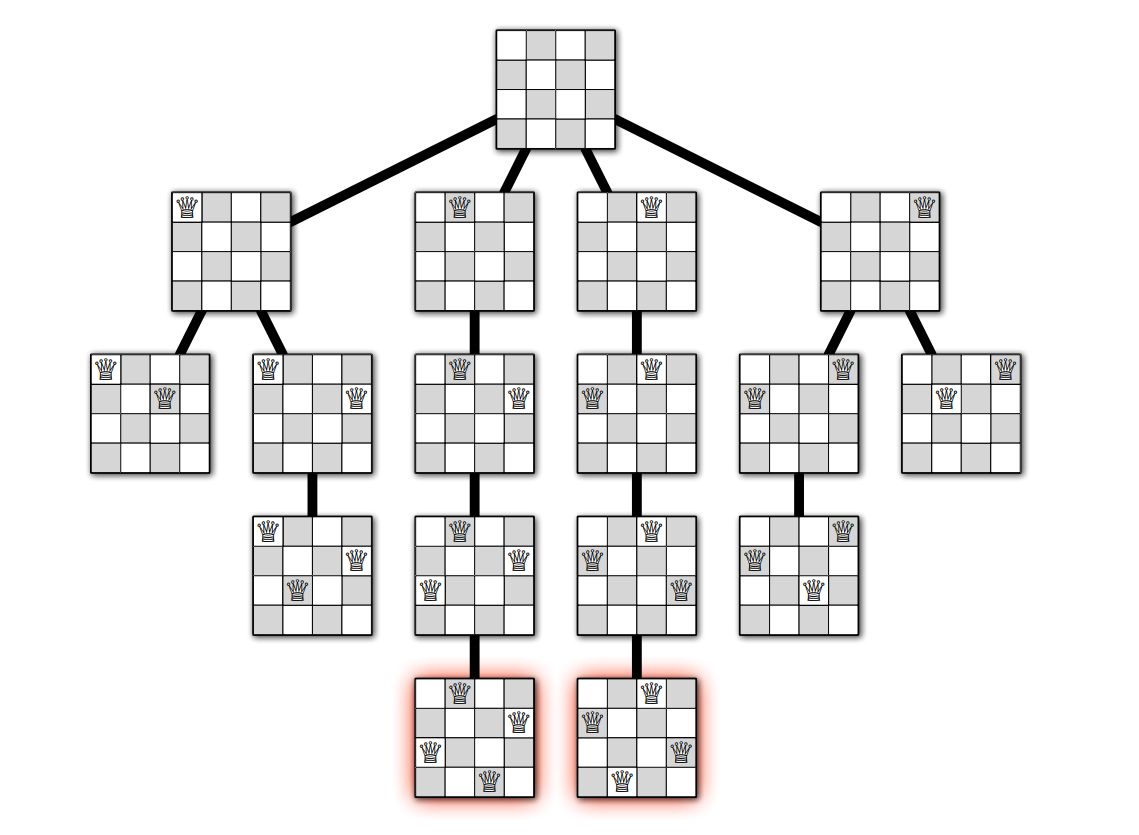
\(\textsc{PlaceQueens}\) の実行は再帰木 (recursion tree) を使って可視化できます。再帰木の頂点は再帰的に呼ばれる小問題に対応し、このアルゴリズムでは制約を満たす部分解を表します。再帰木の根は何も配置されていない盤 (\(r = 0\)) を、辺は再帰呼び出しを、葉はクイーンをそれ以上配置できない部分解を表します。クイーンが配置できない理由は全ての列にクイーンが配置されているためか、そうでなければ空の列の全てのマスがそれまでに配置されたクイーンから攻撃されるためです。バックトラッキングを使った完全な解の探索はこの木に対する深さ優先探索と同じ動きをします。

ゲーム木

正方形のマス目からなる \(n \times n\) の格子を使った次の単純な二人対戦ゲームを考えます¹。このゲームは二人のプレイヤー Horace Fahlberg-Remsen (ホレース・ファールベルグ・レムセン) と Vera Rebaudi (ベラ・レバウディ)²が \(n\) 個の駒を盤の反対側に向かって移動させるゲームです。Horace の駒は左端の列に一列に並んだ状態でスタートし、水平方向に (horizontally) 右へ移動します。同じように Vera の駒は一番上の行に一列に並んだ状態からスタートし、一番下の列を目指して垂直に (vertically) 移動します。Horace は各ターンで二つの操作のうち一つを行うことができます。つまり、ある駒を一つ右の空のマスに移動させる move か、ある駒を Vera の駒をちょうど一つ飛び越して二つ隣の空のマスに移動させる jump です。全ての駒が move も jump もできない場合 Horace はパスとなります。同様に Vera は駒を一つ選んで下方向に move か jump を行うことができ、そのような操作ができなければパスです。最初に全ての駒を反対側まで移動させたプレイヤーの勝ちです (駒が盤の上にある限りプレイヤーのどちらかは合法的な手を打ち続けることができ、最終的に必ずどちらかのプレイヤーが勝つことを示すのは難しくありません) 。

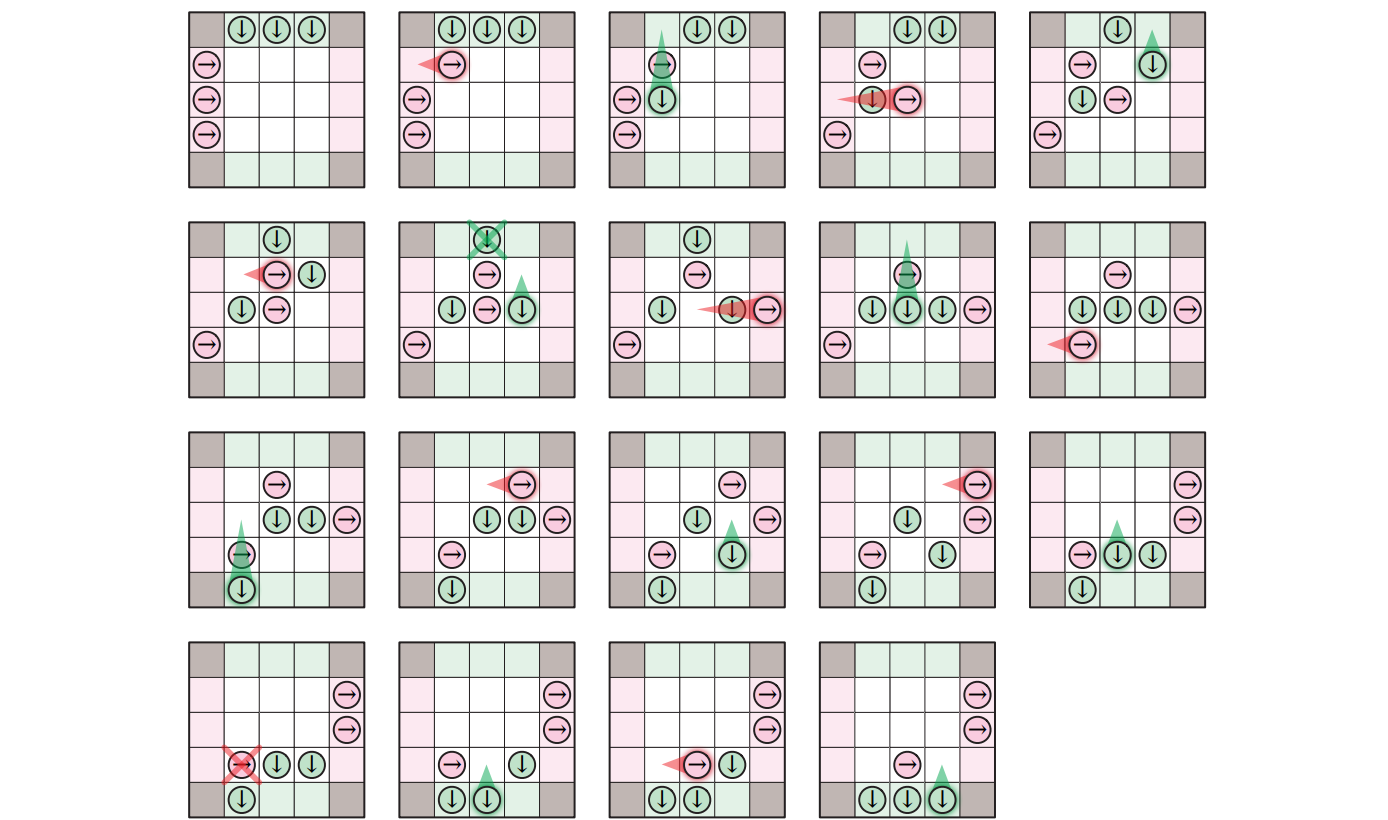
このゲームを過去に見たことがない限り³、どうすればこのゲームをうまくプレイできるか分からないでしょう。しかしこうして紹介しているのですから、もちろん、このゲームには完璧なプレイをする比較的単純なバックトラッキングを使ったアルゴリズムが存在します。つまり、完璧なプレイヤーとのゲームに途中から参加参加したときに、どうやって勝つかを (勝つことが可能ならば) 教えてくれるアルゴリズムがあるということです ――同様の戦術はランダム性がなく隠された情報がない任意の二人対戦ゲームに対して存在します。

ゲームの状態 (state) とは駒の位置と現在プレイヤーがどちらであるかという情報です。状態 \(x\) から状態 \(y\) に遷移できる場合に限って二つの状態を結ぶようにすると、ゲーム木 (game tree) ができます。この木の根はゲームの初期状態であり、根から葉への道は起こりうるゲームの展開の一つを表します。

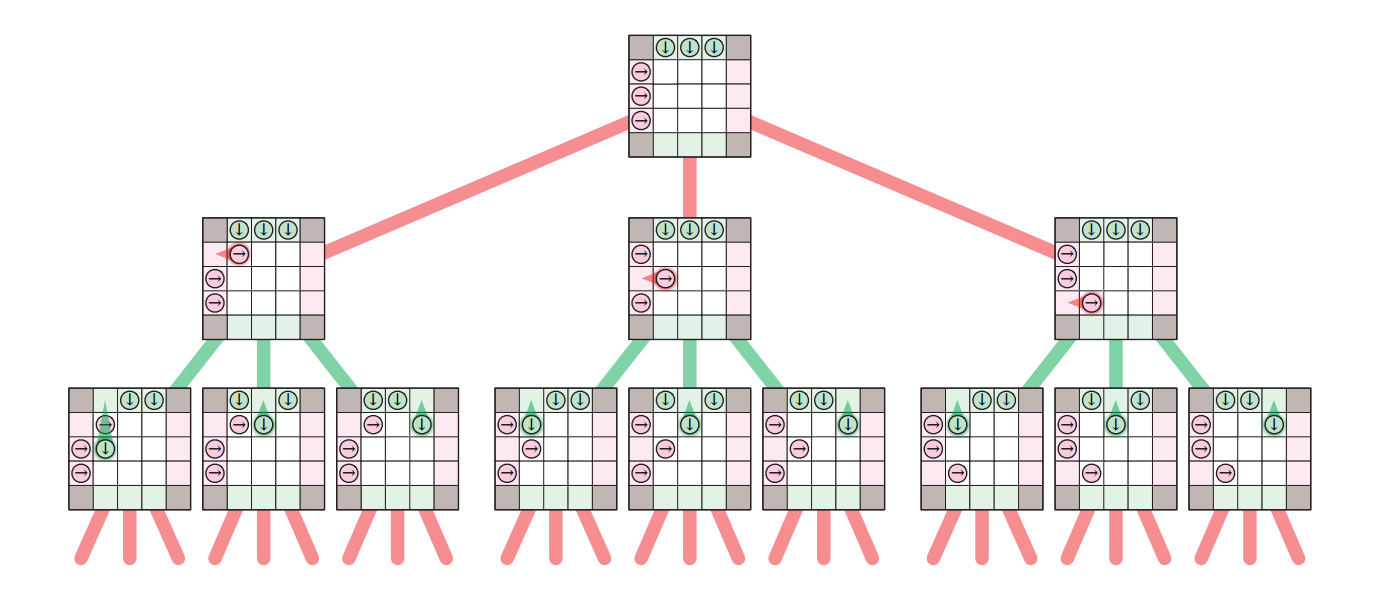
このゲーム木を理解しやすくするために、良い (good) 状態と悪い (bad) 状態を次のように定義します:

• 良いゲーム状態とは、現在のプレイヤーが勝っているか、相手が悪い状態になるような手を現在のプレイヤーが打てる状態。
• 悪いゲーム状態とは、現在のプレイヤーが負けているか、どんな手を打っても相手が良い状態になる状態。

言い換えると、ゲーム木の葉でない頂点が良いとはその子の少なくとも一つが悪いことであり、葉でない頂点が悪いとはその子の全てが良いことです。帰納法によって、良い状態にあるプレイヤーは相手が完璧にプレイしたとしてもゲームに勝利できることが示せます。反対に、悪い状態にあるプレイヤーは相手がミスをしない限り勝利できません。この再帰的な定義は 1913 年に Ernst Zermelo (エルンスト・ツェルメロ) によって初めて提案されました⁴。

この再帰的な定義を使うと、与えられた状態が良いか悪いかを判定する次のバックトラッキングを使ったアルゴリズムをすぐに得ます。本質的には、このアルゴリズムが行うのはゲーム木の深さ優先探索であり、このアルゴリズムの再帰木はゲーム木そのものです。このアルゴリズムを少し変更すれば良い手 (あるいは全ての良い手) を入力の状態に対して出力するようにできます。

ゲームをプレイするどんなアルゴリズムも、突き詰めればこのバックトラッキングを使った戦略に基づいています。しかしたいていのゲームでは状態の数が膨大になるので、ゲーム木全体を走査するのは現実的ではありません。そのためゲームのプログラムではヒューリスティック⁵を使ってゲーム木の刈り取りを行います。例えば、明らかに (あるいは"明らかに") 良い/悪い状態や、他の状態よりも良い/悪い状態を無視したり、葉を評価するもっと効率的なヒューリスティックを使って木の走査を途中で打ち切ったりします。

部分和

\(\textsc{SubsetSum}\) というもっと複雑な問題を考えましょう。正の整数の集合 \(X\) とターゲットとなる整数 \(T\) が与えられたときに、和が \(T\) となる \(X\) の部分集合を求める問題です。

条件を満たす部分集合が複数存在しても構わないことに注意してください。例えば \(X = \lbrace 8,6,7\) \(,5,3,10,\) \(9 \rbrace\) で \(T = 15\) のとき、答えは \(\textsc{True}\) であり、和が 15 になる部分集合は \(\lbrace 8, 7 \rbrace\), \(\lbrace 7,5,3 \rbrace\), \(\lbrace 6, 9 \rbrace\) の三つです。一方 \(X = \lbrace 11, 6, 5, 1, 7, 13, 12 \rbrace\) で \(T = 15\) のとき、答えは \(\textsc{False}\) です。

自明なケースが二つあります。一つは \(T = 0\) のときで、この場合すぐに \(\textsc{True}\) を答えることができます。なぜなら空集合は任意の集合 \(X\) の部分集合であり、要素の和が \(0\) だからです⁶。もう一つは "\(T < 0\)" または "\(T \neq 0\) かつ \(X\) が空集合" のときで、この場合は答えが \(\textsc{False}\) であるとすぐに分かります。

一般の場合について、\(x \in X\) を任意に取ってきたとします (\(X\) が空の場合は既に処理しました)。 和が \(T\) となる \(X\) の部分集合が存在するのは、次の条件どちらかが真のときです:

• \(x\) を含む \(X\) の部分集合であって和が \(T\) になるものが存在する。
• \(x\) を含まない \(X\) の部分集合であって和が \(T\) になるものが存在する。

最初の場合では、\(X \backslash \lbrace x \rbrace\) の部分集合であって和が \(T - x\) であるものが存在します。二つ目の場合では、\(X \backslash \lbrace x \rbrace\) の部分集合であって和が \(T\) であるものが存在します。したがって、\(\textsc{SubsetSum}(X, T)\) という問題を \(\textsc{SubsetSum}(X \backslash \lbrace x \rbrace, T - x)\) と \(\textsc{SubsetSum}(X \backslash \lbrace x \rbrace, T)\) というより単純なインスタンスに帰着させることができます。この考え方によるアルゴリズムを以下に示します:

正しさ

このアルゴリズムの正しさの証明は帰納法の簡単な練習問題としてちょうどいいでしょう:

\(T = 0\) のとき、空集合の和が \(T\) と等しくなるので、\(\textsc{True}\) が正しい答えです。 \(T\) が負または \(X\) が空のとき、和が \(T\) となる \(X\) の部分集合は存在しないので、\(\textsc{False}\) が正しい答えです。そうでなければ、和が \(T\) となる \(X\) の部分集合は \(x\) を含むか含まないかのどちらかであり、どちらの場合も再帰の妖精によって正しくチェックされます。証明終わり。

解析

このアルゴリズムを解析するには、実装の詳細を正確に決める必要があります。まず入力の集合 \(X\) は配列 \(X[1..n]\) と表されているとします。

アルゴリズムの再帰の部分で、任意の要素 \(x \in X\) を選ぶ操作があります。残りの要素 \(X \backslash \lbrace x \rbrace\) がなるべく簡単に表記できてかつ簡単に計算できるような \(x\) を選んで再帰呼び出しのオーバーヘッドを抑えることが望ましいので、ここでは配列の最後の要素 \(X[n]\) を \(x\) として選ぶことにします。こうすれば部分集合 \(X \backslash \lbrace x \rbrace\) は \(X[1..n-1]\) と表記できます。

また再帰呼び出しにおいて部分配列の完全なコピーを渡すのは ――配列のコピーは \(\Theta(n)\) 時間の処理なために―― 時間がかかりすぎるので、代わりに配列への参照 (あるいは開始アドレス) とその長さだけを再帰呼び出しに渡すようにします (\(X\) をグローバル変数にして、再帰呼び出しで \(X\) への参照を渡さないようにもできます)。

実装をこのように選べば、このアルゴリズムの実行時間 \(T(n)\) は再帰方程式 \(T(n) \leq T(n - 1) + O(1)\) を満たし、その解は \(T(n) = O(2^{n})\) です。求めるには再帰木を使うか、「あ、この再帰方程式って Hanoi の塔で解いたじゃん」を使います。最悪ケース ――例えば \(T\) が \(X\) の全ての要素の和よりも大きい場合―― では再帰木が高さ \(n\) の完全二分木となり、このアルゴリズムは \(2^{n}\) 個ある \(X\) の部分集合を全て調べます。

変種

ここまで説明してきたアルゴリズムを少しだけ変更すれば、\(\textsc{SubsetSum}\) 問題の変種を解くことができます。例えば次に示すのは、和が \(T\) となる \(X\) の部分集合が存在するなら実際に構築してそれを返し、存在しないならエラー値 \(\textsc{None}\) を返すアルゴリズムです。このアルゴリズムで使われている再帰的な戦略はこれまでの判定問題に対するものと全く同じであり、実行時間は \(O(2^{n})\) です。実行時間の解析は新しい要素の追加が \(O(1)\) 時間で行えるデータ構造 (例えば単純連結リスト) を仮定すると簡単に行えますが、仮に新しい要素の追加に \(O(n)\) 時間がかかるデータ構造 (例えばソート済み配列) を使ったとしても実行時間は \(O(2^{n})\) で変わりません。

\(\textsc{SubsetSum}\) 問題の他の変種としては、和がある値になる部分集合の数を数える問題や和がある値になる部分集合の中で何らかの基準に沿って一番良いものを選ぶ問題などがあります。

バックトラッキングを使って解けるたいていの問題には、この「同じ再帰的な戦略がその問題のたくさんの変種に対して使える」という特徴があります。例えば一つ前の節で紹介したあるゲームの状態が良いか悪いかを求める問題では、見つかった良い手を返したり、全ての良い手を含む配列を返すようにアルゴリズムを改変するのは簡単です。

このことから、バックトラッキングを使ったアルゴリズムを設計するときには、問題の変種の中で可能な限り一番単純なものを考えるべきだということが言えます。複雑な情報やデータ構造ではなくて、一つの値や真偽値を求める問題が最初に考えるものとして適しているでしょう。

共通するパターン

バックトラッキングを使ったアルゴリズムはどれも、特定の制約を満たす再帰的に定義された構造の構築を目標として決断の列 (decision sequence) を作っていきます。目標となる構造そのものが求める決断の列であることもありますが、常にそうだというわけではありません。これまでの例でいうと:

• \(n\) クイーン問題では、目標は各列におけるクイーンの配置の列であり、どの二つのクイーンもお互いを攻撃できてはいけないという制約がありました。アルゴリズムは各列について、クイーンをどこに置くかを決断します。

• ゲーム木の問題では、目標は合法な手の列であり、選択する手はプレイヤーにとって良いものでなければならないという制約がありました。アルゴリズムは各ゲームの状態について、良い手がどれであるかを決断します。

• 部分和の問題では、目標は入力要素の部分列であり、和が特定の値にならなくてはならないという制約がありました。アルゴリズムは各入力要素について、その要素を出力の配列に入れるかどうかを決断します。

(部分和の問題 "\(\textsc{SubsetSum}\)" の目標が部分集合 (subset) ではなく列 (sequence) を求めることなのはどうしてでしょうか？ これは意図的にこうしたのでした。入力の集合が (実装の詳細が不明なデータ構造ではなくて) 配列で与えられると再帰的アルゴリズムの説明と解析が簡単になるのでそうしたというだけのことです)

バックトラッキングを使ったアルゴリズムの再帰呼び出しでは、過去の決断と矛盾しないちょうど一つの決断をする必要があります。そのため再帰呼び出しの引数には未処理の入力データだけではなくて、これまでの決断の結果をわかりやすくまとめたデータも含まれます。これまでの例でいうと:

• \(n\) クイーン問題では、空の列の数だけではなくてこれまでに配置されたクイーンの位置もアルゴリズムに渡す必要がありました。この問題では、面白くないのですが、これまでの決断を完全な形で覚えなければなりません。

• ゲーム木の問題では、現在のゲームの状態と次に手を打つプレイヤーをアルゴリズムに渡すだけで済みました。あるゲームの状態からどちらのプレイヤーが勝つかはそれまでのプレイヤーの打った手に依存していないために、それまでの決断を覚えておく必要は全くありません⁷。

• 部分和の問題では、アルゴリズムの入力は残っている整数と残りの和の値二つでした。この残りの和の値は元々の問題で目標となっていた和の値からこれまでに選ばれた要素の和を引いたものです。実際にどの要素が選ばれたかは重要ではありませんでした。

バックトラッキングを使ったアルゴリズムを設計するときには、アルゴリズムの途中で必要となるそれまでの決断についての情報が何かを最初に明らかにしておく必要があります。この情報が自明でない場合には、アルゴリズムが解こうとしているよりも一般的な問題を解かなければなりません。この種類の一般化はこれまでに出てきています: ソートされていない配列の中央値を線形時間で見つけるときには、任意の \(k\) に対して \(k\) 番目に小さい要素を見つけるアルゴリズムを考える必要がありました。

解くべき再帰的な問題を特定したら、最後にはその問題を再帰的な総当たりで解きます。つまり、次の決断についての選択肢のうちこれまでの決断と矛盾しないものを全て試し、残りは再帰の妖精に任せます。この部分に賢さはありません。 "明らかに" 馬鹿げた選択肢を飛ばすということはせず、全て試します。このアルゴリズムの高速化は後で触れます。

分かち書き (Interpunctio Verborum)

空白も句読点もない外国語の文章を単語ごとに区切りたいとします。例えば次の文章は、Lucius Licinius Murena (ルシウス・リキニウス・ムレナ) を弁護するために Cicero (キケロ) が紀元前 62 年に行った有名な演説を、古典ラテン語の標準的な記法 scriptio continua で表したものです⁸:

PRIMVSDIGNITASINTAMTENVISCIENTIANONPOTESTESSERESENIMSVNTPARVAEPROPEINSINGVLISLITTERISATQVEINTERPVNCTIONIBUSVERBORVMOCCVPATAE

ラテン語が流暢な読者は、この文字列を (現代的な正書法で) Primus dignitas in tam tenui scientia non potest esse; res enim sunt parvae, prope in singulis litteris atque interpunctionibus verborum occupatae とパースできるでしょう⁹。

このような文字列の分割のことを "分かち書き" と言います。分かち書きの問題は古典ラテン語と古典ギリシャ語だけが持つ問題ではなく、バリ語、ビルマ語、中国語、日本語、ジャバ語、クメール語、ラオス語、タイ語、チベット語、ベトナム語などの現代の言語でも同様の問題が発生します。似たような問題は他にも、句読点のない英語の文章の文への分割¹⁰、段落ごとに分割された文章を組版するときの行への分割、音声認識、手書き文字認識、曲線の単純化、そして一部の時系列解析などで生じます。ここでは可視化のしやすさを考えて、現代英語のアルファベットからなる文字列を英単語ごとに分割する問題を考えます。

まず明らかなのは、複数の方法で分割できる文字列もあるということです。例えば \(\color{maroon} \texttt{BOTH} \)\( \color{maroon} \texttt{EART} \)\( \color{maroon} \texttt{HAND} \)\( \color{maroon} \texttt{SATU} \)\( \color{maroon} \texttt{RNSPIN}\) は \(\color{maroon} \texttt{BOTH} \cdot {} \)\( \color{maroon} \texttt{EARTH} \cdot {} \)\( \color{maroon} \texttt{AND} \cdot {} \)\( \color{maroon} \texttt{SATURN} \cdot {} \)\( \color{maroon} \texttt{SPIN}\) にも \(\color{maroon} \texttt{BOT} \cdot {} \)\( \color{maroon} \texttt{HEART} \cdot {} \)\( \color{maroon} \texttt{HANDS} \cdot {} \)\( \color{maroon} \texttt{AT} \cdot \texttt{URNS} \cdot {} \)\( \color{maroon} \texttt{PIN}\) にも分割できますし、他にも分割方法があります。しかしまずは、一番単純な問題「入力の文字列を英単語ごとに分割する方法は一つでも存在するか？」を考えることにします。

問題を具体的に (そして違う言語でも使えるように) するために、サブルーチン \(\textsc{IsWord}(w)\) が使えると仮定します。このサブルーチンは文字列 \(w\) を受け取り、その文字列が "単語" ならば \(\textsc{True}\) を、そうでなければ \(\textsc{False}\) を返します。例えば右から読んでも左から読んでも同じになる単語ごとに文字列を分割しようとしているのなら、右から読んでも左から読んでも同じになる単語が "単語" になり、\(\textsc{IsWord} ({\color{maroon}{ \texttt{ROTATOR}}}) ={}\)\(\textsc{True}\) および \(\textsc{IsWord} ({\color{maroon}{ \texttt{PALINDROME}}}) ={}\)\(\textsc{False}\) です。

部分和問題と同じように、分かち書き問題への入力も列 (sequence) という構造を持ちます。ただこの問題の入力は数字の列ではなくて文字の列なので、アルゴリズムが入力を左から右に読むとした方が自然です。同様に、出力の構造は単語の列であり、アルゴリズムは左から右に単語を出力するとしましょう。分割アルゴリズムの途中に放り込まれたところを想像すると、次の画像のような状態になります。

これまでの決断の列 ――最初の 17 文字の 4 つの単語への分割―― とこれから処理する文字列が、黒いバーによって分かれています。

この想像上の処理で次に行われるのは、次に出力する単語の終端の決断です。今考えている例では、次に出力する単語の選択肢が四つ (\(\color{maroon}{\texttt{HE}}\), \(\color{maroon}{\texttt{HEAR}}\), \(\color{maroon}{\texttt{HEART}}\), \(\color{maroon}{\texttt{HEARTH}}\)) あります。これらのうちどれを選べば入力文字列全体の分割が上手く行くのか、あるいはどれを選んでも上手く行かないのかは全く分かりません。もちろん "賢く" なってどの選択肢が良いのかを調べることもできますが、それをするにはいろいろと考えなくてはいけません！ そうする代わりに、ここでは "愚直に" 全ての選択肢を総当たりで試すことにします。こうすると、残りの処理は再帰の妖精に任せることができます:

• まず次の単語として \(\color{maroon}{\texttt{HE}}\) を暫定的に受け入れ、後は再帰の妖精に任せる。

  

• それから次の単語として \(\color{maroon}{\texttt{HEAR}}\) を暫定的に受け入れ、後は決断は再帰の妖精に任せる。

  

• それから次の単語として \(\color{maroon}{\texttt{HEART}}\) を暫定的に受け入れ、後は決断は再帰の妖精に任せる。

  

• それから次の単語として \(\color{maroon}{\texttt{HEARTH}}\) を暫定的に受け入れ、後は決断は再帰の妖精に任せる。

  

再帰の妖精が少なくとも一回成功を報告したら、この処理も成功を報告します。そうでなくて全ての再帰の妖精が失敗を報告したとき ――どうやっても次の語が作れない場合も含む―― には、失敗を報告します。

未処理の文字列の接頭語だけが次の決断の選択肢を決めるので、これまでの決断が現在の選択肢に影響することはありません。例えば異なる決断の結果としてこれから処理する文字列が同じになることがありますが、この場合の選択肢は同じになります。

こうするとバックトラッキングを使ったアルゴリズムの単純な基本構造がはっきりします:

再帰的なアルゴリズムを完全なものにするには、ベースケースの処理が必要です。この再帰的な戦略が終了するのは処理が入力文字列の終端に達してこれ以上単語を作れなくなったときです。もちろん、空文字列はゼロ個の単語へとユニークに分割できます！

以上をまとめると、次のシンプルな再帰的アルゴリズムが手に入ります:

添え字による定式化

実際のプログラムでアルゴリズムの入力パラメータに配列をコピーして渡すと時間がかかってしまうので、再帰的な小問題を組み立てるためのもっとコンパクトな方法を考えた方が良さそうです。このような状況でアルゴリズムを設計するときには、最初の問題に対する入力をグローバル変数として扱い、実際の小配列ではなくて元の配列に対する添え字を使うように問題とアルゴリズムを変形してしまうのがとても有用です。

今考えている分かち書き問題では、再帰呼び出しの引数は常に最初の問題に対する入力配列の接尾部分 \(A[i..n]\) です。よって \(A[1..n]\) をグローバル変数とみなせば、再帰的な問題を次のように変形できます:

このアルゴリズムを説明するために二つの真偽値関数を導入します:

• 任意の添え字 \(i, j\) に対して \(\mathit{IsWord}(i, j) = \textsc{True}\) は \(A[i..j]\) が単語であることと同値である (このような関数は与えられると仮定している)。

• 任意の添え字 \(i\) に対して \(\mathit{Splittable} (i) = \textsc{True}\) は配列 \(A[i..n]\) が単語に分割できることと同値である (この関数をこれから実装する)。

例えば \(\mathit{IsWord}(1, n) = \textsc{True}\) となるのは入力全体が一つの単語であるときであり、\(\mathit{Splittable}(1) = \textsc{True}\) となるのは入力文字列全体が分割できるときです。これまで説明してきた再帰的な戦略から、次の再帰方程式を得ます: \[ \mathit{Splittable}(i) = \begin{cases} \textsc{True} & \text{if } i > n \\ \bigvee\limits_{j = i}^{n}(\mathit{IsWord} (i, j) \land \mathit{Splittable}(j + 1)) & \text{それ以外} \end{cases} \] これはついさっき見たアルゴリズムと表記が変わっただけで全く同じです。再帰方程式を疑似コードにすると似ていることがさらに分かりやすくなります:

表記の違いは自明で何も変わらないと思うかもしれません。しかし表記を変えることでプログラムを実装したときの実行時間が小さくなるだけではなく、線形計画法のアルゴリズムの設計も容易になります。線形計画法については次の章で扱います。

❤ 解析

バックトラッキングを使ったアルゴリズムの多くは最悪ケースにおける実行時間が指数時間となりますが、特に驚くようなことではないでしょう。こういったアルゴリズムの実行時間の正確な解析はこの本の範囲を超えます。しかし幸いにも、この本に出てくるバックトラッキングを使ったアルゴリズムはもっと効率的なアルゴリズムのための中間的な結果に過ぎないので、最悪ケースにおける正確な実行時間はあまり重要ではありません ("まず動くようにせよ。それから速くせよ")。

ただ面白そうなので、再帰的なアルゴリズム \(\textsc{Splittable}\) の実行時間の解析をしてみることにします。\(\textsc{IsWord}\) がどんな動作をしてどれくらい時間がかかるのかわからないので¹¹、実行時間の解析は \(\textsc{IsWord}\) の呼び出し回数を通して行います。

\(\textsc{Splittable}\) は入力文字列の全ての接頭辞に対して \(\textsc{IsWord}\) を呼びます。また出力文字列の接尾語全てに対して再帰呼び出しをする可能性があります。よって \(\textsc{Splittable}\) の "実行時間" は次のぎょっとする形の再帰方程式に従います: \[ T(n) \leq \sum_{i=0}^{n-1}T(i) + O(n) \] しかし次に説明するトリックを理解してしまえば、この式は見た目ほど恐ろしいものではありません。

まず \(O(n)\) を適当な定数 \(\alpha\) を使って \(\alpha n\) と明示的に書き直します (\(\alpha\) の実際の値は重要ではありません)。さらに最悪ケースの実行時間を解析していることから、全ての再帰呼び出しが行われると仮定します¹²。そうした上で \(T(n)\) から \(T(n-1)\) を引くと、"全ての \(n\) に対する" 再帰方程式を、"直前の \(n\) に対する" 再帰的方程式に変形できます: \[ \begin{aligned} T(n) & = \sum_{i=0}^{n-1}T(i) + \alpha n \\ T(n-1) & = \sum_{i=0}^{n-2}T(i) + \alpha (n - 1) \\ \therefore T(n) - T(n - 1) & = T(n - 1) + \alpha \end{aligned} \] 最後の式は \(T(n) = 2\ T(n - 1) + \alpha\) と変形できます。ここまでくれば、\(T(n) = O(2^{n})\) と自信をもって予想できます (あるいは再帰木を使って実際に計算してもいいですし、Hanoi の塔の例を思い出してもいいでしょう)。元々の全ての \(n\) に対する再帰方程式がこの上界を持つことを帰納法で証明するのは難しくありません。

さらに言えば、この解析は最良です。長さ \(n\) の文字列を分割する方法は ――最後の文字を除くそれぞれの文字で単語が終わるかどうかという選択肢があるので―― ちょうど \(2^{n-1}\) 通りあり、最悪ケースにおいて \(\textsc{Splittable}\) は \(2^{n-1}\) 個の選択肢全てを探索するからです。

変種

部分和問題と同様に、一番単純な分かち書き問題の再帰的な構造を理解すれば、様々な変種を同じ構造を使って解くことができます。ここではその一つを説明して、練習問題でさらにいくつかを考えます。いつも通り、最初の問題に対する入力は \(A[1..n]\) であるとします。

文字列が複数の単語列に分割できるときに、何らかの基準に従って最も良い分割を選択したい場合があります。また逆に文字列が単語列に分割できないときにも、失敗を報告するのではなくて一番良い分割を選択したい場合があります。これら両方を達成するために、文字列を受け取ってそのスコアを数値として返す二つ目の外部関数 \(\mathit{Score}\) が利用できると仮定します。例えばめったに表れない長い単語には高い正の点数、頻繁に登場する短い単語には低い正の点数、スペルミスには多少の負の点数、長くて単語にもなっていない文字列にはかなり低い負の点数が付けられるでしょう。ここでの目標は入力文字列の単語列への分割であってスコアの和が最大のものを求めることです。

任意の添え字 \(i\) に対して、入力文字列の接尾部分 \(A[i..n]\) の分割のうちスコアが最大のものを \(\mathit{MaxScore}(i)\) で表すことにします。この関数は次の再帰方程式を満たします: \[ \mathit{MaxScore}(i) = \begin{cases} 0 & \text{if } i > n \\ \max\limits_{i \leq j \leq n} \left( \mathit{Score}(A[i..j]) + \mathit{MaxScore}(j + 1) \right) & \text{それ以外} \end{cases} \] この関数は \(\mathit{Splittable}\) に対して得たものと本質的に同一です。唯一の違いは真偽値演算 \(\vee, \wedge\) が数値演算 \(\max, +\) に代わっている点です。

最長増加部分列

任意の列 \(S\) に対して、\(S\) からゼロ個以上の要素を削除してできる列を部分列 (subsequence) と言います。このとき残った要素の順番は変更せず、部分列の要素は \(S\) で隣り合っている必要はありません。

例えば街の大通りを車で通って信号の列 \(S\) を通り過ぎるとき、あなたが車を停めるのは赤になっている信号からなる \(S\) の部分列です。運が良ければ信号で全く停まらずに済みますが、その場合に対応する空列も \(S\) の部分列です。また運が悪くて全ての信号につかまった場合に対応する \(S\) 自身も \(S\) の部分列となります。

もう一つ例をあげると、\(\color{maroon}{\texttt{BENT}}\), \(\color{maroon}{\texttt{ACKACK}}\), \(\color{maroon}{\texttt{SQUARING}}\), \(\color{maroon}{\texttt{SUBSEQUENT}}\) は全て \(\color{maroon} \texttt{SUBS} \)\( \color{maroon} \texttt{EQUE} \)\( \color{maroon} \texttt{NCEB} \)\( \color{maroon} \texttt{ACKT} \)\( \color{maroon} \texttt{RACK} \)\( \color{maroon} \texttt{ING}\) の部分列であり、空文字列と \(\color{maroon}\texttt{SUBS} \)\( \color{maroon} \texttt{EQUE} \)\( \color{maroon} \texttt{NCEB} \)\( \color{maroon} \texttt{ACKT} \)\( \color{maroon} \texttt{RACK} \)\( \color{maroon} \texttt{ING}\) 自身もそうです。また \(\color{maroon} \texttt{QUEUE}\), \(\color{maroon} \texttt{EQUUS}\), \(\color{maroon} \texttt{TALLYHO}\) はどれも部分列ではありません。部分列であってその要素が元の列において連続しているものを、部分文字列 (substring) と言います。例えば \(\color{maroon}{\texttt{MASHER, LAUGHTER}}\) はどちらも \(\color{maroon}{\texttt{MANSLAUGHTER}}\) の部分列ですが、部分文字列なのは \(\color{maroon}{\texttt{LAUGHTER}}\) だけです。

整数列が与えられたときに、要素が昇順に並んでいる部分列で一番長いものを見つける問題を考えます。きちんと言うと、\(A[1..n]\) が与えられたときに、 全ての \(k\) に対して \(A[i_{k}] < A[i_{k+1}]\) が成り立つ添え字の列 \(1 \leq i_{1} < i_{2} < \cdots < i_{l} \leq n\) で一番長いものを求める問題です。

この最長増加部分列 (longest increasing subsequence) 問題に対する自然なアプローチは、\(1\) から \(n\) までの添え字 \(j\) について、\(A[j]\) が最長増加部分列に入るかどうかを決断していくというものです。処理の途中に放り込まれたところを想像すると、次の図のようになります:

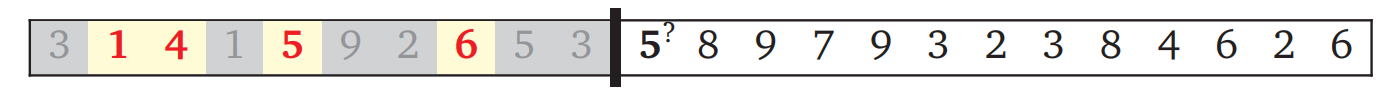
分かち書き問題の例と同じように、これまでの決断と未処理の入力が黒いバーで分かれています。出力の部分列に入れるように決断した数がハイライトされ、除外された数はグレーになっています (部分列に入れた数が昇順なことに注意してください！)。アルゴリズムが決断するのはバーのすぐ後ろの数を部分列に入れるかどうかです。

この例では次の数字 \(5\) が最後に選択した数字 \(6\) よりも小さいので、次の数字を部分列に入れることはできません。そのためそのまま次の決断に進みます:

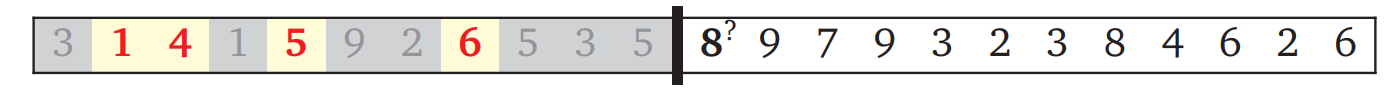
この状況では \(8\) を部分列に入れられますが、そうすべきかは分かりません。ここでもバックトラッキングを使ったアルゴリズムは "賢く" ならず、総当たりを使います:

• まず暫定的に \(8\) を部分列に入れる。そして再帰の妖精に残りの決断を任せる。
• 次に暫定的に \(8\) を部分列から外す。そして再帰の妖精に残りの決断を任せる。

長い部分列を返した方を選択します。これは部分和問題を解くときに使った再帰的なパターンと全く同じです。

続いて鍵となるこの問題を考えます: 「これまでの決断について覚えるべき情報は何か？」 \(A[j]\) を部分列に入れられるのは出来上がる部分列が昇順に並ぶときだけです。これまでの決断の結果から定義される \(A[1..j-1]\) の部分列は (帰納法により！) 昇順なので、\(A[j]\) を入れられるのは選択した \(A[1..j-1]\) の部分列の最後の要素よりも \(A[j]\) が大きいときだけです。したがって、過去について記憶しておくべき情報は最後に選択した数となります。この事実を使うと、前述の図から必要のない情報を取り除けます:

よって再帰的な戦略が実際に解くべきなのは次の問題です:

いつも通り、この再帰的な戦略にはベースケースが必要です。この戦略は配列の終端まで進むと "次の要素" が存在しなくなってそれ以上進めなくなるからです。空配列の部分列は空配列だけであり、「配列の要素が全て昇順に並んでいる」という命題が空配列に対して真であるために、空配列は増加列です。したがってベースケースである空配列の最長増加部分列の長さは \(0\) です。

以上の説明から、次のアルゴリズムが得られます:

ここで思い出してほしいのですが、配列を直接コールスタックに積むのは時間がかかる処理なのでした。そこで高速化のために、 \(A[1..n]\) をグローバル変数として配列の添え字を使って同じ処理をする方法を考えます。整数 \(\mathit{prev}\) は配列の要素 \(A[i]\) と表すことができ、再帰呼び出しに渡される配列の接尾部分は \(A[j..n]\) と表すことができます。したがって前述の再帰的な問題を添え字を使って次のように変形できます:

全ての要素が \(A[i]\) よりも大きい \(A[j..n]\) の部分列の中で一番長いものの長さを \(\mathit{LISBigger}(i, j)\) とすると、前述の再帰的な戦略から次の再帰方程式が得られます: \[ \mathit{LISBigger}(i, j) = \begin{cases} 0 & \text{if } j > n \\ \mathit{LISBigger}(i, j + 1) & \text{if } A[i] \geq A[j] \\ \max \left\lbrace \begin{array}{c} \mathit{LISBigger} (i, j + 1) \\ 1 + \mathit{LISBigger}(j, j + 1) \end{array} \right\rbrace & \text{それ以外} \end{cases} \] もし疑似コードがお好みなら:

最後に、このアルゴリズムを使って制約の無い元の問題を解きます。配列の最初に門番 (sentinel) として \(-\infty\) を追加するのが一番簡単です:

\(\textsc{LisBigger}\) の実行時間は Hanoi の塔と同じ再帰方程式 \(T(n) \leq 2\ T(n-1) + O(1)\) を満たし、\(T(n) = O(2^{n})\) です。この結果は驚くべきことではありません。というのも、最悪ケースにおいてこのアルゴリズムは入力配列の \(2^{n}\) 個の部分列全てを調べるからです。

最長増加部分列 テイク 2

最長増加部分列を見つけるのに使えるバックトラッキングを使ったアルゴリズムはこれだけではありません。入力配列を一つずつ走査していくのではなくて、出力配列を一つずつ構築していくこともできます。つまり、「\(A[i]\) は出力配列に含まれるか？」ではなく「出力配列における次の要素は何か？ そもそも存在するか？」を直接考えるということです。

この戦略を処理している途中に放り込まれた場合、次のような図を目にすることになります。黒いバーのすぐ左にある \(6\) がちょうど出力配列に入れられた要素であり、黒いバーより右にある要素のうちどれを次に出力配列に含まれるかをこれから決断することになります。

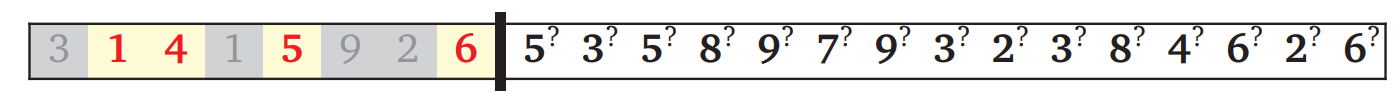
もちろん、バーより右にある数のうち \(6\) より大きいものだけを考えます。

これらの数字のうちどれを選べば良いか、私たちには何の手掛かりもありません。どの値が一番良いかを "賢く" 考えても話がこんがらがるだけなので、全ての選択肢を総当たりで試すことにします。それぞれの選択肢について、同じプロセスを再帰的に繰り返します:

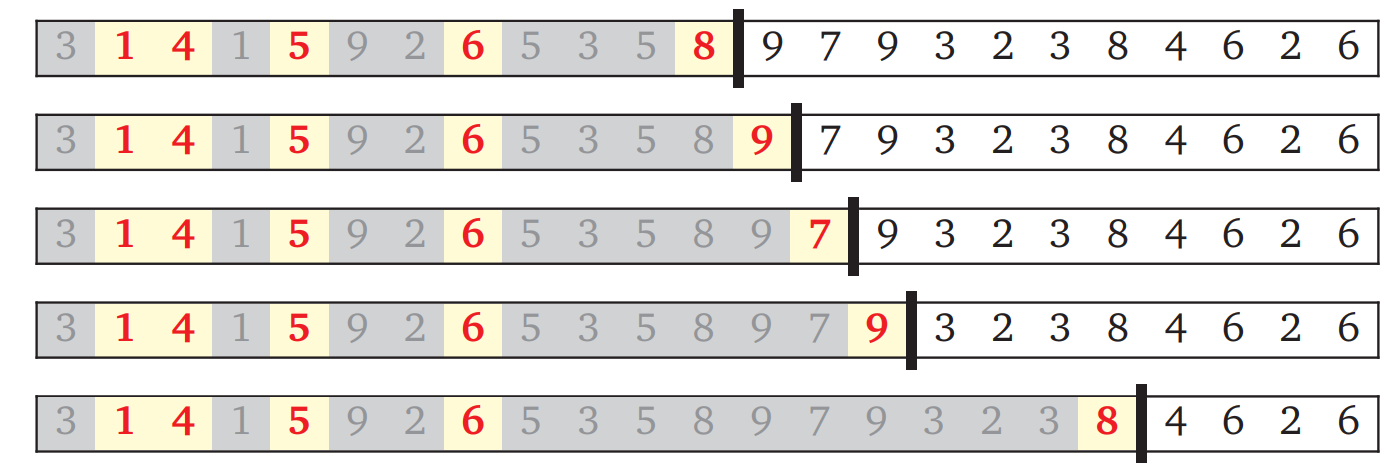
出力配列に次に入れる数の選択肢は、出力配列に最後に入れた数だけに依存します。そのため先ほどの図は処理が終わった部分を取り除いて単純化できます:

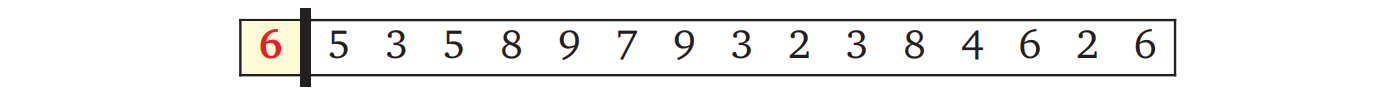
黒いバーの右側に残った数字は入力配列の接尾部分です。そのため、入力配列 \(A[1..n]\) をグローバル変数とすれば、再帰的な問題を添え字を使って次のように表せます:

\(A[i]\) で始まる \(A[i..n]\) の部分列の中で一番長いものを \(\mathit{LISFirst}(i)\) と表すことにすると、上述のバックトラッキングを使った再帰的な戦略から次の再帰的な方程式が得られます: \[ \mathit{LISFirst}(i) = 1 + \max \lbrace \mathit{LISFirst}(j)\ |\ j > i \text{ かつ } A[j] > A[i] \rbrace \] 自然数の集合を考えているので、\(\max \varnothing = 0\) と定義します。そうすれば「全ての \(j > i\) について \(A[j] \leq A[i]\)」ならば「\(\mathit{LISFirst}(i) = 1\)」であり、これがベースケースとなります。この再帰方程式を疑似コードで表すと、次のようになります:

最後に、このアルゴリズムを使って元々の問題を解きます。つまり、出力配列の最初の要素を知ることなく出力を計算します。最初の要素として全ての要素を総当たりで試すというのも一つのやり方ですが、入力配列の最初に門番 \(-\infty\) を追加してその門番から始まる最長増加部分列の長さを求め、最後に \(1\) を引くという方法もあります。両方の実装を示します:

最適二分探索木

この章で最後に説明するのは、再帰的なバックトラッキングと分割統治法を組み合わせた例です。

二分探索木の探索が成功した場合、その実行時間は探索する頂点の祖先¹³の数に比例することを思い出してください。このため探索の最悪実行時間は木の深さに等しくなります。したがって探索処理の最悪計算時間を小さくするには、木の高さは最小であるべきであり、理想は完璧にバランスの取れた木です。

しかし二分探索木が使われる多くの場合においては、重要となるのは最悪の場合の計算時間ではなくて、何度か行われる探索の平均実行時間であることが多いです。もし \(x\) が \(y\) よりも頻繁に探索されるのであれば、\(x\) を \(y\) よりも木の上の方に配置することで (たとえそれで木の深さが大きくなったとしても) 時間を節約できます。ある要素が他の要素に比べて格段に多く探索される場合、完全二分木は最適な形ではありません。深さが \(\Omega(n)\) の全くバランスの取れていない木が最適である可能性だってあります！

この状況は次の問題として定式化できます。すなわち、ソートされた鍵 (key) 配列 \(A[1..n]\) とそれに対応するアクセス頻度 (access frequency) \(f[1..n]\) が与えられ、鍵 \(A[i]\) が \(f[i]\) という頻度で探索されるときに、全体の探索時間を最小化する二分探索木を作る問題です。

解法を考える前に、この問題で最小化すべき再帰的な関数の定義を考えましょう。 頂点 \(v_{1}, v_{2}, \ldots, v_{n}\) を持つ二分探索木 \(T\) が与えられ、頂点の添え字は頂点 \(v_{i}\) が鍵 \(A[i]\) を保持するようにソートされているとします。このとき全ての頂点に対する二分探索の実行時間は、定数部分を無視すると次のように書けます: \[ \mathit{Cost}(T, f[1..n]) := \sum_{i=1}^{n} f[i] \cdot T \text{ における } v_{i} \text{ の祖先の数} \quad (*) \] \(v_{r}\) と \(T\) の根とすると、定義により \(v_{r}\) は \(T\) の全ての要素の祖先です。\(A\) がソートされていることから、\(i < r\) ならば \(v_{r}\) を除く \(v_{i}\) の祖先は全て \(T\) の左側の部分木に属します。同様に \(i>r\) ならば \(v_{r}\) を除く \(v_{i}\) の祖先は全て \(T\) の左の部分木に属します。よって、\(\mathit{Cost}\) 関数を次のように分割できます: \[ \begin{aligned} \mathit{Cost}(T, f[1..n]) := \sum_{i=1}^{n}f[i] & + \sum_{i = 1}^{r - 1} f[i] \cdot \mathit{left}(T) \text{ における } v_{i} \text{ の祖先の数} \\ & + \sum_{i = 1}^{r + 1} f[i] \cdot \mathit{right}(T) \text{ における } v_{i} \text{ の祖先の数} \end{aligned} \] 二番目と三番目の項は \(\mathit{Cost}\) の定義 \((*)\) と同じなので、この式をさらに変形して再帰方程式にできます: \[ \begin{aligned} \mathit{Cost}(T, f[1..n]) := \sum_{i=1}^{n}f[i] & + \mathit{Cost}(\mathit{left}(T), f[1..r-1]) \\ & + \mathit{Cost}(\mathit{right}(T), f[r+1..n]) \end{aligned} \] この再帰方程式に対するベースケースは、いつもと同じように、\(n = 0\) における \(\mathit{Cost} = 0\) です。空配列に対しては探索が全く行われず、時間消費が \(0\) だからです。

この \(\mathit{Cost}(T, f)\) 関数を最小化するような二分探索木 \(T_{opt}\) を作ることが目標となります。もし何らかのマジカルな方法で \(T_{opt}\) の根が \(v_{r}\) であると知ることができたならば、\(\mathit{Cost}(T, f)\) の定義から直ちに、部分木 \(\mathit{left}(T_{opt})\) が鍵 \(A[1..r-1]\) と頻度 \(f[1..r-1]\) に対する最適二分探索木であることが分かります。同様に、 \(\mathit{right}(T_{opt})\) は鍵 \(A[r+1 .. n]\) と頻度 \(f[1..r-1]\) に対する最適二分探索木であることも分かります。つまり、最適木の根さえ正しく選択すれば、残りは再帰の妖精が作ってくれます。

もっと一般的に言えば、\(\mathit{OptCost}(i, k)\) を頻度 \(f[i..k]\) に対応する最適二分探索木の探索時間の和としたとき、この関数は以下の再帰方程式に従います: \[ \mathit{OptCost}(i, k) = \begin{cases} 0 & \text{if } i > k \\ \displaystyle \sum_{j=i}^{k}f[j] + \min\limits_{i \leq r \leq k} \left \lbrace \begin{array}{l} \mathit{OptCost}(i, r-1) \\ \ + \mathit{OptCost}(r+1, k) \end{array} \right \rbrace & \text{それ以外} \end{cases} \] ベースケースは空配列に対する探索がゼロ時間で終わることを表します。元々の問題に対する答えは \(\mathit{OptCost}(1, n)\) となります。

この再帰的な定義を使えば、\(\mathit{OptCost}(1, n)\) を計算するバックトラッキングを使った再帰的アルゴリズムが機械的に書けます。驚くことではありませんが、このアルゴリズムの実行時間は指数時間です。次の章ではこの実行時間を多項式時間に抑える方法について見るので、ここで正確な実行時間を求めることにはあまり意味がありません...

❤ 解析

...あなたが興味を持っていない限りは。面白そうなので、このバックトラッキングを使ったアルゴリズムがどれだけ遅いかを正確に計算してみましょう。実行時間は次の再帰方程式を満たします: \[ T(n) = \sum_{k=1}^{n}(T(k - 1) + T(n - k)) + O(n) \] ここで \(O(n)\) の項は探索の回数 \(\sum_{i=1}^{n} f[i]\) を求めるための時間です。ぎょっとするような方程式ですが、前に使った引き算によるテクニックをここでも使うことができます。\(O()\) 表記を明示的な定数で置き換え、式を整理して、\(T(n) - T(n-1)\) を計算して和を消し、最後にまた整理します: \[ \begin{aligned} T(n) & = 2\sum_{k=0}^{n-1} T(k) + \alpha n \\ T(n-1) & = 2\sum_{k=0}^{n-2} T(k) + \alpha (n-1) \\ T(n) - T(n-1) & = 2T(n-1) + \alpha \\ \therefore T(n) & = 3T(n-1) + \alpha \end{aligned} \] これなら何とかできそうです。再帰木を使うと \(\pmb{T(n) = O(3^{n})}\) が分かります (帰納法を使っても確認できます)。

この解析によると、この再帰的なアルゴリズムは全ての二分探索木を検査するわけではありません！なぜなら、 \(n\) 個の頂点を持つ二分探索木の数 \(N(n)\) は再帰方程式 \[ N(n) = \sum_{r=1}^{n-1}(N(r - 1) \cdot N(n - r)) \] を満たし、この解は \(N(n) = \Theta(4^{n} / \sqrt{n})\) だからです (この解は自明ではありません)。最適二分探索木を求めるアルゴリズムは、左右の部分木を独立に調べることによって大きく時間を節約しています。二分探索木に対する総当たりを行うと左右の部分木を組で考えることになり、余計に時間がかかります。これは \(N(n)\) が満たす方程式に積が含まれていることからも分かります。

練習問題

1. このゲームが何と呼ばれているか、および私が覚えているルールが正しいかどうかは分かりません。このゲーム (あるいはこのゲームに似たもの) は Lenny Pitt に教わりました。彼はレストランにおいてある人工甘味料の袋 (fake-sugar packet) でこのゲームをやることを勧めていました。^[return]

2. Constantin Fahlberg (コンスタンティン・ファールベルク) と Ira Remsen (アイラ・レムセン) は 1878 年に世界で初めてサッカリンを合成しました。このとき Fahlberg はコールタールの誘導体について研究する Remsen の研究室のポスドクでした。1900 年、Ovidio Rebaudi (オヴィディオ・レバウディ) は ka'a he'ê という植物についての世界で初めての化学的な解析を発表しました。この植物はグアラニー族で 1500 年以上にわたって栽培されてきた薬草で、現在ではステビア (Stevia rebaudiana) という名前で知られています。^[return]

3. もしあるなら、どこで知ったのかぜひ教えてください！^[return]

4. Zermelo が考えたゲームのクラスは有限の状態を持ちますが、手の列が無限に伸びることを許していたので、ここに示したものよりもう少し複雑です (Zermelo は無限に続くゲームを引き分けと定義しました)。^[return]

5. ヒューリスティックとは正しく動かないアルゴリズムのことを言います (ただし実用上はうまく動きます。たまに、見かけ上は)。^[return]

6. 他のどの値になると言うのです？^[return]

7. この独立性の条件を満たさないゲームはたくさんあります。例えば一般的なチェスとチェッカーのルールでは同じ盤面が三回続いた場合には引き分けとしてもよいことになっており、中国式の囲碁ではそれまでの盤面を繰り返すような手を禁止しています。このようなゲームについては、ゲームの状態に現在の盤面だけではなくそれまでの全ての打ち手の記録が含まれます。^[return]

8. 古典ラテン語の・たいていの・写本は・ interpunct と・呼ばれる・小さな点を・使って・単語の・区切りを・表して・いました。しかし scriptio continua が好まれたことで、紀元三世紀ごろには interpunct はほとんど見られなくなりました。単語の間に空白を入れる記法はアイルランド人の僧侶達によって八世紀ごろに導入され、数世紀をかけて少しずつヨーロッパ全体に広がっていきました。 scriptio continua は二十一世紀の英語でも URL とハッシュタグに生き残っています。 #octotherps4lyfe^[return]

9. 大雑把に翻訳すると: 「まず、そのような取るに足らない知識に品位などありえない。そんな知識は自明なことであって、ほとんどが個々の文字と単語の間の点の配置に関するものである」Cicero は彼の友人 (！) の法律に関する専門知識を公然と侮辱しています。このあと彼は、領事の選挙で敗れた Murena を贈賄の罪で訴えていた法学者 Servius Sulpicius Rufus (セルウィウス・スルピキウス・ルフス) に言及します。Cicero の鋭い弁護によって、ほぼ間違いなく有罪だった Murena は無罪を勝ち取りました。 #librapondo #nunquamestfidelis^[return]

10. St. Augustine による De doctrina Christiana には、句読点を入れることでラテン語聖書から曖昧さを取り除くことだけについて書かれた章があります。^[return]

11. 正確なことを言うと、 \(\textsc{IsWord}\) が多項式時間で実行される限り、 \(\textsc{Splittable}\) は \(O(2^{n})\) 時間で実行されます。^[return]

12. アルファベットをランダムに並べた文字列のほとんどは英単語ではないために、文字列を英単語ごとに分割する問題でこの仮定をすると、実行時間が実際よりもとても大きく見積ることになります。しかし英語の単語列を文法的に正しい英語の文に分割する問題ではそうではありません。例えば正の整数 \(n\) について \(n\) 個の "buffalo" や \(n\) 個の "police"、\(n\) 個の "can" が並んだ単語列を考えてみてください (At the Moulin Rouge, dances that are preservable in metal cylinders by other dances have the opportunity to fire dances that happen in prison restroom trash receptacles.)。^[return]

13. 頂点 \(v\) の祖先 (ancestor) とは、その頂点と \(v\) の親の祖先を合わせたものです。 \(v\) の真の祖先 (proper ancestor) とは、 \(v\) の親と \(v\) の親の真の祖先を合わせたものです。^[return]

14. これに対して Sedgewick の提案したデータ構造は右の子が赤くないという制約を持っていました。奇妙なことに、Andersson と Sedgewick は両人とも卵をどちら側から食べるかについては沈黙したままです。^[return]