NP 困難性
短い取っ散らかった論文の中で、彼 [アリストテレス] は不変的な意味を持つ手本を示した。それは何かの法則の手本ではないし、何かの方法論の手本でもない ――方法論はとても高度に発展した知性によってのみ作られるからだ。彼が示したのは、感覚を鋭く分析して原則あるいは定義を引き出すという、知性そのものの手本である。
規格の何が良いかというと、選択肢が増えることだ。さらに、今ある規格のどれも気に入らないなら、来年のモデルを待つこともできる。
ここに存在しない物を誰の目にも明らかなように示すのには実は優れた知性が必要となる。「自分にも考え付くことができたのに」という嘆きは本当によく聞かれるが、的を外している。そのように嘆く人々は考え付かなかったのであり、だからこそ明らかになった事実は重要で意義深いのである。
問題に答えが無いのなら、それは問題ではなくて事実なのかもしれない ――
解決するものではなくて、時間をかけて付き合うものなのかもしれない。
勝てないゲーム
赤いスーツに身を包んだ、Tom Waits よろしくいかつい顔をしたセールスマンが、\(n\) 個のスイッチと一つの電球の付いた黒い金属の箱をあなたに見せてきました。セールスマンによると、箱の中にはブール回路 ――たくさんの \(\textsc{And}\), \(\textsc{Or}\), \(\textsc{Not}\) を繋いだもの―― が入っており、その回路の入力が \(n\) 個のスイッチで、出力が電球であるとのことです。
そして彼は次の質問をしました: 「電球を灯らせる入力は存在するか?」もし質問に正しく答えることができたら、あなたはその箱と 一億 一兆ドルを入手でき、答えが間違っていた場合および答えを出すことなくあなたが死亡した場合には、彼があなたの魂を奪うと言います。

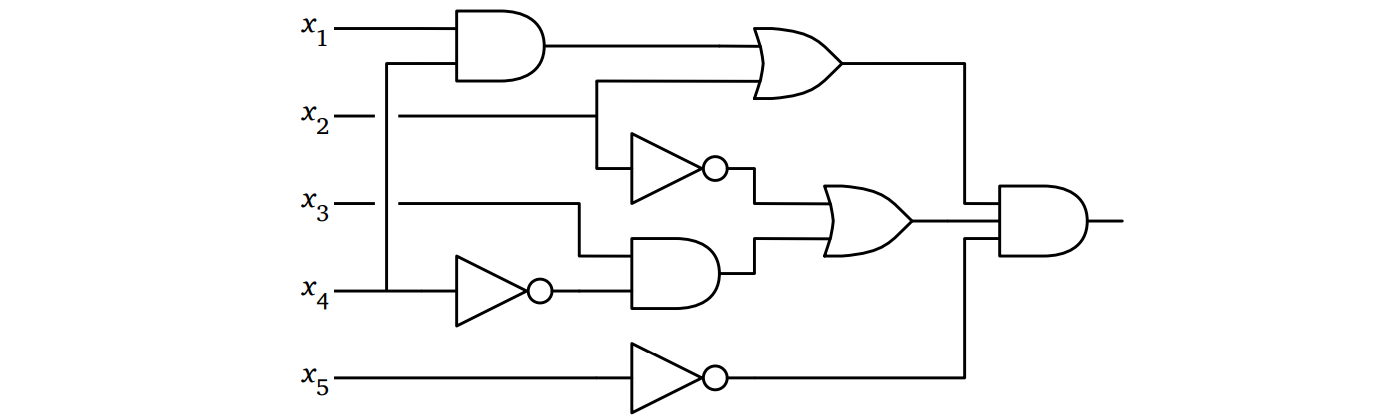
見たところ、敵はまだどのスイッチも電球に繋いでいないようです。そのためどうスイッチを動かしたとしても電球が灯ることはありません。もしあなたが「明かりを灯すことができる」と答えた場合、敵は箱を開けて回路が何も無いことを見せるでしょう。しかしもしあなたが \(2^{n}\) 個のスイッチの設定を全て試す前に「明かりを灯すことはできない」と答えた場合、敵は魔法の力であなたがまだ試していない設定に限って明かりがつくような回路を作成し、スイッチをその設定にして明かりを灯して見せるでしょう (答えが敵によって確認されるまでは箱の中を見ることはできないので、敵がインチキをしているのを見破ることはできません)。
敵の質問に証明付きで正しく答えるには、実際に \(2^{n}\) 個の設定を全てを試すしかありません。しかしこうすると問題を解くのにあなたの人生よりもはるかに長い時間が必要になることは明らかなので、あなたは敵のオファーを礼儀正しく断ることになります。
敵は一カートンのマルボロを吸ってから、微笑んで、Heath Ledger 演じるジョーカーのようなどすの利いた声で言います「えぇ、もちろん、あなたは私のことなんて信じない。でも、こうすれば安心でしょう」 彼は特大の羊皮紙 ――本当に羊の皮からできているといいのですが―― をあなたに手渡しました。そこには回路図が書かれています。おそらく彫られているのでしょう。「それは箱の中にある回路の回路図だ。箱の中を見てその図の通りに回路が組まれているか調べてもらって構わない。あるいは回路図から実際の回路を作ってもいいし、コンピューターを使ってシミュレーションをしてもいい。何をしてもいい。もしその回路図が箱の中にある実際の回路と違っていると示せたら、そのときも一兆ドルを渡そう」いくつかの設定を調べてみたところ、どうやら回路図に間違いはないようです。また小細工も不可能に見えます。
しかしこの "気前の良い" オファーもまた断るべきです。敵が示した問題は回路充足問題 (circuit satisfiability problem) または \(\textsc{CircuitSAT}\) と呼ばれます。つまり、与えられられたブール回路の入力で回路の出力が \(\textsc{True}\) になるものが存在するかを判定する問題です。全ての入力に対して \(\textsc{False}\) を返すかどうかを判定する問題とも言えます。
特定の入力に対する出力の計算は深さ優先を使うことで多項式時間で (実は線形時間で) 行えます。しかし \(\textsc{CircuitSAT}\) に対する \(2^{n}\) 個の入力全てを考える場合には、指数時間を使って総当たりで試すよりも速く解く方法を知っている人は誰もいません。確かに、総当たりよりも高速にはできないときちんと証明した人は誰もいません ――なのでもしかしたら、万が一には、まだ発見されていない賢いアルゴリズムがあるのかもしれません―― が、反重力ユニコーンが存在しないときちんと証明した人もいないのです。現実世界で私たちが解くことになるデータに対しては、\(\textsc{CircuitSAT}\) に対する高速なアルゴリズムは存在しないと思った方が安全でしょう。
セールスマンに No を伝えると、彼は微笑んでから「見た目よりは賢いようだな、小僧」と言って、反重力ユニコーンに乗って飛び去って行きましたとさ。
P 対 NP
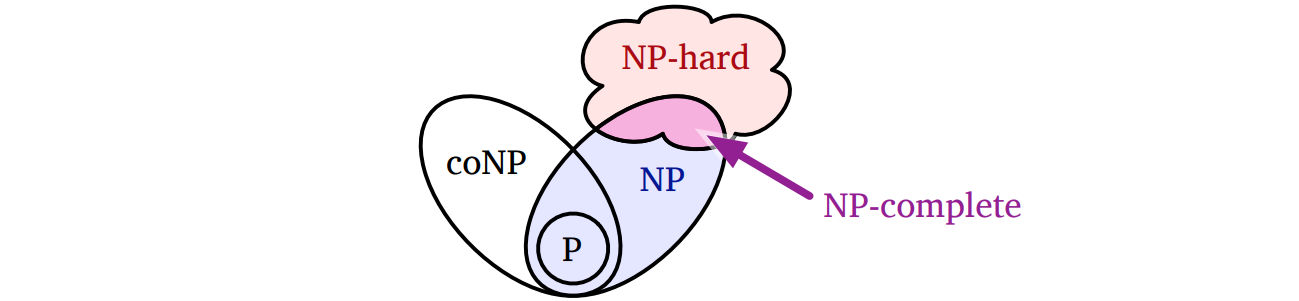
アルゴリズムが "効率的である" ための最低条件は、実行時間が入力サイズの多項式で抑えられることです。つまり入力サイズを \(n\) としたときにある定数 \(c\) が存在して、実行時間が \(O(n^{c})\) となるということです1。研究者達は全ての問題が高速に解けるわけではないことに早くから気付いていましたが、どの問題が早く解けてどの問題がそうでないのかを見極めるのに苦労していました。NP 困難 (NP-hard) と呼ばれる問題は誰もが多項式時間で解けないと信じているものの、実行時間の下限が超多項式的になることは誰も証明できていません。
判定問題 (decision problem) とは出力が一つの真偽値 (\(\textsc{Yes}\) か \(\textsc{No}\)) であるような問題のことです。判定問題のクラスを三つ定義します:
-
P は多項式時間で解ける判定問題からなる集合です。直感的には、\(P\) は高速に解ける判定問題の集合です。
-
NP は「もし答えが \(\textsc{Yes}\) ならば、そのことを多項式時間で確認できる証明 (proof) が存在する」という特徴を持つ問題の集合です。直感的には、NP は答えが \(\textsc{Yes}\) ならばそれを高速に検証できる判定問題の集合です。
-
co-NP は NP の逆です。co-NP に属する問題の答えが No ならば、多項式時間でそのことを検証できる証明が存在します。
例として、回路充足問題が NP に属するかどうかを考えてみます。もし回路が充足可能ならば、その回路を充足させる任意の \(m\) ビットの入力を受け取って実際に回路を評価することで、充足可能性を多項式時間で確認できます。したがってこのような入力が証明となるので、回路充足問題は NP に属します。回路充足問題は P にも co-NP にも属さないと広く信じられていますが、本当のところは誰にもわかりません。
P に属する全ての判定問題は NP にも属します。なぜならもし問題が P に属しているなら、\(\textsc{Yes}\) という答えは最初から問題を解くことで多項式時間で確認できるからです!同様の理由で P に属する全ての問題は co-NP にも属します。
科学、いや情報科学、いや理論情報科学における未解決問題の中で最も重要な問題を一つあげるとすれば、それは複雑性クラス P と NP が本当に異なっているのかという問題です。ほとんどの人にとって P \(\neq\) NP は直感的に明らかです。アルゴリズムとデータ構造に関する講義で課題や試験に取り組んだことがあるなら、たとえ後から見れば簡単に解ける問題であったとしても、初見のアルゴリズムの問題を解くのは難しいと分かっているでしょう (分かっていることを願います)。また問題をゼロから解くことが、一つの解答が正しいかをチェックすることより難しいのは完全に明らかです。"P \(\neq\) NP" という命題を自然法則として受け入れても何ら不都合は生じないでしょう ――実際多くのアルゴリズム設計者は受け入れています。つまり、P \(\neq\) NP が Maxwell 方程式や相対性理論、あるいは太陽が明日昇ることと同じように証拠によって支えられていて、数学的には証明されていないということです。
一方でもし数学的に厳密になるなら、どうやって P \(\neq\) NP を証明すべきかさえ誰にも分かっていないということを認めなければなりません。実は、証明に向けた進展は何十年にもわたってほとんどあるいは全くありません2。クレイ数学研究所は P 対 NP 問題を七つのミレニアム懸賞問題の一つとしており、解答を示した人物に対する $1,000,000 の賞金を用意しています。そしてこの問題を解こうして魂を (とまではいかなくても、少なくとも正気を) 失ってしまった人もいます。
複雑性クラス NP と co-NP が異なるのかというより細かい問題もまた未解決です。\(\textsc{Yes}\) という答えを高速に検証できるからといって \(\textsc{No}\) の答えも高速に検証できるとは限らないということです。例えば現在分かっている限りでは、回路が充足できないことに対する短い証明は存在しません。一般的には NP \(\neq\) co-NP と信じられていますが、この命題もどうやって証明すべきかは誰にも分かりません。

NP 困難・NP 容易・NP 完全
問題 \(\Pi\) がNP 困難 (NP-hard) であるとは、\(\Pi\) に対する多項式時間合アルゴリズムが NP に属する全ての問題に対する多項式時間アルゴリズムを意味することを言います。言い換えると:
分かりやすく言うと、ある NP 困難な問題 \(\Pi\) が一つでも高速に解ければ、 \(\Pi\) を解くサブルーチンを使うことで、答えが簡単に検証できる種類の問題全てを高速に解くことができるということです。NP 困難な問題は少なくとも NP に属する全ての問題以上に難しいと言えます。
そして問題が NP 完全 (NP complete) であるとは、NP 困難かつ NP に属する ("NP 容易である") ことを言います。くだけて言うと、NP 完全な問題とは NP の中で一番難しい問題です。ある NP 完全な問題に対する多項式時間アルゴリズムがあれば、全ての NP 完全な問題に対する多項式時間アルゴリズムが直ちに手に入ります。数千個もの問題が NP 完全であると示されているので、その中のある一つの問題に対する (そして全ての問題に対する) 多項式時間アルゴリズムというのはまずありえなさそうに思えるわけです。
ある問題が NP 困難であると示すのは、「もし私が犬を飼っているなら、私の犬は英語を流暢に話す」と言うようなものです。私が犬を飼っているかあなたには分からないでしょうが、英語を話す犬を飼っていないことは分かるはずです。犬が英語を話せないことの数学的な証明はありません ――英語を話す犬を誰も見たことがないこと、あるいは犬に英語を話すための器官や脳が足りていないことを示すたくさんの研究結果も証拠に過ぎず、証拠だけでは数学的な証明にはならないからです。しかしもちろんまともな人間ならば私が流暢に英語を話す犬を飼っているとは信じないので、「もし私が犬を飼っているなら、私の犬は英語を流暢に話す」という文章からは、「まともな人間は私が犬を飼っているとは信じない」という系が得られます! 同様に、ある問題が NP 困難ならば、まともな人間はその問題が多項式時間で解けるとは思いません。
どんな問題であれ、その問題が NP 困難かどうかは自明ではありません。次に示す重要な定理は 1971 年に Steve Cook (スティーブ・クック) によって発表され、その後 1973 年には Leonid Levin (レオニード・レビン) によって独立に示されています3。ここまで定義を (意図的に) 曖昧に書いてきたので、証明は省略します4。
Cook-Levin の定理: 回路充足問題は NP 困難。
❤ きちんとした定義 (HC SVNT DRACONES)
複雑性クラス P, NP, co-CP をきちんと定義するには、言語 (language) と Turing 機械を使った議論が必要です。言語とは有限アルファベット \(\Sigma\) 上の文字列の集合であり、\(\Sigma = \lbrace {\color{maroon}{0}}, {\color{maroon}{1}} \rbrace\) と仮定しても一般性は失われません。Turing 機械とは機能が極端に制限されたコンピューターであり、その詳細な定義は計算能力を考えるときには驚くほど重要ではありません。
P は決定性単一テープ Turing 機械を使って多項式時間 (polynomial time) で判定できる言語の集合として定義されます。同様に NP は非決定性 Turing 機械を使って多項式時間で判定できる言語の集合として定義されます。NP は Nondeterminitic Plynomial-time (非決定性多項式時間) の略です。
多項式時間という条件は十分大雑把なので、Turing 機械の正確な形式はどんなものであっても構いません (テープの数、ヘッドの数、トラックの数、アルファベットの数などが違っていても問題ありません)。実際、ランダムアクセス機械5において \(T(n)\) 時間で実行される任意のアルゴリズムは、単一テープ、単一トラック、単一ヘッド の Turing 機械を使って \(O(T(n)^{4})\) 時間でシミュレートできます。このシミュレーションが存在するおかげで、私たちが普段使うような for ループや再帰と言った高レベルなプログラミングの構文を使っても計算複雑性をきちんと議論できます。Turing 機械の言葉を直接使ってアルゴリズムを説明する必要はありません。
正確な定義において問題 \(\Pi\) が NP 困難であるとは、全ての問題 \(\Pi^{\prime} \in \text{NP}\) について \(\Pi^{\prime}\) から \(\Pi\) への多項式時間 Turing 帰着 (Turing reduction) が存在することとして定義されます。ここで Turing 帰着とは、Turing 機械で実行できる帰着のことです: つまり、\(\Pi\) を解く Turing 機械 \(M^{\prime}\) をブラックボックスなサブルーチンとして使って \(\Pi^{\prime}\) を解く Turing 機械 \(M\) のことです。Turing 帰着は神託帰着 (oracle reduction) とも呼ばれ、多項式時間 Turing 帰着は特に Cook 帰着と呼ばれます。
複雑性理論の研究者が NP 困難性を定義するときには多対一帰着 (many-one reduction) を使うことが多いです (多対一帰着は Karp 帰着とも呼ばれます)。ある言語 \(L^{\prime} \subseteq \Sigma^{\ast}\) から別の言語 \(L \subseteq \Sigma^{\ast}\) への多対一帰着とは、関数 \(f: \Sigma^{\ast} \rightarrow \Sigma^{\ast}\) であって \(x \in L^{\prime}\) \(\iff\) \(f(x) \in L\) となるものを言います。多対一帰着を使った場合、言語 \(L\) が NP 困難であることは、任意の言語 \(L^{\prime} \in \text{NP}\) 対して \(L^{\prime}\) から \(L\) への多項式時間で計算できる多対一帰着が存在することとして定義されます。
任意の Karp 帰着は Cook 帰着にできます。つまりある判定問題 \(\Pi\) から別の判定問題 \(\Pi^{\prime}\) への Karp 帰着が存在する場合には、その帰着を使って \(\Pi\) への入力を \(\Pi^{\prime}\) への入力に変換し、\(\Pi^{\prime}\) のオラクル (サブルーチン) を起動してその結果を返すという Cook 帰着が作れるということです。しかし現在分かっている限りでは全ての Cook 帰着が Karp 帰着でシミュレートできるわけではないので、逆は成り立ちません。
複雑性理論の研究者が Karp 帰着を好む主な理由は、 NP が Karp 帰着について閉じているのに対して Cook 帰着については閉じていないためです (NP=co-NP ならば Cook 帰着についても閉じますが、そうではないと考えられています)。(1) Cook 帰着を使った場合には NP 困難だが、(2) Karp 帰着を使った場合には P=NP のときに限って NP 困難となる、という二つの条件を満たす自然な問題が存在します。\(\textsc{UnSAT}\): 「与えられた論理式は常に偽か?」が明らかな例です。
また多対一帰着は判定問題 (正確に言うと判定 "言語") だけに対して定義されます。そのため厳密に言えば、Karp-NP 困難な最適化問題あるいは構成問題というものは存在しません。
さらに紛らわしいことに、Cook と Karp は両者とも NP 困難性を対数空間 (logarithmic-space) 帰着を使って定義していました。任意の対数空間帰着は多項式時間帰着ですが、(現在分かっている限り) 逆は成り立ちません。Cook 帰着と Karp 帰着の定義を対数空間帰着から多項式時間帰着に緩和したときに NP 困難な問題の集合が変化するのかどうかは未解決の問題です。
幸運にも、実際の問題においてこれまで述べてきた細かいことが頭をもたげることはありません。特にこの本で紹介される全ての帰着アルゴリズムは対数空間の多対一帰着にできます。ですから、ほら、もう目を覚ましてください。
帰着と SAT
回路充足性問題以外の全ての問題に対する NP 困難性を証明するには、帰着を使った議論が必要になります。問題 A を別の問題 B に帰着させる (reduce problem A to anther problem B) とは、問題 B へのアルゴリズムが手に入っているという仮定の下で問題 A を解くアルゴリズムを説明することを言います。帰着はこの本を読み始める前にも何度も行ってきたはずですが、そのときには帰着のことを「サブルーチンを書く」あるいは「ユーティリティ関数を書く」または「モジュール性の高いプログラムを書く」ときには「電卓を使う」などと呼んでいたでしょう。ある問題が NP 困難であることを示すときにもこれと同じような問題の間の変形を行いますが、ほとんどの人が想像する方向とは逆方向の変形を行います。
次の文章をタトゥーにして、腕の内側、ママの誕生日とモノポリーの本当のルール6の横に刻んでおくべきです。
つまり、ある問題が難しいことを示すには、その問題を効率良く解く正体不明のアルゴリズムをブラックボックスのサブルーチンとして仮定して、難しいことが前もって分かっている別の問題を解くアルゴリズムを示すことになります。ここで本質的に使われている論理は背理法による証明です。つまり、もし考えている問題が簡単ならもう一方の問題も簡単だと帰着が示しているのですが、それはあり得ないと最初から分かっているということです。同じことを言い換えると、もう一方の問題が難しいと分かっているので、帰着によって今考えている問題も難しい、つまり仮定として置いた効率の良いアルゴリズムは存在しないと示されるのです。
単純で重要な例として、式充足性問題 (formula satisfiability problem, \(\textsc{SAT}\)) を考えます。\(\textsc{SAT}\) の入力は次のようなブール式: \[ (a \lor b \lor c \lor \overline{d}) ⇔ ((b \land \overline{c}) \lor \overline{(\overline{a} ⇒ d)} \lor (c \neq a \land b)) \] であり、出力はこの式の変数 \(a, b, \ldots, \) に真偽値を割り当てて式全体を \(\textsc{True}\) にできるかどうかです。
\(\textsc{SAT}\) が NP 困難であることを示すには、既知の NP 困難な問題からの帰着を示す必要があります。私たちがこれまでに NP 困難であることを見た問題は \(\textsc{CircuitSAT}\) だけなので、そこから始めましょう。
\(K\) を任意のブール回路とします。\(K\) の各ゲートに新しい変数を割り当てて、ゲートごとに入出力を \(=\) でつないだ式をさらに \(\textsc{And}\) でつなげば \(K\) をブール式に変換できます。次の図にこの例を示します。
続いて元の回路 \(K\) の充足可能性とこの変換で得られる式 \(\Phi\) の充足可能性が同値であることを示します。同値性の証明でよくあるように、証明は二つのステップからなります:
-
\((\Rightarrow)\) \(K\) を充足させる入力が与えられれば、\(K\) の各ゲートにおける出力の値を計算することで \(\Phi\) を充足させる変数への真偽値割り当てを得られる。
-
\((\Leftarrow)\) \(\Phi\) を充足させる変数割り当てが与えられれば、中間の変数 \(y_{i}\) と最終的な出力 \(z\) を無視することで \(K\) を充足させる入力を得られる。
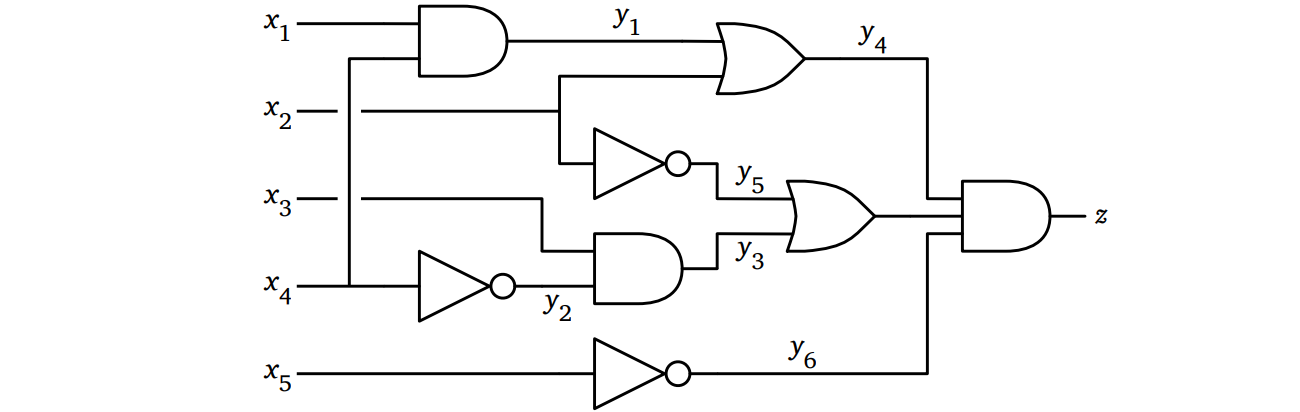
回路からブール式への変換は線形時間で行うことができ、変換結果のブール式の大きさは常識的な方法で表された回路の大きさの高々定数倍です。
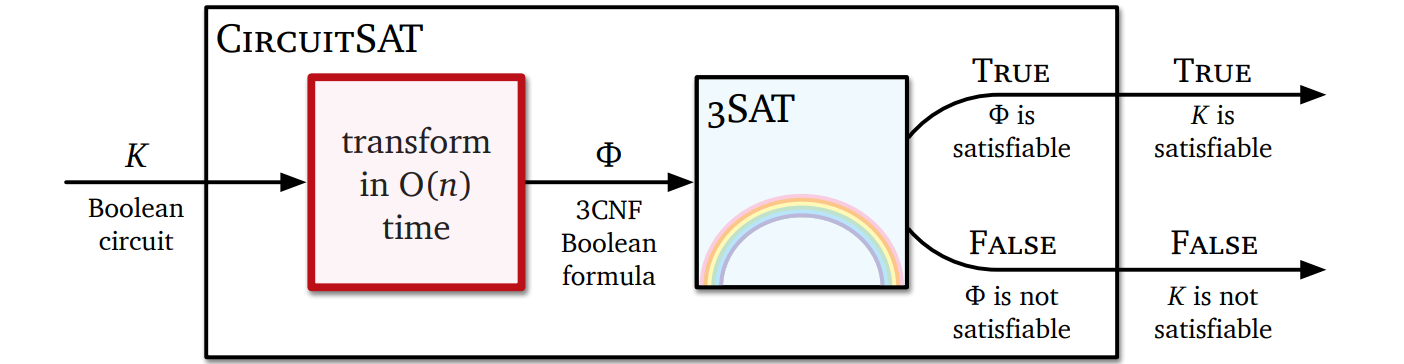
与えられたブール式が充足可能かどうかを多項式時間で判定するアルゴリズムが存在すると仮定します。このときブール回路 \(K\) が与えられれば、上記の方法で \(K\) をブール式 \(\Phi\) に変形し、この \(\Phi\) に対してその正体不明の \(\textsc{SAT}\) アルゴリズムを適用することで、\(K\) が充足可能かどうかを判定できます。
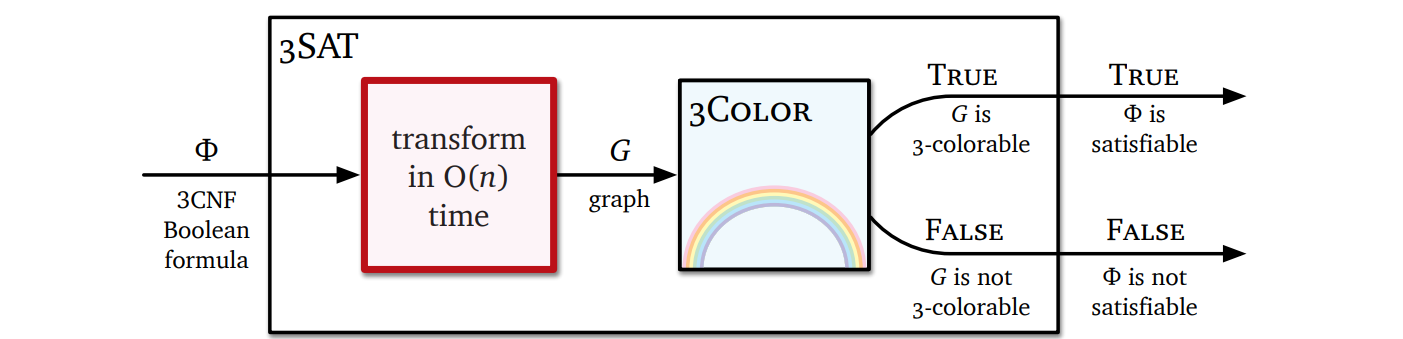
この処理を次の図に示します。四角がアルゴリズムを表し、左の赤い四角が変形のためのサブルーチンを、右の水色の四角が正体不明の \(\textsc{SAT}\) アルゴリズムを表します。虹がかかっているのですから、魔法の箱に決まっています7。
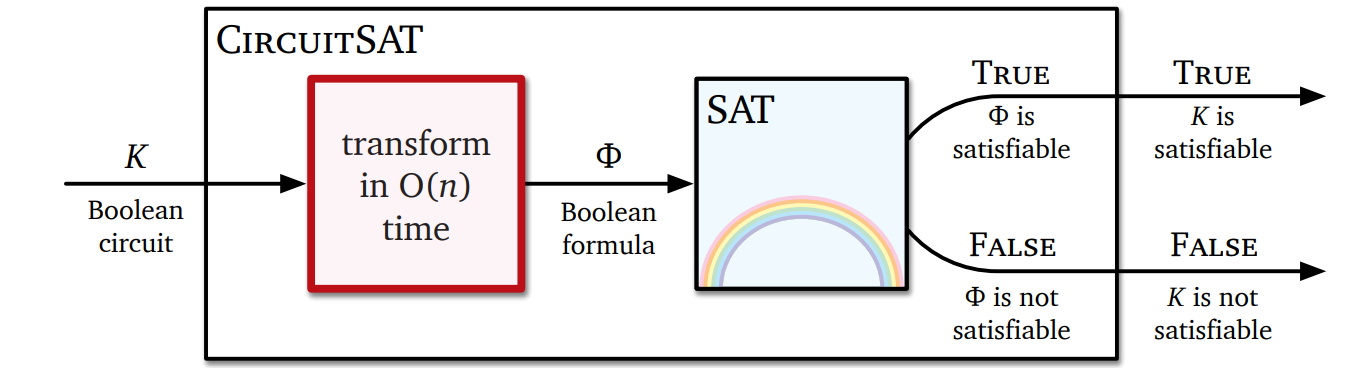
魔法の箱ではなく魔法の疑似コードがお好みなら:
procedure \(\texttt{CircuitSAT}\)(\(K\))
\(K \text{ をブール式 } \Phi \text{ に変換する}\)
return \(\texttt{SAT}\)(\(\Phi\)) \({\color{maroon}\langle \langle} *** \color{orange}{M} \color{olive}{A} \color{green}{G} \color{teal}{I} \color{#2D2F91}{C} *** {\color{maroon}\rangle \rangle}\)
\(K\) を \(\Phi\) に変換する処理は多項式時間で行える (本当は線形時間なのですが、多項式時間でできることは確かな) ので、\(\textsc{CircuitSAT}\) アルゴリズム全体も多項式時間で実行できます: \[ T_{\textsc{CircuitSAT}}(n) \leq O(n) + T_{\textsc{SAT}}(O(n)) \] よって \(\textsc{SAT}\) に対する多項式時間アルゴリズムがあれば \(\textsc{CircuitSAT}\) に対する多項式時間アルゴリズムが手に入り、したがって P=NP です。すなわち \(\textsc{SAT}\) は NP 困難です!
3 SAT (CircuitSAT からの帰着)
様々な問題の NP 困難性を証明するのに特に便利な \(\textsc{SAT}\) の特殊ケースがあり、\(\textsc{3CNF-SAT}\) あるいは \(\textsc{3SAT}\) と呼ばれます。
ブール式が連言標準形 (conjunctive normal form, CNF) であるとは、式がいくつかの節 (clause) の連言 (disjunction, \(\textsc{Or}\)) であり、それぞれの節がリテラルの選言からなる (conjunction, \(\textsc{And}\)) ことを言います。ここでリテラルは一つの変数またはその否定です。例えば: \[ \overbrace{(a \lor b \lor c \lor d)}^{\text{節 (clause)}} \land (b \lor \overline{c} \lor \overline{d}) \land (\overline{a} \lor c \lor d) \land (a \lor \overline{b}) \] は CNF 式です。3CNF 式とは 全ての節が三つのリテラルからなる CNF 式のことです。上の式では最初の節にはリテラルが 4 つ、最後の節にはリテラルが 2 つあるので 3SAT ではありません。3CNF 式が与えられたときに、その式が \(\textsc{True}\) に評価されるような変数への真偽値割り当ては存在するでしょうか?
\(\textsc{3SAT}\) を一般的な \(\textsc{SAT}\) からの帰着で示すこともできますが、\(\textsc{CircuitSAT}\) からの帰着を作って "最初から" 示した方が簡単です。
任意のブール回路 \(K\) が与えられたとき、次に示すステージを経ることで \(K\) を同値な 3CNF 式に変換できます。各ステージを説明すると同時にその正しさの証明も行います。
-
\(K\) が \(k > 2\) 個の入力を持つゲートがある場合には、そのゲートを \(k - 1\) 個のゲートからなる二分木に置き換えることで、全ての \(\textsc{And}\) ゲートと \(\textsc{Or}\) ゲートの入力の数を二つにする。置き換えた後の回路を \(K^{\prime}\) とすると、\(K\) と \(K^{\prime}\) は論理的に同値な回路だから、\(K\) を充足させる入力は \(K^{\prime}\) も充足させ、その逆も成り立つ。
-
前節で \(\textsc{SAT}\) の帰着に用いたのと同じ方法を使って、各ゲートが一つの節に対応するように \(K^{\prime}\) をブール式 \(\Phi_{1}\) に変形する。\(K^{\prime}\) を充足させる入力は \(\Phi_{1}\) を充足させる入力に変換できることおよびその逆は前に示した。
-
\(\Phi_{1}\) に含まれる全ての節を CNF 式に置き換える。\(\Phi_{1}\) が持つ節の形は \(K^{\prime}\) のゲートの種類に対応して三種類だけであり、それぞれ次のように変換できる: \[ \begin{aligned} a = b \land c & \longmapsto (a \lor \overline{b} \lor \overline{c}) \land (\overline{a} \lor b) \land (\overline{a} \lor c) \\ a = b \lor c & \longmapsto (\overline{a} \lor b \lor c) \land (a \lor \overline{b}) \land (a \lor \overline{c}) \\ a = \overline{b} & \longmapsto (a \lor b) \land (\overline{a} \lor \overline{b}) \end{aligned} \] こうして出来上がる CNF 式を \(\Phi_{2}\) とする。\(\Phi_{1}\) と \(\Phi_{2}\) は論理的に同値な式だから、\(\Phi_{1}\) を充足させる入力は \(\Phi_{2}\) も充足させ、その逆も成り立つ8。
-
\(\Phi_{2}\) の各節を 3CNF 式に置き換える。\(\Phi_{2}\) の各節は最大でも三つのリテラルを持つので、三つのリテラルを持つ節はそのままにし、それ以外の二種類の節は次のように展開する。展開のときには新しい変数が導入される: \[ \begin{aligned} a \lor b & \longmapsto (a \lor b \lor x) \land (a \lor b \lor \overline{x}) \\ a & \longmapsto (a \lor y \lor x) \land (a \lor \overline{y} \lor x) \land (a \lor y \lor \overline{x}) \land (a \lor \overline{y} \lor \overline{x}) \end{aligned} \] 最終的に出来上がる 3CNF 式を \(\Phi_{3}\) とする。\(\Phi_{2}\) を充足させる任意の入力は、新しい変数 (\(x\) と \(y\)) にどんな値を割り当てても \(\Phi_{3}\) を充足させる入力となる。逆に \(\Phi_{3}\) を充足させる任意の入力の新しい変数を無視すると \(\Phi_{2}\) を充足させる入力となる。
例えば例として出した回路は次の 3CNF 式となります: \[ \begin{aligned} & (y_1 ∨ x_1 ∨ x_4) ∧ (y_1 ∨ x_1 ∨ z_1) ∧ (y_1 ∨ x_1 ∨ z_1) ∧ (y_1 ∨ x_4 ∨ z_2) ∧ {} \\ & (y_1 ∨ x_4 ∨ z_2) ∧ (y_2 ∨ x_4 ∨ z_3) ∧ (y_2 ∨ x_4 ∨ z_3) ∧ (y_2 ∨ x_4 ∨ z_4) ∧ {} \\ & (y_2 ∨ x_4 ∨ z_4)∧ (y_3 ∨ x_3 ∨ y_2) ∧ (y_3 ∨ x_3 ∨ z_5) ∧ (y_3 ∨ x_3 ∨ z_5) ∧ {} \\ & (y_3 ∨ y_2 ∨ z_6) ∧ (y_3 ∨ y_2 ∨ z_6) ∧ (y_4 ∨ y_1 ∨ x_2) ∧ (y_4 ∨ x_2 ∨ z_7) ∧ {} \\ & (y_4 ∨ x_2 ∨ z_7) ∧ (y_4 ∨ y_1 ∨ z_8) ∧ (y_4 ∨ y_1 ∨ z_8) ∧ (y_5 ∨ x_2 ∨ z_9) ∧ {} \\ & (y_5 ∨ x_2 ∨ z_9) ∧ (y_5 ∨ x_2 ∨ z_{10}) ∧ (y_5 ∨ x_2 ∨ z_{10}) ∧ (y_6 ∨ x_5 ∨ z_{11}) ∧ {} \\ & (y_6 ∨ x_5 ∨ z_{11}) ∧ (y_6 ∨ x_5 ∨ z_{12}) ∧ (y_6 ∨ x_5 ∨ z_{12}) ∧ (y_7 ∨ y_3 ∨ y_5) ∧ {} \\ & (y_7 ∨ y_3 ∨ z_{13}) ∧ (y_7 ∨ y_3 ∨ z_{13}) ∧ (y_7 ∨ y_5 ∨ z_{14}) ∧ (y_7 ∨ y_5 ∨ z_{14}) ∧ {} \\ & (y_8 ∨ y_4 ∨ y_7) ∧ (y_8 ∨ y_4 ∨ z_{15}) ∧ (y_8 ∨ y_4 ∨ z_{15}) ∧ (y_8 ∨ y_7 ∨ z_{16}) ∧ {} \\ & (y_8 ∨ y_7 ∨ z_{16}) ∧ (y_9 ∨ y_8 ∨ y_6) ∧ (y_9 ∨ y_8 ∨ z_{17}) ∧ (y_9 ∨ y_6 ∨ z_{18}) ∧ {} \\ & (y_9 ∨ y_6 ∨ z_{18}) ∧ (y_9 ∨ y_8 ∨ z_{17}) ∧ (y_9 ∨ z_{19} ∨ z_{20}) ∧ (y_9 ∨ z_{19} ∨ z_{20}) ∧ {} \\ & (y_9 ∨ z_{19} ∨ z_{20}) ∧ (y_9 ∨ z_{19} ∨ z_{20}) \end{aligned} \]
この式は一見すると元の回路よりもはるかに複雑に見えますが、各ゲートが最大でも五つの節に変換されることから分かるように、実際には定数倍しか大きくありません。回路の大きさに対する式の大きさが (\(n^{374}\) のような) 次数の大きな多項式になったとしても、NP 困難性を示すための帰着としては何ら不都合はありません。
以上の帰着によって、任意のブール回路 \(K\) は多項式時間で 3CNF 式 \(\Phi_{3}\) に変換できます。また \(K\) を充足させる任意の入力は \(\Phi_{3}\) を充足させる入力に変換でき、その逆も行えます。言い換えれば「\(K\) が充足可能 \(\iff\) \(\Phi_{3}\) が充足可能」ということです。よってもし \(\textsc{3SAT}\) が多項式時間で解けるならば \(\textsc{CircuitSAT}\) も多項式時間で解くことができ、P=NP です。以上より、\(\textsc{3SAT}\) が NP 困難であると結論できます。
最大独立集合 (3SAT からの帰着)
これから考えるいくつかの問題において、入力は単純重み無し無向グラフ、出力は何らかの構造的な特徴を持つ部分グラフのうち最大または最小のものです。
\(G\) を任意のグラフとします。\(G\) の独立集合 (independent set) とは、\(G\) の頂点の集合でどの頂点の組の間にも辺が無いものを言います。最大独立集合問題、略して \(\textsc{MaxIndSet}\) は与えられたグラフに含まれる最大の独立集合の大きさを求める問題です。これから \(\textsc{MaxIndSet}\) が NP 困難であることを \(\textsc{3SAT}\) からの帰着を使って示します:
任意の 3CNF 式 \(\Phi\) が与えられたとき、次のようにしてグラフ \(G\) を構築します。\(\Phi\) に含まれる節の数を \(k\) とすると \(G\) には \(3k\) 個の頂点があり、それぞれが \(\Phi\) のリテラルに対応します。\(G\) の任意の二つの頂点の間に辺があるのは (1) 二つの頂点が同じ節にある、もしくは (2) 二つの頂点がある変数とその否定である、場合のみです。例えば \((a ∨ b ∨ c)\ ∧\) \((b ∨ \overline{c} ∨ \overline{d})\ ∧\) \( (\overline{a} ∨ c ∨ d)\ ∧\) \((a ∨ \overline{b} ∨ \overline{d})\) という式は次のグラフに変形されます:
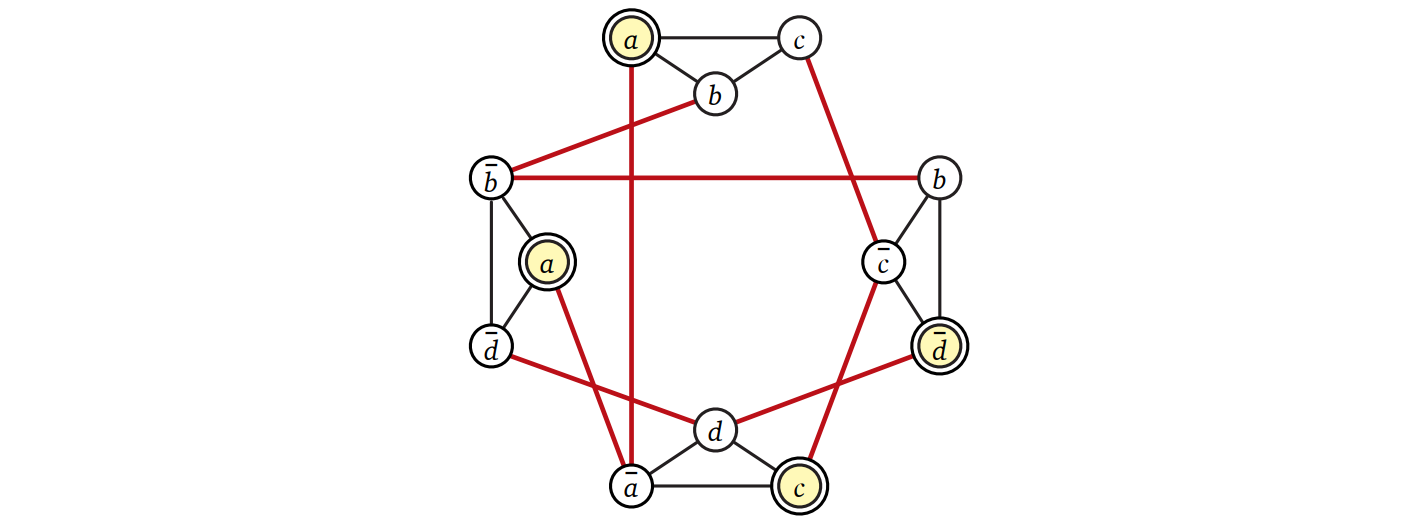
\(\Phi\) の節に含まれる三つのリテラルに対応する \(G\) の頂点は全て辺で結ばれて三角形を作るので、\(G\) の独立集合はグラフの各三角形につき最大でも一つしか頂点を含みません。よって \(G\) の最大独立集合の大きさは最大でも \(k\) です。これから 「\(G\) に大きさ \(k\) の独立集合が存在する」と「元の式 \(\Phi\) が充足可能である」が同値であることを示します。 "同値である" ことの証明の常として、証明は二つの部分からなります。
-
\((\Rightarrow)\) \(\Phi\) が充足可能だと仮定する。\(\Phi\) を充足させる適当な真偽値割り当てを取ると、\(\Phi\) の全ての節には少なくとも一つの \(\textsc{True}\) のリテラルが含まれる。よってそのようなリテラルを集めることで、大きさが \(k\) の \(G\) の頂点の部分集合であって頂点全てが異なる三角形に含まれるものが作ることができる。この集合を \(S\) とすると、\(S\) の各頂点は異なる三角形に含まれることから、\(S\) の任意の頂点の組の間には三角形の辺がない。また \(S\) に含まれる頂点は全て \(\textsc{True}\) のリテラルに対応するから、\(S\) の任意の頂点の組の間にはあるリテラルとその否定を結ぶ辺もない。したがって \(S\) は大きさ \(k\) の \(G\) の独立集合である。
-
\((\Leftarrow)\) \(G\) が大きさ \(k\) の独立集合 \(S\) を持つとする。\(G\) の三角形は辺で結ばれていることから、\(S\) の各頂点は異なる三角形に含まれていなければならない。あるリテラルとその否定の間には辺が存在することから、\(S\) に含まれるリテラル全てに \(\textsc{True}\) を割り当てるような真偽値割り当てを考えることができる。ただし \(x\) と \(\overline{x}\) がどちらも \(S\) に含まれないようなリテラルがあった場合には、適当な値を割り振ることにする。こうして出来上がる真偽値割り当てでは \(\Phi\) の全ての節に少なくとも一つの \(\textsc{True}\) リテラルが含まれるので、\(\Phi\) は充足可能だと分かる。
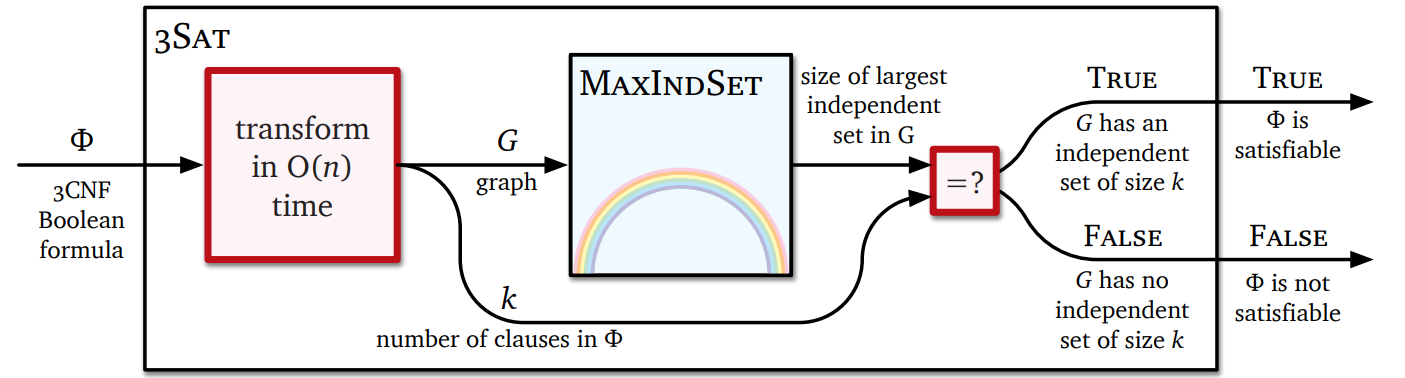
3CNF 式 \(\Phi\) のグラフ \(G\) への変換は、総当たりを使ったとしても多項式時間で行えます。よって \(\textsc{3SAT}\) の入力 \(\Phi\) をグラフ \(G\) に変換した上で \(G\) に含まれる最大独立集合の大きさと \(\Phi\) に含まれる節の数を比べるという方法を使えば、\(\textsc{MaxIndSet}\) を多項式時間で解けるときに \(\textsc{3SAT}\) を多項式時間で解くことができます。もしそうならば P=NP なので、何かがおかしいです! よって \(\textsc{MaxIndSet}\) は NP 困難だと結論できます。
共通するパターン
NP 困難性の証明、そして一般的には全ての多項式時間帰着には、共通するパターンがあります。問題 \(X\) から問題 \(Y\) への多項式時間帰着には次のステップが必要です:
-
\(X\) の任意のインスタンス \(x\) を \(Y\) の特殊なインスタンス \(y\) に変換する多項式時間アルゴリズムを示す。
-
\(x\) が \(X\) の "良い" インスタンスならば \(y\) は \(Y\) の "良い" インスタンスであると示す。
-
\(y\) が \(Y\) の "良い" インスタンスならば \(x\) は \(X\) の "良い" インスタンスであると示す (通常最も難しくなるのはこの部分)。
もちろん正しい帰着を開発するときにはこれらの作業を一つずつ処理するのではありません。上手く行くと思われるアルゴリズムを書くところから初めてその後に正しさを証明するというやり方はまず上手く行かず、試験のように時間が限られているような状況では特にそうです。アルゴリズムの開発、"if" の証明、"only if" の証明は同時に行わなければなりません。
晩年の Ricky Jay の言葉を借りるなら9、「これは後天的に身に着けるスキルです」
多くの生徒を困惑させるのは、帰着アルゴリズムが "片方向にしか"、つまり \(X\) から \(Y\) にしか帰着を行わないにもかかわらず、正しさの証明は "両方向に" 必要となる点です。しかしよく考えてみれば、証明は対称的ではありません。"if" の証明は任意のインスタンス \(x\) を扱うのに対して、"only if" の証明は帰着アルゴリズムによって生成される \(Y\) の特殊なインスタンスだけを扱うからです。この非対称性をうまく利用することが正しい帰着を設計するための鍵です。
あるインスタンスが "良い" ことの証明を「証拠 (certificate)」と呼ぶようにすると分かりやすいでしょう。例えば \(\textsc{CircuitSAT}\) のインスタンスに対する証拠は電球を灯らせるような入力であり、\(\textsc{SAT}\) や \(\textsc{3SAT}\) のインスタンスに対する証拠は式を充足させる真偽値割り当てです。この言葉を使うと、\(X\) から \(Y\) への帰着に必要なのは次の三つのアルゴリズムです:
-
\(X\) の任意のインスタンス \(x\) を \(Y\) の特殊なインスタンス \(y\) に多項式時間で変形する。
-
\(x\) に対する証拠を \(y\) に対する証拠に変換する。
-
\(y\) に対する証拠を \(x\) に対する証拠に変換する。
二番目と三番目のステップにおける \(x, y\) は一番目のアルゴリズムの入出力のことを指しています。証拠の変換は両方向に行える必要がありますが、インスタンスの変換はそうではありません。\(Y\) のインスタンスを変換する必要はなく、\(Y\) の任意のインスタンスについて考える必要もありません。また多項式時間で実行されなければならないのは最初のアルゴリズムだけです (ただし実際の証明ではまず間違いなく二番目と三番目のアルゴリズムが最初のアルゴリズムよりも単純になります)。
例えば \(\textsc{CircuitSAT}\) から \(\textsc{3SAT}\) への帰着は三つのアルゴリズムからなります:
-
任意のブール回路 \(K\) を特殊な 3CNF 式 \(\Phi_{3}\) に多項式時間で変換するアルゴリズム (全ての配線に新しい変数を割り当て、ゲートを同値な式に変換し、さらにその式を 3CNF に展開する)。
-
\(K\) を充足させる任意の入力を \(\Phi_{3}\) を充足させる真偽値割り当てに変換するアルゴリズム (入力を追跡して配線ごとの真偽値を計算し、対応する変数にその値を割り当てる。追加の変数には任意の値を割り当てる)。
-
\(\Phi_{3}\) を充足させる任意の真偽値割り当てを \(K\) を充足させる入力に変換するアルゴリズム (\(K\) の入力に対応する変数の値を取る)。
この帰着が上手く行くのは、任意の回路 \(K\) が高度に構造化された 3CNF 式 \(\Phi_{3}\) に変換されるためです。\(\Phi_{3}\) の構造によって、\(\Phi_{3}\) を充足させる真偽値割り当てが必ず \(K\) を充足させる入力から来るようになります。任意の 3CNF を考える必要はありません。
同様に、\(\textsc{3SAT}\) から \(\textsc{MaxIndSet}\) への帰着は三つのアルゴリズムからなります:
-
任意の 3CNF 式 \(\Phi\) を特殊なグラフ \(G\) と整数 \(k\) に多項式時間で変換するアルゴリズム。
-
\(\Phi\) を充足させる任意の真偽値割り当てを \(G\) に含まれる大きさ \(k\) の独立集合に変換するアルゴリズム。
-
\(G\) に含まれる任意の大きさ \(k\) の独立集合を \(\Phi\) を充足させる真偽値割り当てに変換するアルゴリズム。
ここでも最初の変換によって \(\Phi\) が高度に構造化されたグラフ \(G\) と整数 \(k\) に変換されます。このグラフ \(G\) の構造によって大きさ \(k\) の独立集合が必ず \(\Phi\) を充足させる真偽値割り当てから来るようになります。任意のグラフあるいは任意の大きさの独立集合を考える必要はありません。
クリークと頂点被覆 (最大独立集合からの帰着)
クリーク (clique) とはグラフに含まれる完全グラフ、つまり任意の頂点の組の間に辺がある部分グラフのことであり、\(\textsc{MaxClique}\) 問題とはグラフに含まれる最大のクリークの大きさを求める問題です。頂点被覆 (vertex cover) とはグラフの全ての辺に触れるような頂点の集合であり、\(\textsc{MinVertexCover}\) 問題とはグラフに含まれる最小の頂点被覆の大きさを求める問題です。
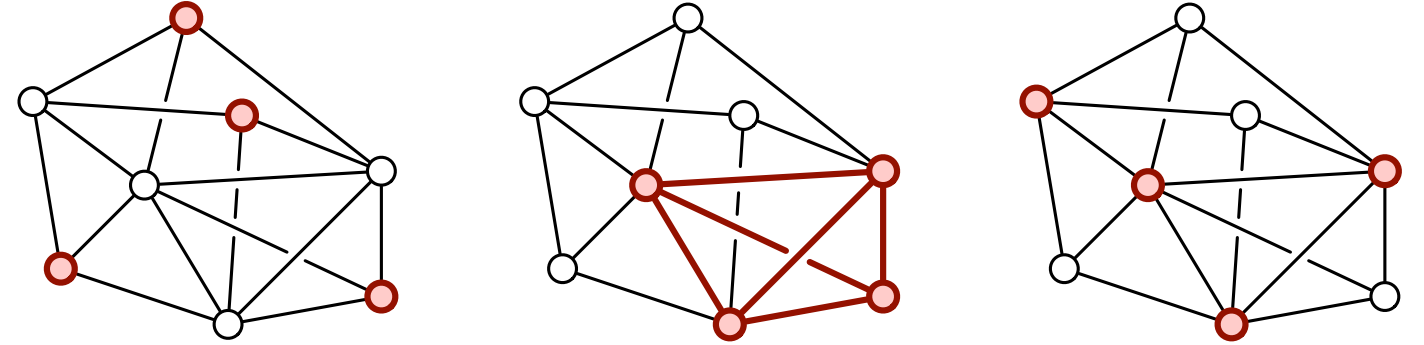
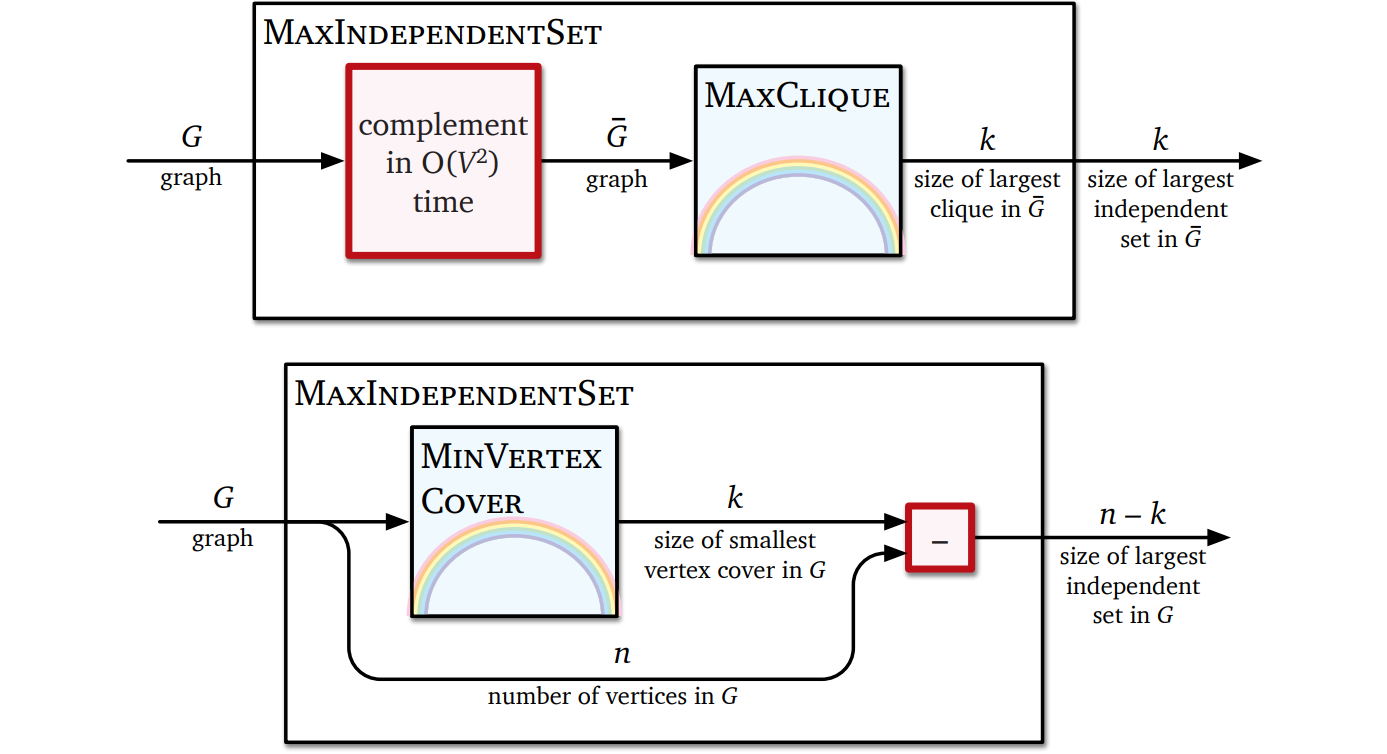
\(\textsc{MaxClique}\) が NP 困難であることは \(\textsc{MaxIndSet}\) からの簡単な帰着によって示せます。任意のグラフ \(G\) の辺の有無を反転させたものを辺補グラフ (edge-complement graph) \(\overline{G}\) と言います ―― \(\overline{G}\) の頂点は \(G\) と同じで、\(uv \in \overline{G}\) \(\iff\) \(uv \notin G\) です。\(G\) における最大独立集合は辺補グラフ \(\overline{G}\) における (同じサイズの) 最大クリークとなるので、帰着は簡単に作れます。
\(\textsc{MinVertexCover}\) が NP 困難であることの証明はさらに簡単です: グラフ \(G=(V,E)\) の独立集合を \(I\) とすると、その補集合 \(V \backslash I\) は同じグラフ \(G\) の頂点被覆となります。よってグラフの最大独立集合は同じグラフの最小頂点被覆の補集合です! \(n\) 頂点のグラフの最小頂点被覆の大きさが \(k\) ならば、最大独立集合の大きさは \(n-k\) となります。
グラフの彩色 (3SAT からの帰着)
グラフ \(G = (V,E)\) の真の \(\pmb{k}\)-彩色 (proper \(\pmb{k}\)-coloring) とは、各頂点に \(k\) 個ある色のどれかを割り当てる関数 \(C: V \rightarrow \lbrace 1, 2, \ldots, k \rbrace\) であって辺でつながれた任意の頂点に違う色が割り当てられるものを言います ("色" は適当なラベルであり、ここでは整数とします。電磁スペクトル、CMYK ベクトル、Pantone の色番号などは使いません)。グラフ彩色問題とは与えられたグラフを彩色するのに必要となる色の数の最小値を計算する問題です。
グラフ彩色問題が NP 困難であることを示すには、与えられたグラフは真の 3-彩色を持つかを判定する \(\textsc{3Color}\) 問題だけを考えれば十分です。これから \(\textsc{3Color}\) が NP 困難なことを \(\textsc{3SAT}\) からの帰着で示します (なぜ \(\textsc{3SAT}\) かというと、問題に \(3\) が含まれているからです。ふざけているのかと思うのかもしれませんが、私は真面目に言っています)。つまり 3CNF 式 \(\Phi\) が与えられたときに、\(\Phi\) が充足可能なときに限って 3-彩色可能となるグラフ \(G\) を作れば良いことになります:
ここでは出力のグラフ \(G\) をガジェット (gadget) ごとに作っていくという、帰着においてよく使われる戦略を使います。\(G\) の各ガジェットが、入力の式 \(\Phi\) が持つ様々な特徴を表します。帰着をガジェットに分解して考えることは既存の帰着を理解するのに有用なだけでなく、NP 困難性を証明するための新しい帰着を考えるときにも有用です10。
今考えている論理式からグラフへの帰着は三つのガジェットからなります:
-
真偽値ガジェット: 三角形をなす頂点 \(T\), \(F\), \(X\) があり、それぞれが \(\textsc{True}\), \(\textsc{False}\), \(\textsc{Other}\) に対応する。この三つの頂点は全て辺でつながっており、3-彩色において異なる色が塗られる。議論を簡単にするために、以降これらの色を \(\textsc{True}\), \(\textsc{False}\), \(\textsc{Other}\) と呼ぶ。例えばある頂点が \(\textsc{True}\) に塗られていると言ったときには、その頂点が \(T\) と同じ色で塗られていることを意味する。
-
変数ガジェット: \(\Phi\) の任意の変数 \(a\) に対して、\(a\) とラベルの付いた頂点、\(\overline{a}\) とラベルの付いた頂点、真偽値ガジェットの頂点 \(X\) からなる三角形がある。\(a\) は \(\textsc{True}\) または \(\textsc{False}\) に塗られ、それに対して \(\overline{a}\) は \(\textsc{False}\) または \(\textsc{True}\) に塗られる。
 図 12.9真偽値ガジェット (左) と変数 \(a\) に対応する変数ガジェット (右)
図 12.9真偽値ガジェット (左) と変数 \(a\) に対応する変数ガジェット (右) -
節ガジェット: \(\Phi\) の各節に対して、三つのリテラルに対応する (変数ガジェットの) 頂点と (真偽値ガジェットの) 頂点 \(T\) を、ラベルの無い頂点を五つ使って次のようにつなぐ:
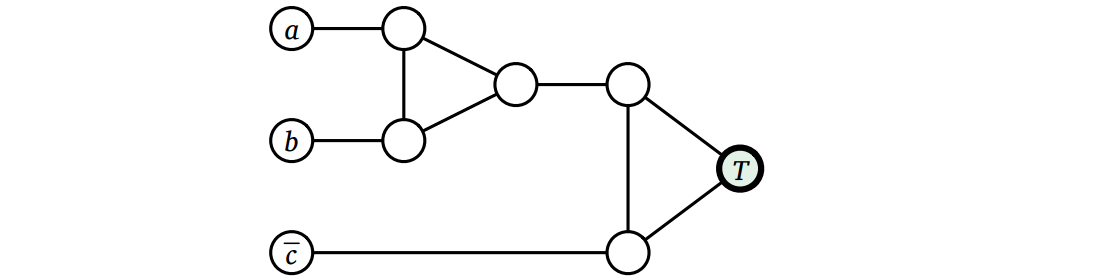 図 12.10\((a \lor b \lor \overline{c})\) に対応する節ガジェット
図 12.10\((a \lor b \lor \overline{c})\) に対応する節ガジェットこうしたとき、二つの三角形は "マジョリティゲート" のように機能する。つまり任意の真の 3-彩色において、もし左の二つの頂点が同じ色だった場合には右の頂点はその色と同じになり、そうでなく左の二つの頂点が違う色であった場合には右の頂点は任意の色になれる (下図参照)。
よって節ガジェットに含まれる三つのリテラルが全て \(\textsc{False}\) になることはないと分かる。逆に節ガジェットに含まれる三つのリテラルに対する二つ以上の色を使った任意の彩色が与えられば、その彩色を節ガジェット全体の彩色に拡張できる。変数ガジェットの構成からリテラルの頂点には \(\textsc{True}\) または \(\textsc{False}\) のどちらかが塗られることが言えるので、節ガジェットの任意の彩色は少なくとも一つのリテラルの頂点に \(\textsc{True}\) を塗る。
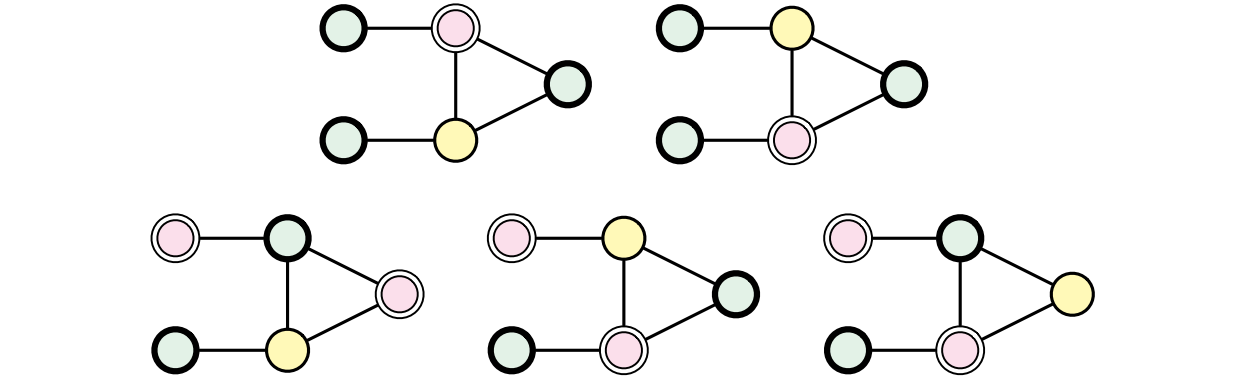 図 12.11「半分の」ガジェットに対する全ての真 3-彩色 (色の置換を同一視している)
図 12.11「半分の」ガジェットに対する全ての真 3-彩色 (色の置換を同一視している)
最終的に出来上がるグラフ \(G\) には、頂点 \(T\), \(F\), \(X\) そして各変数 \(a\) に対応する頂点 \(a\) および \(\overline{a}\) がちょうど一つずつ含まれます。例えば \((a ∨ b ∨ c)\ ∧\) \((b ∨ \overline{c}\ ∨\) \(\overline{d})\ ∧\) \((\overline{a} ∨ c ∨ d)\ ∧\) \((a ∨ \overline{b} ∨ \overline{d})\) という、以前に \(\textsc{MaxClique}\) を説明するときに使った論理式は次のグラフになります。図中の 3-彩色は式を充足させる真偽値割り当ての一つ \(a = b = \textsc{True}\), \(b = d = \textsc{False}\) に対応します。
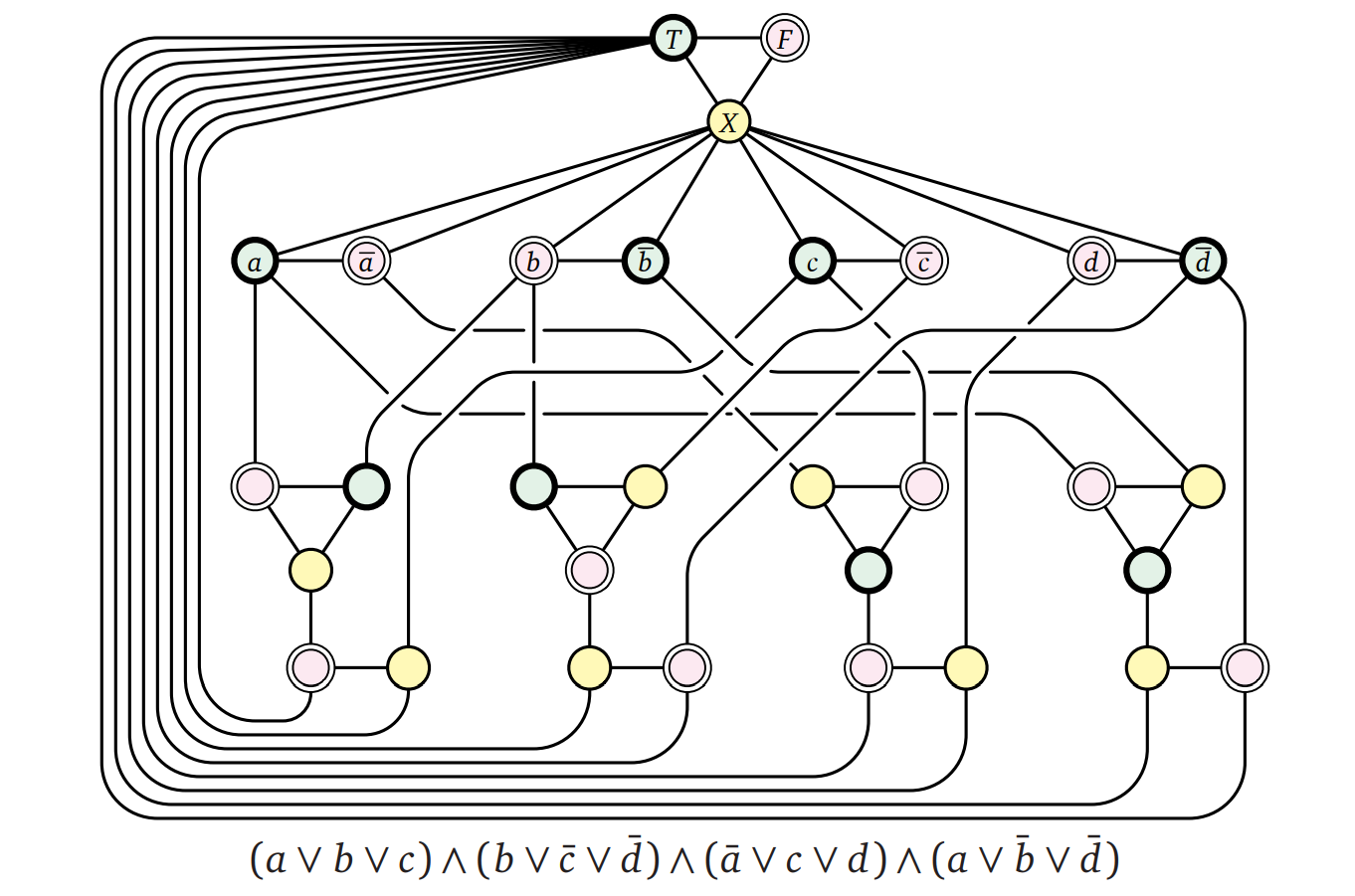
こうして出来上がるグラフの正しさの証明はこれまでにほぼ終わっています。式が充足可能ならば、任意の真偽値割り当てに基づいてリテラルの頂点を彩色でき、さらに (どの節にも \(\textsc{True}\) と \(\textsc{False}\) が少なくとも一つ含まれることから) その彩色を全ての節ガジェットに対する彩色に拡張できます。逆にグラフが 3-彩色可能ならば彩色から変数に対する真偽値割り当てを作ることができ、その割り当ては各節の少なくとも一つのリテラルを \(\textsc{True}\) にするので、全体の式を充足させます。
したがって \(\textsc{3Color}\) は NP 困難です。\(\textsc{3Color}\) は一般的な彩色問題 (「彩色に必要な色は最低何色?」) の特殊ケースなので、この一般的な最適化問題も NP 困難です。
ハミルトン閉路
ハミルトン閉路 (Hamiltonian cycle) とはグラフの全ての頂点をちょうど一回ずつ訪れる閉路のことです (オイラー閉路 (Eulerian cycle) とは異なります。オイラー閉路は全ての辺をちょうど一回ずつ使う閉じた歩道であり、深さ優先探索を使って線形時間で簡単に見つけられます)。ここでは有向グラフに対するハミルトン閉路問題が NP 困難であることの証明を二つ示します。
頂点被覆からの帰着
ハミルトン閉路問題の NP 困難性の証明の一つ目は、判定バージョンの頂点被覆問題からの帰着を使うものです。この証明では与えられた無向グラフ \(G\) と整数 \(k\) から、有向グラフ \(H\) であって \(H\) にハミルトン閉路が存在するときに限って \(G\) に大きさ \(k\) の頂点被覆が存在するようなものを構成します。一つ前の帰着と同じように、出力のグラフ \(H\) はいくつかのガジェットからなり、それぞれのガジェットが入力のグラフ \(G\) と整数 \(k\) の特徴を反映します。
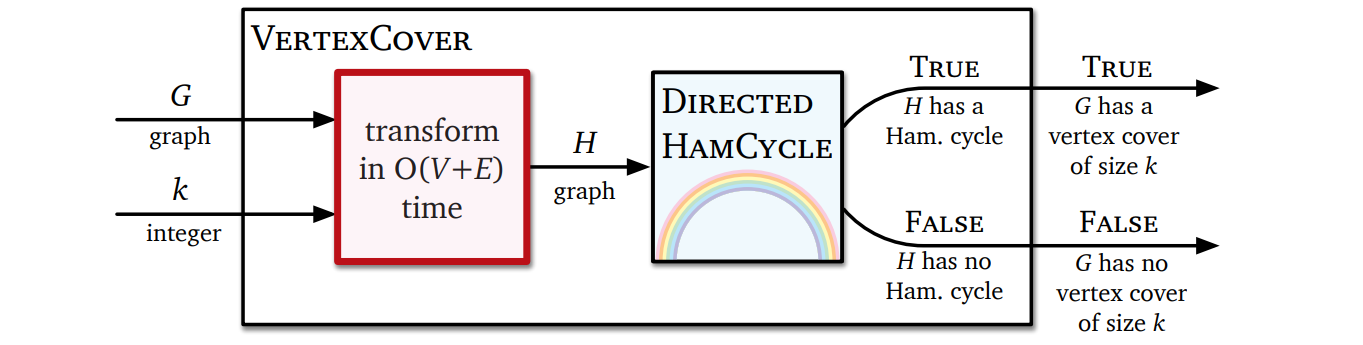
-
\(G\) の全ての無向辺 \(uv\) に対して、\(H\) は辺ガジェットとして頂点 \((u,v,\text{in})\), \((u,v,\text{out}) \), \((v,u,\text{in})\), \((v,u,\text{out}) \) およびその間の辺 \[ \begin{aligned} (u, v,\text{in}) & \rightarrow (u, v, \text{out})& (u, v,\text{in}) & \rightarrow (v, u,\text{in}) \\ (v, u,\text{in}) & \rightarrow (u, v,\text{in})& (v, u,\text{in}) & \rightarrow (v, u, \text{out}) \\ (u, v, \text{out}) & \rightarrow (v, u, \text{out})& (v, u, \text{out}) & \rightarrow (u, v, \text{out}) \end{aligned} \] を持つ。下図にあるように、これらの辺以外に "in" 頂点には入ってくる辺が、"out" 頂点には出ていく辺がある。ここで \(H\) の任意のハミルトン閉路について、辺ガジェットの通り抜け方は三種類しかない。つまり、両方の道を別々に通るか、右の道から入って全ての頂点をたどるか、左の道から入って全ての頂点をたどるかである。
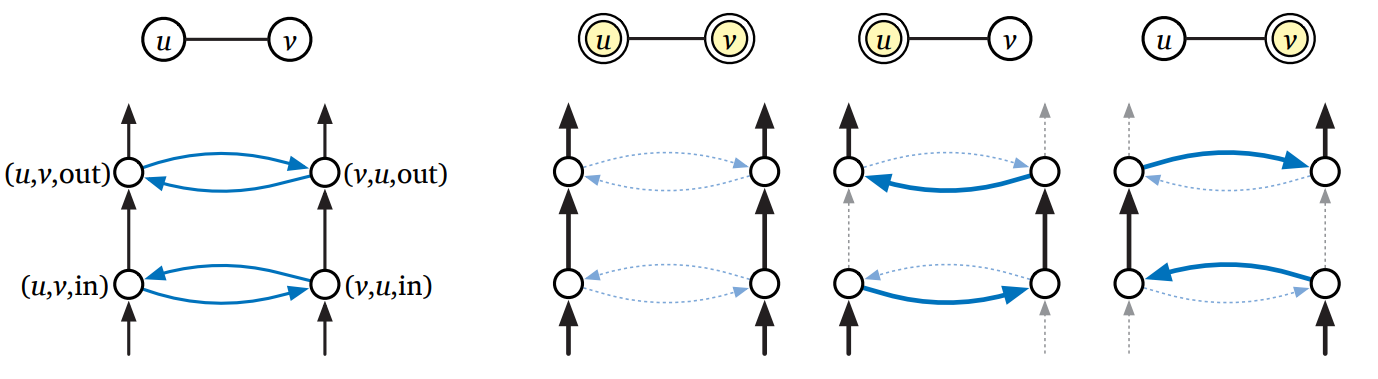 図 12.13辺ガジェットとそれを通り抜けるハミルトン閉路 (の一部)
図 12.13辺ガジェットとそれを通り抜けるハミルトン閉路 (の一部) -
\(G\) の任意の頂点 \(u\) について、\(u\) に隣接する辺 \(uv\) の辺ガジェットは \(H\) において一つの有向路でつながれている。この辺ガジェットが連なったものを頂点鎖 (vertex chain) と呼ぶ。具体的に言うと、\(u\) に隣接する頂点を \(v_{1}, v_{2}, \ldots, v_{d}\) としたとき、 \(H\) には \(i = 1 \ldots d-1\) に対して \((u, v_{i}, \text{out})\) \(\rightarrow\) \((u, v_{i+1}, \text{in})\) という辺がある。
-
\(H\) には \(k\) 個の被覆頂点 (cover vertex) \(x_{1}, x_{2}, \ldots, x_{k}\) があり、各 \(x_{i}\) には各頂点鎖の最初の頂点への辺、および各頂点鎖の最後の頂点からの辺がある。
この帰着の完全な例を次の図に示します。
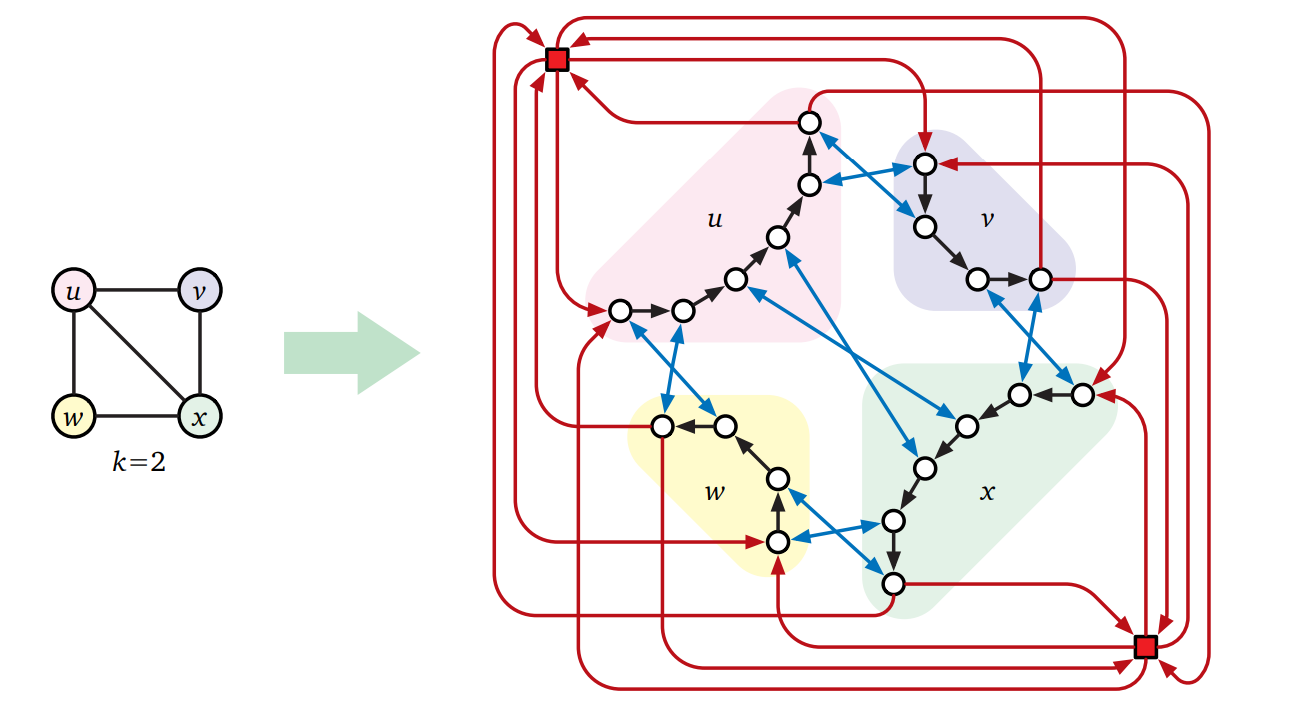
「\(G\) に大きさ \(k\) の頂点被覆がある \(\iff\) \(H\) にハミルトン閉路がある」の証明はいつも通り二つのステップからなります。
-
\((\Rightarrow)\) \(C = \lbrace u_{1}, u_{2}, \ldots, u_{k} \rbrace\) が \(G\) の頂点被覆であると仮定する。このとき次のようにして \(H\) の閉路を構築する。閉路は \(x_{1}\) から始まり、任意の添え字 \(i = 1, \ldots, k\) について \(x_{i}\) から \(u_{i}\) の頂点鎖を通って \(x_{i+1}\) に至る。\(u_{i}\) の頂点鎖を通り抜けるとき、各頂点 \((u_{i}, v, \text{in})\) の次の頂点は次のように定める:
-
\(v \in C\) ならば \((u_{i}, v, \text{in}) \rightarrow (u_{i}, v, \text{out})\) と頂点鎖を素直にたどる。
-
\(v \notin C\) ならば \((u_{i}, v, \text{in}) \rightarrow\) \((v, u_{i}, \text{in}) \rightarrow\) \((v, u_{i}, \text{out}) \rightarrow\) \((u_{i}, v, \text{out})\) と迂回して頂点鎖をたどる。
\(G\) の各辺 \(uv\) について、こうして出来上がる閉路が \((u,v,\text{in})\) と \((u,v,\text{out})\) を訪れるのは、\(u \in C\) ならば \(u\) の頂点鎖をたどるときであり、\(u \notin C\) ならば \(v\) の頂点鎖をたどるときである。次の図も参照:
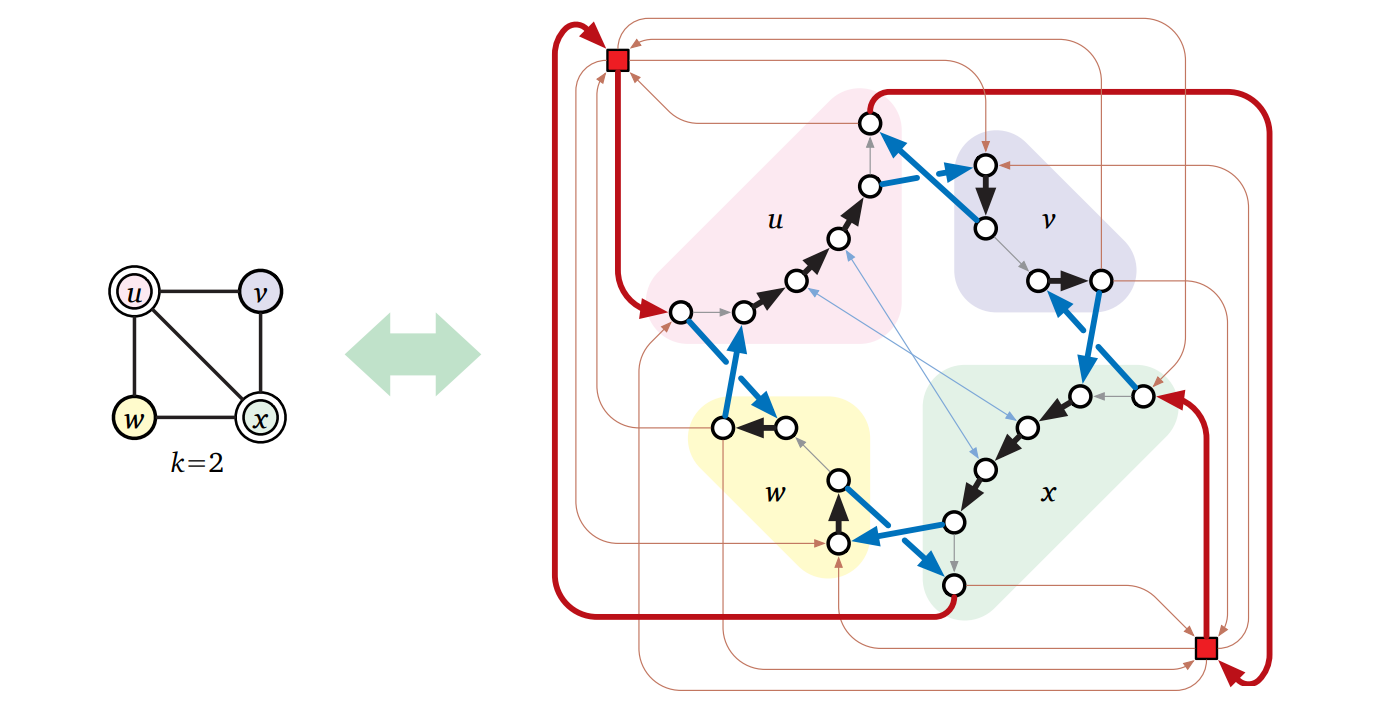 図 12.15\(G\) の大きさ \(k\) の任意の頂点被覆は \(H\) のハミルトン閉路に対応し、その逆も成立する
図 12.15\(G\) の大きさ \(k\) の任意の頂点被覆は \(H\) のハミルトン閉路に対応し、その逆も成立する\(C\) が頂点被覆なことから、こうして出来上がる閉路は \(H\) の辺ガジェットに含まれる頂点を全て訪れる。\(H\) の被覆頂点以外の頂点は全ていずれかの辺ガジェットに含まれるから、この閉路はハミルトン閉路である。
-
-
\((\Leftarrow)\) \(H\) にハミルトン閉路 \(C\) が含まれるとする。\(C\) には被覆頂点から頂点鎖の最初の頂点への辺が少なくとも一つ含まれる。ハミルトン閉路が辺ガジェットをどう通り抜けるかについての考察から、\(C\) が頂点鎖に入ったときにはその頂点鎖から出てくることが帰納的に分かる。よって \((u,v,\text{in})\) という形の任意の頂点について、\(C\) には \((u,v,\text{in}) \rightarrow (u, v, \text{out})\) という単一の辺または \((u, v, \text{in}) \rightarrow\) \((v, u, \text{in}) \rightarrow\) \((v, u, \text{out}) \rightarrow\) \((u, v, \text{out})\) という迂回路が含まれる。この辺または迂回路の後にあるのは \(u\) が頂点鎖の最後の頂点である場合には被覆頂点であり、そうでない場合は \(u\) の頂点鎖における次の辺ガジェットである。
ハミルトン閉路が辺ガジェットをどう通り抜けるかについての考察から、\(C\) に迂回路 \((u, v, \text{in}) \rightarrow\) \((v, u, \text{in})\) が含まれるときには、\(v\) の頂点鎖の端点と被覆頂点を結ぶ辺は \(C\) に含まれないことが言える。よって \(C\) が最初の頂点から入って最後の頂点から出る頂点鎖の数はちょうど \(k\) 個である。\(G\) の各辺 \(uv\) について \(C\) は \((u, v, \text{in})\) の形の頂点を全て訪れるので、\(C\) が最初から最後まで通り抜ける頂点鎖に対応する頂点の集合は大きさ \(k\) の頂点被覆となる。
以上より、「\(G\) に大きさ \(k\) の頂点被覆がある \(\iff\) \(H\) にハミルトン閉路がある」が言えます。\(G\) から \(H\) への変換には最大でも \(O(n^{2})\) 時間しかかからないので、有向グラフに対するハミルトン閉路問題が NP 困難であることが分かります。
3SAT からの帰着
ハミルトン閉路問題の NP 困難性は 3SAT からの帰着を使っても示すことができます。与えられた 3CNF 式 \(\Phi\) が \(n\) 個の変数 \(x_{1}, x_{2}, \ldots, x_{n}\) と \(k\) 個の節 \(c_{1}, c_{2}, \ldots, c_{k}\) を持つとし、\(\Phi\) が充足可能なときに限ってハミルトン閉路を持つような有向グラフ \(H\) をこれから構築します。
\(H\) には \(\Phi\) の各変数に対応する変数ガジェットが含まれます。変数 \(x_{i}\) に対する変数ガジェットは \(2k\) 個の頂点 \((i,0), (i,1), \ldots, (i,2k)\) を持ち、任意の添え字 \(j\) について \((i, j-1) \rightarrow (i,j)\) および \((i, j) \rightarrow (i, j-1)\) という辺を持ちます。
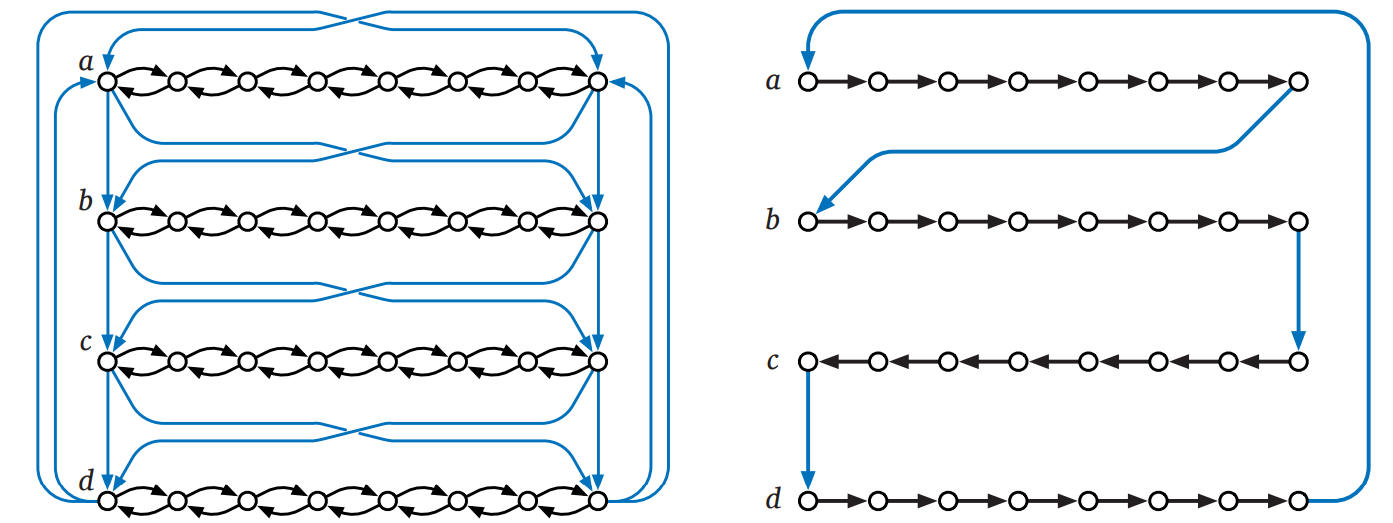
さらに隣り合う変数ガジェットの最初と最後の頂点は辺で結ばれます。つまり任意の添え字 \(i\) について \[ \begin{aligned} (i, 0) & \rightarrow (i+1, 0) & (i, 2k) & \rightarrow (i+1, 0) \\ (i, 0) & \rightarrow (i+1, 2k) & (i, 2k) & \rightarrow (i+1, 2k) \end{aligned} \] という辺が存在します。加えて最初と最後の変数ガジェットは次の辺で結ばれます: \[ \begin{aligned} (n, 0) & \rightarrow (1, 0) & (n, 2k) & \rightarrow (1, 0) \\ (n, 0) & \rightarrow (1, 2k) & (n, 2k) & \rightarrow (1, 2k) \end{aligned} \]
こうして出来上がるグラフ \(G\) にはちょうど \(2^{n}\) 個のハミルトン路が含まれ、それぞれが \(\Phi\) の \(n\) 個の変数に対する異なる真偽値割り当てに対応します。具体的には、\(i\) 番目のガジェットを左から右にたどるなら \(x_{i} = \textsc{True}\) であり、右から左なら \(x_{i} = \textsc{False}\) です。次の図も参照してください:
\(\Phi\) の各節 \(c_{j}\) に対応する節ガジェットを \(G\) に加えることで \(H\) を作ります。節 \(c_{j}\) に対応する節ガジェットには一つの頂点 \([j]\) が含まれ、\([j]\) と変数ガジェットの間には次の図に示すような 6 本の辺が存在します。つまり、\(c_{j}\) の正のリテラル \(x_{i}\) に対しては辺 \((i, 2j - 1) \rightarrow\) \([j] \rightarrow\) \((i, 2j)\)、\(c_{j}\) の負のリテラル \(\overline{x}_{j}\) に対しては \((i,2j) \rightarrow\) \([j] \rightarrow\) \((i, 2j - 1)\) です。
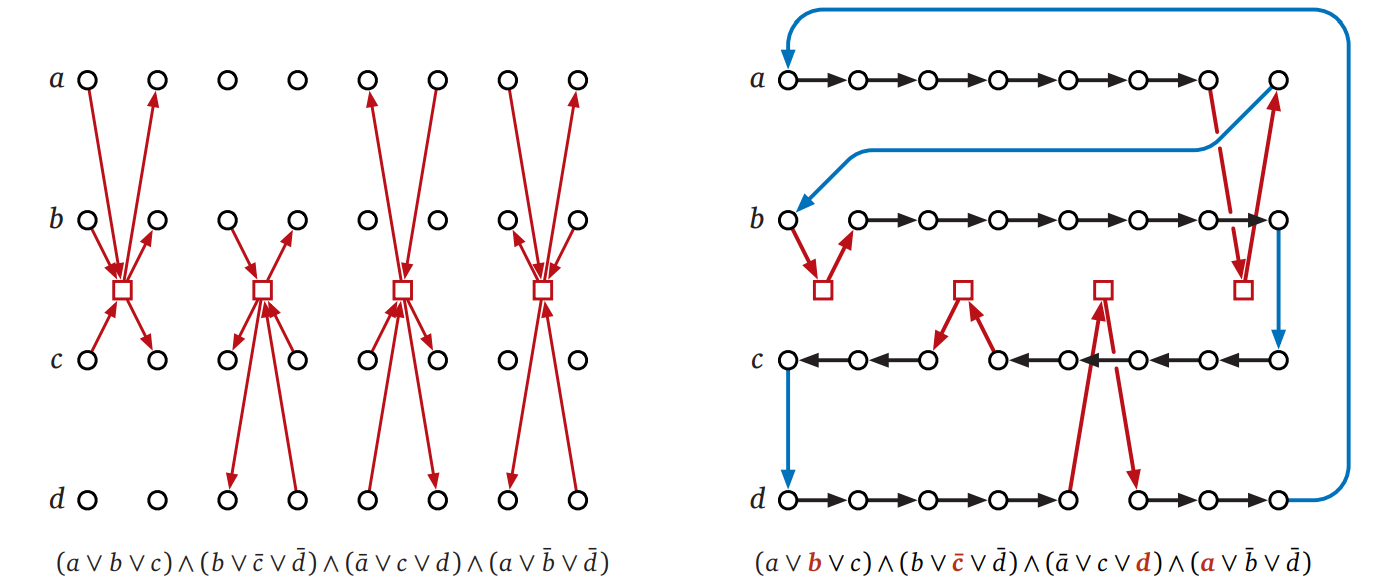
節ガジェットの辺の構成から、\(G\) のハミルトン閉路が \(H\) のハミルトン閉路に拡張できるのは対応する真偽値割り当てが \(\Phi\) を充足させるときに限られることが言えます。しらみつぶしに場合分けをしていけば、「\(H\) がハミルトン閉路を持つ \(\iff\) \(\Phi\) が充足可能」が示せます。
論理式 \(\Phi\) を \(H\) に変換するには \(O(kn)\) の時間かかりますが、これは最大でも \(\Phi\) の全長の二次式です。よって有向グラフに対するハミルトン閉路問題が NP 困難であると結論できます。
変種と拡張
前述の帰着を少し変更すると、ハミルトン "路" 問題が NP 困難であることも示せます。ここで \(G\) のハミルトン路とはもちろん \(G\) の全ての頂点をちょうど一回ずつ通る単純路のことです。実は \(\textsc{HamiltonianCycle}\) と \(\textsc{HamiltonianPath}\) の間には多項式時間帰着が双方向に存在します。どちらの帰着も簡単なので、詳細は練習問題とします。
この節で説明した二つの帰着はどちらも有向グラフを扱っていますが、無向グラフに対するハミルトン閉路問題も NP 困難です。実は有向グラフに対するハミルトン閉路問題から無向グラフに対するハミルトン閉路問題への簡単な帰着が存在します。この帰着の詳細も楽しい練習問題とします。
最後に、悪名高き巡回セールスマン問題 (traveling salesman problem) は辺に重みの付いたグラフにおける最短のハミルトン閉路 (または路) を見つける問題と言えます。最短の閉路/路を見つけるのは閉路/路が存在するかを判定するよりも明らかに難しい ――辺の重みが全て \(1\) のグラフを考えてみてください!―― ので、巡回セールスマン問題も同じく NP 困難です。
部分和 (最小頂点被覆からの帰着)
次に NP 困難性を示す問題は二章で登場した \(\textsc{SubsetSum}\) です。この問題では正の整数の集合 \(X\) と整数 \(T\) が与えられ、\(X\) の部分集合で要素の和が \(T\) となるものが存在するかどうかを判定します。
ここでも \(\textsc{VertexCover}\) からの帰着を作ります。つまり任意の無向グラフ \(G\) と整数 \(k\) から整数の集合 \(X\) と整数 \(T\) を構築し、\(G\) に大きさ \(k\) の頂点被覆が存在するときに限って和が \(T\) の \(X\) の部分集合があるようにするということです。ここで説明する帰着には二種類のガジェットがあり、それぞれ \(G\) の頂点と辺に対応します。
\(G\) の辺に適当な順番で \(0\) から \(m-1\) の番号を振ります。こうしたとき \(X\) の要素は各辺 \(i\) に対する \(b_{i} := 4^{i}\) という整数と、各頂点 \(v\) に対する \[ a_{v} := 4^{m} + \sum_{i \in \Delta(v)} 4^{i} \] という整数です。ここで \(\Delta (v)\) は \(v\) を端点に持つ辺の集合を表します。
\(X\) の要素が \(m+1\) 桁の四進数で表されていると思うこともできます。つまり \(X\) に含まれる整数が表すのは \(m\) 桁目が \(1\) ならば頂点、\(0\) なら辺であり、\(i < m\) について \(i\) 桁目の \(1\) が辺 \(i\) または辺 \(i\) の端点を表します。
そしてターゲットとなる整数 \(T\) は次のように定めます: \[ T := k \cdot 4^{m} + \sum_{i=0}^{m-1} 2 \cdot 4^{i} \] それでは、この帰着が正しいことを示しましょう。
-
\((\Rightarrow)\) \(G\) に大きさ \(k\) の頂点被覆があると仮定する。\(X_{C} \subseteq X\) を
-
大きさ \(k\) の頂点被覆に含まれる頂点 \(v\) に対する \(a_{v}\) を全て含み、
-
大きさ \(k\) の頂点被覆に含まれる頂点を端点のちょうど一方に持つ辺 \(i\) に対する \(b_{i}\) を全て含む
ものとして定義する。このとき \(X_{C}\) に含まれる整数の和を四進法で書くと、最初の \(m\) 桁には全て \(2\) が並び、\(m\) 桁より上位の桁は \(k\) となる。つまり、\(X_{C}\) の和は \(T\) に等しい。
-
-
\((\Leftarrow)\) \(X^{\prime} \subseteq X\) の和が \(T\) になると仮定する。このとき \[ \sum_{v \in V^{\prime}} a_{v} + \sum_{i \in E^{\prime}} b_{i} = T \] となる \(V^{\prime} \subseteq V\) と \(E^{\prime} \subseteq E\) を取ることができる。
ここでも \(T\) を四進数で表したとする。\(X\) には \(i < m\) 桁が \(1\) の整数が三つしかないので、\(T\) を計算するときには最初の \(m\) 桁で繰り上がりは起きない。また各辺 \(b_{i}\) は \(i\) 桁目に \(1\) を持ち、\(T\) の \(i\) 桁目は \(2\) なことから、\(V^{\prime}\) には \(G\) の各辺の少なくとも一方の端点が含まれる。つまり、\(V^{\prime}\) は頂点被覆である。
また \(4^{m}\) より大きいのは頂点に対応する整数だけであり、\(\lfloor T / 4^{m} \rfloor = k\) であることから、\(V^{\prime}\) の大きさは \(k\) 以下である (実際にはちょうど \(k\) であり、証明は難しくない)。
例えばグラフ \(G = (V,E)\) において \(V = \lbrace u,\) \(v,\) \(w,\) \(x \rbrace\) および \(E = \lbrace uv,\) \(uw,\) \(vw,\) \(vx,\) \(wx \rbrace\) だった場合、\(X\) の一例は次の通りです: \[ \begin{aligned} a_u & := 111000_4 = 1344 & b_{uv} & := 010000_4 = 256 \\ a_v & := 110110_4 = 1300 & b_{uw} & := 001000_4 = 64 \\ a_w & := 101101_4 = 1105 & b_{vw} & := 000100_4 = 16 \\ a_x & := 100011_4 = 1029 & b_{vx} & := 000010_4 = 4 \\ & & b_{wx} & := 000001_4 = 1 \end{aligned} \] 大きさ \(2\) の頂点被覆を探している場合には、ターゲットとなる整数は \(T = 222222_{4} \) \(= 2730\) となります。頂点被覆 \(\lbrace v,w \rbrace\) は \(\lbrace a_{v},\) \( a_{w},\) \( b_{uv},\) \( b_{uw},\) \( b_{vx},\) \(b_{wx} \rbrace\) という \(X\) の部分集合に対応し、その和は確かに \(1300+1105+\) \(256+64+4+1 =\) \(2730\) となります。
この帰着は明らかに多項式時間で実行できます。\(\textsc{VertexCover}\) が NP 困難であることは前に示したので、\(\textsc{SubsetSum}\) が NP 困難であることが分かります。
読者への注意!
ここで強調しておくべきことがあります。300 ページほど前、三章で示したアルゴリズムは \(\textsc{SubsetSum}\) を \(O(nT)\) 時間で解きます。これは多項式時間アルゴリズムなのでは? つまり、ちょうど今 P=NP を証明したのでは? あれ、私の百万ドルはどこ?
残念ながら、人生はそう簡単にはいきません。もちろん、このアルゴリズムの実行時間は \(n\) と \(T\) の多項式で抑えられています。しかし多項式時間アルゴリズムとなるためには、実行時間が入力を表現するのに必要となるビット数の多項式である必要があります。\(X\) の要素の値と \(T\) の値は入力ビット数に対して指数的に大きくなることができ、そもそもここで示した帰着では \(T\) の値が入力グラフの大きさに対して指数的に大きくなっています。このような入力 \(T\) に対して動的計画法のアルゴリズムを適用すると実行時間が指数的になるので、動的計画法のアルゴリズムは多項式時間アルゴリズムとは言えません。
このような特徴を持つアルゴリズムは擬多項式時間 (pseudo-polynomial time) で実行できると言い、そのような NP 困難問題は弱 NP 困難 (weakly NP-hard) であると言います。つまり弱 NP 困難な問題とは、入力が一進数 (表す数の個数だけ \(1\) を並べたもの) で表されると多項式時間で解けるものの、入力が二進数で表されると NP 困難となる問題です。
これに対して入力が一進数で表されたとしても NP 困難となる問題を、強 NP 困難 (strongly NP-hard) であると言います。例えば \(\textsc{TravelingSalesman}\) は強 NP 困難です。この問題は、入力を全ての辺の重みが \(1\) または \(2\) である完全グラフに限った場合でも NP 困難となります。
その他の便利な NP 困難問題
文字通り数千もの問題が NP 困難であると示されています。ここでは帰着を導くときに有用な NP 困難問題をいくつか紹介します。それぞれについて NP 困難性の証明の詳細を述べることはしませんが、ほとんどの問題に対する証明は Garey と Johnson による NP 完全性についての恐ろしい黒本11に載っています。ここまでに紹介した問題の全て、そしてこのリストにある問題のほとんどは、1972 年の Richard Karp (リチャード・カープ) による一つの画期的な論文で NP 困難であることが示されました12。
-
\(\textsc{PlanarCircuitSAT}\):「配線を交差させることなく平面に埋め込むことができるブール回路が与えられる。出力が \(\textsc{True}\) となるような入力が存在するか?」NP 困難性の証明は一般の回路充足問題からの帰着で行われる。帰着は一般の回路に含まれる交差するゲートをいくつかのゲートに置き換えることで平面回路に変換する。
-
\(\textsc{1-In-3SAT}\):「3CNF 式が与えられる。変数への真偽値割り当てであって全ての節がちょうど一つの \(\textsc{True}\) リテラルを持つようなものは存在するか?」NP 困難性の証明は一般的な \(\textsc{3SAT}\) からの帰着で行われる。
-
\(\textsc{NotAllEqual3SAT}\):「3CNF 式が与えられる。変数への真偽値割り当てであって全ての節が少なくとも一つの \(\textsc{True}\) リテラルと少なくとも一つの \(\textsc{False}\) リテラルを持つようなものは存在するか?」NP 困難性の証明は一般的な \(\textsc{3SAT}\) からの帰着で行われる。
-
\(\textsc{Planar3SAT}\):「与えられた平面 3CNF 式は充足可能か?」ここで 3CNF 式 \(\Phi\) が平面であるとは、頂点が \(\Phi\) の変数と節に対応し、変数と節の間に辺があるのが \(\Phi\) において節がその変数 (またはその否定) をリテラルとして持つときに限られるような二部グラフが平面グラフであることを言う。NP 困難性の証明は \(\textsc{PlanarCircuitSAT}\) からの帰着で行われる13。
-
\(\textsc{Exact3Dimenstional}\)\(\textsc{Matching}\) あるいは \(\textsc{X3M}\):「集合 \(S\) と \(S\) の要素の三つ組の集合が与えられる。三つ組の集合の部分集合であって \(S\) を重複なく被覆するようなものは存在するか?」NP 困難性の証明は \(\textsc{3SAT}\) からの帰着で行われる (3 が入っているから)。
-
\(\textsc{Partition}\):「\(n\) 個の整数の集合 \(S\) が与えられる。\(A \cup B = S\) かつ \(A \cap B = \varnothing\) を満たす \(S\) の分割 \((A, B)\) であって \[ \sum_{a \in A} a = \sum_{b \in B} b \] となるものは存在するか?」NP 困難性の証明は \(\textsc{SubsetSum}\) からの簡単な帰着で行われる。\(\textsc{Partition}\) は \(\textsc{SubsetSum}\) と同じように弱 NP 困難である。
-
\(\textsc{3Partition}\):「\(3n\) 個の整数の集合 \(S\) が与えられる。\(S\) を互いに重ならない \(n\) 個の三つ組に分け、かつ全ての三つ組の和が等しくなるようにすることは可能か?」名前は似ているが、この問題は \(\textsc{Partition}\) とは大きく異なる (名前を付けたのは私ではありませんから、許してください)。NP 困難性の証明は \(\textsc{X3M}\) からの帰着で行われる (3 が入っているから)。\(\textsc{Partition}\) と違って \(\textsc{3Partition}\) は強 NP 困難であり、入力の数字が全て \(n^{3}\) 以下であったとしても NP 困難となる。
-
\(\textsc{SetCover}\):「集合の集合 \(\pmb{S} = \lbrace S_{1}, S_{2}, \ldots, S_{m} \rbrace\) が与えられる。和集合が \(\bigcup_{i} S_{i}\) と等しくなるような最小の \(S_{i}\) の集合は何か?」この問題は \(\textsc{VertexCover}\) および \(\textsc{X3M}\) の一般化である。
-
\(\textsc{HittingSet}\):「集合の集合 \(\pmb{S} = \lbrace S_{1}, S_{2}, \ldots, S_{m} \rbrace\) が与えられる。\(\bigcup_{i} S_{i}\) の部分集合であって全ての \(S_{i}\) の要素を一つ以上持つものの大きさの最小値は何か?」この問題は \(\textsc{VertexCover}\) の一般化である。
-
\(\textsc{LongestPath}\):「辺に非負の重みの付いたグラフ \(G\) (無向でも有向でもよい) とその頂点 \(u, v\) が与えられる。\(u\) から \(v\) への最長の単純路は何か?」単純路とは同じ頂点を二度以上通らない路を言う。この問題は \(\textsc{HamiltonianPath}\) の一般化である。もちろん最短路問題ならば多項式時間で解ける。
-
\(\textsc{SteinerTree}\):「辺に重みの付いた無向グラフ \(G\) が与えられ、いくつかの頂点に印が付いている。印の付いた全ての頂点を含む \(G\) の部分木のうち最小のものは何か?」全ての頂点に印が付いているときの Steiner 木はただの最小全域木であり、印が二つの頂点だけに付いているときの Steiner 木は二つの頂点の間の最短路である。NP 困難性の証明は \(\textsc{VertexCover}\) からの帰着で行われる。
-
\(\textsc{Max2SAT}\):「各節が二つのリテラルからなる CNF のブール式が与えられる。変数の真偽値割り当ての中で \(\textsc{True}\) を一つ以上持つ節の数を最大化するものは何か?」NP 困難性の証明は \(\textsc{3SAT}\) からの帰着で行われる (3 が入っていないのに!)。\(\textsc{Max2SAT}\) を単純にした「与えられた 2CNF 式は充足可能か?」という問題は多項式時間で解ける。
-
\(\textsc{MaxCut}\):「無向グラフ \(G = (V,E)\) が与えられる。\(S \subseteq V\) の中で端点の一方だけが \(S\) に含まれる辺の数を最大化するものは何か?」 \(G\) に含まれる最大の二部グラフを見つける問題とも言える。NP 困難性の証明は \(\textsc{Max2SAT}\) からの帰着で行われる。
これまでに示した例は有用であるものの無味乾燥に感じられますが、人気のあるパズルや一人用ゲームの中にも NP 困難であることが示されているものや、一般化したものが NP 困難となることが示されているものが多くあります (NP 困難ですらないパズルは間違いなく退屈でしょう!)。あなたが知っているであろう例をいくつかあげます:
-
マインスイーパー (\(\textsc{CircuitSAT}\) からの帰着)14
-
数独 (最終的には \(\textsc{3SAT}\) からの帰着)15
-
テトリス (\(\textsc{3Partition}\) からの帰着)16
-
クロンダイク、またの名を "ソリティア" (\(\textsc{3SAT}\) からの帰着)17
-
パックマン (\(\textsc{HamiltonianCycle}\) からの帰着)18
-
スーパーマリオブラザーズ (\(\textsc{3SAT}\) からの帰着)19
-
キャンディクラッシュソーダ (\(\textsc{3SAT}\) の変種からの帰着)20
-
Threes/2048 (\(\textsc{3SAT}\) からの帰着)21
-
\(n \times n \times n\) のルービックキューブの最短解 (\(\textsc{HamiltonianCycle}\) からの帰着)22
-
クッキークリッカー (\(\textsc{Partition}\) と \(\textsc{3Partition}\) からの帰着)23
脚注の制限により、このリストは不完全です24。2019 年 6 月現在、Ultimate Paperclips, Line Rider, Twister, Cards Against Humanity を一般化したものを NP 困難だと証明した人は誰もいませんが、時間の問題でしょう。
正しい問題を選ぶ
問題の NP 困難性を証明するうえで最も難しいステップの一つは、帰着元となるのに適した問題を選ぶ部分です。Cook-Levin の定理からは、ある NP 困難な問題から問題 \(X\) への帰着があるならば、任意の NP 困難な問題から問題 \(X\) への帰着が存在することが言えます。しかしそうは言っても帰着のしやすさは問題によって異なります。問題を選ぶ機械的な方法というのは存在しませんが、役に立つであろう経験則をいくつかあげます:
-
問題がオブジェクトにビットを割り当てたり、集合の部分集合を選んだり、集合を二つに分割したりしていたら、\(\textsc{SAT}\) あるいは \(\textsc{Partition}\) の何らかのバージョンからの帰着を試してみる。
-
問題がラベル (大きさが固定の小さな集合から選ぶもの) を割り当てたり、集合を小さな部分集合に分割していたら、\(k \textsc{Color}\) あるいは \(\textsc{3Color}\) からの帰着を試してみる。
-
問題が何かを特定の順番に並べていたら、\(\textsc{DirectedHamCycle}\) や \(\textsc{Directed}\)\(\textsc{HamPath}\) あるいは \(\textsc{TravelingSalesman}\) からの帰着を試してみる。
-
問題が何らかの制約を満たす大きな部分集合を見つけようとしていたら、\(\textsc{MaxIndSet}\), \(\textsc{MaxClique}\), \(\textsc{Max2SAT}\) からの帰着を試してみる。
-
問題が集合をたくさんの小さな部分集合へと分割しようとしていたら、\(\textsc{3Partition}\) からの帰着を試してみる。
-
問題に \(3\) という数字が自然に出現するなら、\(\textsc{3SAT}\), \(\textsc{3Color}\), \(\textsc{X3M}\), \(\textsc{3Partition}\) からの帰着を試してみる (ふざけてなんかいません)。
-
どれもダメだったら、\(\textsc{3SAT}\) あるいは \(\textsc{CircuitSAT}\) だって試す!
\(\textsc{Tetris}\) あるいは \(\textsc{SuperMarioBros}\) または \(\textsc{TrainYard}\) を帰着元として使うのはお勧めしません。あなたが選ぶべきなのは、問題を難しくしている何らかの特徴を捉えながらもできるだけ単純であるような問題です。
ちょっとした現実世界の例
ドラフツ (draughts) は何千年にもわたって遊ばれているボードゲームです。ドラフツには様々なバージョンがありますが、アメリカ人の多くにとってはチェッカー (checker) あるいはイングリッシュドラフツ (English draughts) と呼ばれるものが一番身近でしょう。しかし世界で一番知られているバージョンは国際ドラフツ (international draughts) あるいはポーランドドラフツ (Polish draughts) と呼ばれるものであり、16 世紀のオランダに起源を持ちます。完全なルールについては Wikipedia に譲り、英米バージョンとの主な違いをここに示します:
-
空飛ぶキング: チェッカーと同じように、相手の陣地の一番奥まで進んだ駒はキングになり、後ろに進むことができるようになる。ただしチェッカーと異なり、キングは斜め方向にいくらでも進むことができる。キングは相手の駒を一つだけ飛び越して移動でき、飛び越された相手の駒は盤から取り除かれる。
-
必ず最も多く取る: それぞれのターンにおいて、プレイヤーは取り除かれる相手の駒の数が最大になるように駒を動かさなければならない。通常のチェッカーには駒を動かした後にさらに駒を取れるなら必ず動かすというルールがあるが、国際ドラフツのルールはこれと異なる。つまり、チェッカーでは取り除かれる駒の数が必ず極大値となるのに対して、国際ドラフツでは取り除かれる駒の数が必ず全ての手の中の最大値となる。
-
駒を取り除くときの動作: チェッカーと同じように、駒が取り除かれるのはターンの終わりである。一つの駒が取り除かれるのは一回だけなので、一度飛び越された駒はそのターンの終わりまで飛び越すことができない障害物として盤に残る。
例えば次に示す初期状態において円が普通の駒を、二重の円がキングを表しているとすると、黒は必ず図に示された動きを行わなければなりません。この動きで黒が取り除くことになる白い駒の数 \(5\) が他のどんな動きよりも多いからです。黒の駒が 5 個の駒を取った後に動きをこれ以上続けられないのは、一度取った駒はターンが終わるまで盤に残ったままであるためです。その後白は図に示された動きを必ず行わなければならず、この動きによって白が勝利します。
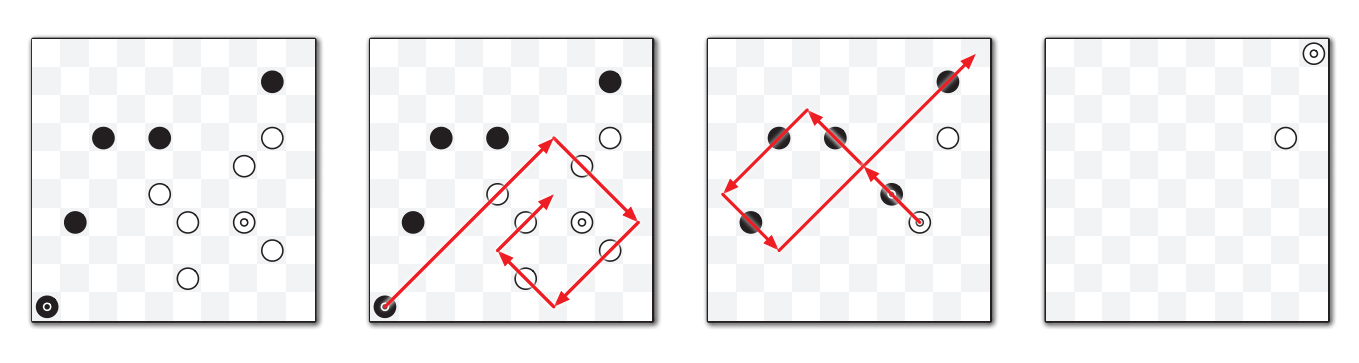
実際のゲームは \(10 \times 10\) の盤と双方 20 個ずつの駒を使って行いますが、この設定では任意のゲームが計算機的に自明になってしまいます。つまり、任意の盤面に対する可能な手をあらかじめ計算して定数サイズのルックアップテーブルに格納しておくことで、次の盤面の計算が定数時間で行えるということです。もちろん定数は巨大になりますが、定数であることに違いはありません!
しかし国際ドラフツを \(n \times n\) に自然に拡張した場合、合法な手を見つけることが NP 困難になります! 次に説明するのは 2010 年に Bob Hearn によって発見された25 有向グラフにおけるハミルトン閉路問題からの帰着です。ほとんどの二人対戦ゲームにおいては最良の手を見つける問題が NP 困難に (あるいはそれ以上に難しく) なりますが、ルールに従うだけで NP 困難となってしまうゲーム ――さらに言えば、何世紀にもわたって遊ばれているゲーム―― というのは私はこれしか知りません!
\(n\) 頂点の無向グラフ \(G\) が与えられたと仮定して、国際ドラフツの盤面であって \(G\) にハミルトン閉路が存在するときに限って白が指定された数の黒の駒を取れるものをこれから構築します。\(G\) の頂点に適当な順番で \(1\) から \(n\) まで番号を振り、\(G\) の無向辺 \(uv\) を \(u \rightarrow v\) と \(v \rightarrow u\) に分けることで \(G\) を有向グラフとして考えます。構築するドラフツの盤面はいくつかのガジェットからなります:
-
\(G\) の頂点はウサギの顔の形をした頂点ガジェットで表される。頂点ガジェットは水平に一列に並び、各辺 \(i \rightarrow j\) は頂点ガジェット \(i\) の "右耳" と頂点ガジェット \(j\) の "左耳" を結ぶ直角に交わる二つの線分で表される。弧 \(i \rightarrow j\) は \(i < j\) ならば頂点ガジェットの上に、\(i > j\) ならば頂点ガジェットの下に引かれる。
-
頂点ガジェットの下半分はダイアモンドの形をした "金庫" である。金庫には図中で灰色の円で示されている壁があり、二つの黒い駒の層からなっているので飛び越えることができない。金庫の中には \(N\) 個の黒い駒があり、白のキングは一度に全てを飛び越えることができる (\(N\) は大きな整数であり、値は後で指定する)。白のキングは金庫の "右耳" から入り、内部にある駒を全て飛び越し、"左耳"から出ていくことができる。両方の耳には駒が通ることのできる通路があり、この通路の壁も駒二つ分の厚さがある。通路には白いキングが侵入するための隙間がいくつか空いており、"耳" の長さは他のガジェットの数によって決まる。
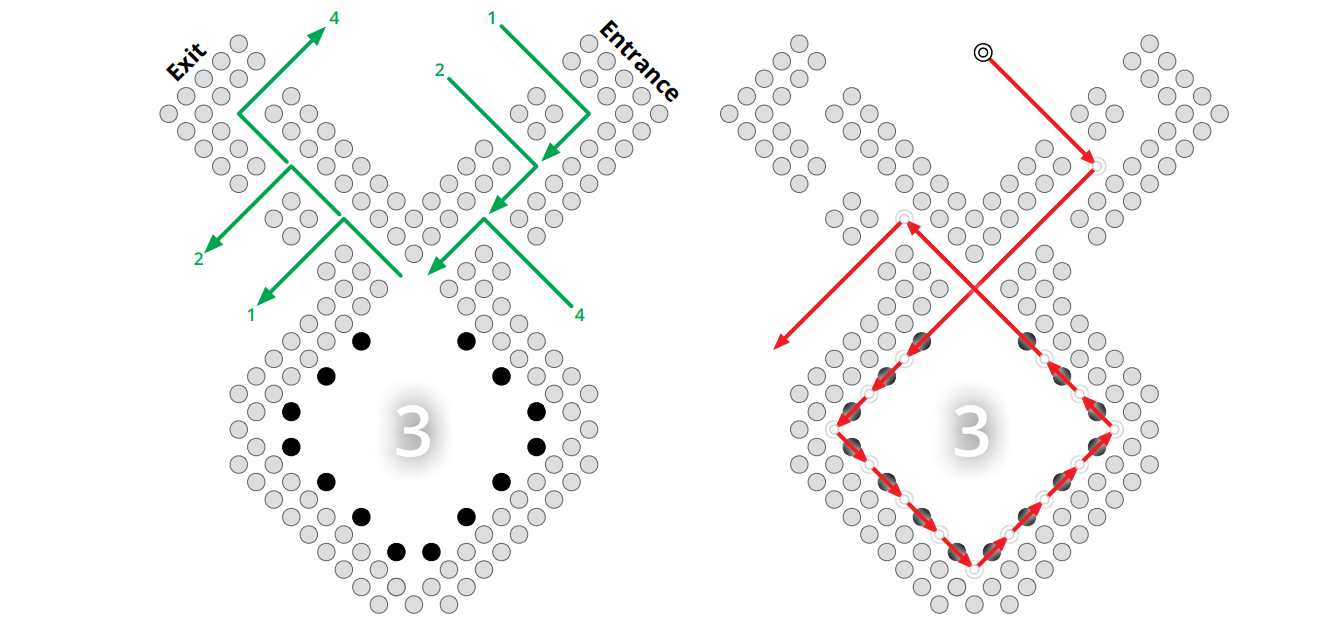 図 12.20左: 三つの入口と三つの出口を持つ頂点ガジェット。右: 金庫を空にする白いキング。灰色の円は飛び越すことができない黒い駒を表す。
図 12.20左: 三つの入口と三つの出口を持つ頂点ガジェット。右: 金庫を空にする白いキング。灰色の円は飛び越すことができない黒い駒を表す。 -
任意の弧 \(i \rightarrow j\) について、白いキングが \(i\) から \(j\) へと方向転換するための曲がり角ガジェットが置かれる。
-
二つの弧が交わる場所には交差点ガジェットが置かれる。このガジェットは白いキングが弧をたどるのを妨げないが、交差するもう一方の弧に進むことを許さない。
 図 12.21左: 曲がり角ガジェットに対する二つある路のうち一つ。右: 交差点ガジェットに対する二つある路のうち一つ。
図 12.21左: 曲がり角ガジェットに対する二つある路のうち一つ。右: 交差点ガジェットに対する二つある路のうち一つ。
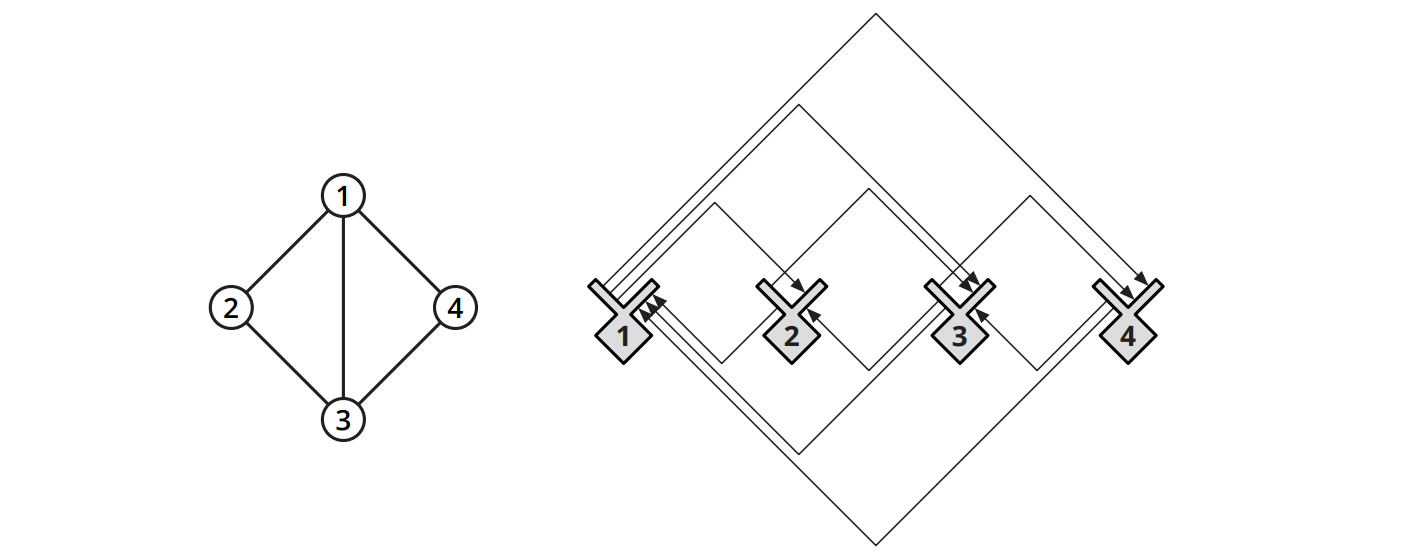
初期盤面では一つの白いキングはいずれかの金庫の下部に置かれ、弧をたどって金庫を空にしていく動きを行えます。\(G\) のハミルトン閉路の逆も \(G\) のハミルトン閉路なので、ガジェットの入口と出口を反転させても構いません。
\(G\) がハミルトン閉路を持つ場合、白いキングは全ての金庫を訪れて最低でも \(nN\) 個の駒を飛び越したうえでスタート地点に戻ってくることができます。一方 \(G\) がハミルトン閉路を持たない場合には、白いキングは少なくともスタート地点の金庫にある黒い駒の半分を飛び越えることができないので、全体で飛び越えることになる黒い駒の数は最大でも \((n - 1 / 2)N + O(n^{3})\) 個となります。ここで \(O(n^{3})\) は曲がり角ガジェットと交差点ガジェットの分です (任意の弧には一つの曲がり角ガジェットと最大 \(n^{2} / 2\) 個の交差点ガジェットが含まれます)。
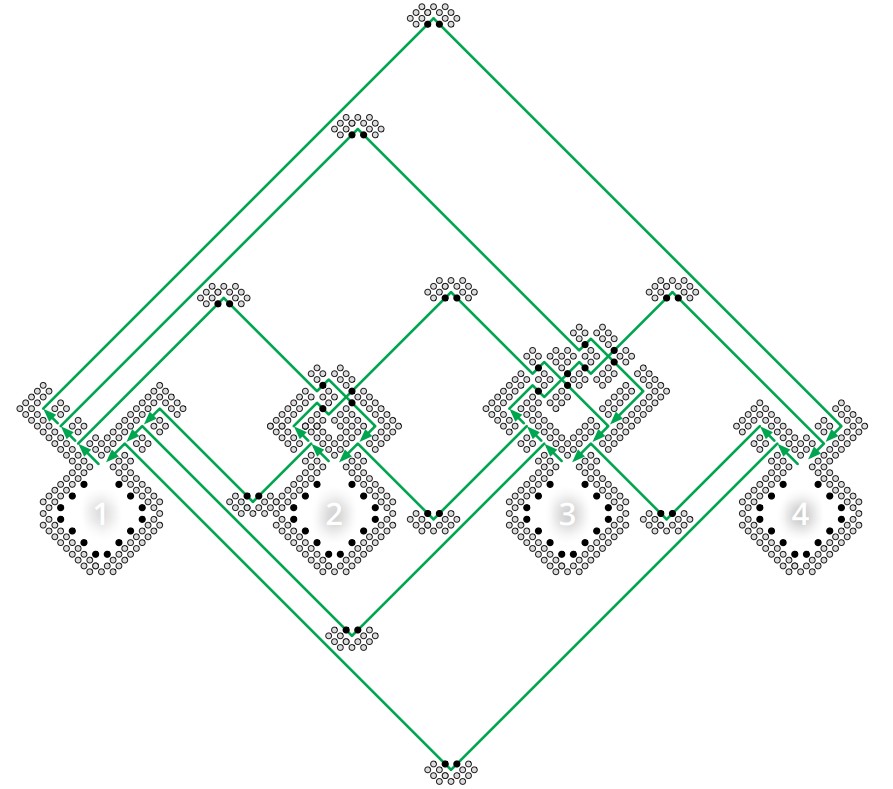
以上より \(N=n^{4}\) とすれば帰着が完成します。全体としては \(O(n^{5}) \times O(n^{5})\) の盤面となり、\(O(n^{5})\) 個の黒い駒と一つの白いキングを含みます。この構築は総当たりを使っても多項式時間で行えます。完全な盤面の例を次に示します。なお次の問題が NP 困難であるかどうかは未解決です: 「\(n \times n\) の国際ドラフツの盤面が与えられる。白は黒い駒を全て飛び越すことができる (そしてルール上必ずそうすることになる) か?」
❤ 縞模様を超えて
P と NP は複雑性クラスの巨大な階層における最初の二ステップでしかありません。この章 (そしてこの本) の締めくくりとして、興味深い複雑性クラスをいくつか紹介します。
多項式空間
PSPACE は多項式空間を使って解ける判定問題の集合です。NP に属する全ての問題 (したがって P に属する全ての問題) は PSPACE に属します。NP \(\neq\) PSPACE であることが広く信じられていますが、P \(\neq\) PSPACE さえ証明できた人はいません。
問題 \(\Pi\) がPSPACE 困難 (PSPACE-hard) であるとは、多項式空間を使って解ける任意の問題 \(\Pi^{\prime}\) について \(\Pi^{\prime}\) から \(\Pi\) への多項式時間多対一帰着が存在することを言います。PSPACE 困難な問題が一つでも NP に属すれば PSPACE=NP であり、同様に PSPACE 困難な問題が一つでも P に属すれば P=PSPACE です。
一番重要な PSPACE 困難問題は量化子付きブール式問題 (quantified boolean formula problem, \(\textsc{QBF}\)) です。これは任意の数の全称量化子および存在量化子のついた自由変数を含まないブール式 \(\Phi\) が \(\textsc{True}\) に等しいかを判定する問題であり、例えば \(\textsc{SAT}\) は存在量化子だけを含む \(\textsc{QBF}\) の特殊ケースとみなすことができます。また次の式は \(\textsc{QBF}\) への正しい入力です: \[ ∃a: ∀b: ∃c: (∀d : a ∨ b ∨ c ∨ \overline{d}) ⇔ ((b ∧ \overline{c}) ∨ (∃e : \overline{(\overline{a} ⇒ e)} ∨ (c \neq a ∧ e))) \] \(\forall\) と \(\exists\) が一つずつ交互に式の先頭にだけついている連言標準形の式だけを考えたとしても、\(\textsc{QBF}\) は PSPACE 困難となります。例えば次の式です: \[ ∃a: ∀b: ∃c: ∀d :(a ∨ b ∨ c) ∧ (b ∨ \overline{c} ∨ \overline{d}) ∧ (\overline{a} ∨ c ∨ d) ∧ (a ∨ \overline{b} ∨ \overline{d}) \]
この制限されたバージョンの QBF は二人のプレイヤーの間の質問ゲームとしても表現できます。つまり二人のプレイヤー Alice と Bob に自由変数 \(x_{1}, x_{2}, \ldots, x_{n}\) を持つ 3CNF 式が与えられ、二人が交互に変数に真偽値を割り当てていくというゲームです ――まず Alice が \(x_{1}\) に割り当て、次に Bob が \(x_{2}\) に割り当て、以下同様です。Alice は式全体が \(\textsc{True}\) になるように値を割り当て、Bob は式全体が \(\textsc{False}\) になるように変数に値を割り当てます。Alice と Bob が完璧にプレイするという仮定の下で誰が勝つかを答える問題は、\(\textsc{QBF}\) と同じ問題になります。
驚くことではないかもしれませんが、三目並べ、オセロ、チェッカー、囲碁、チェス、マンカラなどのほとんどの二人対戦ゲーム26 ――正確にはこれらのゲームを任意に大きい盤で遊べるようにしたもの―― は PSPACE 困難です。
もう一つの重要な PSPACE 困難問題は NFA の全域性です:「あるアルファベット \(\Sigma\) 上の非決定性有限状態オートマトン \(M\) が与えられたとする。\(M\) は \(\Sigma^{\ast}\) に含まれる全ての文字列を受理するか?」という問題です。NFA の同値性 (「二つの NFA は同じ言語を受理するか?」) と NFA の最小化 (「ある NFA と同じ言語を受理する最小の NFA は何か?」) という似た問題もまた PSPACE 困難であり、これらの問題に対応する正規表現の問題も PSPACE 困難となります (決定性有限状態オートマトンに対する同じ問題は多項式時間で解けます)。
指数時間
次に紹介する巨大な複雑性クラスは、指数時間で解ける判定問題を集めた EXP (あるいは EXPTIME) です。これはある \(c > 0\) があって \(2^{n^{c}}\) ステップで問題が解けることを意味します。PSPACE に含まれる全ての問題 (したがって NP に含まれる全ての問題 (したがって P に含まれる全ての問題)) は EXP にも属します。PSPACE \(\subsetneq\) EXP であると広く信じられていますが、NP \(\neq\) EXP さえ証明できた人はいません。
問題 \(\Pi\) がEXP 困難 (EXP-hard) であるとは、指数時間を使って解ける任意の問題 \(\Pi^{\prime}\) について \(\Pi^{\prime}\) から \(\Pi\) への多項式時間多対一帰着が存在することを言います。EXP 困難な問題が一つでも PSPACE に属すれば EXP=PSPACE であり、同様に EXP 困難な問題が一つでも NP に属すれば EXP=NP です。ただし P \(\neq\) EXP であることは分かっているので、EXP 困難な問題は P に属しません。
興味深い二人対戦ゲームの多く ――チェッカー、チェス、マンカラ、囲碁など―― を一般化したものは EXP 困難となりますが、PSPACE 困難と EXP 困難の境界はとても繊細です。例えば通常の \(8 \times 8\) のチェスには引き分けになる状況が三種類あります:
- ステールメイト (チェックされていないプレイヤーに合法手が無い)
- 三度同じ盤面になる
- 50 手の間両者の駒が取られない
\(n \times n\) に一般化したチェスが PSPACE 困難かそれとも EXP 困難かはこの引き分けのルールをどう一般化するかによって変化します。例えば \(n^{3}\) 手の間両者の駒が取られなければ引き分けというルールを採用した場合、全てのゲームが多項式回の手で終了するので、多項式空間だけを使って全てのゲームをシミュレートできます。一方で、両者が駒を取らない状況がどれだけ長く続いても引き分けにならないというルールを採用した場合、一つのゲームが指数回の手に及ぶことになり、多項式空間だけでは同じ盤面になったかどうかを検出できません。実はこのバージョンの \(n \times n\) チェスは EXP 困難となります。
もっと高く!
もちろん、指数時間だって話の終わりではありません。 NEXP は非決定的指数時間で解ける判定問題の集合です。NEXP に含まれる問題の答えが \(\textsc{Yes}\) であるインスタンスには答が \(\textsc{Yes}\) であることの証明が存在して、その証明が指数時間で検証できるということです。 EXPSPACE は指数空間を使って解ける判定問題の集合です。これらの巨大な複雑性クラスにさえ困難な問題が存在します。例えば正規表現に交差演算子 \(\cap\) を加えた場合、二つの正規表現が同じ言語を表しているかどうかを判定する問題は EXPSPACE 困難です。
EXPSPACE よりも大きな複雑性クラスも存在し、資源の制限が二重指数 (doubly-exponential) であるもの (EEXP, NEEXP, EEXPSPACE)、三重指数 (triply-exponential) であるもの (EEEXP, NEEEXP, EEEXPSPACE) と無限に続きます。
ここまでに話してきた複雑性クラスは包含関係による順序を持ちます: \[ \text{P} ⊆ \text{NP} ⊆ \text{PSPACE} ⊆ \text{EXP} ⊆ \text{NEXP} ⊆ \text{EXPSPACE} ⊆ \text{EEXP} ⊆ \text{NEEXP} ⊆ ··· \] ほとんどの複雑性理論研究者はこれら包含関係全てが真の包含関係である、つまりどの二つの複雑性クラスも同じではないと強く信じています。しかし、これまでに示された一番強い結果でも、この並びで三つ離れたクラスが異なることを示すに留まっています。例えば P \(\neq\) EXP および PSPACE \(\neq\) EXPSPACE は示されていますが、P \(\neq\) PSPACE および NP \(\neq\) EXP は示されていません。
指数を使って表せる複雑性クラスの増加列の極限は ELEMENTARY と呼ばれる複雑性クラスであり、このクラスは時間または空間の使用量が定数 \(k\) を使って \(2 \uparrow^{k} n\) で抑えられる判定問題の集合として定義できます。ここで \[ 2 \uparrow^{k} n := \begin{cases} n & \text{if } k = 0 \\ 2^{2 \uparrow^{k-1} n} & \text{それ以外} \end{cases} \] であり、例えば \(2 \uparrow^{1} n = 2^{n}\) および \(2 \uparrow^{2} n = 2^{2^{n}}\) です。
全ての自然な判定問題がこの初等時間 (elementary time) で解けると思いたくなるかもしれませんが、そうではありません。拡張正規表現と呼ばれる、 (空でも構わない) アルファベットを結合 (\(xy\))、和集合 \(x + y\)、Kleene 閉包 (\(x^\ast\))、否定 (\(\overline{x}\)) で組み合わせたものを考えます。例えば \(\overline{({\color{maroon}{0}} + {\color{maroon}{1}})^{\ast} \color{maroon}{00} ({\color{maroon}{0}}+{\color{maroon}{1}})^{\ast}}\) という拡張正規表現は \(\lbrace {\color{maroon}{0}}, {\color{maroon}{1}} \rbrace\) が並んだ文字列であって \({\color{maroon}{0}}\) が連続して出現しないものを表します。二つの拡張正規表現が表す言語が等しいかどうかをアルゴリズムを使って判定するのは可能であり、具体的には二つの拡張正規表現を同値な NFA で表し、DFA に変換し、DFA を最小化して比べれば判定できます。しかしこのアルゴリズムの実行時間は式の中に否定が出現するたびに指数的に増加するので \(2 \uparrow^{\Theta(n)} 2\) であり、初等的ではありません。1974 年の Larry Stockmeyer (ラリー・ストックメイヤー) の証明によると、Kleene 閉包を使用を禁止したとしてもこの問題は初等時間で解くことができません!
練習問題
-
-
\(\textsc{Partition}\) を \(O(nM)\) 時間で解くアルゴリズムを説明、解析してください。ここで \(n\) は入力の集合の大きさ、\(M\) は入力の集合の要素の和を表します。
-
このアルゴリズムが P=NP を意味しないのはなぜですか?
-
-
\(\textsc{BoxDepth}\) と呼ばれる次の問題を考えます:「辺が \(x, y\) 軸に平行な \(n\) 個の長方形の集合が与えられる。共通する点が存在するようなこの集合の部分集合で最大のものの大きさはいくつか?」
-
\(\textsc{BoxDepth}\) から \(\textsc{MaxClique}\) への多項式時間帰着を説明してください。
-
\(\textsc{BoxDepth}\) に対する多項式時間アルゴリズムを説明、解析してください。 [ヒント: 簡単に得られるのは \(O(n^{3})\) 時間のアルゴリズムですが、\(O(n\log n)\) 時間のアルゴリズムもあります。]
-
この二つの結果から P=NP と結論できないのはなぜですか?
-
-
論理式が選言標準形 (disjunctive normal form, DNF) であるとは、式がいくつかの項 (term) の選言 (\(\textsc{Or}\)) であり、それぞれの項が一つ以上のリテラルの連言 (\(\textsc{And}\)) であることを言います。例えば \[ (\overline{x} ∧ y ∧ \overline{z}) ∨ (y ∧ z) ∨ (x ∧ \overline{y} ∧ \overline{z}) \] は選言標準形の論理式です。\(\textsc{DNF-SAT}\) とは選言標準形の式が入力として与えられたときに、その式が充足可能かを判定する問題です。
-
\(\textsc{DNF-SAT}\) に対する多項式時間アルゴリズムを説明してください。
-
次に示す P=NP の "証明" はどこが間違っていますか?
全ての節に最大でも三つしかリテラルを含まない連言標準形の式が与えられ、その式が充足可能かどうかを知りたいとする。
分配法則を使えば与えられた式を選言標準形に変換できる。例えば \[ \begin{aligned} & (x ∨ \overline{y} ∨ \overline{z}) ∧ (\overline{x} ∨ \overline{y}) \\ & \iff (x ∧ \overline{y}) ∨ (y ∧ \overline{x}) ∨ (\overline{z} ∧ \overline{x}) ∨ (\overline{z} ∧ \overline{y}) \end{aligned} \] となる。(a) のアルゴリズムを使えばこの DNF 式が充足可能であるかどうかを多項式時間で判定できるので、NP 困難である \(\textsc{3Sat}\) を多項式時間で解くことができる。よって P=NP でなければならない!
-
-
\(\textsc{AllOrNothing3SAT}\) は与えられた 3CNF 論理式について、変数への真偽値割り当てであって任意の節が三つの \(\textsc{True}\) リテラルを持つか、そうでなければ三つの \(\textsc{False}\) リテラルを持つようなものが存在するかを判定する問題です。
-
\(\textsc{AllOrNothing3SAT}\) を解く多項式時間アルゴリズムを説明してください。
-
しかし \(\textsc{3SAT}\) は NP 困難です! (a) のアルゴリズムが P=NP を意味しないのはどうしてですか?
-
-
-
任意の重み付きグラフの最短ハミルトン閉路の長さを多項式時間で計算する魔法のブラックボックスが与えられたとします。このブラックボックスをサブルーチンとして使って、任意の重み付きグラフのハミルトン閉路を計算する多項式時間アルゴリズムを説明、解析してください。
-
任意のグラフ \(G\) を入力として受け取って \(G\) に含まれる最大の完全部分グラフの大きさを多項式時間で出力する魔法のブラックボックスが与えられたとします。このブラックボックスをサブルーチンとして使って、任意のグラフの最大の完全部分グラフを計算する多項式時間アルゴリズムを説明、解析してください。
-
任意のグラフが 3-彩色可能かどうかを多項式時間で判定する魔法のブラックボックスが与えられたとします。このブラックボックスをサブルーチンとして使って、与えられた任意のグラフの 3-彩色を計算するか、そのグラフの 3-彩色は不可能であると正しく報告する多項式時間アルゴリズムを説明、解析してください。 [ヒント: ブラックボックスへの入力はグラフだけです。頂点と辺からなるグラフだけであり、他には何も入力しません。]
-
任意の論理式が充足可能かどうかを多項式時間で判定する魔法のブラックボックスが与えられたとします。このブラックボックスをサブルーチンとして使って、与えられた任意の論理式を充足させる真偽値割り当てを計算するか、その式は充足不可能であると正しく報告する多項式時間アルゴリズムを説明、解析してください。
-
任意の整数の集合 \(X\) を入力として受け取って、\(X\) を \(A, B\) に分割して \(\sum A = \sum B\) とできるかどうかを多項式時間で出力する魔法のブラックボックスが与えられたとします。このブラックボックスをサブルーチンとして使って、与えられた任意の整数の集合を和の等しい二つの部分集合に分割するか、そのような分割は不可能であると正しく報告する多項式時間アルゴリズムを説明、解析してください。
-
♣ ❤ 任意の拡張正規表現 (定義は本文を参照) \(R\) を入力として受け取って、\(R\) とマッチする文字列が一つでもあるかどうかを多項式時間で出力する魔法のブラックボックスが与えられたとします。このブラックボックスをサブルーチンとして使って、与えられた任意の拡張正規表現とマッチする文字列を一つ計算するか、そのような文字列は存在しないと正しく報告する多項式時間アルゴリズムを説明、解析してください。
-
-
-
\(\textsc{Partition}\) から \(\textsc{SubsetSum}\) への多項式時間帰着を説明してください。
-
\(\textsc{SubsetSum}\) から \(\textsc{Partition}\) への多項式時間帰着を説明してください。
-
-
ハミルトン閉路問題には無向グラフに関するものと有向グラフに関するものという二つのバージョンがあります。この章では無向ハミルトン閉路問題が NP 困難であることの証明を二つ示しました。
-
無向ハミルトン閉路問題から有向ハミルトン閉路問題への多項式時間帰着を説明してください。帰着が正しいことを証明してください。
-
有向ハミルトン閉路問題から無向ハミルトン閉路問題への多項式時間帰着を説明してください。帰着が正しいことを証明してください。
-
無向ハミルトン閉路問題の NP 困難性を示しているのは二つの帰着のうちどちらですか?
-
-
-
\(\textsc{HamiltonianPath}\) から \(\textsc{HamiltonianCycle}\) への多項式時間帰着を説明してください。
-
\(\textsc{HamiltonianCycle}\) から \(\textsc{HamiltonianPath}\) への多項式時間帰着を説明してください。[ヒント: 多項式時間帰着はブラックボックスのサブルーチンを複数回呼んでも構いませんが、必ずそうしなければならないというわけではありません。]
-
-
\(\textsc{PlanarCircuitSAT}\) が NP 困難であることを証明してください。 [ヒント: 交差する配線に対するガジェットを構築してください。]
-
\(\textsc{NotAllEqual3SAT}\) が NP 困難であることを証明してください。
-
\(\textsc{1-In-3SAT}\) が NP 困難であることを証明してください。
-
この問題では \(\textsc{CNFSAT}\) を少しだけ変更した問題を考えます。それぞれの問題において入力は連言標準形の論理式 \(\Phi\) であり、目標は \(\Phi\) を充足させる真偽値割り当てが存在するかを判定することです。
-
\(\Phi\) の各節が最大でも三つのリテラルを含み、各変数は最大でも三つの節にしか現れないとします。このように変更した \(\textsc{CNFSAT}\) が NP 困難であることを示してください。
-
\(\Phi\) の各節がちょうど三つのリテラルを含み、各変数は最大でも四つの節にしか現れないとします。このように変更した \(\textsc{3SAT}\) が NP 困難であることを示してください。 [ヒント: (a) を先に解いてください。]
-
❤ \(\Phi\) の各節が任意の数のリテラルを含み、各変数は最大でも二つの節にしか現れないとします。このように変更した \(\textsc{CNFSAT}\) に対する多項式時間アルゴリズムを説明してください。
-
❤ \(\Phi\) の各節がちょうど三つのリテラルを含み、各変数は最大でも三つの節にしか現れないとします。このとき \(\Phi\) が充足可能なことを示してください (このように変更した \(\textsc{3SAT}\) は完全に自明な問題となります!)。
-
-
論理式が排他論理和連言標準形 (exclusive-or conjunctive normal form, XCNF) であるとは、式がいくつかの節の連言 (\(\textsc{And}\)) からなっていて、それぞれの節がリテラルの排他的論理和であることを言います。つまり、節が真となるのは真のリテラルが奇数個含まれるときだけです。\(\textsc{XCNF-SAT}\) 問題とは XCNF 式が充足可能かを判定する問題です。
\(\textsc{XCNF-SAT}\) に対する多項式時間アルゴリズムを説明するか、\(\textsc{XCNF-SAT}\) が NP 困難であることを証明してください。 [ヒント: 両方は無理です。]
-
❤ \(\textsc{3SAT}\) を少し変更した \(\textsc{Majority3SAT}\) を考えます。\(\textsc{Majority3SAT}\) の入力は \(\textsc{3SAT}\) と同じく各節がちょうど三つのリテラルを持つ連言標準形の論理式 \(\Phi\) であり、出力は \(\Phi\) の変数への真偽値割り当てであって全ての節が少なくとも二つの \(\textsc{True}\) を持つものが存在するかどうかです。
\(\textsc{Majority3SAT}\) を多項式時間で解くアルゴリズムを説明するか、\(\textsc{Majority}\)\(\textsc{3SAT}\) が NP 困難であると証明してください。 [ヒント: 両方は無理です。]
-
♠ ❤ 任意の部分集合 \(X \subset \lbrace 0, 1, 2, 3 \rbrace \) について、次の問題 (ここでは \(\textsc{X-3SAT}\) と呼びます) を考えます。入力は各節がちょうど三つのリテラルを持つ連言標準形の論理式 \(\Phi\) であり、出力は \(\Phi\) の変数への真偽値割り当てであって \(\Phi\) に含まれる \(\textsc{True}\) リテラルの数が \(X\) に含まれるものです。例えば:
-
\(\lbrace 1, 2, 3 \rbrace \textsc{-3SAT}\) は普通の \(\textsc{3SAT}\) です。
-
\(\lbrace 0, 3 \rbrace \textsc{-3SAT}\) は \(\textsc{AllOrNothing3SAT}\) です (練習問題 12.4)。
-
\(\lbrace 1, 2 \rbrace \textsc{-3SAT}\) は \(\textsc{NotAllEqual3SAT}\) です (練習問題 12.10)。
-
\(\lbrace 1 \rbrace \textsc{-3SAT}\) は \(\textsc{1-IN-3SAT}\) です (練習問題 12.11)。
-
\(\lbrace 2, 3 \rbrace \textsc{-3SAT}\) は \(\textsc{Majority3SAT}\) です (練習問題 12.14)。
\(\textsc{X-SAT}\) が多項式時間で解けるような部分集合 \(X \subset \lbrace 0,1,2,3 \rbrace\) の完全なリストを作ってください。P \(\neq\) NP を仮定してください。 [ヒント: 16 個の異なる問題を解くのはやめてください。]
-
-
-
下図 (a) のガジェットを使って、平面グラフが 3-彩色可能であるかを判定する問題が NP 困難であることを示してください。 [ヒント: ガジェットが 3-彩色可能であることを示し、任意のグラフの平面への埋め込みにおける交差をこのガジェットで適切に置き換えてください。]
-
(a) と下図 (b) のガジェットを使って、最大次数が 4 の平面グラフが 3-彩色可能であるかを判定する問題が NP 困難であることを示してください。 [ヒント: 次数が 4 よりも大きい全ての頂点を複数のガジェットを使って置き換え、全ての頂点の次数を 4 以下にしてください。]
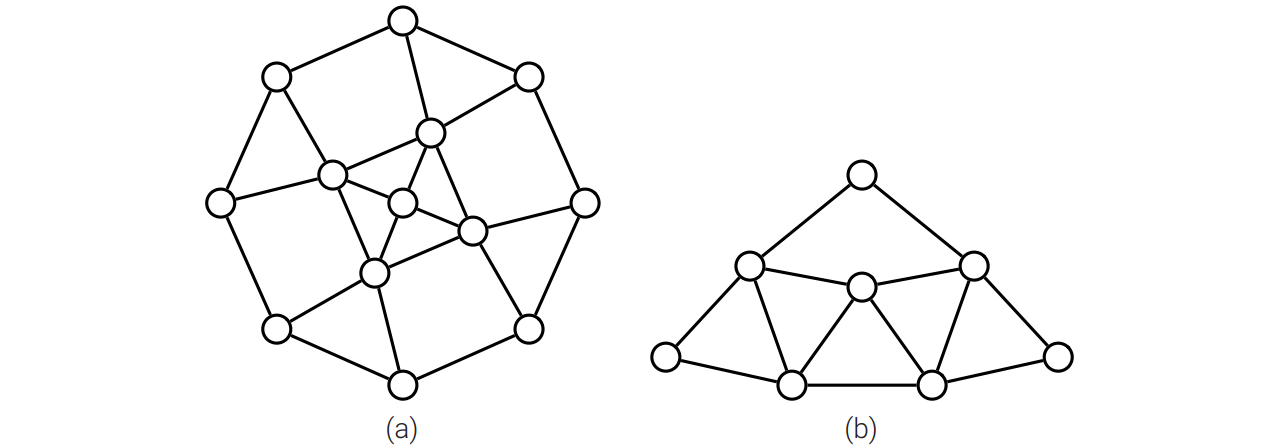
-
-
次の問題が NP 困難であることを示してください。
-
無向グラフ \(G\) が与えられる。\(G\) には 17 個の頂点を除いた全ての頂点を訪れる単純路があるか?
-
無向グラフ \(G\) が与えられる。\(G\) には全ての頂点の次数が 23 以下の全域木があるか?
-
無向グラフ \(G\) が与えられる。\(G\) には葉の数が 42 以下の全域木があるか?
-
無向グラフ \(G = (V, E)\) が与えられる。部分集合 \(S \subseteq V\) であって両端が \(S\) に含まれる \(E\) の辺の数が 374 本以下であるものの大きさの最大値はいくつか?
-
無向グラフ \(G = (V, E)\) が与えられる。部分集合 \(S \subseteq V\) であって \(S\) に含まれる任意の頂点に隣接する頂点の数が 473 個以下であるものの大きさの最大値はいくつか?
-
無向グラフ \(G\) が与えられる。最大でも 31337 本の辺だけが両端に同じ色を持つように \(G\) の頂点を三色で彩色できるか?
-
-
最小全域木問題を改変した次の問題が NP 困難であることを示してください。
-
無向グラフ \(G\) が与えられたときに、\(G\) の全域木で半径が最大のものを求める (全域木 \(T\) の半径とは \(T\) に含まれる路の長さの最大値を言う)。
-
辺に重みの付いた無向グラフ \(G\) が与えられたときに、\(G\) の深さ優先探索木の中で重みが最小のものを求める。
-
辺に重みの付いた無向グラフ \(G\) と \(G\) の頂点の部分集合 \(S\) が与えられたときに、全ての葉が \(S\) に含まれるような全域木の中で重みが最小のものを計算する。
-
辺に重みの付いた無向グラフ \(G\) と整数 \(l\) が与えられたときに、葉が \(l\) 個以下の全域木の中で重みが最小のものを計算する。
-
辺に重みの付いた無向グラフ \(G\) と整数 \(\Delta\) が与えられたときに、全ての頂点の次数が \(\Delta\) 以下の全域木の中で重みが最小なものを計算する。
-
-
3 という数字には特別な意味があります。
-
\(\textsc{2Partition}\) に対する多項式時間アルゴリズムを説明、解析してください。アルゴリズムの入力は \(2n\) 個の正の整数の集合 \(S\) であり、出力は \(S\) を \(n\) 個の互いに重ならない整数の組に分割し、その上で \(n\) 個の組の和が全て等しいようにできるかどうかです。
-
\(\textsc{2Color}\) に対する多項式時間アルゴリズムを説明、解析してください。アルゴリズムの入力は無向グラフ \(G\) であり、出力は二つの色だけを使って \(G\) を彩色できるかどうかです。
-
\(\textsc{2SAT}\) に対する多項式時間アルゴリズムを説明、解析してください。アルゴリズムの入力は各節が二つのリテラルからなる連言標準形の論理式 \(\Phi\) であり、出力は \(\Phi\) が充足可能かどうかです。 [ヒント: この問題は以前の章で説明したことと強い関連があります。]
-
-
3 という数字に特別な意味なんてありません。
-
\(\textsc{12Partition}\) 問題は次のように定義されます: 「\(12n\) 個の正の整数の集合 \(S\) が与えられたとき、 \(S\) を大きさが 12 の集合 \(n\) 個に分割し、さらに \(n\) 個の集合の和が全て等しいようにできるかを判定する」 \(\textsc{12Partition}\) が NP 困難であることを示してください。 [ヒント: \(\textsc{3Partition}\) からの帰着です。最初は多重集合を考えた方が簡単かもしれません。]
-
\(\textsc{12Color}\) 問題は次のように定義されます: 「無向グラフ \(G\) が与えられたときに、どの辺の端点も同じ色にならないように各頂点を 12 色のうちどれかで塗っていくことができるかを判定する」 \(\textsc{12Color}\) が NP 困難であることを示してください。 [ヒント: \(\textsc{3Color}\) からの帰着です。]
-
\(\textsc{12SAT}\) は次のように定義されます: 「各節にちょうど 12 個のリテラルが含まれるような連言標準形の論理式 \(\Phi\) が与えられたときに、\(\Phi\) が充足可能かどうかを判定する」 \(\textsc{12SAT}\) が NP 困難であることを示してください。 [ヒント: \(\textsc{3SAT}\) からの帰着です。]
-
-
-
\(\textsc{3SAT}\) から \(\textsc{4SAT}\) への多項式時間帰着を説明してください。
-
\(\textsc{4SAT}\) から \(\textsc{3SAT}\) への多項式時間帰着を説明してください。
-
-
❤ \(\textsc{4Color}\) から \(\textsc{3Color}\) への直接的な多項式時間帰着を説明してください (これは逆方向の帰着よりもはるかに難しいです)。
-
整数の書かれた正方形を二つつなげたものをドミノと言います27。横一列に並んだドミノの並べ方が合法であるとは、隣り合う正方形に書かれた数字が同じことを言います。
次の問題に対する多項式時間アルゴリズムを説明するか、問題が NP 困難であることを示してください。
-
ぺブリング (pebbling) は無向グラフ \(G\) を使って遊ぶ一人用ゲームです。\(G\) の各頂点にゼロ個以上の小石 (pebble) を置いた状態からゲームが始まります。プレイヤーが各手で行える唯一の操作は、適当な頂点 \(v\) を選んで \(v\) の小石を二つ取り除き、\(v\) に隣接する適当な頂点に小石を一つ追加するという操作です (もちろん二つ以上の小石の置かれた \(v\) しか選ぶことができません)。
\(\textsc{PebbleDestruction}\) 問題の入力は無向グラフ \(G = (V,E)\) と各頂点 \(v\) に対する小石の数 \(p(v)\) であり、出力は小石を最後の一つになるまで取り除く手の列です。\(\textsc{PebbleDestruction}\) が NP 困難であることを示してください。
-
無向グラフ \(G\) の 5-彩色とは、\(G\) の頂点に \(\lbrace 0,1,2,3,4 \rbrace\) のどれかの "色" を塗って、任意の辺 \(uv\) に対して \(u\) と \(v\) に違う色が割り当てられるようにする関数であることを思い出してください。5-彩色が慎重 (careful) であるとは、任意の頂点に対して隣接する頂点の色が異なっているだけではなく色の値が (mod 5 で) 2 以上離れていることを言います。無向グラフに慎重な 5-彩色が存在するかどうかを判定する問題が NP 困難であることを示してください。 [ヒント: 通常の \(\textsc{5Color}\) 問題から帰着させてください。]
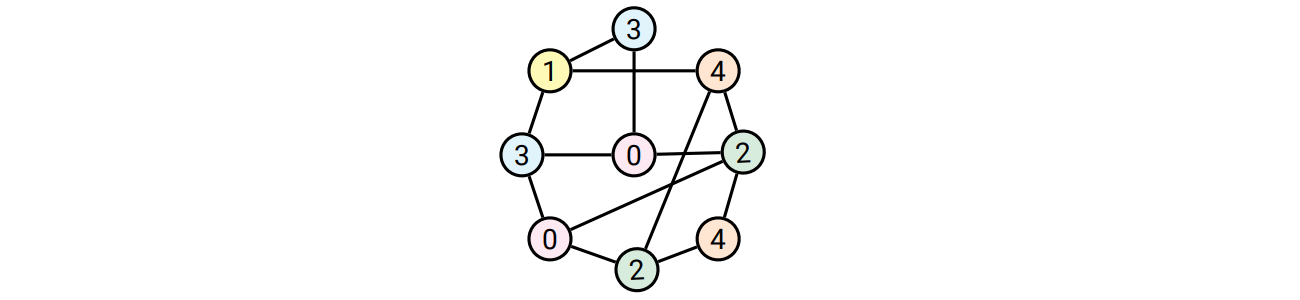 図 12.25慎重な 5-彩色
図 12.25慎重な 5-彩色 -
-
無向グラフ \(G\) の頂点の部分集合 \(S\) が半独立 (half-independent) であるとは、\(S\) の各頂点が最大でも一つの \(S\) の頂点としか隣接していないことを言います。与えられた無向グラフの最大半独立集合を求める問題が NP 困難であることを示してください。
-
無向グラフ \(G\) の頂点の部分集合 \(S\) がなんとなく独立 (sort-of-independent) であるとは、\(S\) の各頂点が最大でも 374 個の \(S\) の頂点としか隣接していないことを言います。与えられた無向グラフの最大なんとなく独立集合を求める問題が NP 困難であることを示してください。
-
無向グラフ \(G\) の頂点の部分集合 \(S\) がほぼ独立 (almost independent) であるとは、両端点が \(S\) に含まれる \(G\) の辺が 374 個以下であることを言います。与えられた無向グラフの最大ほぼ独立集合を求める問題が NP 困難であることを示してください。
-
-
無向グラフ \(G\) の頂点の部分集合 \(S\) が三角形を含まない (triangle-free) とは、任意の三つの頂点 \(u,v,w \in S\) について辺 \(uv, uw, vw\) のどれかが \(G\) に含まれないことを言います。与えられた無向グラフの含まれる三角形を含まない頂点集合の中で最大のものを見つける問題が NP 困難であることを示してください。
 図 12.26三角形を含まない大きさ 7 の頂点集合 (この集合はこのグラフに含まれる三角形を含まない頂点集合の中で最大のものではない)
図 12.26三角形を含まない大きさ 7 の頂点集合 (この集合はこのグラフに含まれる三角形を含まない頂点集合の中で最大のものではない) -
無向グラフ \(G = (V. E)\) の頂点の部分集合が支配集合 (dominating set) であるとは、\(G\) の全ての頂点が \(S\) に含まれるか 、そうでなければ \(S\) に隣接することを言います。\(\textsc{DominatingSet}\) 問題は無向グラフ \(G\) と整数 \(k\) を入力として受け取って \(G\) に大きさ \(k\) の支配集合が存在するかどうかを判定する問題です。この問題が NP 困難であることを示してください。
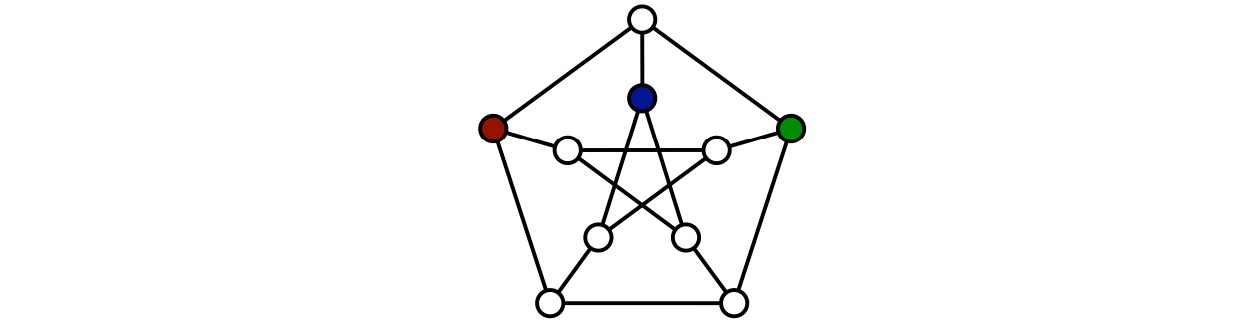 図 12.27Petersen (ピーターセン) グラフにおける大きさ 3 の支配集合
図 12.27Petersen (ピーターセン) グラフにおける大きさ 3 の支配集合 -
\(\textsc{RectangleTiling}\) 問題は次のように定義されます: 「大きな長方形といくつかの小さな長方形が与えられたときに、大きな長方形の中に小さな長方形を隙間も重なりもなく敷き詰めることができるかを判定する」
-
\(\textsc{RectangleTiling}\) が NP 困難であることを示してください。
-
\(\textsc{RectangleTiling}\) が強 NP 困難であることを示してください。
 図 12.28\(\textsc{RectangleTiling}\) 問題の答が \(\textsc{True}\) となるインスタンス
図 12.28\(\textsc{RectangleTiling}\) 問題の答が \(\textsc{True}\) となるインスタンス -
-
辺に重みの付いた無向グラフを \(G\) とします。\(G\) の重い (heavy) ハミルトン閉路とは、\(G\) の全ての頂点をちょうど一回ずつ通り抜ける閉路 \(C\) であって \(C\) の重みが \(G\) に含まれる辺の重みの和の半分より大きいものを言います。与えられたグラフが重いハミルトン閉路を持つかどうかを判定する問題が NP 困難であることを示してください。
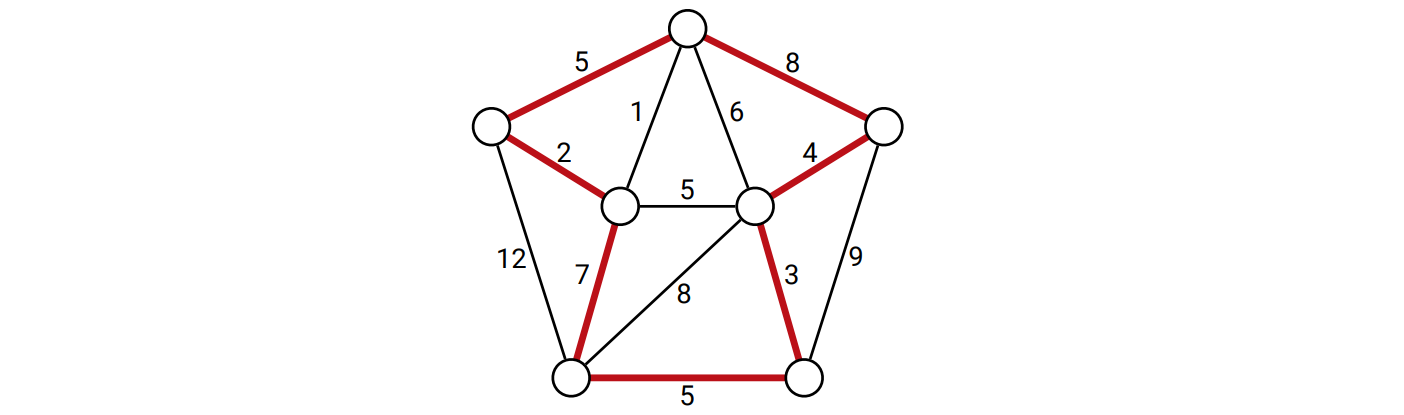 図 12.29重いハミルトン閉路 (閉路の重みは 37 であり、グラフ全体の重みは 67 である)
図 12.29重いハミルトン閉路 (閉路の重みは 37 であり、グラフ全体の重みは 67 である) -
-
無向グラフ \(G\) のトニアン路 (tonian path) とは、 \(G\) の半分以上の頂点を訪れる路のことを言います。グラフがトニアン路を含むかどうかを判定する問題が NP 困難であることを示してください。
-
無向グラフ \(G\) のトニアン閉路 (tonian cycle) とは、 \(G\) の半分以上の頂点を訪れる閉路のことを言います。グラフがトニアン閉路を含むかどうかを判定する問題が NP 困難であることを示してください。 [ヒント: (a) を使うか、あるいは使わないでください。]
-
-
-
無向グラフ \(G\) の頂点の部分集合 \(B\) が Burr (バー) 集合であるとは、\(G\) から \(B\) に含まれる頂点を全て取り除いて得られる部分グラフがハミルトン閉路を含まないことを言います。与えられた無向グラフの最小 Burr 集合を見つける問題が NP 困難であることを示してください。
-
無向グラフ \(G\) の頂点の部分集合 \(S\) が Schuyler (スカイラー) 集合であるとは、\(G\) から \(S\) に含まれる頂点を全て取り除いて得られる部分グラフがハミルトン閉路を含むことを言います。与えられた無向グラフの最大 Schuyler 集合を見つける問題が NP 困難であることを示してください。
-
-
この問題では \(\textsc{VertexCover}\) から \(\textsc{SteinerTree}\) へのとある帰着が正しいことを示します。無向グラフ \(G = (V, E)\) の最小頂点被覆を見つけたいとして、\(H = (V^{\prime}, E^{\prime})\) を次のように構築します:
-
\(V^{\prime} = V \cup E \cup \lbrace z \rbrace\)
-
\(E^{\prime} =\) \(\lbrace ve\ |\ v \in V \text{ は } e \in E \text{ の端点} \rbrace\) \(\cup \) \(\lbrace vz\ |\ v \in V \rbrace\)
この定義を言い換えると、\(G\) の各辺を頂点で置き換え、さらに新しく "先端の" 頂点 \(z\) を加えて、全ての頂点を \(z\) と結んだものが \(H\) だということです。
\(G\) に大きさ \(k\) の頂点被覆が存在するときに限って \(H\) には \(E \cup \lbrace z \rbrace\) を含む大きさ \(k\ +\) \(|E|\ +\) \(1\) の部分木が存在することを示してください。
-
-
次に示す問題に対する多項式時間アルゴリズムを説明するか、問題が NP 困難であることを示してください。
-
無向グラフ \(G\) の各辺をちょうど二回ずつ使う閉じた歩道を二重オイラー周遊 (double-Eulerian tour) と呼ぶ。無向グラフ \(G\) が与えらたとき、\(G\) は二重オイラー周遊を持つか?
-
無向グラフ \(G\) の各頂点をちょうど二回ずつ訪れる閉じた歩道を二重ハミルトン周遊 (double-Hamiltonian tour) と呼ぶ。無向グラフ \(G\) が与えられたとき、\(G\) は二重ハミルトン周遊を持つか?
-
無向グラフ \(G\) の各頂点をちょうど二回ずつ、各辺を最大でも一回ずつ訪れる閉じた歩道を二重ハミルトン回路 (double-Hamiltonian circuit) と呼ぶ。無向グラフ \(G\) が与えられたとき、\(G\) は二重ハミルトン回路を持つか?
-
無向グラフ \(G\) の各辺をちょうど三回ずつ使う閉じた歩道を三重オイラー周遊 (triple-Eulerian tour) と呼ぶ。無向グラフ \(G\) が与えらたとき、\(G\) は三重オイラー周遊を持つか?
-
無向グラフ \(G\) の各頂点をちょうど三回ずつ訪れる閉じた歩道を三重ハミルトン周遊 (triple-Hamiltonian tour) と呼ぶ。無向グラフ \(G\) が与えられたとき、\(G\) は三重ハミルトン周遊を持つか?
-
-
次の一人用ゲームを考えます。\(n \times m\) の格子のいくつかのマスに赤と青の石が置かれた状態からゲームが始まり、ゲームの目標は石をいくつか取り除いて次の条件が成り立つようにすることです:
-
どの行にも少なくとも一つの石が含まれる。
-
各列には同じ色の石しか含まれない。
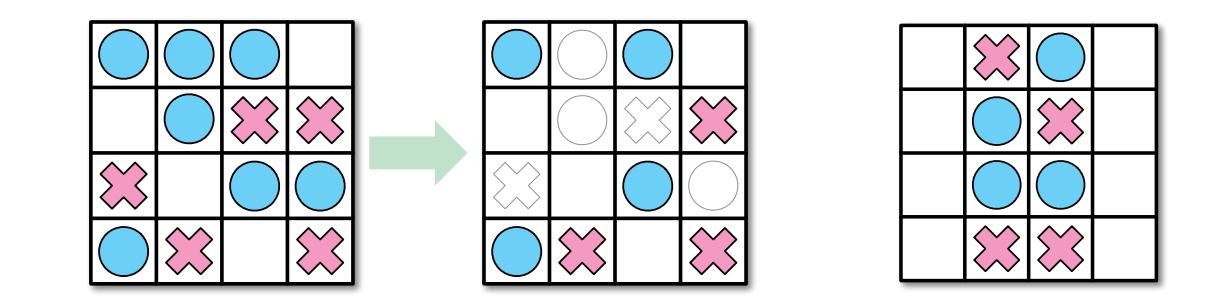 図 12.30左のパズルにはたくさんの解法があるが、右のパズルはどうやっても解けない
図 12.30左のパズルにはたくさんの解法があるが、右のパズルはどうやっても解けない青い石と赤い石の初期配置が与えられたときに、それが解けるかどうかを判定する問題が NP 困難であることを示してください。
-
-
\(n \times m\) の格子とそのマスに置くことができる石を使ったゲームを考えます。初期配置としてマスのいくつかに石が置かれた格子が与えられ、プレイヤーが行える操作はいずれかの列にある石を全て取り除くという操作だけです。
-
各行にある石の数を一つ以下にするときに、取り除くことになる列の部分集合の中で最小のものを見つける問題が NP 困難であることを示してください。
-
各行にある石の数を一つ以上に保ったまま取り除くことができる列の部分集合の中で最大のものを見つける問題が NP 困難であることを示してください。
-
❤ いくつかの列を取り除くことで、全ての行にある石の数をちょうど一つにできるかどうかを判定する問題が NP 困難であることを示してください。
-
-
Jeff は生徒が満足できるような講義をしたいと思っているので、講義の最初にどんな方針で講義を行ってほしいかを尋ねるアンケートを取っています。アンケートには講義の方針が一覧で示され、生徒はそれぞれに「こうしてほしい」、「どちらでもない」、「こうしないでほしい」 のいずれかを答えます。ただし「こうしてほしい」と「こうしないでほしい」を答えられるのは合わせて 5 回までです。Jeff の生徒はとても寛容なので、生徒が満足するのは「こうしてほしい」方針がちょうど一つ採用されたときか、そうでなければ「こうしないでほしい」方針がちょうど一つ採用されなかったときです (満足するのはこのどちらかのときだけです)。
満足する生徒の数を最大化する講義の方針を計算する多項式時間アルゴリズムを説明するか、この問題が NP 困難であると示してください。
-
あなたは地元のコミュニティシアターで開催されるミュージカルの振付師であり、劇の最後で見せる拍手喝采間違いなしのポーズを決めることになりました ("Streetcar!")。そこであなたは曲の終わりで \(n\) 人のキャストが一列に並び、手を広げて気迫に満ちた指の動き ("spirit finger") を観客に見せ付けることにしました。
しかしワンマンの監督が最後のシーンで全員が腕を真上か真下に伸ばすことを独断で決定し、さらに自身の繊細な芸術的感性を乱しかねないキャストの腕の伸ばし方をリストにして示しました。リストにはキャストの名前と腕の方向が載っており、キャストにそのような指示をすることはできません。例えば「Ned, Apu, Smithers が腕を下に出すときは Marge は腕を上に出すことができない」などと書かれています。
監督の芸術的感性を満たすような腕の出し方を見つける問題が NP 困難であることを示してください。
-
次のパーティでは招待客の一人が三チーム対戦マンブレッティーペグ (Three-Way Mumbletypeg) をやろうと提案するでしょう。これは三つのチームとナイフを使って遊ぶゲームであり、公式ルール (1652 年の聖ローマ三チーム対戦マンブレッティーペグ協議会で決定) は以下の通りです:
-
全てのチームには一人以上のメンバーが必要である。
-
同じチームの任意の二人は知り合いでなければならない。
-
試合を観戦する全ての人はいずれかのチームに所属しなければならない。
パーティの参加者の中にはお互いに知り合いでない人も含まれますが、パーティはもちろん楽しいものになるので、誰もパーティを離れたくはありません。パーティのホストはあなたのアルゴリズムの腕前が生かされたスリリングな話を聞きつけ、あなたに参加者の知り合い関係のリストを渡し、チームを作っておくように頼んできました。彼はその間にナイフを研いでおくとのことです。
パーティの参加者を三チーム対戦マンブレッティーペグのチームに分けることができるかを判定する多項式時間アルゴリズムを説明するか、この問題が NP 困難であることを示してください。
-
-
あなたが参加しているパーティはとても楽しく進んでいますが、ここでアルゴリズム行進の時間がやってきました。このダンスはコンビ漫才師いつもここからがピタゴラスイッチという日本の子供向けテレビ番組用に作成したものです。アルゴリズム行進では何人かの人が一列に並び、先頭の人から一テンポずつずれながら特定の動きをしていきます。この行進はダンスにおける輪唱あるいはカノンと言うことができます ("Row Row Row Your Boat" や "Frère Jacques" のような感じです)。
エチケット上、この行進をするときにはすぐ前にいる人と知り合いでなければなりません。もしそうしなかった場合には行進を間違えたときに知らない人同士がひどく恥ずかしい思いをしてしまうからです。パーティの参加者の誰と誰が知り合いかを記した完全なリストが与えられたとします。アルゴリズム行進に参加できる最大人数を求める問題が NP 困難であることを示してください。一般性を失うことなくパーティに忍者が参加しないことを仮定して構いません。
-
♣ 非決定性有限状態オートマトンと正規表現に関する次の問題が NP 困難であることを示してください。
-
アルファベット \(\Sigma = \lbrace {\color{maroon}{0}}, {\color{maroon}{1}} \rbrace\) 上の NFA \(M\) が与えられる。\(\Sigma^{\ast}\) に含まれる文字列で \(M\) が受理しないものは存在するか?
-
アルファベット \(\Sigma = \lbrace {\color{maroon}{0}}, {\color{maroon}{1}} \rbrace\) 上の非巡回 NFA \(M\) が与えられる。\(\Sigma^{\ast}\) に含まれる \(M\) が受理しない最短の文字列は何か?
-
アルファベット \(\Sigma = \lbrace {\color{maroon}{0}}, {\color{maroon}{1}} \rbrace\) 上の正規表現 \(R\) が与えられる。\(\Sigma^{\ast}\) に含まれる文字列で \(R\) とマッチしないものは存在するか?
-
アルファベット \(\Sigma = \lbrace {\color{maroon}{0}}, {\color{maroon}{1}} \rbrace\) 上のスターを含まない正規表現 \(R\) が与えられる。\(\Sigma^{\ast}\) に含まれる \(R\) とマッチしない文字列で最短のものは何か?
(実は (a) と (c) の問題は PSPACE 完全であり、PSPACE に属するという証明さえ自明ではありません)
-
-
♣
-
次の問題に対する多項式時間アルゴリズムを説明してください: 「アルファベット \(\Sigma = \lbrace {\color{maroon}{0}}, {\color{maroon}{1}} \rbrace\) 上の NFA \(M\) が与えられる。\(\Sigma^{\ast}\) に含まれる文字列で \(M\) が受理するものは存在するか?」
-
次の問題に対する多項式時間アルゴリズムを説明してください: 「アルファベット \(\Sigma = \lbrace {\color{maroon}{0}}, {\color{maroon}{1}} \rbrace\) 上の正規表現 \(R\) が与えられる。\(\Sigma^{\ast}\) に含まれる文字列で \(R\) とマッチするものは存在するか?」
-
任意の正規表現の否定もまた正規表現です。この問題で答えた二つのアルゴリズムと前問で示した NP 困難性をもって P=NP を結論できないのはどうしてですか?
-
-
Charon は最近死亡した \(n\) 人の人間の魂を Acheron 川を通って Hades まで船で送って行こうとしています。特定の乗客同士は不倶戴天の敵なので、Charon が一緒にいるときにしか同時に川の同じ岸にいることができません (その二人が一緒にいる状態で Charon が岸を離れると、二人はお互いの口に入った obols の取り合いを始め、彼らの魂は Acheron の岸を永遠に彷徨うことになってしまいます。つまり、とても悪いことが起こります)。船には Charon を含めて \(k\) 人が乗ることができ、船を操縦できるのは Charon だけです28。
Charon が \(n\) 人の魂を Acheron まで無事に送ることができるかどうかを判定する問題が NP 完全であることを示してください (無事と言いますが、死んでも構いません。元から死んでいるので)。Charon 問題の入力は整数 \(n, k\) と乗客の敵対関係を表す \(n\) 頂点のグラフ \(G\) であり、出力は \(\textsc{True}\) または \(\textsc{False}\) です。
答えを古典ラテン語で書くのはやめてください。
-
この意味の「効率的である」という概念は 1965 年に Alan Cobham (アラン・コブハム) によって、同じく 1965 年に Jack Edmonds (ジャック・エドモンズ) によって、1966 年に Michael Rabin (マイケル・レビン) によってそれぞれ独立に提唱されました。ただし、Kurt Gödel (クルト・ゲーデル)、John Nash (ジョン・ナッシュ)、John von Neumann (ジョン・フォン・ノイマン) も同じ概念についての考察を十年以上前に行っています。[return]
-
おそらく最も重要な進展は barrier result の形をとるものでしょう。この結果からは、ある条件を満たすどんな証明手段も失敗する運命にあるということが分かります。本当にそのままの意味で、P \(\neq\) NP をどうすれば証明できるかは誰にも分からないだけではなく、ある種の方法を使ったときにはどうやっても P \(\neq\) NP が証明できないことが証明されているのです![return]
-
Levin は自身の結果を 1971 年にモスクワで行われたセミナーで発表しており、そのときはまだ Ph.D. 生でした。Cook による証明の報は少なくとも 1973 年になるまでソ連に届かず、届いたのは Levin が自身の結果を発表した後のことでした。スティグラーの法則に従って、この結果は "Cook の定理" と呼ばれることが多いです。Levin は政治的理由によりモスクワ大学での Ph.D. を拒否され、1978 年にはアメリカに移住し、翌年 MIT で Ph.D. を取得しています。Cook は世界的な影響力を持つことになる論文を発表するわずか一年前の 1970 年にカリフォルニア大学バークレー校のテニュア職を断られています。Cook はこの証明によってチューリング賞を受賞しました (Levin は受賞しませんでした)。[return]
-
もし興味があるなら、http://algorithms.wtf にある非決定性チューリング機械に関する講義ノート、あるいは Boaz Barak による素晴らしいプロジェクト Introduction to Theoretical Computer Science を見てください[return]
-
ランダムアクセス機械 (random access machine, RAM) は物理的なコンピューターで行われる計算のより正確なモデルです。標準的なランダムアクセス機械は無限の配列 \(M[0..\infty]\) を持ち、\(M[i]\) には \(w\) ビットの整数が保持されます (\(w\) は固定された整数)。また任意のメモリアドレスに対する読み込みと書き込みは定数時間で行えます。正式な RAM アルゴリズムはアセンブリの言語を使って書かれ、\(\texttt{ADD } i,j,k\) (\(M[i] \leftarrow\) \(M[j] + M[k]\)) や \(\texttt{INDIR } i,j\) (\(M[i] \leftarrow \) \(M[M[j]]\)) や \(\texttt{IF0GOTO } i,l\) (もし \(M[i] = 0\) なら \(l\) 行に移動せよ) などの命令を持ちます。正確な命令セットは計算能力と驚くほど関係がありません。また全ての命令は単位時間で実行できると定義されます。算術演算の精度にさえ気を付ければ、RAM アルゴリズムは高レベルな疑似コードを使っても正確に書くことができます。[return]
-
売られている不動産のマスに止まったプレイヤーがその不動産を買うことを拒否した (あるいは買うだけの金が無い) 場合、不動産は競売にかけられる。最初に不動産を買うことを拒否したプレイヤーも競売に参加でき、競売の結果の値段は元の値段より高くも低くもなりうる。刑務所にいるプレイヤーも不動産、家、ホテルの売買および家賃の徴収を行ってよい。ゲームには 32 の家と 12 のホテルがある。それらが無くなったら、無くなる。特に全ての家が既にボード上にあるときにはホテルを 4 つの家にダウングレードさせることができず、取り壊すことしかできない。プレイヤーは未開発の不動産を他のプレイヤーと交換したり売ったりできるが、銀行に売り戻すことはできない。無料駐車場に止まったプレイヤーは何も得られない。Go に止まったプレイヤーはちょうど $200 を得る。鉄道は魔法の輸送機関でない。そして最後に、Jeff は必ず長靴を手に入れる。T-Rex でもペンギンでもなく ――長靴、クソッ。[return]
-
Kate Erickson, personal communication, 2011. 白黒のバージョンを読んでいる人へ: 丸くなっているものは虹です。[return]
-
各節のリテラルが最大でも三つであるような連言標準形 \(\Phi_{2}\) を使ってブール回路 \(K\) を表すためのこの方法は、1966 年に Grigorii Tseitin (グリゴリイ・セイティン) によって示されています。 1966 年というのは Levin が prebor problems に対する結果を公表する五年前です。同じ論文で Tseitin は、私たちが現在 \(\textsc{CNF-SAT}\) と呼ぶ問題をおそらく世界で初めて定義しています。[return]
-
1996 年のオフブロードウェイのショー Ricky Jay and his 52 Assistants より。[return]
-
例えば以前に示した \(\textsc{CircuitSAT}\) から \(\textsc{SAT}\) への帰着では各ゲートを論理式における節に変換しましたが、この帰着では節が "ゲートガジェット" となります。また \(\textsc{3SAT}\) から \(\textsc{MaxIndSet}\) への帰着では、節ガジェット (三角形) と変数ガジェット (矛盾する辺の間の辺) という二つのガジェットが登場しました。[return]
-
Michael Garey and David Johnson. Computers and Intractability: A Guide to the Theory of NP-Completeness. W. H. Freeman and Co., 1979. えぇ、この本は本当に真っ黒です。[return]
-
後にオフブロードウェイで Richard Karp and his 21 Assistants として上演され、Karp は当然
TonyTuring 賞を受賞しました。[return] -
以外にも、\(\textsc{PlanarNotAllEqual3SAT}\) は多項式時間で解けます![return]
-
Richard Kaye. Minesweeper is NP-complete. Mathematical Intelligencer 22(2):9–15, 2000. こちらも参照: Allan Scott, Ulrike Stege, and Iris van Rooij. Minesweeper may not be NP-complete but is hard nonetheless. Mathematical Intelligencer 33(4):5–17, 2011.[return]
-
Takayuki Yato and Takahiro Seta. Complexity and completeness of finding another solution and its application to puzzles. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences E86-A(5):1052–1060, 2003. http://www-imai.is.s.u-tokyo.ac.jp/~yato/data2/MasterThesis.pdf.[return]
-
Ron Breukelaar*, Erik D. Demaine, Susan Hohenberger*, Hendrik J. Hoogeboom, Walter A. Kosters, and David Liben-Nowell*. Tetris is hard, even to approximate. International Journal of Computational Geometry and Applications 14:41–68, 2004.[return]
-
Luc Longpré and Pierre McKenzie. The complexity of Solitaire. Proceedings of the 32nd International Mathematical Foundations of Computer Science, 182–193, 2007.[return]
-
Giovanni Viglietta. Gaming is a hard job, but someone has to do it! Theory of Computing Systems, 54(4):595–621, 2014. http://giovanniviglietta.com/papers/gaming2.pdf.[return]
-
Greg Aloupis, Erik D. Demaine, Alan Guo, and Giovanni Viglietta. Classic Nintendo games Are (computationally) hard. Theoretical Computer Science 586:135–160, 2015. http://arxiv.org/abs/1203.1895.[return]
-
Luciano Gualà, Stefano Leucci, Emanuele Natale. Bejeweled, Candy Crush and other match-three games are (NP-)hard. Proc. 2014 IEEE Conference on Computational Intelligence and Games, 2014. http://arxiv.org/abs/1403.5830.[return]
-
Further evidence for the "rule of three". Stefan Langerman and Yushi Uno. Threes!, Fives, 1024!, and 2048 are Hard. Proc. 8th International Conference on Fun with Algorithms, 2016. https://arxiv.org/abs/1505.04274.[return]
-
Erik D. Demaine, Sarah Eisenstat, and Mikhail Rudoy. Solving the Rubik's Cube optimally is NP-complete. Proc. 35th Symposium on Theoretical Aspects of Computer Science, 2018. https://arxiv.org/abs/1706.06708.[return]
-
Erik D. Demaine, Hiro Ito, Stefan Langerman, Jayson Lynch, Mikhail Rudoy, and Kai Xiao.Cookie Clicker. Preprint, August 2018. https://arxiv.org/abs/1808.07540.[return]
-
Theoretical Computer Science Stack Exchange より: http://cstheory.stackexchange.com/a/1999/111[return]
-
ゲームとパズルの計算複雑性に関する結果の優れた (しかし古くなりつつあるのも事実な) まとめについては、Erik Demaine と Bob Hearn による Games, Puzzles, and Computation を参照してください。[return]
-
整数はサイコロと同じように点の数で表されることが多いです。一般的なドミノでは点の数は 0 から 6 であり、大きくても 9 あるいは 12 まで書かれたものがある程度ですが、この問題では任意の大きさの整数が書かれているとします。またドミノは全ての整数の組が書かれたドミノをちょうど一つずつ含むことが普通ですが、この問題ではこのことを仮定しません。[return]
-
この問題はよく知られたオオカミ-ヒツジ-キャベツのパズルの一般化です。このパズルが登場する最古の例は歴史的価値の高い中世の写本 Propositiones ad Acuendos Juvenes (Problems to Sharpen the Young, 若者を磨くための問題集) です。
XVIII. Propositio De Homine et Capra et Lvpo.
Homo quidam debebat ultra fluuium transferre lupum, capram, et fasciculum cauli. Et non potuit aliam nauem inuenire, nisi quae duos tantum ex ipsis ferre ualebat. Praeceptum itaque ei fuerat, ut omnia haec ultra illaesa omnino transferret. Dicat, qui potest, quomodo eis illaesis transire potuit?
Solutio. Simili namque tenore ducerem prius capram et dimitterem foris lupum et caulum. Tum deinde uenirem, lupumque transferrem: lupoque foris misso capram naui receptam ultra reducerem; capramque foris missam caulum transueherem ultra; atque iterum remigassem, capramque assumptam ultra duxissem. Sicque faciendo facta erit remigatio salubris, absque uoragine lacerationis.
古典ラテン語は最近読んでいないのでちょっと、というごく少数の読者のために、翻訳もつけておきます:
XVIII. 男とヒツジとオオカミの問題
男はオオカミとヒツジとキャベツを川の向こう木まで送らなければならない。しかし、船が [一度に] 耐えられるのは [男を含めて] 二つ [の重さ] までである。可能ならば、その方法を答えよ: 全ての荷物を無事に向こう岸まで届けることができるか?
答え [前問と] 同じように、最初にヒツジを向こう岸まで連れて行き、こちら側の岸にオオカミとキャベツを残す。その後オオカミを向こう岸に連れて行き、そのとき向こう岸にいるヒツジをこちら側の岸に連れ帰る。その後ヒツジをこちら側の岸に置き、キャベツを向こう岸に持っていく。それからヒツジを連れて向こう岸に渡れば、全員が向こう岸に行くことができ、流血沙汰も起きない。
Propositiones の作者として最も有力視されているのは 8 世紀の英国人学者 Alcuin of York (ヨークのアルクィン) です。Alcuin がこの本の作者であることの証拠は若干状況証拠めいているのですが、彼がカール大帝とのやり取りの中で "算術に関する娯楽目的の問題" を送ったことは分かっています。現代の学者のほとんどは、たとえ Alcuin が本当に Propositiones を書いていたとしても、彼が全ての問題を考え着いたというわけではなく、さらに古い文献から集めてきたのだろうと考えています。
決して変わらないものもあるようです。[return]
