二部マッチング
もう一つのよく知られた最大フローの応用は、二部グラフの最大マッチング (maximum matching) の計算です。グラフのマッチングとは全ての頂点の次数が最大でも \(1\) であるような部分グラフのことであり、同じ頂点を共有しない辺の集合としても定義できます。ここで考える問題はマッチングであって辺の数が最大のものを計算する問題です。
例えば何人かの医師が職を探していて、いくつかの病院が医師を探しているとしましょう。各医師は働きたい病院をいくつか提示し、各病院は雇いたい医師を何人か提示しているときに、お互いが納得するような医師と病院の雇用関係をなるべく多く作りたいとします1。この問題は医師と病院を頂点とし、互いに雇用関係を結べる場合に限って辺があるような二部グラフに対する最大マッチングを求める問題と考えることができます。
この問題を最大フローへの帰着を使って解く方法をこれから示します。\(G\) を二部グラフとし、頂点集合は \(L \cup R\) であって、辺は \(L\) にある頂点と \(R\) にある頂点を結んでいるとします。このとき \(G\) から新しいグラフ \(\tilde{G}\) を次のように作成します:
- 全ての辺を \(L\) から \(R\) に向き付ける。
- 新しい頂点 \(s\) と \(t\) を追加する。
- \(s\) から \(L\) の全ての頂点への辺を追加する。
- \(t\) から \(R\) の全ての頂点への辺を追加する。
- 全ての辺の重みを \(1\) とする。
\(G\) の任意のマッチング \(M\) は次のようにして \(G^{\prime}\) のフロー \(f_{M}\) に変形できます: 「全ての \(M\) の辺 \(uw\) について、\(s \rightarrow u \rightarrow w \rightarrow t\) という辺に沿って \(1\) 単位のフローを追加する」 この処理によって追加される有向路は \(s\) と \(t\) 以外に点を共有しないので、各頂点における保存条件が満たされます。また \(f_{M}\) の値は \(M\) に含まれる辺の数と等しくなります。
逆にFord-Fulkerson の増加路アルゴリズムを使って計算した \(G^{\prime}\) の \((s,t)\)-フローを \(f\) とします。辺の容量が整数なことから Ford-Fulkerson のアルゴリズムが辺に割り当てるフローは必ず整数 (再帰法で簡単に示せます。ヒント、ヒント) であり、全ての辺が \(1\) 単位の容量を持つことから \(f\) は \(G^{\prime}\) の辺を飽和させる (\(f(e)=1\)) か避ける (\(f(e) = 0\)) かのどちらかです。さらに \(L\) の各頂点に入る辺の数および \(R\) の各頂点から出る辺の数は最大でも \(1\) なので、\(L\) から \(R\) への飽和した辺全体の集合は \(G\) のマッチングとなり、その大きさは \(|f|\) です。
以上より \(G\) の最大マッチングの大きさは \(G^{\prime}\) の最大フローの値と等しいこと、さらに増加路を使って作られた最大フローから \(O(E)\) 時間で最大マッチングを計算できることが分かります。よって Orlin のアルゴリズムあるいは単純に Ford-Fulkerson のアルゴリズムを使えば、二部グラフの最大マッチングを \(\pmb{O(VE)}\) 時間で計算できます。
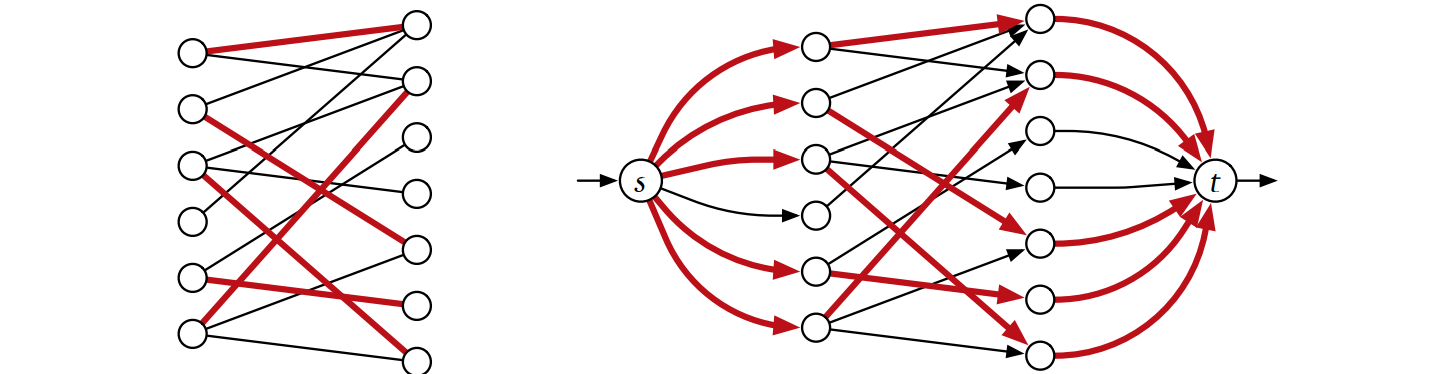
Ford-Fulkerson のアルゴリズムを \(G^{\prime}\) に対して実行したときの様子を元の二部グラフ \(G\) の視点で観察すると、面白いことが分かります。アルゴリズムは \(G\) におけるマッチング \(M\) を空のマッチングから初めて構成しますが、\(M\) における辺は \(G^{\prime}\) においてフローが流れている辺に対応します。\(M\) の辺に含まれる \(G\) の頂点をマッチしていると呼び、そうでない点をマッチしていないと呼ぶことにします。そうするとアルゴリズムの各反復で探索されるのは \(G\) における"交互路" ――\(L\) のマッチしていない点と \(R\) のマッチされていない点を結ぶ辺から始まり、以降は \(M\) に属する辺と \(M\) に属さない辺が続くような路―― であり、\(G\) における交互路が \(G^{\prime}\) における増加路に対応します。増加路 \(P\) が見つかったならば、\(M\) を \(P\) との対称差 \(M \otimes P\) で更新します。これによって \(M\) の大きさは一増え、一回の反復が終了します。もし増加路が無かった場合には、最大フロー最小カット定理から \(M\) が最大マッチングであることが分かるので、アルゴリズムは終了します。増加路を見つけるのには \(O(E)\) 時間かかり、反復は最大で \(V\) 回なので、このアルゴリズム全体の実行時間は \(\pmb{O(VE)}\) です。上図にアルゴリズムを実行した様子を示します。
最大二部マッチングの交互路を使った特徴付けは Claude Berge (クロード・ベルジュ) によって 1957 年に (最大フロー最小カット定理とは独立に) 初めて示されました。また似た手続きを含むアルゴリズムは 1955 年には Harold Kuhn (ハロルド・クーン) によって、1916 年には Dénes Kőnig (デニス・ケーニヒ) によって、1836 年には Carl Jacobi (カール・ヤコビ) によってそれぞれ示されています。
1973 年に John Hopcroft (ジョン・ホップクロフト) と Richard Karp (リチャード・カープ) によって提案されたより洗練されたアルゴリズムを使うと、二部グラフの最大マッチングを \(O(\sqrt{V}E)\) 時間で計算できます。このアルゴリズムは各反復で互いに交わらない交互路を複数見つけます。