木の上の動的計画法

今まで見てきた動的計画法の例はどれも、再帰的な小問題の答えを格納するのに多次元配列を使っていました。しかし次の例が示すように、配列が常に一番良いデータ構造であるとは限りません。

グラフの独立集合 (independent set) とは、頂点の部分集合であってどの頂点の間にも辺がないものを言います。任意のグラフの最大独立集合を見つけるのは極端に難しい問題であり、実際これは十二章で扱う NP 困難な問題の中でも有名なものです。しかしグラフがある特別なクラスに属している場合には、最大独立集合を高速に求めることができます。例えばグラフが \(n\) 個の頂点からなる木ならば、最大独立集合は次に説明する方法を使って \(O(n)\) 時間で求められます。

木 \(T\) が与えられたとします。このとき、一般性を失うことなく \(T\) が根付きの木である、つまり根と呼ばれる頂点があり、全ての辺が暗黙のうちに根から遠ざかる方向に方向付けされていると仮定できます (もし \(T\) が根無し木 ――連結非巡回無向グラフ―― ならば、任意の頂点を根とみなすことができます)。頂点 \(w\) から根への唯一の道に頂点 \(v\) が含まれるとき、\(w\) は \(v\) の子孫 (descendant) であると言います。同様に \(v\) の子孫 (descendants) とは \(v\) および \(v\) の子の子孫を合わせたものです。また \(T\) の頂点 \(v\) を根とする部分木とは、\(v\) の子孫とそれらを結ぶ辺からなる木です。

\(T\) の任意の頂点 \(v\) に対して、\(v\) を根とする部分木の最大独立集合を \(\mathit{MIS}(v)\) と書くことにします。 \(v\) を根とする部分木の独立集合で \(v\) を含まないものは、\(v\) の子を根とする部分木の独立集合の和集合です。また \(v\) を根とする部分木の独立集合で \(v\) を含むものには \(v\) の子が含まれず、\(v\) の孫を根とする部分木の独立集合の和集合に \(v\) を加えたものとなります。以上の観察から、\(\mathit{MIS}\) は次の再帰方程式に従います。ここで \(w \downarrow v\) という標準的でない記法は「\(w\) は \(v\) の子である」を意味します。 \[ \mathit{MIS}(v) = \max \left\lbrace \sum_{w \downarrow v} \mathit{MIS}(w), 1 + \sum_{w \downarrow v} \sum_{x \downarrow w} \mathit{MIS}(x) \right\rbrace \]

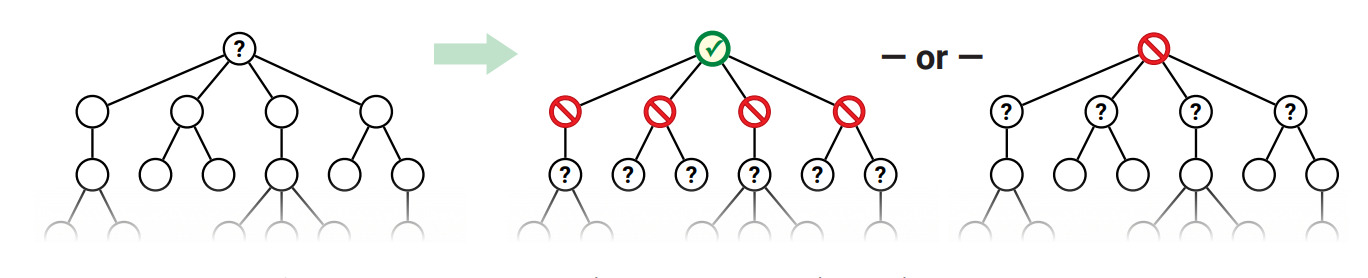
与えられた木 \(T\) の根 \(r\) について \(\mathit{MIS}(r)\) を計算することが目標となります。

この種類の再帰方程式をメモ化するときにはどのようなデータ構造を使うべきでしょうか？ 自然な選択肢は木 \(\pmb{T}\) そのものです！ つまり \(T\) の各頂点 \(v\) に対して、新しいフィールド \(v.\mathit{MIS}\) に \(\mathit{MIS}(v)\) を格納していくということです (理論上は木ではなく配列を使うこともできますが、頂点とそれに対応する配列の要素の間を行ったり来たりする必要があります。そんなことをする必要はないでしょう)。

小問題はどのような順番で考えればよいでしょうか？ 任意の頂点 \(v\) が依存する小問題は \(v\) の子と孫の小問題なので、全ての頂点がその親よりも前にくるのであればどんな順番でも使うことができます。ここではよく知られた帰りがけ順の走査を使います。

このアルゴリズムの実行時間はどれくらいでしょうか？ 頂点 \(v\) に対する小問題の再帰的でない部分の実行時間は \(v\) の子と孫の数に比例し、この数は頂点によって大きく変動するので評価が困難です。しかし、逆方向に考えると上手く行きます: 全ての頂点はその親と祖父母の小問題に対して実行時間を定数時間だけ上乗せします！ 各頂点の親と祖父母は多くても一つずつなので、アルゴリズム全体は \(\pmb{O(n)}\) 時間で実行されます。

完成したアルゴリズムを次に示します。このアルゴリズムは再帰的ですが、それは木に対する帰りがけ順の走査を実装するのに再帰を使っているからであって、動的計画法を使っていないからではありません。

\(T\) の頂点 \(v\) に対する二つの関数を次のように定義すると、さらに単純な線形時間アルゴリズムが得られます。

• \(\mathit{\mathit{MISyes}}(v)\) を、\(v\) を根とする部分木の \(v\) を含む独立集合の最大サイズとする。
• \(\mathit{\mathit{MISno}}(v)\) を、\(v\) を根とする部分木の \(v\) を含まない独立集合の最大サイズとする。

ここで計算すべきは \(T\) の根 \(r\) に対する \(\max\lbrace \mathit{\mathit{MISyes}}(r), \mathit{\mathit{MISno}}(r) \rbrace\) の値です。二つの関数は次の相互再帰方程式を満たします: \[ \begin{aligned} \mathit{\mathit{MISyes}}(v) & = 1 + \sum_{w \downarrow v} \mathit{\mathit{MISno}}(w) \\ \mathit{\mathit{MISno}}(v) & = \sum_{w \downarrow v} \max\lbrace \mathit{\mathit{MISyes}}(w), \mathit{\mathit{MISno}}(w) \rbrace \end{aligned} \] ここでも、関数の値を \(T\) と同じ形の木に格納します。関数が二つあるので、各頂点に作成される新しいフィールドは二つです。木に対する帰りがけ順の走査を使えば、全ての頂点に対する二つの関数の値を \(\pmb{O(n)}\) 時間で計算できます。次に示すアルゴリズムは \(v\) における二つの関数の値を記録するだけではなく、その二つのうちで大きい方を返します。

ループの二行目の \(\mathit{w.\mathit{MISno}}\) は一つ前の行の \(MIS(w)\) の呼び出しの中で記録された値です。