最短路木

ある頂点から別の頂点への最短路を計算するほとんど全てのアルゴリズムが実際に解いているのは、次に説明する単一ソース最短路 (single source shortest path, SSSP) 問題です。これは \(s\) からグラフに含まれる他の全ての頂点への最短路を求める問題であり、通常は \(s\) を根とする最短路木 (shortest path tree) を見つけることで解かれます。最短路木には求めるべき全ての最短路が含まれます。

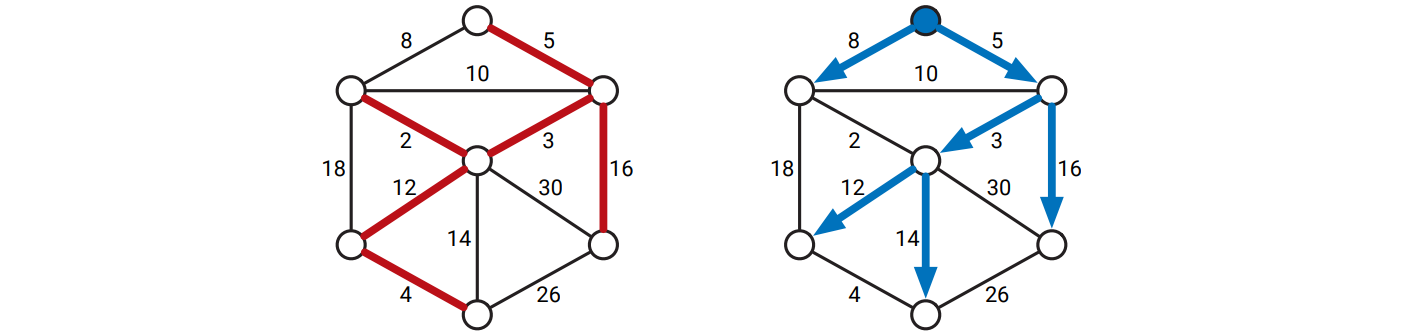
各頂点への最短路がユニークならばそれらの最短路を合わせると木になるというのはすぐに分かります。このような場合には、最短路の任意の部分路もまた最短路となるためです。またいずれかの頂点に対する最短路が複数ある場合でも、全ての頂点への最短路の和集合が木になるように各頂点への最短路を必ず選ぶことできます。つまり、もし \(s\) から \(u\) への最短路と \(s\) から \(v\) への最短路が最初の部分で一致していて、途中で離れ、最後にまた一致するようになっている場合には、路を改変することで二つの最短路が一度だけ一致するようにできます。

最短路木と最小全域木は両方ともある意味で最適な全域木ですが、全く異なる代物です。最短路木は根を持ち有向ですが、最小全域木は根を持たず無向です。最短路木は有向グラフに対して最も自然に定義されますが、最小全域木は無向グラフに対して最も自然に定義されます。辺の重みが全て異なるなら最小全域木は一つだけ存在しますが、最短路木はソース頂点を変えると変化します。さらに言えば、全ての頂点に対する最短路木が最小全域木と異なる辺を使うことだってあり得ます。

負辺

ほとんどの最短路問題では辺の重みが長さや距離や時間を表すので、辺の重みが非負、あるいは正であると仮定するのが自然です。しかし負辺を仮定した方が自然な最短路木アルゴリズムの応用もあります。例えば辺の重みがある頂点から別の頂点に移動するときのコストを表している場合、負の重みを持つ辺は負のコストを持った移動、つまり利益が生じる移動を表すので、それほど不自然でもありません。

負辺は多くの最短路問題において悩みの種です。なぜなら負閉路があると最短路が存在しないことがあるからです。正確に言うと、\(s\) から \(t\) への最短路が存在するのは \(s\) から \(t\) への路があって、かつ \(s\) から \(t\) へのどの路も負閉路に触れないときであり、かつそのときに限ります。負閉路に触れる \(s\) から \(t\) への任意の路について、閉路をもう一度多く回る路は必ず元の路より短くなる¹ため、\(s\) から \(t\) への路で負閉路に触れるものが一つでもあるなら \(s\) から \(t\) への最短路は存在しません。

負辺を持つグラフも考えたいので、この章で明示的に考えるのは有向グラフだけです。この章で説明される全てのアルゴリズムは無向グラフにも適用できますが、上手く行くのは負の重みを持つ辺が無いときだけです。無向グラフにおける負辺の正しい取り扱いは有向グラフの場合よりもはるかに難しくなります。例えば単純に無向グラフの辺を有向辺の組にすると、負辺が二つの辺からなる負閉路を作ってしまうので上手く行きません。また負辺を含む無向最短路の部分路は最短路であるとは限らず、したがって最短路がユニークであったとしても、一つのソース頂点から他の全ての頂点に対する最短路の和集合が木とならない場合があります。

負辺を持つ無向グラフの完全な取り扱いはこの本の範囲を超えます。Google を使ってさらに学びたい人のために言っておくと、負辺を持つ無向グラフの一つの最短路は \(O(VE + V^{2} \log V)\) 時間で計算でき、最大重みマッチングへの帰着を使います。

1. 正確に言えばここで議論しているのは最短路 (shortest path) ではなくて最短歩道 (shortest walk) です。しかしこの用語の乱用は通例となっています。用語を正確に使って議論すると、\(s\) が \(t\) に到達できるなら、\(s\) から \(t\) への最短単純路が存在します。ただ計算するのは (負閉路がある場合には、ハミルトン路問題からの簡単な帰着によって) NP 困難です。一方で、\(s\) から \(t\) への最短歩道が存在するならば、その歩道は単純路であり、もちろん \(s\) から \(t\) への最短の単純路です。ああややこしい。^[return]