素路被覆

有向グラフ \(G\) の路被覆 (path cover) とは、\(G\) の有向路の集合であって \(G\) の全ての辺が少なくとも一つの路に含まれるものを言います。\(G\) の素路被覆 (disjoint-path cover) とは、\(G\) の路被覆であってどの頂点もちょうど一つの路に含まれるものを言います。

任意の有向グラフには長さがゼロの路だけからなる自明な素路被覆がありますが、これは面白くありません。そうではなくて、なるべく少ない路を使った素路被覆を見つける問題を考えましょう。この問題は一般的なグラフに対しては NP 困難です ――有向グラフが大きさが \(1\) の素路被覆を持つことはハミルトン路を持つことと同値だからです―― が、有向非巡回グラフに対してはフローを使った効率の良いアルゴリズムが存在します。

与えられた有向非巡回グラフ \(G=(V,E)\) の最小素路被覆を求めるには、次に示す新しい二部グラフ \(G^{\prime} = (V^{\prime}, E^{\prime})\) を使います:

\(G\) の各頂点 \(v\) に対して、\(G^{\prime}\) には \(v^{\flat}\) と \(v^{\sharp}\) という頂点がある。
\(G\) の各有向辺 \(u \rightarrow v\) に対して、\(G^{\prime}\) には \(u^{\flat}v^{\#}\) という無向辺がある。

(\(G\) が隣接行列で表されているなら、\(G^{\prime}\) は同じ隣接行列で表される二部グラフです！)

図 11.5

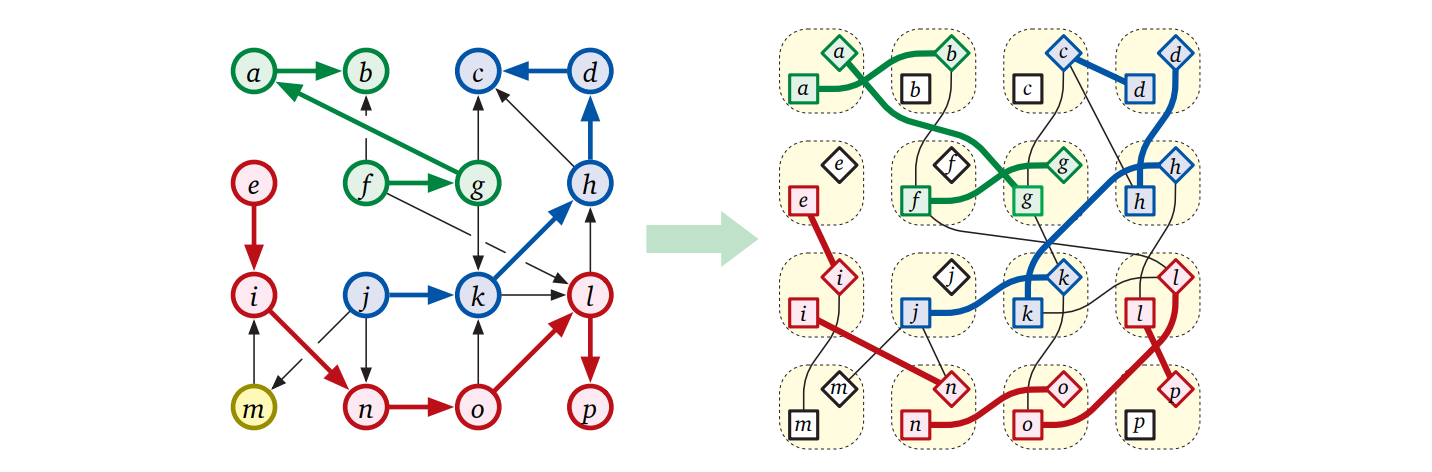
DAG の最小素路被覆を最大二部マッチングに帰着させる (四角がフラット \(\flat\)、ダイアモンド型がシャープ \(\sharp\) を表す)

「\(k\) 個の互いに素な路で \(G\) を被覆できる」が「\(G^{\prime}\) に大きさ \(V-k\) のマッチングが存在する」と同値なことをこれから示します。いつも通り、同値性は二つのステージに分けて示します。

\((\Rightarrow)\) \(G\) が \(k\) 個の互いに素な路からなる被覆 \(P\) を持つとする。\(P\) を部分グラフとみなすと、\(P\) の各頂点の入次数は \(0\) か \(1\) であり、入次数が \(0\) である点は \(P\) に含まれる路につき一つずつしか含まれない。よって \(P\) に含まれる辺の数は \(V - k\) 個である。\(G^{\prime}\) の辺の部分集合 \(M\) を次のように定義する: \[ M := \lbrace u^{\flat} v^{\sharp} \in E^{\prime}\ |\ u \rightarrow v \in P \rbrace \] \(P\) が素路被覆であることから、\(G\) の各頂点 \(v\) について \(v\) から出る辺と \(v\) に入る辺はどちらも最大一つであることが分かる。したがって \(G^{\prime}\) の各頂点は \(M\) において次数が \(1\) 以下であり、\(M\) は大きさ \(V - k\) のマッチングである。
\((\Leftarrow)\) \(G^{\prime}\) が大きさ \(V - k\) のマッチング \(M\) を持つとする。 \[ M^{\prime} := \lbrace u \rightarrow v \in E \ |\ u^{\flat}v^{\sharp} \in M \rbrace \] とし、\(P = (V, M^{\prime})\) と置くことで \(M\) を \(G\) の部分グラフに変換する。マッチングの定義から、\(G\) の各頂点は \(P\) において外向き辺および内向き辺をそれぞれ最大でも一つしか持たない。よって \(P\) は \(G\) の互いに素な有向路の集合であり、\(P\) が全ての頂点を含むことからこの集合は \(V-k\) 個の辺を持つ素路被覆である。\(P\) に含まれる路の数は \(M^{\prime}\) において向かってくる辺が存在しない \(G\) の頂点の数と等しいので、\(P\) にはちょうど \(k\) 個の路が含まれることが分かる。

以上より \(G\) の最小素路被覆を \(G^{\prime}\) の最大マッチングを計算することで求められることが直ちに分かります。Ford-Fulkerson の最大フローアルゴリズムを使えば、この計算は \(O(V^{\prime} E^{\prime}) =\) \(\pmb{O(VE)}\) 時間で行えます。

この問題は DAG と路という言葉を使って定式化されていますが、実際には最大マッチングの問題です。つまり、グラフのなるべく多い頂点を (路における) 後者とマッチさせる問題であるということです。DAG を被覆するために必要な路の数は、前者を持たない頂点の数と同じになります (そしてもちろん、二部グラフの最大マッチング問題は実際には最大フローの問題です)。

教師の最小雇用問題

Sham-PooBanana 大学に戻って、"現実世界" のスケジューリング問題をもう一つ見ましょう¹。SPU では毎日数千の講義が開かれているのですが、予算の大幅な削減によって学部のサイズを大きく減らす必要が生じました。しかし生徒は既に学費を払っているために (そして大学には弁護士を雇うお金もないために)、講義カタログに載っている講義を全て開講できるだけの教授を残しておかなければなりません。残しておかなくてはいけない SPU の教授は最低で何人でしょうか？

残された学部の教授には曜日ごとに講義が割り当てられます。各教授に割り当てられる講義の時間は重なってはならず、さらに講義と講義の間には教室を移動するための空き時間が必要になります。問題を簡単にするために、全ての教授は全ての講義を教えることができ、さらにオフィスアワーも昼食休憩もトイレ休憩も取らないとしましょう²。

きちんと述べると、\(n\) 個の講義が \(m\) 箇所で開講されるときの問題の入力は次のデータです:

講義を表す配列 \(C[1..n]\): \(C[i]\) には三つのフィールドがあり、それぞれ開始時間 \(C[i].\mathit{start}\) と終了時間 \(C[i].\mathit{end}\) と教室の場所 \(C[i].\mathit{loc}\) である。
二次元配列 \(T[1..m, 1..m]\): \(T[u,v]\) が教室 \(u\) から教室 \(v\) へ移動するのにかかる時間を表す。

計算するのは全ての講義を開講するために必要な教授の数の最小値です。各教授に \(C[i]\) と \(c[j]\) が割り当てられ \(C[j].\mathit{start} \geq C[i].\mathit{start}\) であるとすれば、 \[ C[j].\mathit{start} \geq C[i].\mathit{end} + T[C[i].\mathit{loc}, C[j].\mathit{loc}] \] が満たされる必要があります。

この問題は素路被覆への帰着を使って解くことができます。素路被覆問題への入力は DAG \(G=(V,E)\) であり、\(G\) の頂点が講義を表し、二つの講義の間に辺があるのは時間帯が十分離れているために同じ教授が両方を担当できるときであるようなグラフとします。つまり有向辺 \(i \rightarrow j\) は同じ教授が講義 \(i\) と講義 \(j\) の両方を担当できることを示すということです。総当たりを使えばこのグラフを \(O(n^{2})\) 時間で簡単に構築できます。

\(G\) の素路被覆を前述のマッチングアルゴリズムを使って計算すれば、被覆に含まれる \(G\) の有向路がある一人の教授に対する講義スケジュールを表します。アルゴリズム全体の実行時間は \(O(n^{2} + VE) = \pmb{O(n^{3})}\) です³。

問題文では区間と距離という言葉が使われていたこの問題は、実際には最大マッチングの問題 (したがって最大フローの問題) であることが分かりました。つまり、できるだけ多くの講義を、同じ教授が担当する次の講義とマッチさせる問題であるということです。必要となる教授の数は次の講義が存在しない講義の数と等しくなります: そのような講義はある教授が担当する最後の講義です。

この問題のもう少し現実的な (気分が落ち込むこともない) 例としては、教授と講義の部分を飛行機とフライト、あるいはバスと運行ルートなどに変えたものを考えてください。^[return]
ただし生徒からのメールには教室を移動している間に返信できるとします。^[return]
全ての \(u, v\) について \(T[u,v]\) が同じだとした場合、スケジューリング問題は貪欲アルゴリズムを使って \(O(n \log n)\) 時間で解けます (多くのアメリカの大学では講義の間の休み時間が 10 分であり、これは普通の人間がキャンパス内の任意の教室からキャンパス内の任意の教室へと 10 分以内に移動できるという興味深い仮定に基づいています。この仮定が現実的だと思うなら、私の大学のキャンパスに来て二つの Siebel Center の間を歩いてみることをお勧めします)。^[return]