プロジェクト選択

最後の例として、与えられた $n$ 個のプロジェクトの中から実際に行うものを選択する問題を考えます。いくつかのプロジェクトは他のプロジェクトが終わるまで開始できず、その依存関係が有向非巡回グラフ $G$ で表されているとします。

$G$ の頂点はプロジェクトを表し、辺 $u \rightarrow v$ はプロジェクト $v$ が完了するまでプロジェクト $u$ に取り掛かれないことを表します (6.4 節で考えた依存グラフと同じ形式です)。そして各プロジェクトには完了したときに入手できる利益 $\$(v)$ が設定されており、負の利益を持つ (正のコストがかかる) プロジェクトも存在します。あなたが選ぶことができるのはプロジェクト集合の部分集合 $X$ であって、$X$ に含まれる任意のプロジェクトが依存するプロジェクトもまた $X$ に含まれるという条件を満たすものです。条件を満たすプロジェクトの部分集合であって利益の合計を最大化するものを見つけるのが目標です。例えば全てのプロジェクトに負の利益が設定されているなら、何も選ばないことを表す空集合が答になります。

図 11.6

8 個のプロジェクトからなる依存グラフ (ダイアモンド型の頂点が利益をもたらすプロジェクトを、四角の頂点がコストのかかるプロジェクトを表す。辺 $u \rightarrow v$ は $u$ が $v$ に依存することを示す)

抽象的に考えると、この問題の答えはプロジェクトの集合の二つの部分集合への分解、つまり選択するプロジェクトの集合 $S$ と選択しないプロジェクトの集合 $T$ への分解と捉えることができます。そのため、何らかのグラフにおける最小カットとしてこの問題をモデル化すれば良いのではないかという気がします。でもどんなグラフでしょう？依存関係を表現するにはどうすれば？ここで行いたいのは利益の最大化ですが、私たちが求められるのは最小カットだけです。どうすれば？負の利益を正の容量に変換するにはどうすればいいのでしょうか？

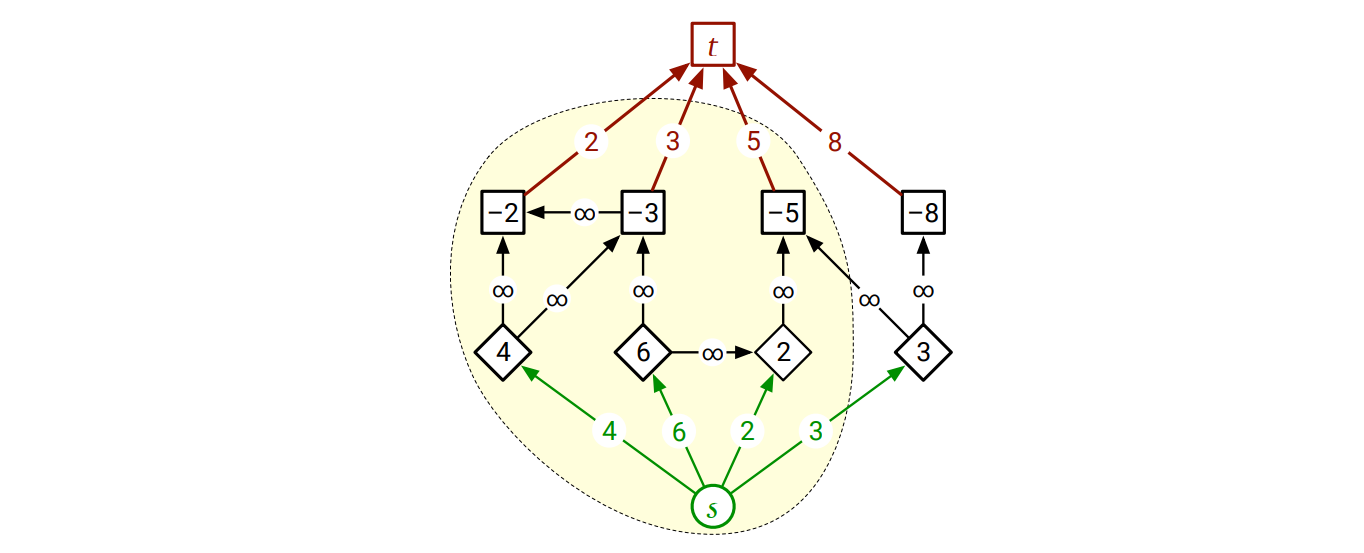
与えられた制約グラフ $G$ をフローネットワーク $G^{\prime}$ に変換するために、$G$ にソース頂点 $s$ とシンク頂点 $t$ を追加し、利益の出る ($\$ (v) > 0$ である) プロジェクト $v$ に対して辺 $s \rightarrow v$ を追加し、コストのかかる ($\$ (u) < 0$ である) プロジェクト $u$ に対して辺 $u \rightarrow t$ を追加します。$G^{\prime}$ の辺の容量は次のようにします:

利益の出るプロジェクト $v$ については $c(s \rightarrow v) = \$ (v)$
コストのかかるプロジェクト $u$ については $c(u \rightarrow t) = -\$ (u)$
その他の依存関係を表す辺 $u \rightarrow v$ について $c(u \rightarrow v) = \infty$

こうすれば辺の容量が正となるので、$G^{\prime}$ は最小カット問題の正しい入力となります。

$G^{\prime}$ における任意の $(s,t)$-カット $(s, t)$ を考えます。元の依存グラフ $G$ にあった辺 $u \rightarrow v$ に対して $u \in S$ かつ $v \in T$ なものが存在するなら $\|S, T\| = \infty$ です。したがって、カット $(s, t)$ の容量が有限のときに限って $S$ が実行可能なプロジェクトの集合としての条件を満たすということが言えます。

図 11.7

例の依存グラフに対するフローネットワークと容量 $13$ の最小カット。$P = 15$ なので、このカットによって選択されるプロジェクト全体の利益は $2$ である。

$G^{\prime}$ における小さい容量のカットが高い利益を持つプロジェクトの集合に対応することをこれから示します。具体的には、プロジェクトの集合として $S$ を選ぶと利益が $P - \|S,T\|$ となることを示します。ここで $P$ は正の利益の和です: \[ P = \sum_{v} \max \lbrace 0, \$ (v) \rbrace = \sum_{\$(v) > 0} \$(v) \] 証明は定義を追っていくだけで済みます。任意のプロジェクトの集合 $X$ について、次の三つの値を定義します: \[ \begin{aligned} \mathit{cost}(X) & := \sum_{u \in X, \$(u) < 0} - \$ (u) = \sum_{u \in X} c(u \rightarrow t) \\ \mathit{yeild}(X) & := \sum_{v \in X, \$(v) > 0} \$ (u) = \sum_{v \in X} c(s \rightarrow v) \\ \mathit{profit}(X) & := \sum_{v \in X} \$(v) = \mathit{yeild} (X) - \mathit{cost}(X) \end{aligned} \] (存在しない辺 $u \rightarrow v$ については $c(u \rightarrow v) = 0$ とします) 定義より $P = \mathit{yeild}(V) = \mathit{yeild}(S) + \mathit{yeild}(T)$ です。カット $(S, T)$ は有限の容量を持つので、$S$ と $T$ を結ぶ辺は $s \rightarrow v$ または $u \rightarrow t$ という形をしています。また $G^{\prime}$ の構成より辺 $s \rightarrow v$ について $v$ は利益をもたらすプロジェクトであり、辺 $u \rightarrow t$ について $t$ はコストのかかるプロジェクトです。よって $\|S, T\| = \mathit{cost}(S) + \mathit{yeild}(T)$ であり、直ちに $P - \|S,T\| =$ $\mathit{yeild} (S) - \mathit{cost}(S) =$ $\mathit{profit}(S)$ となって目当ての式が得られます。

よって $G^{\prime}$ の最小カットを求めることで全体の利益を最大化できます。$G$ からは $O(V+E)$ 時間で $G^{\prime}$ を構築でき、$G^{\prime}$ の最小 $(s,t)$-カットは Orlin のアルゴリズムを使えば $O(VE)$ 時間で計算できるので、プロジェクト選択のアルゴリズム全体の実行時間は $\pmb{O(VE)}$ です。