頂点容量と頂点素路

入力グラフ \(G\) が辺だけではなく頂点にも容量を持つとします。この設定では関数 \(f: E \rightarrow \mathbb{R}_{\geq 0}\) がフローであるための条件に新しい制約が加わります。その制約とは、\(s, t\) 以外の全ての頂点 \(v\) について \(v\) に入るフローの和が非負の定数 \(c(v)\) 以下でなければならないというものです (保存条件からこの値は \(v\) から出るフローの和と等しくなります): \[ \sum_{u \rightarrow v} f(u \rightarrow v) \leq c(v) \] この新しい制約があったとしても最大フローを計算できるでしょうか？

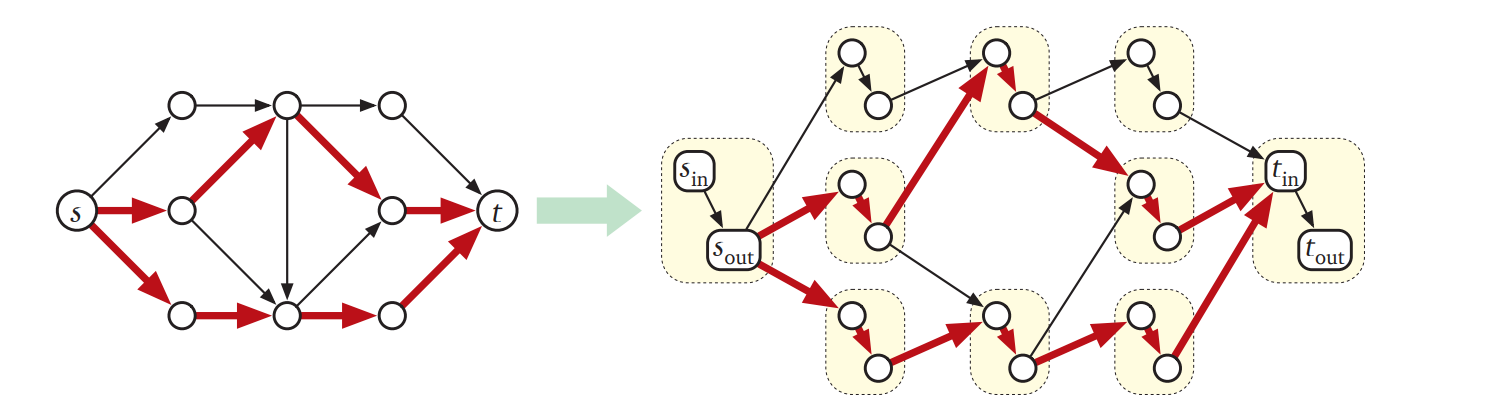
Ford と Fulkerson は 1962 年、この問題を辺だけに容量を持ったグラフ \(\tilde{G}\) に帰着させる方法を示しました。ここで \(\tilde{G}\) の頂点は \(G\) の頂点 \(v\) を \(v_{\text{in}}\) と \(v_{\text{out}}\) に分けた頂点であり、\(\tilde{G}\) の辺は全ての \(G\) の頂点 \(v\) に対する \(v_{\text{in}}\) から \(v_{\text{out}}\) への容量 \(c(v)\) の辺と全ての \(G\) の辺 \(u \rightarrow v\) に対する容量 \(c(u \rightarrow v)\) の \(u_{\text{out}} \rightarrow v_{\text{in}}\) という辺です。いつも通り定義を追っていくと、\(\tilde{G}\) における任意の実現可能な \((s_{\text{out}}, t_{\text{in}})\)-フローに対応する \(G\) の実現可能な \((s,t)\)-フローが存在し、両者は同じ値を持つことが分かります。つまり、\(\tilde{G}\) の最大フローが \(G\) の最大フローに対応します。

\(G\) から \(\tilde{G}\) への帰着には \(O(E)\) 時間かかり、その後の \(\tilde{G}\) の最大フローの計算には Orlin のアルゴリズムが使えるので、アルゴリズム全体の実行時間は \(\pmb{O(VE)}\) です。

ここまでくれば \(s\) から \(t\) への頂点素路集合の大きさの最大値を求めるのは簡単です: 全ての頂点に \(1\) の容量を割り当てて、そのグラフの最大フローを計算すれば良いのです！