ゲーム木

正方形のマス目からなる \(n \times n\) の格子を使った次の単純な二人対戦ゲームを考えます¹。このゲームは二人のプレイヤー Horace Fahlberg-Remsen (ホレース・ファールベルグ・レムセン) と Vera Rebaudi (ベラ・レバウディ)²が \(n\) 個の駒を盤の反対側に向かって移動させるゲームです。Horace の駒は左端の列に一列に並んだ状態でスタートし、水平方向に (horizontally) 右へ移動します。同じように Vera の駒は一番上の行に一列に並んだ状態からスタートし、一番下の列を目指して垂直に (vertically) 移動します。Horace は各ターンで二つの操作のうち一つを行うことができます。つまり、ある駒を一つ右の空のマスに移動させる move か、ある駒を Vera の駒をちょうど一つ飛び越して二つ隣の空のマスに移動させる jump です。全ての駒が move も jump もできない場合 Horace はパスとなります。同様に Vera は駒を一つ選んで下方向に move か jump を行うことができ、そのような操作ができなければパスです。最初に全ての駒を反対側まで移動させたプレイヤーの勝ちです (駒が盤の上にある限りプレイヤーのどちらかは合法的な手を打ち続けることができ、最終的に必ずどちらかのプレイヤーが勝つことを示すのは難しくありません) 。

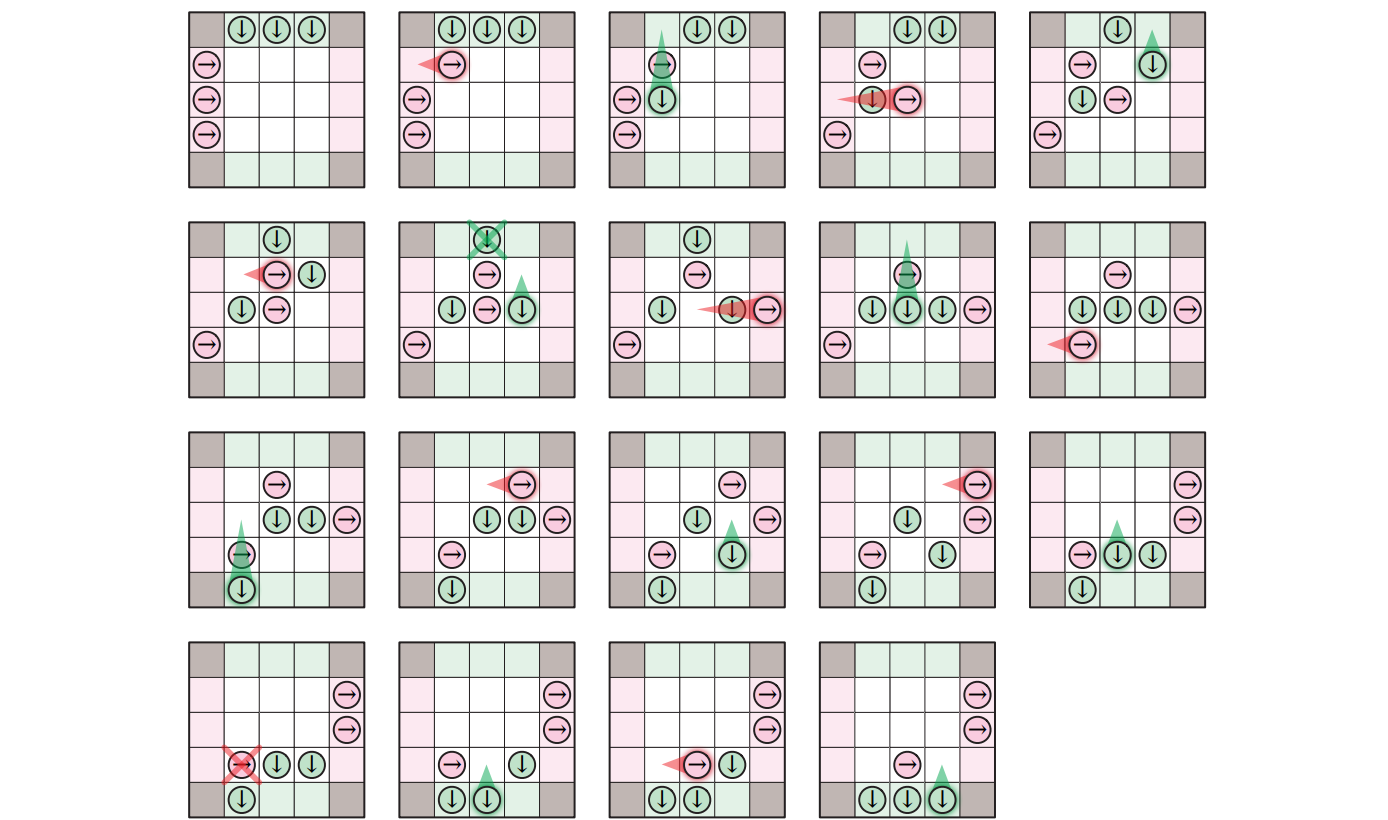
このゲームを過去に見たことがない限り³、どうすればこのゲームをうまくプレイできるか分からないでしょう。しかしこうして紹介しているのですから、もちろん、このゲームには完璧なプレイをする比較的単純なバックトラッキングを使ったアルゴリズムが存在します。つまり、完璧なプレイヤーとのゲームに途中から参加参加したときに、どうやって勝つかを (勝つことが可能ならば) 教えてくれるアルゴリズムがあるということです ――同様の戦術はランダム性がなく隠された情報がない任意の二人対戦ゲームに対して存在します。

ゲームの状態 (state) とは駒の位置と現在プレイヤーがどちらであるかという情報です。状態 \(x\) から状態 \(y\) に遷移できる場合に限って二つの状態を結ぶようにすると、ゲーム木 (game tree) ができます。この木の根はゲームの初期状態であり、根から葉への道は起こりうるゲームの展開の一つを表します。

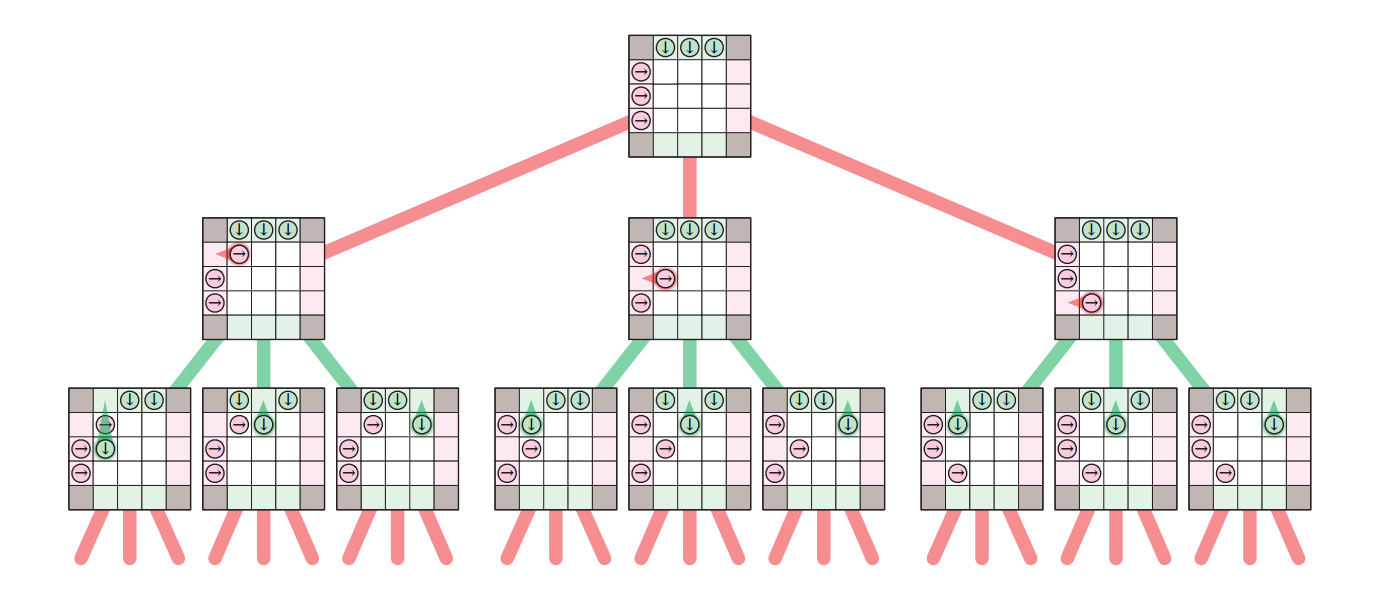
このゲーム木を理解しやすくするために、良い (good) 状態と悪い (bad) 状態を次のように定義します:

• 良いゲーム状態とは、現在のプレイヤーが勝っているか、相手が悪い状態になるような手を現在のプレイヤーが打てる状態。
• 悪いゲーム状態とは、現在のプレイヤーが負けているか、どんな手を打っても相手が良い状態になる状態。

言い換えると、ゲーム木の葉でない頂点が良いとはその子の少なくとも一つが悪いことであり、葉でない頂点が悪いとはその子の全てが良いことです。帰納法によって、良い状態にあるプレイヤーは相手が完璧にプレイしたとしてもゲームに勝利できることが示せます。反対に、悪い状態にあるプレイヤーは相手がミスをしない限り勝利できません。この再帰的な定義は 1913 年に Ernst Zermelo (エルンスト・ツェルメロ) によって初めて提案されました⁴。

この再帰的な定義を使うと、与えられた状態が良いか悪いかを判定する次のバックトラッキングを使ったアルゴリズムをすぐに得ます。本質的には、このアルゴリズムが行うのはゲーム木の深さ優先探索であり、このアルゴリズムの再帰木はゲーム木そのものです。このアルゴリズムを少し変更すれば良い手 (あるいは全ての良い手) を入力の状態に対して出力するようにできます。

ゲームをプレイするどんなアルゴリズムも、突き詰めればこのバックトラッキングを使った戦略に基づいています。しかしたいていのゲームでは状態の数が膨大になるので、ゲーム木全体を走査するのは現実的ではありません。そのためゲームのプログラムではヒューリスティック⁵を使ってゲーム木の刈り取りを行います。例えば、明らかに (あるいは"明らかに") 良い/悪い状態や、他の状態よりも良い/悪い状態を無視したり、葉を評価するもっと効率的なヒューリスティックを使って木の走査を途中で打ち切ったりします。

1. このゲームが何と呼ばれているか、および私が覚えているルールが正しいかどうかは分かりません。このゲーム (あるいはこのゲームに似たもの) は Lenny Pitt に教わりました。彼はレストランにおいてある人工甘味料の袋 (fake-sugar packet) でこのゲームをやることを勧めていました。^[return]

2. Constantin Fahlberg (コンスタンティン・ファールベルク) と Ira Remsen (アイラ・レムセン) は 1878 年に世界で初めてサッカリンを合成しました。このとき Fahlberg はコールタールの誘導体について研究する Remsen の研究室のポスドクでした。1900 年、Ovidio Rebaudi (オヴィディオ・レバウディ) は ka'a he'ê という植物についての世界で初めての化学的な解析を発表しました。この植物はグアラニー族で 1500 年以上にわたって栽培されてきた薬草で、現在ではステビア (Stevia rebaudiana) という名前で知られています。^[return]

3. もしあるなら、どこで知ったのかぜひ教えてください！^[return]

4. Zermelo が考えたゲームのクラスは有限の状態を持ちますが、手の列が無限に伸びることを許していたので、ここに示したものよりもう少し複雑です (Zermelo は無限に続くゲームを引き分けと定義しました)。^[return]

5. ヒューリスティックとは正しく動かないアルゴリズムのことを言います (ただし実用上はうまく動きます。たまに、見かけ上は)。^[return]