最長増加部分列 テイク 2
最長増加部分列を見つけるのに使えるバックトラッキングを使ったアルゴリズムはこれだけではありません。入力配列を一つずつ走査していくのではなくて、出力配列を一つずつ構築していくこともできます。つまり、「\(A[i]\) は出力配列に含まれるか?」ではなく「出力配列における次の要素は何か? そもそも存在するか?」を直接考えるということです。
この戦略を処理している途中に放り込まれた場合、次のような図を目にすることになります。黒いバーのすぐ左にある \(6\) がちょうど出力配列に入れられた要素であり、黒いバーより右にある要素のうちどれを次に出力配列に含まれるかをこれから決断することになります。
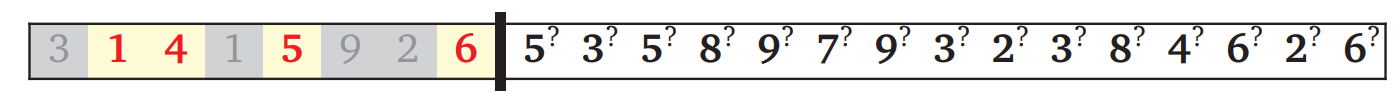
もちろん、バーより右にある数のうち \(6\) より大きいものだけを考えます。

これらの数字のうちどれを選べば良いか、私たちには何の手掛かりもありません。どの値が一番良いかを "賢く" 考えても話がこんがらがるだけなので、全ての選択肢を総当たりで試すことにします。それぞれの選択肢について、同じプロセスを再帰的に繰り返します:
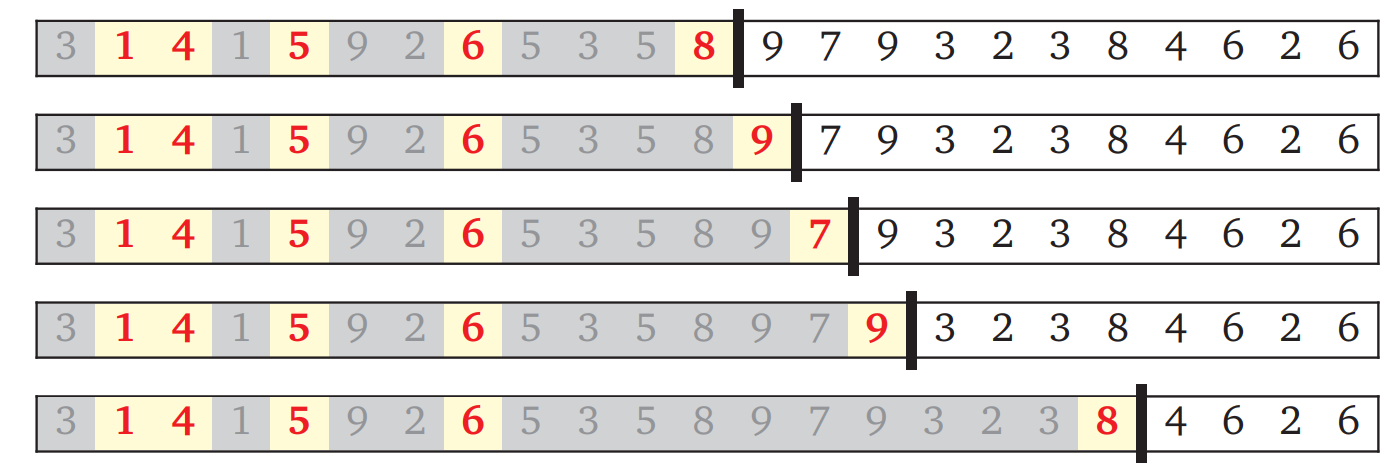
出力配列に次に入れる数の選択肢は、出力配列に最後に入れた数だけに依存します。そのため先ほどの図は処理が終わった部分を取り除いて単純化できます:
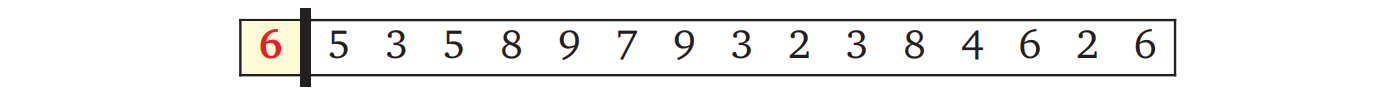
黒いバーの右側に残った数字は入力配列の接尾部分です。そのため、入力配列 \(A[1..n]\) をグローバル変数とすれば、再帰的な問題を添え字を使って次のように表せます:
添え字 \(i\) が与えられたときに、 \(A[i]\) で始まる \(A[i..n]\) の部分列の中で 最長のものを求めよ。
\(A[i]\) で始まる \(A[i..n]\) の部分列の中で一番長いものを \(\mathit{LISFirst}(i)\) と表すことにすると、上述のバックトラッキングを使った再帰的な戦略から次の再帰的な方程式が得られます: \[ \mathit{LISFirst}(i) = 1 + \max \lbrace \mathit{LISFirst}(j)\ |\ j > i \text{ かつ } A[j] > A[i] \rbrace \] 自然数の集合を考えているので、\(\max \varnothing = 0\) と定義します。そうすれば「全ての \(j > i\) について \(A[j] \leq A[i]\)」ならば「\(\mathit{LISFirst}(i) = 1\)」であり、これがベースケースとなります。この再帰方程式を疑似コードで表すと、次のようになります:
procedure \(\texttt{LisFirst}\)(\(i\))
\(\mathit{best} \leftarrow 0\)
for \(j \leftarrow i + 1\) to \(n\) do
if \(A[j] > A[i]\) then
\(\mathit{best} \leftarrow \max\lbrace \mathit{best}, \textsc{LISFirst}(j) \rbrace\)
return \(1 + \mathit{best}\)
最後に、このアルゴリズムを使って元々の問題を解きます。つまり、出力配列の最初の要素を知ることなく出力を計算します。最初の要素として全ての要素を総当たりで試すというのも一つのやり方ですが、入力配列の最初に門番 \(-\infty\) を追加してその門番から始まる最長増加部分列の長さを求め、最後に \(1\) を引くという方法もあります。両方の実装を示します:
procedure \(\texttt{Lis}\)(\(A[1..n]\))
\(\mathit{best} \leftarrow 0\)
for \(i \leftarrow 1\) to \(n\) do
\(\mathit{best} \leftarrow \max \lbrace \mathit{best}, \textsc{LISFirst}(i) \rbrace\)
return \(\mathit{best}\)
procedure \(\texttt{Lis}\)(\(A[1..n]\))
\(A[0] \leftarrow -\infty\)
return \(\textsc{LISFirst}(0) - 1\)