練習問題

グラフ

次の定義が全て同値なことを示してください。
1. 木とは連結な非巡回グラフである。
2. 木とは一成分からなる森である (森は非巡回グラフ)。
3. 木とは辺が $V-1$ 個以下の連結グラフである。
4. 木とは最小連結グラフである: 任意の辺を削除するとグラフが非連結となる。
5. 木とは辺が $V-1$ 個以上の非巡回グラフである。
6. 木とは最大非巡回グラフである: 任意の二つの頂点の間に辺を追加すると閉路ができる。
$n>2$ 個の頂点を持つ任意の連結非巡回グラフには少なくとも二つの次数 $1$ の点が存在することを示してください。 "木" あるいは "葉" という単語、および木のよく知られた性質を使わずに、"連結" と "非巡回" の定義だけを使って示してください。
グラフ $(V,E)$ が二部 (bipartite) であるとは、$V$ を二つの部分集合 $L, R$ に分割して、全ての辺が $L$ の点と $R$ の点を結ぶようにできることを言います。
1. 任意の木が二部グラフであることを示してください。
2. グラフ $G$ が二部であることが、$G$ に含まれる任意の閉路の長さが偶数なことと同値であると証明してください。
3. 与えられた無向グラフが二部かどうかを判定する効率の良いアルゴリズムを説明、解析してください。
鳩が何羽か一緒になると、本能的につつき順序 (pecking order) を作ります。つまり任意の鳩の組について、必ずどちらかがもう一方をつつくことができ、相手を餌や将来のつがい相手から追い払えるということです。同じ鳩の組は何年も会っていなくても、周りにいる鳩が変わっても同じつつき順序を作ります。興味深いことに、つつき順序は全体として閉路を含むことがあります。例えば鳩 $i$ が鳩 $j$ をつつき、鳩 $j$ が鳩 $k$ をつつき、鳩 $k$ が鳩 $l$ をつついているときに、鳩 $l$ が鳩 $i$ をつつくことがあり得ます。
1. 任意の数の鳩の集まりは一列に並べて任意の鳩が前にいる鳩の背中をつつけるようにできることを示してください (鳩のパレード？)。どうかお願いします。
2. $n$ 羽の鳩のつつき関係を表す有向グラフが与えられたとします。つまりグラフの頂点が鳩を表し、鳩 $i$ が鳩 $j$ をつつくときに限って辺 $i \rightarrow j$ が存在します。(a) で存在が示されたつつき順序を計算するアルゴリズムを説明、解析してください。
3. 三羽以上の任意の鳩の集合について、(a) で示されるつつき順序は唯一であるか、そうでなければある三羽の鳩 $i,j,k$ がいて、鳩 $i$ が鳩 $j$ をつつき、鳩 $j$ が鳩 $k$ をつつき、鳩 $k$ が鳩 $i$ をつついていることを示してください。
グラフ $G$ のオイラー周遊 (Eulerian tour) とは、$G$ の閉じた歩道であって $G$ の全ての辺をちょうど一回ずつ通るものを言います。
1. 連結グラフ $G$ がオイラー周遊を持つならば $G$ の全ての頂点が偶数の次数を持つことを示してください (Euler はこれを示しました)。
2. 連結グラフ $G$ の全ての頂点が偶数の次数を持つならば $G$ はオイラー周遊を持つことを示してください (Euler はこれを示しませんでした)。
3. 与えられたグラフのオイラー周遊を計算するか、オイラー周遊が存在しなければ正しくそうだと報告するアルゴリズムを説明、解析してください (Euler がこの問題に対してぼんやりと手を振りました)。
$d$ 次元超立方体は次のように定義されます: $d$ ビットの異なる文字列でラベル付けされた頂点が $2^{d}$ 個あり、二つの頂点の間に辺があるのは対応する文字列がちょうど一文字違うときだけです。
1. ハミルトン閉路 (Hamiltonian cycle) とは $G$ の閉路であって $G$ の頂点を全て通るものを言います。全ての $d \geq 2$ に対して、$d$ 次元超立方体に Hamilton 閉路が存在することを示してください。
2. オイラー周遊 (全ての辺を一度ずつ使う閉じた歩道) を持つ超立方体はどれですか？ [ヒント: とても簡単です。]
${}$

走査アルゴリズム
有向グラフ $G$ が強連結 (strongly connected) であるとは、$G$ に含まれる任意の二つの頂点 $u, v$ に対して、$u$ から $v$ および $v$ から $u$ の路が存在することを言います。

無向グラフ $G$ が与えられ、$G$ の各辺に向きをつけて有向グラフを作るときに、出来上がるグラフを強連結にできるかどうかを判定するアルゴリズムを説明、解析してください。
$G$ を連結グラフとし、適当な頂点 $v$ を根とする深さ優先全域木を $T$ をします。$v$ を根とする幅優先全域木が $T$ と等しいならば $G=T$ であることを示してください。
Epprich 教授と Goodstein 教授は一般的な何か優先探索アルゴリズムに対する次に示す最適化を提案しました。袋から取り出した時に頂点に印が付いているかを調べる代わりに、彼らのアルゴリズムは袋に頂点を入れる時にそれを調べます。そのため各頂点は多くとも一回しか袋に入りません。このアルゴリズムでは袋に入れるときに各頂点の親も記録されます。

procedure $\texttt{EagerWFS}$($s$)

$s$ に印を付ける

袋に $s$ を入れる

while 袋が空でない do

袋から頂点を取り出して $v$ とする

for $vw$ の形をした辺 do

if $w$ に印が付いていない then

$w$ に印を付ける

$\mathit{parent}(w) \leftarrow v$

$w$ を袋に入れる
1. $\textsc{EagerWFS}(s)$ が $s$ から到達可能な頂点全てに印をつけ、それ以外の頂点には印をつけないことを示してください。同様に $\textsc{EagerWFS}(s)$ が計算する親へ向かう辺 $v \rightarrow \mathit{parent}(v)$ の集合が $s$ を含む成分の全域木を定義することを示してください。
2. キューを使って袋を実装した場合、$\textsc{EagerWFS}$ が幅優先探索と等価なことを示してください。つまり、二つのアルゴリズムが同じ頂点を同じ順番で訪れて同じ全域木を作ることを示してください。 [ヒント: キューの定義は何ですか？]
3. どんなデータ構造を袋として使っても (したがってスタックを使っても)、 $\textsc{EagerWFS}$ が絶対に深さ優先探索と等価にならないことを示してください。
  
  $\textsc{EagerWFS}$ も $\textsc{RecursiveDFS}$ も頂点 $v$ を考えているときの辺 $vw$ の順番を指定しておらず、辺の順番を変えると最終的な全域木も変わります。したがって証明のためには、具体的なグラフ $G$ に対して、$\textsc{RecursiveDFS}$ が作ることができる全ての全域木が $\textsc{EagerWFS}$ によって作られないこと (あるいはその逆) を示す必要があります。
一般的なアルゴリズムのクラスとしての何か優先探索を説明した最初期の論文の一つは、自動ガベージコレクタ研究の一環として Edsger Dijkstra (エドガー・ダイクストラ)、Leslie Lamport (レスリー・ランポート)、Alain J.Martin (アラン・J・マーティン)、Carel S. Scholten (キャレル・S・スコルテン)、Elisabeth F. M. Steffens (エリザベス F・M・ステファンズ) らによって 1975 年に発表されました。彼らのアルゴリズムでは頂点に印を付けたり消したりするのではなく、頂点に対する白、灰色、黒のどれかの色を記録します。いつも通り、アルゴリズムは固定されたグラフ $G$ を仮定します。

procedure $\texttt{ThreeColorSearch}$($s$)

全ての頂点を白く塗る

$s$ を灰色に塗る

while 灰色の頂点がある do

$\texttt{ThreeColorStep}$()

procedure $\texttt{ThreeColorStep}$()

$v \leftarrow $ 適当な灰色の頂点

if $v$ に白い隣接点が無い then

$v$ を黒く塗る

else

$w \leftarrow v$ の白い隣接点

$\mathit{parent}(w) \leftarrow v$

$w$ を灰色に塗る
1. $\textsc{ThreeColorSearch}$ の各ステップにおいて、次の不変条件が満たされることを示してください: 「任意の白い頂点に隣接する頂点は黒くない」 [ヒント: 簡単なはずです。]
2. $\textsc{ThreeColorSearch}(s)$ が停止したとき、$s$ から到達可能な全ての頂点は黒く塗られていること、到達可能でない全ての頂点は白く塗られていること、親をたどる辺 $v \rightarrow \mathit{parent}(v)$ の集合が $s$ を含む成分の根付き全域木を定義することをそれぞれ示してください。
  
  [ヒント: 直感的には黒い頂点が "印の付いた" 頂点であり、灰色の頂点が "袋に入った" 頂点を表します。しかし $\textsc{WhateverFirstSearch}$ と違って、このアルゴリズムは同じ頂点から出る辺を同じタイミングで処理しません。]
3. 次に示す $\textsc{ThreeColorSearch}$ の変種が深さ優先探索と等価であることを示してください。このアルゴリズムでは灰色の頂点の集合が通常のスタックを使って管理されます。 [ヒント: $\textsc{ThreeColorStackStep}$ の最後の二行の順番が重要です！]
  
  procedure $\texttt{ThreeColorStackSearch}$($s$)
  
  全ての頂点を白く塗る
  
  $s$ を灰色に塗る
  
  $s$ をスタックにプッシュする
  
  while 灰色の頂点がある do
  
  $\texttt{ThreeColorStackStep}$()
  
  procedure $\texttt{ThreeColorStackStep}$()
  
  スタックから頂点 $v$ をポップする
  
  if $v$ に白い隣接点が無い then
  
  $v$ を黒く塗る
  
  else
  
  $w \leftarrow v$ の白い隣接点
  
  $\mathit{parent}(w) \leftarrow v$
  
  $w$ を灰色に塗る
  
  $v$ をスタックにプッシュする
  
  $w$ をスタックにプッシュする
4. 次に示す $\textsc{ThreeColorSearch}$ の変種が幅優先探索と等価でないことを示してください。このアルゴリズムでは灰色の頂点の集合が通常のキューを使って管理されます。 [ヒント: $\textsc{ThreeColorQueueStep}$ の最後の二行の順番は重要ではありません！]
  
  procedure $\texttt{ThreeColorQueueSearch}$($s$)
  
  全ての頂点を白く塗る
  
  $s$ を灰色に塗る
  
  $s$ をキューにプッシュする
  
  while 灰色の頂点がある do
  
  $\texttt{ThreeColorQueueStep}$()
  
  procedure $\texttt{ThreeColorQueueStep}$()
  
  キューから頂点 $v$ をプルする
  
  if $v$ に白い隣接点が無い then
  
  $v$ を黒く塗る
  
  else
  
  $w \leftarrow v$ の白い隣接点
  
  $\mathit{parent}(w) \leftarrow v$
  
  $w$ を灰色に塗る
  
  $v$ をキューにプッシュする
  
  $w$ をキューにプッシュする
5. ❤ $\textsc{ThreeColorSearch}$ の実行中に他のプロセスが $G$ に辺を足していくとします。この場合、追加される辺によって (a) で示した不変条件が成り立たなくなる可能性があるので、このアルゴリズムの正しさ ――$\textsc{ThreeColorSearch}$ が終了したときに $s$ から到達可能な全ての頂点が黒く塗られていること―― が保証されなくなります。"頂点が白い" が "到達不可能だから削除しても構わない" を意味している場合、これは大問題です。
  
  しかしもし他のプロセスが辺を足すときに色についての不変条件が保たれるように気を付けるならば、他のプロセスによって辺が足されていく場合でも三色アルゴリズムを使って到達不可能な頂点を見つけることができます。二つの並列アルゴリズムを次のようにモデル化します。$\textsc{GarbageCollect}$ における either/or の選択および $\textsc{Mutate}$ における $u$ と $w$ の選択はメインのアルゴリズムから全く制御できないとしてください¹。
  
  procedure $\texttt{GarbageCollect}$($s$)
  
  全ての頂点を白く塗る
  
  $s$ を灰色に塗る
  
  while 灰色の頂点がある do
  
  $\color{red}{either}$
  
  $\quad$$\texttt{CollectStep}$()
  
  $\color{red}{or}$
  
  $\quad$ $\color{red}{\textsc{Mutate}()}$
  
  procedure $\texttt{CollectStep}$()
  
  $v \leftarrow$ 適当な灰色の頂点
  
  if $v$ に白い隣接点が無い then
  
  $v$ を黒く塗る
  
  else
  
  $w \leftarrow v$ の白い隣接点
  
  $w$ を灰色に塗る
  
  procedure $\texttt{Mutate}$()
  
  $u \leftarrow$ 任意の頂点
  
  $w \leftarrow$ 任意の頂点
  
  if $uw$ が辺でない then
  
  辺 $uw$ を加える
  
  if $u$ が黒くて $w$ が白い then
  
  $u$ を灰色に塗る
  
  if $u$ が白くて $w$ が黒い then
  
  $w$ を灰色に塗る
  
  $\textsc{GarbageCollect}$ が確かに必ず終了し、$s$ から到達可能な全ての頂点を黒く、$s$ から到達不可能な点を白く塗ることを証明してください。
6. ❤ $\textsc{Mutate}$ における不変条件を保つための処理を変更して、黒い頂点を灰色にする代わりに白い頂点を灰色にするようにしたとします:
  
  procedure $\texttt{Mutate}$()
  
  $u \leftarrow$ 任意の頂点
  
  $w \leftarrow$ 任意の頂点
  
  if $uv$ が辺でない then
  
  辺 $uw$ を加える
  
  if $u$ が黒くて $w$ が白い then
  
  $w$ を灰色に塗る
  
  if $u$ が白くて $w$ が黒い then
  
  $u$ を灰色に塗る
  
  こうした場合でも $\textsc{GarbageCollect}$ が確かに必ず終了し、$s$ から到達可能な全ての頂点を黒く、$s$ から到達不可能な点を白く塗ることを証明してください。
${}$

帰着
数迷路 (number maze) は正の整数が書かれた $n \times n$ の格子で遊ぶパズルです。駒を左上のマスに置いた状態からゲームがスタートし、ゲームのゴールは駒を左下のマスに動かすことです。ターンごとにあなたは駒を上下左右に動かすことができますが、動かせる距離は現在いるマスに書かれている整数で決まります。例えば駒が 3 と書かれているマスにある場合、動かせるのは 3 マス上、3 マス下、3 マス右、3 マス左のどれかです。ただし駒を盤の外側に動かすことはできません。

与えられた数迷路を解くために必要になる最小の手数を計算するか、パズルに答えが無ければ正しくそうだと報告する効率の良いアルゴリズムを説明、解析してください。例えば次に示す迷路に対するアルゴリズムの答えは整数 $8$ です。

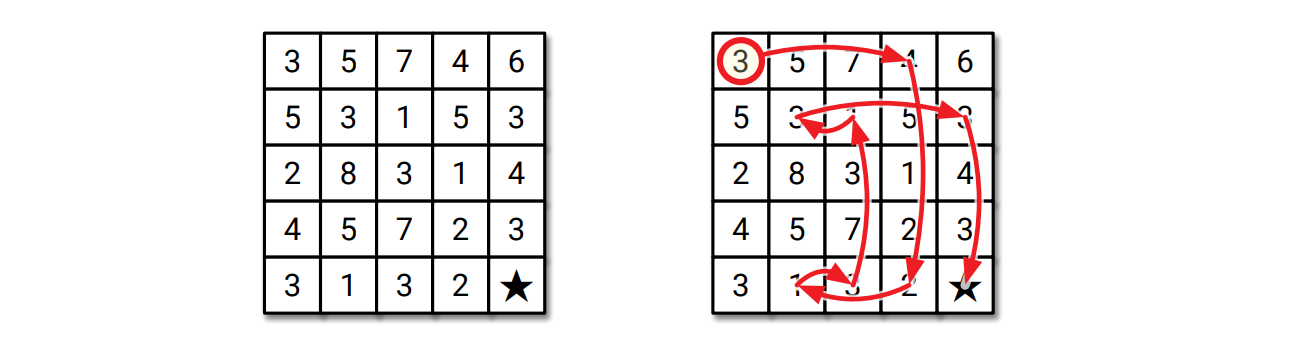$8 手で解くことができる $5 \times 5$ の数迷路$

図 5.14

8 手で解くことができる $5 \times 5$ の数迷路
蛇と梯子 (snakes and ladders) は遅くとも 16 世紀にはインドで遊ばれていた古典的なボードゲームです。盤は $n \times n$ の正方形のマスからなる格子であり、それぞれのマスには $1$ から $n^{2}$ までの数字が左下から右に向かって始まる蛇順で書かれており、行が異なる特定の二つのマスの間には「蛇 (戻る)」または「梯子 (進む)」がかかっています。一つのマスは蛇と梯子のどちらかの端点にしかなれません。

駒を左下のマス $1$ に置いた状態からゲームが始まり、各ターンであなたは駒を最大 $k$ マス進めることができます。ここで $k$ は定数です。蛇の上端に止まった駒は蛇の下端まで移動します。同様に梯子の下端に止まった駒は梯子の上端まで移動します。

盤の最後のマスに到達するまでに必要となる最小の手数を計算する効率の良いアルゴリズムを説明、解析してください。

蛇と梯子の盤 (上向きの直線の矢印が梯子、下向きの曲がった矢印が蛇を表す)
悪名高いモンゴル人パズル戦士 Vidrach Itky Leda は次のパズルを 1473 年に作成しました。パズルの盤は正の整数が書かれた正方形のマスからなる $n \times n$ の格子であり、駒は赤と青の二種類です。最初二つの駒を左上と右下のマスに置いた状態からスタートし、パズルのゴールは二つの駒の位置を反転させることです。二つの駒が同じマスに止まることはできません。

各ターンにおいて、あなたはどちらかの駒を上下左右に動かすことができ、動かすことができる距離はもう一方の駒がいるマスに書かれている数字によって決まります。例えば赤い駒が 3 と書かれているマスにいる場合、あなたが青い駒を動かすことができるのは 3 マス上、3 マス下、3 マス右、3 マス左のどれかです。ただし駒を盤の外に動かすことはできず、手の終了時に二つの駒が同じマスにいるようにもできません。

与えられた Vidrach Itky Leda パズルを解く最小の手数を計算するか、パズルに答えが無ければ正しくそうだと報告する効率の良いアルゴリズムを説明、解析してください。例えば次の図に示すパズルが与えられたとき、アルゴリズムは $5$ を返します。

$4 \times 4$ の Vidrach Itky Leda パズルに対する解
有向グラフ $G=(V,E)$ と頂点 $s, t$ が与えられたときに、$G$ における $s$ から $t$ に向かう歩道であって長さが 3 で割り切れるものが存在するかを判定するアルゴリズムを説明、解析してください (同じ辺と頂点を含んでも構いません)。

例えば次のグラフと図中 $s, t$ で示される頂点が与えられた場合、アルゴリズムの答えは $\textsc{True}$ です。なぜなら $s \rightarrow$ $w \rightarrow$ $y \rightarrow$ $x \rightarrow$ $s \rightarrow$ $w \rightarrow t$ が $s$ から $t$ への長さ 6 の歩道だからです。
辺が赤または青に塗られた有向グラフ $G$ が与えられたとします。$G$ における頂点 $s$ から頂点 $t$ への同じ色の辺が三回以上連続しない歩道の中で最短なものの長さを求めるアルゴリズムを説明してください。つまり、歩道が二回連続して赤い辺を通ったら次の辺は青い必要があり、歩道が二回連続して青い辺を通ったら次の辺は赤い必要があるということです。

例えば次のグラフが入力されたとき、アルゴリズムは $7$ を返します。なぜなら $s \color{#B52F1B}{\rightarrow}$ $a \color{#B52F1B}{\rightarrow}$ $b \color{#0071BB}{\Rightarrow}$ $d \color{#B52F1B}{\rightarrow}$ $c \color{#0071BB}{\Rightarrow}$ $a \color{#B52F1B}{\rightarrow}$ $b \color{#B52F1B}{\rightarrow}$ $t$ が $s$ から $t$ への規則を守る最短の歩道だからです。
辺が赤、白、青のどれかで塗られた有向グラフ $G$ が与えられたとします。$G$ の歩道に含まれる辺の色が赤、白、青、赤、白、青、という順番になっているとき、その歩道をフランス国旗歩道と呼びます。きちんと言うと、歩道 $v_{0} \rightarrow v_{1} \rightarrow \cdots \rightarrow v_{k}$ がフランス国旗歩道なのは、全ての整数 $i$ について、辺 $v_{i} \rightarrow v_{i+1}$ の色が $i \mod 3 = 0$ ならば赤、$i \mod 3 = 1$ ならば白、$i \mod 3 = 2$ ならば青な場合です。

与えられた頂点 $v$ からフランス国旗歩道で到達可能な $G$ の頂点を全て求めるアルゴリズムを説明してください。
$n$ 個の銀河を結ぶ $m$ 個の銀河間テレポートウェイがあります。各テレポートウェイは二つの銀河を結んでいて、双方向に使うことができ、テレポートウェイ $e$ を使うごとに $c(e)$ ドルの費用が掛かります。ここで $c(e)$ は正の整数です。テレポートウェイは複数回使っても構いませんが、使うたびに通行料がかかります。

Judy は銀河 $s$ から銀河 $t$ に行こうとしています。テレポーテーションはあまり心地良いものではないので、彼女はテレポーテーションの回数を最小にしたいと思っています。また小さな硬貨を持ち歩くのも煩わしいので、合計費用を 5 ドルの倍数にしたいとも彼女は思っています。
1. Judy が費用を 5 ドルの倍数にしつつ銀河 $s$ から銀河 $t$ に行くために必要になるテレポーテーションの最小回数を求めるアルゴリズムを説明、解析してください。
2. Judy が一度だけテレポーテーションを無料にできるクーポンを持っているとして (a) を解いてください。
Three Shea Shells は連結無向グラフ $G$ を使って遊ぶ一人用ゲームです。最初三つの駒を異なる頂点 $a, b, c$ に置いた状態からゲームがスタートします。あなたは各ターンで三つの駒全てを辺に沿って隣接する頂点に動かさなければならず、ターンの終了時には三つの駒が異なる頂点にある必要があります。このゲームのゴールは三つの駒をゴール頂点 $x, y, z$ に動かすことです。どの駒がどのゴール頂点にあっても構いません。

図 5.17

Three Sea Shells パズルの初期状態と解の最初の4手

与えられた Three Sea Shells パズルが解けるかどうかを判定するアルゴリズムを説明、解析してください。アルゴリズムへの入力はグラフ $G$, スタートの頂点 $a, b, c$, ゴールの頂点 $x, y, z$ です。アルゴリズムの出力は $\textsc{True}$ か $\textsc{False}$ の 1 ビットです。
$G$ を連結無向グラフとします。2 枚のコインを $G$ の適当な頂点においた状態から始めて、最小のステップで 2 枚のコインが同じ頂点に来るようにしたいとします。各ステップにおいて、コインは必ず隣接する頂点に移動しなくてはいけません。
1. 2 枚のコインが同じ頂点にある構成にたどり着くまでの最小ステップ数を計算するか、そのような構成が不可能ならばそうだと正しく報告するアルゴリズムを説明、解析してください。アルゴリズムの入力はグラフ $G=(V,E)$ と二つの頂点 $u, v \in V$ です ($u, v$ が同じこともあり得ます)。
2. コインが 3 枚だとします。3 枚のコインが同じ頂点にある構成にたどり着くまでの最小ステップ数を計算するか、そのような構成が不可能ならばそうだと正しく報告するアルゴリズムを説明、解析してください。
3. コインが 42 枚だとします。42 枚のコインが同じ頂点にある構成にたどり着くまでの最小ステップ数を計算するか、そのような構成が不可能ならばそうだと正しく報告するアルゴリズムを説明、解析してください。もう一度言いますが、42 枚の全てのコインがステップごとに移動する必要があります。満点のためには、アルゴリズムの実行時間が $O(V + E)$ であることが求められます。
私の娘が通う小学校で使っている算数の練習帳²には、次のタイプのパズルがいくつか載っています:

鋭角だけが含まれる線で Start と Finish をつなぎましょう。

この鋭角迷路を解くアルゴリズムを説明、解析してください。

アルゴリズムには連結無向グラフ $G$ が与えられ、頂点が平面上の点に、辺が線分に対応します。辺は端点以外の点で交わりません。例えば X の形をした迷路には 5 個の頂点と 4 個の辺が含まれ、上図左の迷路には 18 個の頂点と 21 個の辺が含まれます。アルゴリズムには二つの頂点 $\textsc{Start}$ と $\textsc{Finish}$ も与えられます。

アルゴリズムが $\textsc{True}$ を返すのは $G$ に含まれる $\textsc{Start}$ から $\textsc{Finish}$ への歩道で鋭角だけを含む物が存在するときで、それ以外の場合は $\textsc{False}$ を返します。きちんと言うと、$G$ に含まれる歩道が条件を満たすのは、歩道に含まれる任意の連続する二辺 $u \rightarrow v \rightarrow w$ について $\angle uvw = \pi$ または $\angle uvw < \pi / 2$ なときです。辺を二つ受け取ってそれらが直線か、鈍角か、鋭角かを $O(1)$ 時間で判定するサブルーチンを使えると仮定してください。
平面上の $n$ 個の垂直および水平な線分と二つの点 $s, t$ が与えられたときに、線分に触れることなく $s$ から $t$ まで移動できるかを判定する効率の良いアルゴリズムを説明してください。

水平な線分は左右の $x$ 座標と共通の $y$ 座標で与えられ、どの水平な線分も異なる $y$ 座標を持ちます。同様に垂直な線分は上下の $y$ 座標と共通の $x$ 座標で与えられ、どの垂直な線分も異なる $x$ 座標を持ちます。そして点 $s, t$ は $x, y$ 座標で与えられます。

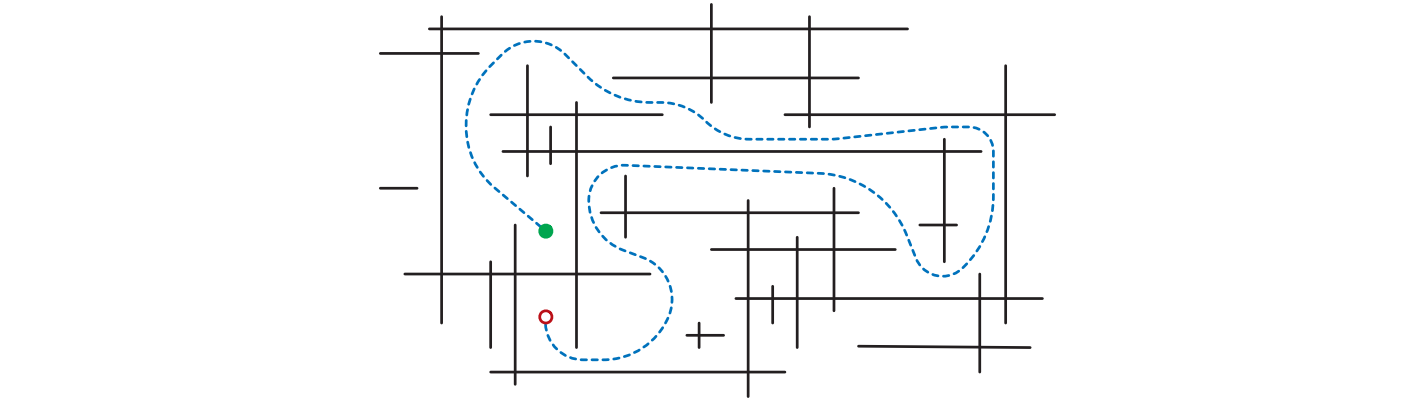図 5.18

水平および垂直な線分からなる迷路内の二点を結ぶパス
安っぽいロマンス映画にはこんなシーンがあります: 長い間引き離されていたロマンチックなカップルが突然遠くにいるお互いを見つけ、目線を離すことなくゆっくりと歩み寄り、音楽が始まり、雨はやみ、太陽が雲の間から差し込み、音楽が盛り上がり、みんなが踊り始め、虹も子猫もチョコレートのユニコーンも加わって、そして...³

ロマンチックなカップルのことを情報科学の偉大な伝統に従って Alice と Bob と呼ぶことにします。二人はお気に入りの公園に東西の入口から入ってきて、すぐにお互いを視認しました。しかし二人は一直線に近づくことができず、公園の東西の入口から延びるジグザグな歩道を通って近づかなければなりません。加えてドラマチックな緊張感を保つために、Alice と Bob が歩道を歩いている間、二人は常に東西方向の同一直線上にいなければなりません。

ジグザグな歩道の曲がり角の $x, y$ 座標が $X[0..n]$ と $Y[0..n]$ で表されていて、南西から北東に向かう方向が正方向とします。配列 $X$ は昇順にソートされていて、$Y[0] = Y[n]$ であり、歩道の曲がり角同士は直線で結ばれているとします。
1. $Y[0] = Y[n] = 0$ かつ他の全ての添え字 $i$ について $Y[i] > 0$ と仮定します。つまり、歩道の端点が他の部分よりも厳密に下にあるということです。この条件が成り立つ歩道では Alice と Bob が必ず会えるということを示してください。 [ヒント: 歩道の上を歩くカップルが存在できる場所をモデル化するグラフを作ってください。このグラフの頂点は何ですか？辺は？証明には次の握手補題を使ってください: 「任意のグラフにおいて、次数が奇数である頂点は偶数個ある」]
  
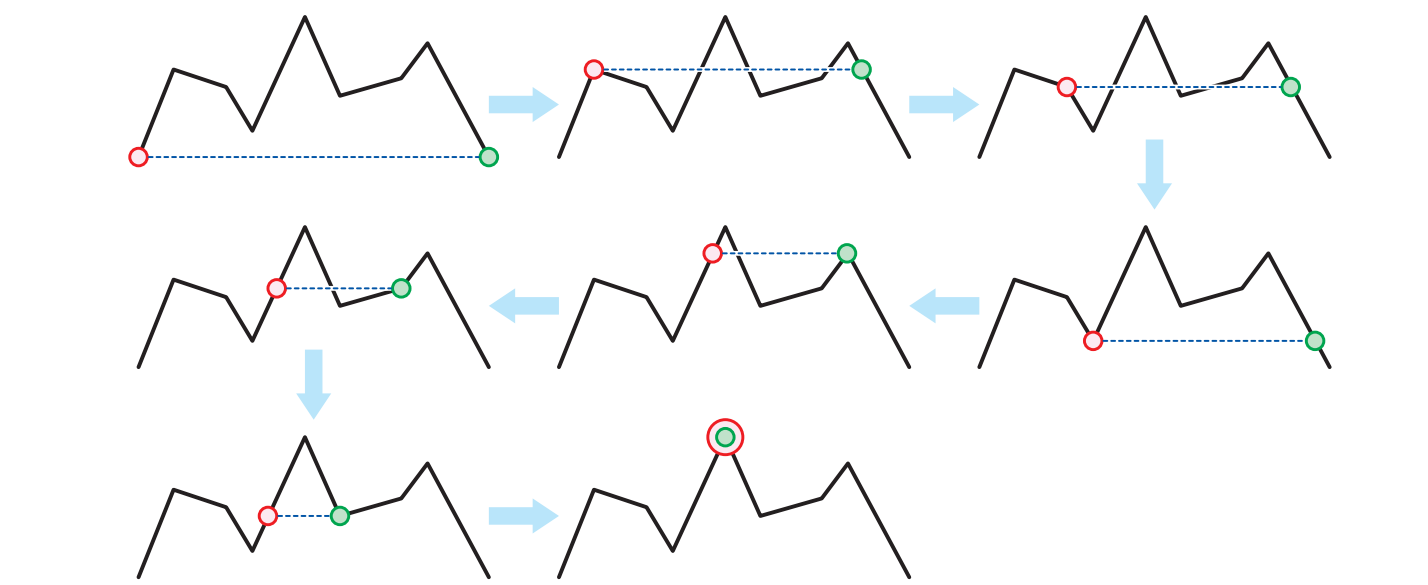  図 5.19
  
  Alice と Bob が出会う様子 (Alice はステップ 2 で後ろに下がり、Bob はステップ 5 と 6 で後ろに下がっている)
2. 歩道の端点が他の曲がり角よりも下にないときでも Alice と Bob が会えることがありますが、会えないこともあります。与えられた配列 $X[0..n]$ と $Y[0..n]$ で表される歩道において、Alice と Bob が互いに東西方向の目線を逸らすことなく、歩道の上を通って会えるかどうかを判定するアルゴリズムを説明してください。
3. ❤ (b) に対するアルゴリズムで実行時間が $O(n)$ なものを説明してください。
有名なパズル作成者 Kaniel the Dane は二つの駒と $n \times n$ の正方形のマスからなる格子を使って遊ぶ一人用ゲームを発明しました。$n^{2}$ 個のマスのうちいくつかのマスは障害物マスで、ちょうど一つのマスがゴールマスです。各ターンでプレイヤーは一つの駒を上下左右に動かしますが、そのときにはできる限り遠くまで動かします。つまり、(1) 盤の端にぶつかる (2) 障害物マスにぶつかる (3) もう一方の駒にぶつかるまで進むということです。二つの駒のどちらかをゴールマスまで移動させるのがゲームの目標です。

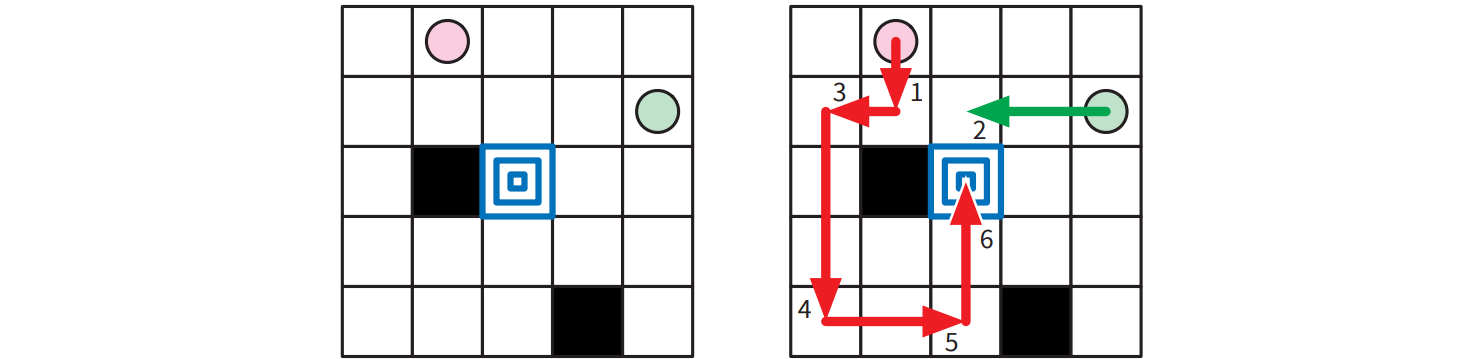図 5.20

6 手で解くことができる Kaniel the Dane のパズル (円が駒の初期位置を、黒いマスが障害物マスを、中央のマスがゴールマスを表す)

例えば、上図のパズルを解くにはまず赤い駒を下に障害物マスにぶつかるまで動かし、その次に緑色の駒を左に赤い駒にぶつかるまで動かし、その後赤い駒を左、下、右、上と動かします。緑色の駒がゴールのすぐ上にあるので、この動きによって赤い駒はゴールマスに止まり、ゲームクリアとなります。

パズルのインスタンスが解けるかどうかを判定するアルゴリズムを説明、解析してください。アルゴリズムの入力は整数 $n$ と障害物マスの座標のリストと二つの駒の初期位置です。出力は一つの真偽値です: 与えられたパズルが解を持つなら $\textsc{True}$ で、そうでないなら $\textsc{False}$ です。 [ヒント: 問題を解くグラフを構築するのに必要な時間を忘れないでください。]
❤長方形歩 (rectangle walk) は新作の抽象的パズルゲームであり、たった 99 セント購入できます。対応プラットフォームは Steam, iOS, Android, Xbox One, Playstation 5, Nintendo Wii U, Atari 2600, Palm Pilot, Commodore 64, TRS-80, Sinclair ZX-1, DEC PDP-8, PLATO, Zuse Z3, Duramesc, Odhner Arithmometer, Analytical Engine, Jacquard Loom, Horologium Mirabile Lundense, Leibniz Stepped Reckoner, Al-Jazari's Robot Band, Yan Shi's Automaton, Antikythera Mechanism, Knotted Rope, Ishango Bone, Pile of Rocks です。

このゲームは $n \times n$ の黒と白のマスからなる格子を使って遊びます。プレイヤーは次のルールに従ってこの格子の上で長方形を動かします:
- 長方形は格子とアラインされる。つまり、長方形の上下左右の座標は整数でなければならない。
- 長方形は $n \times n$ よりも小さく、かつ一つ以上のマスを含まなければならない。
- 長方形は黒いマスを含んではならない。
- プレイヤーの持っている長方形を $r$ としたときに、プレイヤーは一回の手で $r$ を $r$ に含まれる長方形または $r$ を含む長方形に変えることができる。
初期状態において、プレイヤーは盤の左上隅に大きさが $1 \times 1$ の長方形を持っています。プレイヤーの目標はなるべく少ない手で持っている長方形を右下の隅の $1 \times 1$ の長方形に変えることです。

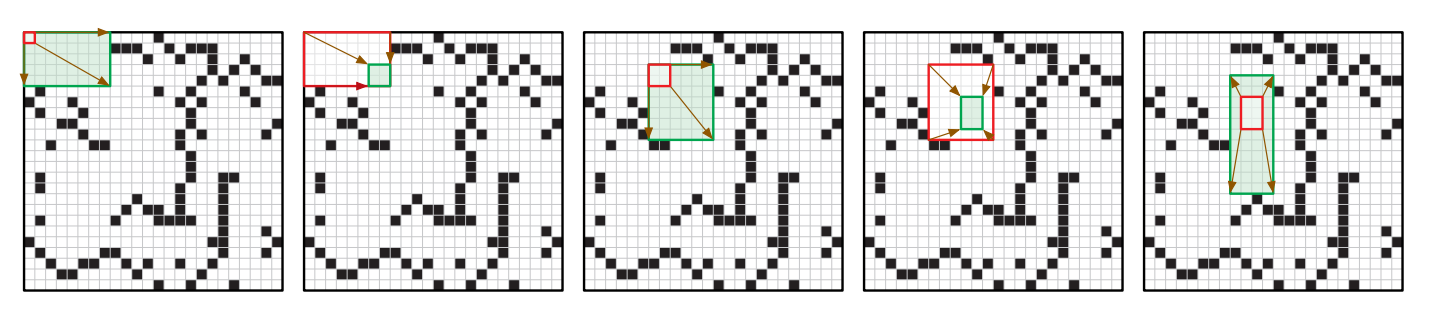図 5.21

長方形歩の最初の 5 手

与えられたビットマップにおける長方形歩の最小解の長さを計算するアルゴリズムを説明、解析してください。アルゴリズムの入力は配列 $M[1..n, 1..n]$ であり、$M[i,j] = 1$ が黒いマスを、$M[i,j] = 0$ が白いマスを表します。合法な長方形歩の存在、および $M[1,1] = M[n,n] = 0$ を仮定して構いません。例えば上図のビットマップに対するアルゴリズムの答えは整数 18 です。 [ヒント: 問題を解くグラフを構築するのにかかる時間を忘れないこと！]
Racetrack (またの名を Graph Racers, Vector Rally) は紙とペンがあれば遊べる二人対戦のゲームで、Jeff は五年生の時にスクールバスの中で遊びました⁴。このゲームでは方眼紙の上に書いたコースに沿って二人のプレイヤーが順番に車を動かします。このときのルールは以下の通りです。

方眼紙の一部にスタートエリアとフィニッシュエリアが設定されており、二人のプレイヤーはスタートエリアの好きな場所に車を置いた状態でゲームを始めます。車には $x$ 座標と $y$ 座標で表される位置 (position) と速度 (velocity) があり、ゲームの開始したときの速度は $(0,0)$ です。各ステップにおいて、プレイヤーは速度の片方または両方の成分を $1$ 増やすか減らすことができます。つまり、速度の各成分を最大 $1$ だけ変えられるということです。車の位置はこの新しい速度を現在の位置に足すことで計算されます。新しい位置はコースの内側でなければなりません。もしコースの外側に行ってしまった場合、車はクラッシュしてそのプレイヤーの負けです。どちらかの車がフィニッシュエリアのどこかについたらゲームは終了で、その車を操るプレイヤーの勝ちです。

$$25 \times 25$ の Racetrack コースに対する 16 ステップの走行 (これはこのコースに対する最小ステップの走行ではない)$

図 5.22

$25 \times 25$ の Racetrack コースに対する 16 ステップの走行 (これはこのコースに対する最小ステップの走行ではない)

Racetrack のコースが $n \times n$ のビットの配列で、0 がコースを、1 がコース外を表し、スタートエリアは最初の列、フィニッシュエリアは最後の列であるとします。与えられたコースに対して、スタートエリアからフィニッシュエリアまで行くための最小ステップ数を計算するアルゴリズムを説明、解析してください。
サイコロ転がし迷路 (rolling die maze) は通常の六面サイコロ (各面に数字の書かれた立方体) と正方形のマスからなるグリッドを使うパズルです。サイコロは必ず一つのマスの上にあり、あなたは各ステップにおいてサイコロを底面の辺に沿って 90 度回転できます。これによってサイコロは隣接する東西南北のマスのどれかに移動します。

マスの中にはブロックされたマスが存在し、サイコロはブロックされたマスの上に乗ることができません。また数字の書かれたマスもあり、サイコロがこのマスに乗るにはサイコロの一番上の数字がマスに書かれた数字と同じである必要があります。ブロックされておらず数字も書かれていないマスのことをフリーであると言います。またグリッドの外側にサイコロを転がすことはできません。サイコロ転がし迷路が解を持つとは、左下にサイコロを置いた状態からルールに従ってサイコロを転がしていってサイコロを右上のマスに乗せることができることを言います。

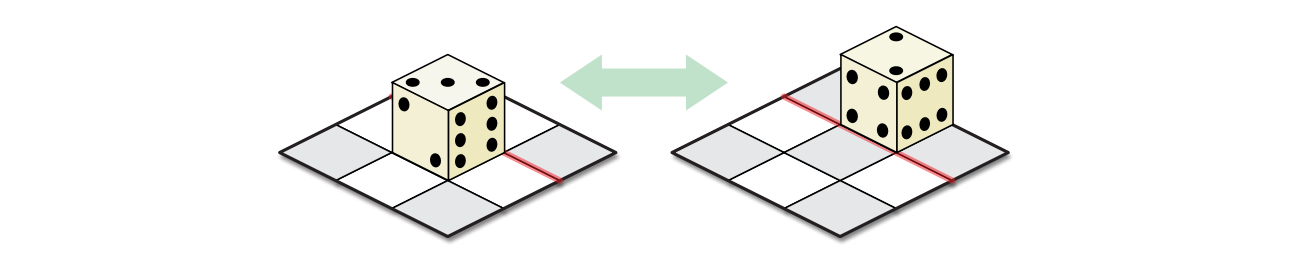図 5.23

サイコロ転がし迷路

次の図に四つのサイコロ転がし迷路を示します。1 と 6 が反対側にある標準的なサイコロを使った場合、解があるのは左の二つだけです。

図 5.24

四つのサイコロ転がし迷路 (左の二つだけが解を持つ)
1. 二次元配列 $L[1..n, 1..n]$ が与えられ、各要素 $L[i,j]$ が $i$ 行 $j$ 列のマスのラベル (0 ならフリー、-1 ならブロックされている、正の整数ならその数字が書いてある) を表しているとします。サイコロ転がし迷路が解を持つかどうかを多項式時間で判定するアルゴリズムを説明、解析してください。
2. ❤ 迷路がマスのラベルのリストで陰に定義されるとします。つまり、入力は迷路の大きさを表す整数 $M$ とマスのラベルを表す $S[i..n]$ であり、$S[i] = (x, y, L)$ が $(x, y)$ のマスのラベルが $L$ であることを表すとします。前問と同様に、マスのラベルが -1 ならばそのマスはブロックされています。ただし、フリーのマスが $S$ に含まれない点が前問と異なります。与えられたサイコロ転がし迷路が解を持つかどうかを判定するアルゴリズムを説明、解析してください。満点のためには、アルゴリズムは入力サイズ $n$ の多項式時間で実行できる必要があります。
[ヒント: サイコロの初期状態には自由度がありますが、初期状態を正しく選んだ場合にのみ解けるサイコロ転がしパズルが存在します。]
❤ 辺が赤または青に塗られた有向グラフ $G$ と二つの頂点 $s, t$ が与えられたとします。
1. $s$ から $t$ への路であって赤い辺と青い辺のパターンが回文になっているものを計算するか、そのような路が無ければそうだと正しく報告するアルゴリズムを説明してください。
2. $s$ から $t$ への赤い辺と青い辺のパターンが回文になっている路の中で最短のものを計算するか、そのような路が無ければそうだと正しく報告するアルゴリズムを説明してください。
[ヒント: 最後に回文が出てきたのはどこでしたか？ ]
♠ ❤ ドラフツ (draughts) は明るい色と暗い色で交互に塗られた $m \times m$ の格子盤⁵を使って遊ぶゲームで、米国では「チェッカー (checkers)」という名前で知られています。通常は $8 \times 8$ または $10 \times 10$ の盤を使いますが、ゲームのルールは他の大きさの盤にも簡単に一般化できます。黒いマスには (米国ではチェッカーと呼ばれる) 駒が最大一つ置かれ、白いマスには何も置かれません。駒は黒と白があります。一人のプレイヤーは白い駒を動かし、もう一方のプレイヤーは黒い駒を動かします。自分の色の駒が全て盤から取り除かれたらそのプレイヤーの負けです。

米国のチェッカー、英国のドラフツをもとにした次のゲームを考えます。このゲームでは全ての駒がキング⁶であり、四つある対角線方向の任意の方向に駒を進めることができます。各ターンで、プレイヤーは一つの駒を対角線に沿って一つ離れた空のマスに動かすか、あるいは一つの駒で連続ジャンプを行います。一回のジャンプを行うと、駒は対角線方向に二つ離れたマスに移動します。ただしジャンプが行えるのは飛び越える途中のマスに他の色の駒があるときだけです。そしてこの相手の駒は倒され、すぐにゲームから取り除かれます。一ターンで行う連続ジャンプは全て同じ駒が行わなければいけません。

白い駒のプレイヤーが一ターンで黒い駒を全て取って勝利できるかどうかを判定するアルゴリズムを説明してください。アルゴリズムの入力は盤の幅 $m$ と白い駒の位置のリスト、黒い駒の位置のリストです。満点のためには、 $n$ を全体の駒の数としたときアルゴリズムの実行時間が $O(n)$ であることが求められます。

[ヒント: 貪欲な戦術 ――何もできなくなるまで適当なジャンプを繰り返す―― は相手の駒を全て取る連続ジャンプが存在する場合にもそれを見つけられないことがあります。練習問題 5.5 を見てください。パリティ、パリティ、パリティ。]

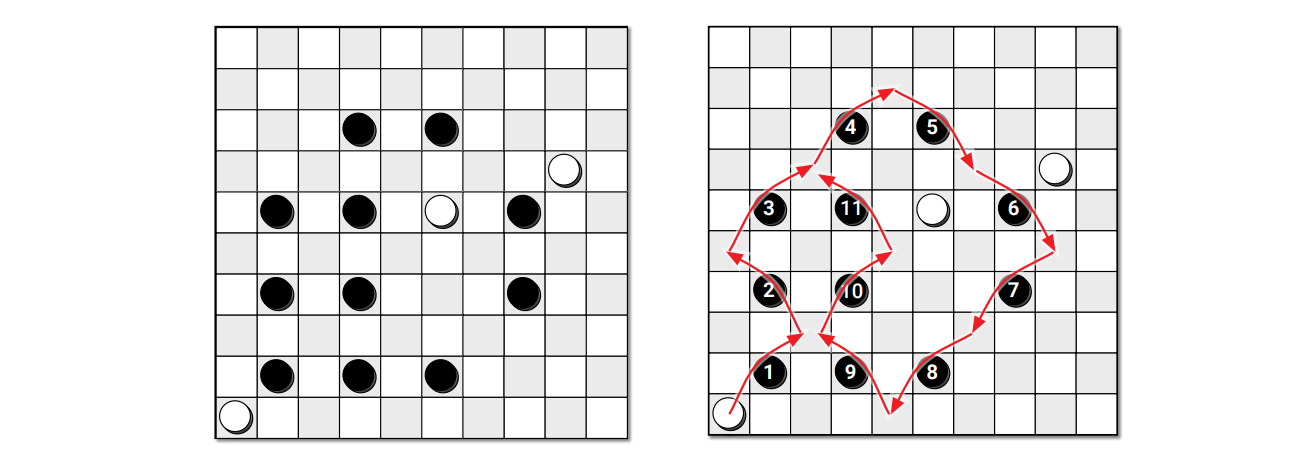図 5.25

白が一ターンで勝つ

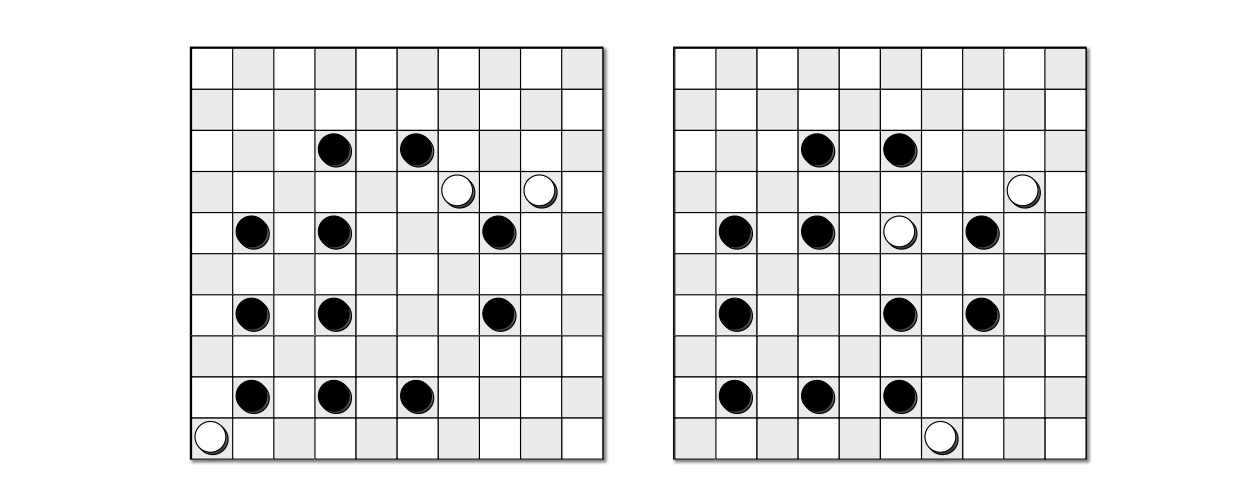図 5.26

両方の状態において、白は一ターンで勝てない

これは Lua や Go などのマルチスレッドプログラミング言語で実際に使われている "mark and sweep" ガベージコレクトアルゴリズムを大幅に単純化したものです。マルチスレッドの動的メモリ管理についてのさらに詳細な議論は残念ながらこの本の範囲を超えますが、第一の掟だけは書いておきます: 汝、自分で書いたガベージコレクタを走らせるなかれ。^[return]
Jason Batterson and Shannon Rogers, Beast Academy Math: Practice 3A, 2012. これ以外の例は https://www.beastacademy.com/resources/printables.php を参照してください。^[return]
豆知識: Whiplash と La La Land を監督した Damien Chazelle は、プリンストン大学の情報科学の教授で電子ギタリストでもある Bernard Chazelle の息子です。^[return]
実際のゲームはここに説明したものよりもう少し複雑です。素晴らしいオンラインバージョンが http://harmmade.com/vectorracer/ にあります。^[return]
中世の英国で政府会計士が計算に使っていたテーブル (counting table) は黒い正方形のチェッカー (chequer) 模様が入った緑色の布で覆われていて、その正方形の上に円形のカウンターをおいて値を表しました。このため、十世紀以降の英国では政府会計士を Exchequer と呼びます。この counting table は徴税計算の道具として Exchequer によって使われ続け、十九世紀になっても使われていました。^[return]
ドラフツの他の変種のほとんどには "空飛ぶキング" がいます。このキングは英国/米国バージョンのキングと大きく異なった振る舞いをするので、問題がとても難しくなります。この問題は12 章で見ます。^[return]