グラフへの帰着

塗りつぶし (Flood Fill)

何か優先探索の現代的な例のうち最も古いものの一つは、Edward Moore (エドガー・ムーア) によって 1950 年代中ごろに提案された、ピクセルマップに対する塗りつぶし (flood fill) 演算です。ピクセルマップ (pixel-map) とは各要素が色を表す二次元配列であり、配列の要素は picture elements (画素) を省略してピクセル (pixel) と呼ばれます1。ピクセルマップの連結領域 (connected region) とは同じ色を持つピクセルの連結な部分集合のことです。ここで二つのピクセルが連結であるとは、それらが垂直または平行に隣り合っていることを言います。塗りつぶし演算とは連結領域内の全てのピクセルの色を新しい色に変更する操作であり、多くのラスタグラフィックス編集ソフトウェアでは絵具の缶で表されています。塗りつぶし演算の入力は対象の領域に含まれるピクセルの一つを表す添え字 \(i, j\) と新しい色です。

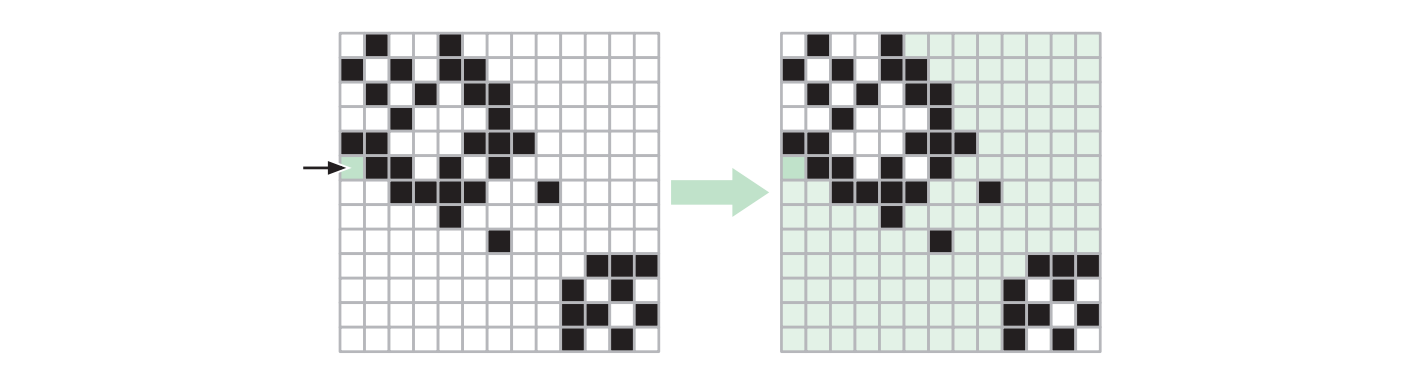
塗りつぶしの例
図 5.13
塗りつぶしの例

定義を追っていけば塗りつぶし問題を到達可能性問題に帰着させることができます: 頂点が各ピクセルに対応し、色が同じ隣り合うピクセル同士に辺があるような無向グラフを \(G=(V, E)\) とします。ピクセルマップにおける連結領域とは \(G\) における成分なので、塗りつぶし操作は \(G\) における到達可能性問題に帰着されます。この到達可能性問題は \(G\) に対する \((i, j)\) から始まる何か優先探索で解くことができます。ただし探索には少し変更が必要で、頂点に印をつけたときにその頂点の色を変えるようにする必要があります。 \(n \times n\) のピクセルマップに対するグラフ \(G\) には \(n^{2}\) 個の頂点と最大 \(2n^{2}\) の辺があるので、この何か優先探索の実行時間は \(O(V + E) = \pmb{O(n^{2})}\) です。

この単純な例には帰着の重要な要素が示されています。私たちは塗りつぶし問題を最初から解いたのではなく、知っているアルゴリズムをブラックボックスのサブルーチンとして使いました。何か優先探索が実際にどう動くかはこの問題に全く関係なく、関係があるのはその仕様、つまり何か優先探索にグラフ \(G\) と探索を始める頂点 \(s\) を入力すると、\(s\) から到達可能な全ての頂点に印が付くということだけです。ただし入力をどう構築するか、そして出力をどう使うかを説明しなければならない点は他のサブルーチンを使うときと同様です。またアルゴリズムの解析を行うときには、内部で使われるグラフアルゴリズムに対する入力ではなく元の問題への入力を使う必要があります。

ここまで来てアルゴリズムが動くようになったら ――ここで初めて――、アルゴリズムを高速化する最適化を行います。行える最適化は少なくとも二つあり、一つはプログラムによる実装に関するもので、もう一つは理論的な結論に関するものです:

  1. 1960年代に現代的なラスターディスプレイが発明されるまで、画素は「ピクセル」ではなく「スティッチ (stitche)」あるいは「テッセラ (tessera)」という名前で呼ばれていました。 "pix" という単語が "picture(s)" の短縮系になったのは 20 世紀初頭 ―― "sock" の複数系が "sox" になってから間もないころ―― であり、それまでの口語 "piccy" を置き換えました。このような単語の他の例としては voxel (volume element), texel (texture element), taxel (tactile element / badger) などがあります。[return]

広告
このページの文章はテキストゆれないくんを使って校正されました。